8-900-374-94-44
Машина Тьюринга и машина состояний, детерминированный и недетерминированный конечный автомат, конечный автомат Мура и конечный автомат Мили. Голова кругом от всех этих понятий. Как во всем этом разобраться новичку? Тем более, что и у бывалых спецов бывает такая каша в голове из этих понятий. Чего только стоит вебинар от Яндекс Практикум на тему «Конечные автоматы в реальной жизни». Именно случайный просмотр этого вебинара сподвиг меня написать статью. Я обратил внимание, что даже более опытные лекторы ловко жонглируют всеми этими понятиями или подменяют одни другими в своих лекциях. С этим можно просто смириться, или дойти до безумия, разбираясь что к чему. И как со всем этим жить начинающему ардуинщику, если про конечные автоматы в программировании трубят из каждого утюга, а добраться до истины самостоятельно непросто?
Не гарантирую, что после прочтения статьи все сразу станет на свои места, но, как минимум, постараемся выудить из всей этой «каши» что-то полезное для себя.
Так что усаживайтесь по удобнее, тема не простая, под катом будет много текста.
Да, именно так. Математика — это наука с долгой историей. Наука очень увлекательная, и поэтому она затягивает все большее количество умов. И каждому математику в душе хочется стать новым Пифагором, Евклидом, Лобачевским. А для этого необходимо постоянно расширять поле деятельности. Как только появляется какое-то новое научное направления, математики тут же жадно накидываются на него и изобретают свои новые теории.
Язык у математиков весьма своеобразный, совершенно непредназначенный для того, чтобы на нем разговаривать. Вот почему неподготовленному человеку в этих теориях сложно разобраться. К тому же, новые теории всегда строятся на уже имеющихся, происходит заимствование знакомых ранее понятий и адаптация их к новым условиям. От того путаницы становится все больше, остается ждать, пока все это как следует устоится.
Такая же участь ждала и электронику на заре ее развития.
С развитием электроники от нее стали откалываться новые направления. Одно из таких — вычислительная техника. И тут математики тоже не остались в стороне. Хорошим подспорьем стала дискретная математика, от которой перешли к математической теории вычислительной техники.
К компьютерам вычислительная техника пришла далеко не сразу. Сперва появились комбинационные логические схемы. К таким схема можно отнести знакомые всем базовые логические вентили НЕ, И, ИЛИ, Исключающее ИЛИ и другие их комбинации. Шифраторы и дешифраторы можно считать более сложным вариантом комбинационных схем.
Особенность комбинационных схем заключается в том, что значение на выходе схемы зависит только от комбинации входных сигналов в текущий момент времени.
Такие схемы не пригодны для сложных применений, так как не имеют элементов памяти. Описание работы комбинационных схем может быть выполнено в виде таблицы истинности или в виде логического выражения.
Для реализации более сложных вычислений появились последовательностные логические схемы, значения на выходе которых зависят как от текущих входных значений, так и от предыдущих. Для этого последовательностные логические схемы содержат память. Эти схемы могут явно запоминать предыдущие значения определенных входов, или могут сжимать их в меньшее количество информации, называемое состоянием системы. Состояние системы содержит всю необходимую информацию о прошлом, необходимую для определения будущего поведения схемы.
В общем случае к последовательностным схемам можно отнести все схемы, которые не являются комбинационными. То есть последовательностные логические схемы – это те, значение выхода которых нельзя однозначно определить, зная лишь текущие значения входов.
Примером последовательностных логических схем могут служить защелки или различные типы триггеров. Они способны запоминать всего один бит информации. Объединение нескольких триггеров позволяет получить более сложные схемы параллельных, параллельно-последовательных, последовательно-параллельных и прочих регистров, которые способны хранить уже несколько бит.
Поведение некоторых последовательностных схем может быть весьма сложным, для описания их работы простые таблицы истинности уже не подходят. Чтобы упростить анализ сложных последовательностных логических схем, появилась теория цифровых автоматов для построения математических моделей, использующая понятие абстрактный автомат (Abstract Machine).
Абстрактный автомат — это математическая абстрактная модель дискретного устройства, имеющего один вход и один выход, в каждый момент находится в одном состоянии из множества возможных.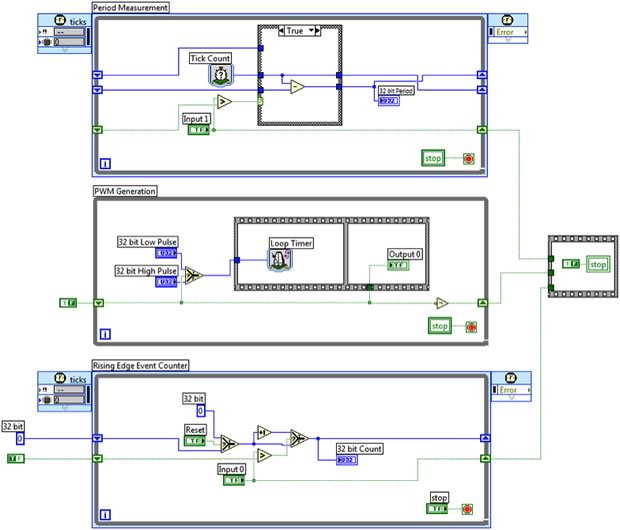
Частным случаем этой теории являются автоматы Мура и Мили, позволяющие описать функционирование цифровых систем, которые нашла широкое применение для синтеза сложных последовательностных схем на основе ПЛИС. А математические «иероглифы», которыми обильно сдобрена теория, стали хорошим подспорьем для языков описания аппаратуры подобных SystemVerilog или VHDL.
Автоматы Мура и Мили названы в честь своих изобретателей, ученых, разработавших теорию автоматов и математическую базу для них в фирме
Эдвард Форест Мур (1925–2003) опубликовал свою первую статью «Gedankenexperiments on Sequential Machines» («Мысленные эксперименты с последовательностными автоматами») в 1956 году.
Джордж Мили (1927–2010) опубликовал «Method of Synthesizing Sequential Circuits» («Метод синтеза последовательностных схем») в 1955 году. Впоследствии он написал первую операционную систему для компьютера IBM 704.
Позже он перешел на работу в Гарвардский Университет.
Схема конечного автомата содержит память для запоминания допустимых состояний. Выход схемы памяти вместе с входным сигналом поступает на входную схему формирования переходов, которая формирует новое значение в ячейке памяти (определяет следующее состояние). Также выход схемы памяти формирует выходной сигнал.
Если выходной сигнал полностью определяется значением ячейки памяти, то схему называют автомат Мура.
В ряде случаев в формировании выходного сигнала может задействоваться не только ячейка памяти, но и входной сигнал. Это позволяет сократить количество необходимых состояний. Такая схема называется автомат Мили.
Основная разница между конечными автоматами Мура и Мили в том, что у автомата Мура обычно больше (Moore – more) состояний, чем у автомата Мили, решающего ту же задачу.
Описание переходов между состояниями для автоматов удобно выражать в виде диаграмм, выполненных в виде графов.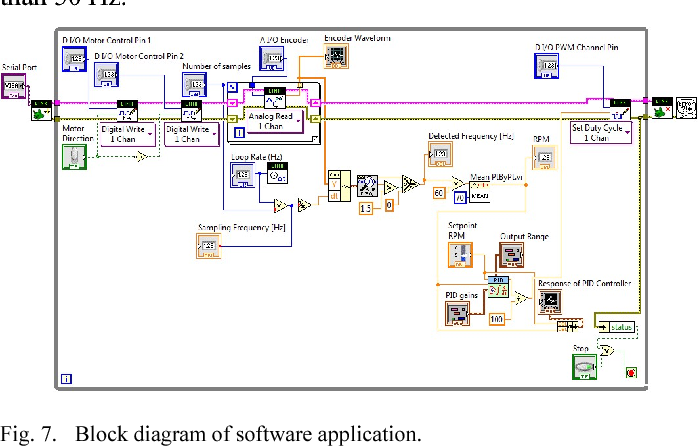
Если состояния имеют единственную последовательность переключений, то такой автомат называется детерминированным. Если из одного состояния возможно выполнить несколько переходов, то автомат называется
Цифровой автомат также может однозначно описываться таблицей переходов и таблицей выходов, которые связывают состояния ячеек памяти и входных сигналов. В каждой ячейке таблицы переходов размещаются следующие значения памяти, которые получаются под воздействием входного сигнала при текущем состоянии.
И вот, наконец вычислительная техника вплотную приблизилась к появлению компьютеров, для которых уже недостаточно было только разработать схему, но и требовалось разработать программное обеспечение. Естественно, что это потребовало новых математических теорий.
Машина Тьюринга была предложена для формализации понятия алгоритма, и является расширением или частным случаем конечного автомата.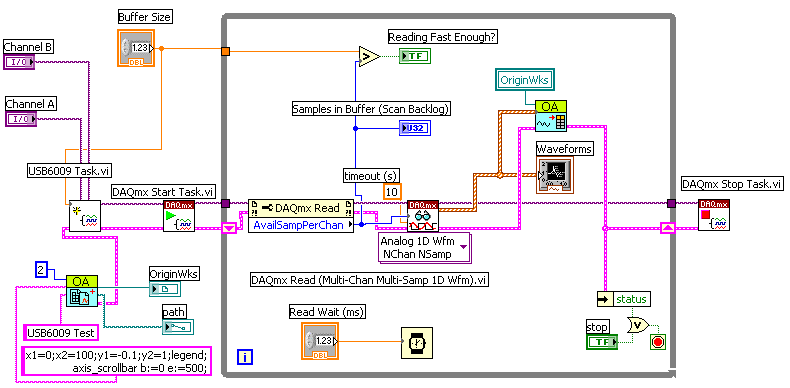
Сам Алан Тьюринг использовал понятие «вычислительная машина» («computing machine»).
Отдельно останавливаться на самом Тьюринге нет смысла, личность его достаточно известна. Чего стоит только один фильм «Игра в имитацию» с великолепным Бенедиктом Камбербэдчем. Кто не смотрел — крайне рекомендую.
Машина Тьюринга разрабатывалась для того, чтобы ответить на вопрос: «есть ли конкретный метод или механический процесс, который можно применить к математическому утверждению и он ответит, доказуемо ли это утверждение» — которым задавался известный математик Макс Ньюман на своих лекциях в Кембридже.
Нужно понимать, что математикам для работы совершенно не требовалось физически строить машину Тьюринга, а было достаточно ее формализованного описания. То есть машина существует как список правил, по которым она могла бы работать.
Кроме машины Тьюринга появлялись и другие аналогичные теории. К примеру, всего на три месяца позже независимо от машины Тьюринга вышла публикация о машине Поста.
Гениальность машины Тьюринга заключается в простой идее, что на одной и той же вычислительной машине можно реализовать совершенно разные устройства. Во многом благодаря ей в математике зародилась теория сложности вычислений.
В интернете вы можете встретить достаточное количество программных реализаций машины Тьюринга. Но, на мой взгляд, это не имеет большого прикладного смысла. К счастью, на сегодняшний день существуют другие более эффективные программные решения.
И так, мы уже увидели, как конечные автоматы используются в математике и электронике. Третье направление, где используется теория конечных автоматов — это программирование. Но не нужно думать, что используется оно в чистом виде.
Идея рассматривать программу в терминах конечного автомата сама по себе не новая.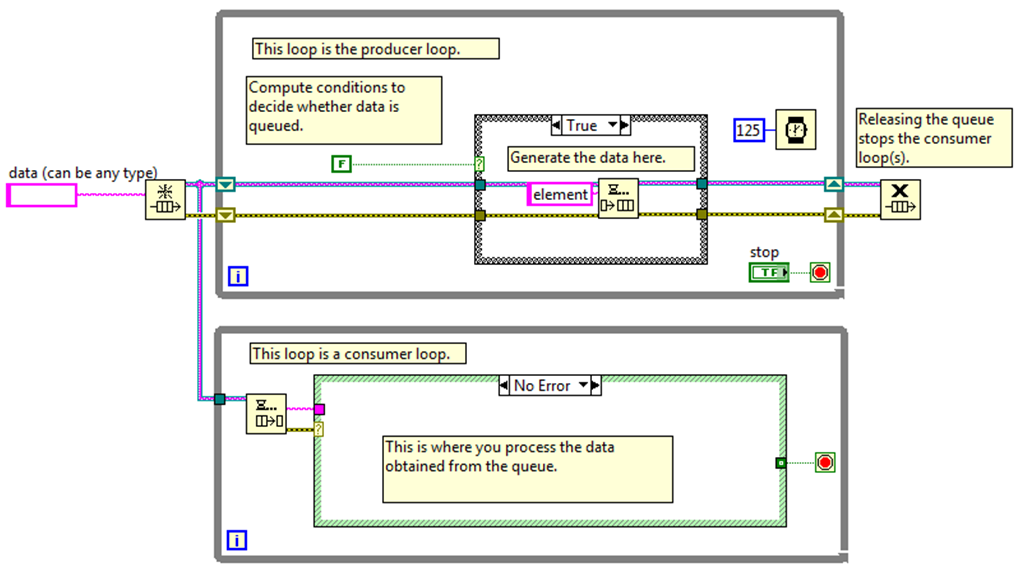
Но наиболее активно свое развитие она получила в начале 90-х годов прошлого века. Одним из основоположников данной идеи является профессор Университета ИТМО Анатолий Абрамович Шалыто. Идея заключается в том, чтобы программировать с использованием понятия «состояние». Сперва для названия этого подхода появился термин «Switch-технологии«, так как операторы множественного выбора в традиционных языках подходили для смены состояний программы больше всего. Позже, в конце 90-х термин «Switch-технологии» был заменен на «автоматное программирование«.
Теория автоматного программирования — это, прежде всего, отдельное направление в программировании, которое заимствовало некоторые термины и определения из теории автоматического управления, но при этом строится как самостоятельная теория. Для реализации автоматных программ можно использовать диаграммы Мура и таблицы состояний, но сама реализация конечного автомата в автоматном программировании будет отличаться от схемотехнической.
Автоматное программирование можно рассматривать как самостоятельную парадигму. Есть мнение, что оно должно исправить недостатки ООП, и может использоваться как дополнение к нему.
Но, так как специализированные языки для автоматного программирования еще не получили такого распространения, как традиционные языки, точно отделить автоматные программы от программ, написанных более традиционными способами, достаточно сложно. На эту тему идут постоянные споры.
Хочу заметить, что в англоязычном интернете упоминаний о работе Шалыто я не нашел. А Finite State Machine рассматривается как модель для разработки и электрических схем и программных алгоритмов. Каких-то отдельных названий для программирования конечных автоматов я тоже не встречал, обычно так и пишут: «программирование конечного автомата«. Хотя, мне лично такое название, как «автоматное программирование«, кажется удобным для обращения. На Хабре есть интересная статья, посвященная работе Анатолия Абрамовича, советую почитать.
Но, несмотря на всю неоднозначность, все же рекомендую ознакомиться с работами Шалыто, в частности с его книгой «Автоматное программирование«. В ней содержится много полезных прикладных решений. Еще есть сайт автора на эту тему.
Программирование в стиле конечных автоматов получило широкое распространение в системах автоматизированного управления, разработке компьютерных игр, текстовых интерпретаторах, все чаще используется в веб-программировании. Написано большое количество готовых библиотек, реализующих конечные автоматы, на разных языках и для разных систем программирования.
Хорошим примером языка программирования, специализированного на автоматном стиле, является язык последовательных функциональных схем SFC (Sequential Function Chart).
SFC — язык программирования стандарта IEC61131-3, предназначенный для программирования промышленных контроллеров. Широко используется в SCADA/HMI пакетах для программирования промышленных логических контроллеров PLC.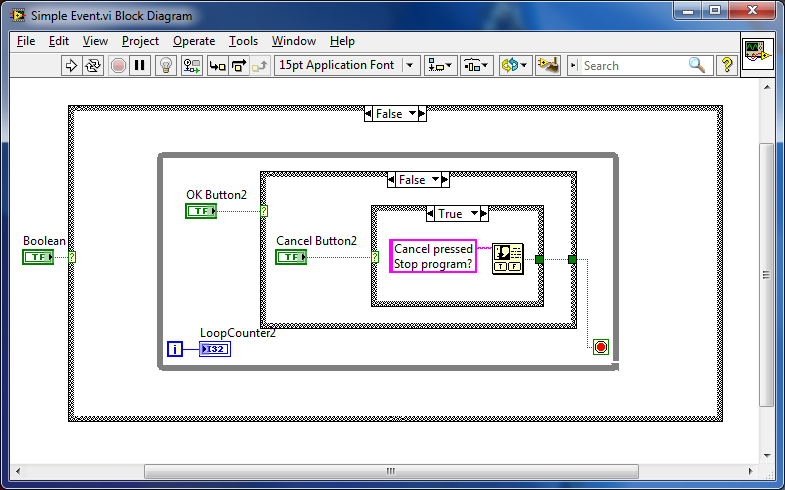
Является графическим языком, программа описывается в виде схематической последовательности шагов, объединенных переходами, подобно диаграмме состояний.
Стоит отметить, что подходы, используемые автоматным программированием, очень удобны в разработке программ для микроконтроллеров.
И все-таки, почему же с конечными автоматами получается такая каша? Мне кажется, что это связано с большим объемом знаний по данной тематике. Не все они имеют прямое отношение к программированию. Да и такая высокая формализация в программировании, как в синтезе электрических схем, скорее всего не нужна. Или все-таки нужна, но программисты обычно не уделяют этому вопросу достаточного внимания?
В общем, можно говорить о том, что такие понятия как: конечный автомат или конечный автомат состояний, и машина состояний или State Mashine, или Finite State Machine (FSM)- являются синонимами. Это связанно с особенностями терминологии на русском и английском языках.
Надеюсь, что дальнейшее изучение теории цифровых автоматов станет для вас значительно проще.
Электрокардиография представляет собой недорогой, но достаточно информативный метод кардиологического исследования. Результатом электрокардиографии является электрокардиограмма (ЭКГ) — графическое представление разности потенциалов, возникающих в результате работы сердца.
В кардиологической практике широко используется компьютерный анализ ЭКГ, основной целью которого является освобождение врача от значительной части рутинной работы. При этом можно автоматизировать распознавание особых точек и участков ЭКГ. Также поддается автоматизации этап дальнейшего анализа выделенных участков ЭКГ. Существует много алгоритмов выделения особых точек ЭКГ и методик анализа ЭКГ [1].
Постановка диагноза не может быть полностью автоматизирована, окончательный диагноз ставит врач.
Использование компьютерного анализа ЭКГ, повышает производительность врача, но и в этом случае объем информации, которую нужно проанализировать врачу для постановки диагноза остаются значительным.
Для повышения производительности врача авторским коллективом предложена система компьютерного анализа ЭКГ, в которой реализованы функции двух видов:
1. Функции выполнения аннотирования ЭКГ, назначение которых заключается в выполнении автоматического распознавания особых точек ЭКГ и присвоении каждой такой точке некоторого уникального кода.
2. Функции, реализующие расширенные возможности автоматизированного поиска характерных участков (линий) ЭКГ. Каждая линия состоит из участка ЭКГ начинающегося в аннотированной точке с заданным кодом, включая эту точку, и заканчивающегося в следующей аннотированной точке с заданным кодом, не включая эту точку.
В дальнейшем данная система будет дополняться функциями, реализующими различные методики анализа ЭКГ. Но, даже в существующем виде система значительно повышает производительность врача.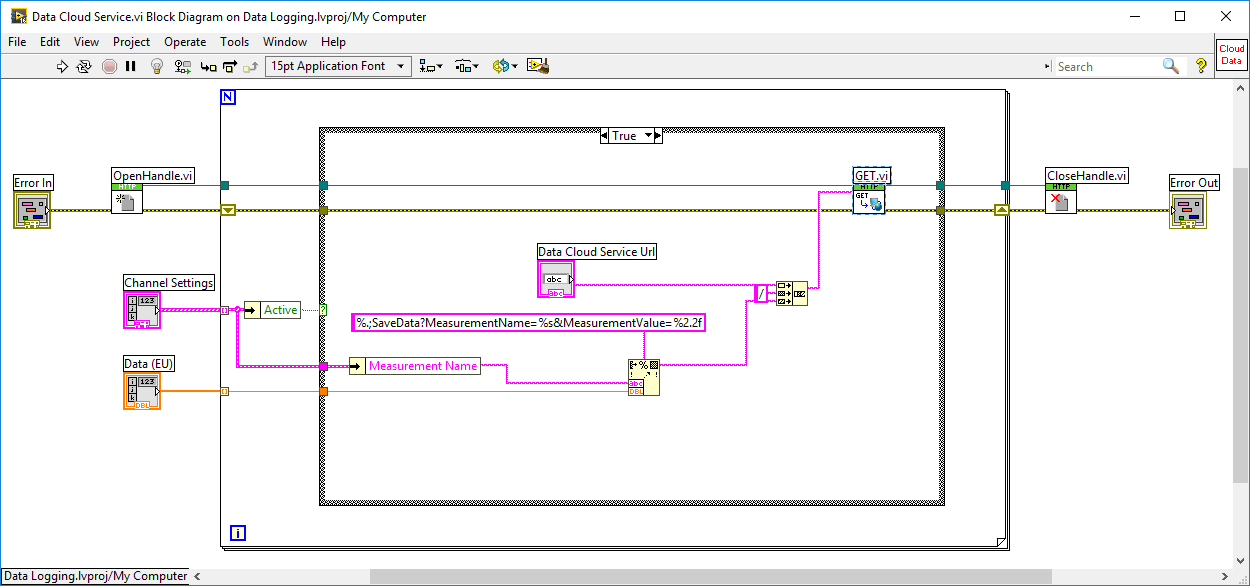
Это достигается за счет качества пользовательского интерфейса рабочего места врача, качества аннотирования и возможностей поиска произвольных линий ЭКГ.
На данном этапе реализован прототип системы, обладающий следующий функциональностью:
1. Ввод данных ЭКГ из файлов в формате банка PhysioBank [2].
2. Просмотр сигнала ЭКГ на графике с возможностью выбора и просмотра отдельных участков (окон) ЭКГ.
3. Запоминание параметров выбранных окон и передвижение по ним.
4. Автоматическое аннотирование ЭКГ.
5. Перемещение по аннотированным точкам.
6. Перемещение по зубцам R.
7. Выбор начального кода аннотации и автоматический поиск линий ЭКГ.
8. Выбор линии и перемещение по выбранным линиям ЭКГ.
Рассмотрим некоторые аспекты программной реализации системы. Реализация системы выполнена в среде LabVIEW [3]. Такой выбор обусловлен тем, что LabVIEW обладает широкими возможностями по обработке сигналов и позволяет быстро создавать приложения.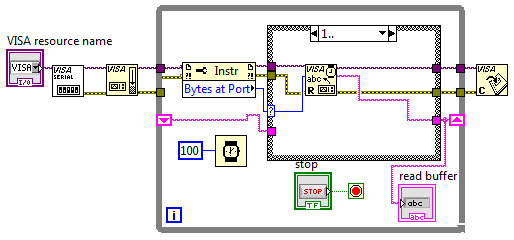
При аннотировании ЭКГ используются исходный код библиотеки, представленной в работе [4, 6].
Исходные данные программы представляются собой массив вещественных чисел D размера lenD. Элемнт массива D[i] содержит оцифрованное значение сигнала ЭКГ в i-ый момент времени (отсчет сигнала ЭКГ). Аннотация ЭКГ сохраняется в виде двух массивов AT и AS размера lenA. Элемент AT[j] содержит код аннотации присвоенный j-ой особой точке ЭКГ. Элемент AS[j] содержит номер отсчета этой особой точки.
В настоящее время система распознает 44 особых точки ЭКГ. С особыми точками ЭКГ связываются некоторые цепочки символов, раскрывающие смысловое содержание аннотации в этой точке. Каждая цепочка имеет уникальный код, поэтому можно считать, что с каждой особой точкой ЭКГ связан некоторый символ аннотации с данным кодом. Аннотации и соответствующие цепочки символов сведены в таблицу№1.
Таблица 1
Коды аннотации
Table 1
Annotations codes
№ | Цепочка | Аннотация | № | Код | Аннотация |
1. | NotQRS | Нет QRS комплекса | 23. | STCH | ST изменение |
2. | N | Нормальный ритм | 24. | PACESP | Блокада |
3. | LBBB | Блокада левой ножки пучка Гиса | 25. | T | Зубец T |
4. | RBBB | Блокада правой ножки пучка Гиса | 26. | RTM | Изменения ритма |
5. | ABERR | Ранняя предсердная экстрасистола | 27. | LEARN | Обучение |
6. | PVC | Желудочковая экстрасистола | 28. | FLWAV | Волны трепетание желудочков |
7. | FUSION | Слияние желудочкового и нормального ритма | 29. | VFON | Начало фибрилляции |
8. | NPC | Узловая экстрасистола | 30. | VFOFF | Конец фибрилляции |
9. | APC | Предсердная экстрасистола | 31. | AESC | Предсердный выскальзывающий импульс |
10. | SVPB | Преждевременная или эктопическая суправентрикулярная экстрасистола | 32. | SVESC | Суправентрикулярный выскальзывающий импульс |
11. | VESC | Желудочковый ритм | 33. | NAPC | Нет проведения зубца P |
12. | NESC | Узловой ритм | 34. | PFUSE | Переход в сунусовый ритм |
13. | PACE | Ритм | 35. | FLWAV | Волны трепетание желудочков |
14. | Q | Зубец Q | 36. | RONT | Экстрасистолия по типу R на Т |
15. | ARFCT | Изолированный QRS комплекс | 37. | (p | Начало зубца P |
16. | STCH | ST изменение | 38. | p) | Конец зубца P |
17. | TCH | Изменение волны Т | 39. | (t | Начало зубца T |
18. | SYSTOLE | Систола | 40. | t) | Конец зубца T |
19. | DIASTOLE | Диастола | 41. | ECT | Электрокардиостимулятор |
20. | MEASURE | Параметр аннотации | 42. | R | Зубец R |
21. | P | Зубец P | 43 | S | Зубец S |
22. | BBB | Левая или правая ножки пучка Гиса | 44. | RONT | Экстрасистолия по типу R на Т |
При проектировании системы широко использовались конечные автоматы. Такой подход обусловлен тем, что фактически аннотация ЭКГ представляют собой язык L=w, где w – алфавит, состоящий из 44 символов с кодами, которые могут быть присвоены особым точкам ЭКГ при выполнении автоматического аннотирования. Язык L относится к классу регулярных языков, а для формализации процессов обработки цепочек регулярного языка хорошо подходят конечные автоматы.
Проиллюстрируем использование конечных автоматов при проектировании функций, реализующих расширенные возможности автоматизированного поиска линий ЭКГ. Для хранения линий ЭКГ использовалась структура гнездового типа, представленная на рис.
1. Линии ЭКГ сохраняются в массиве LT. На начало i-ой линии указывает i-ый элемент массива uLT размера numL+1, где numL – число линий. Таким образом, i-я линия ЭКГ состоит из аннотированных точек со следующими кодами: LT[uLT[i]],…,LT[uLT[i+1]-1], а размер массива LT равен uLT[numL+1]-1.
Рис.1. Структуры данных для хранения линий ЭКГ
Fig.1. Data structures for storing ECG lines
Формирование данной структуры осуществляет конечный автомат, представленный на рис.2 в виде диаграммы состояний UML [5].
Рис.2. Диаграмма состояний конечного автомата, формирующего структуру данных для хранения линий ЭКГ
Fig.2. The state diagram of a finite automaton, forming a data structure for storing ECG lines
Код аннотации начальной точки линии хранится в переменной cl. Текущая линия сохраняется в массиве L длины lenL. Также в автомате используются функции SearchL() и AddL(). Функция SearchL() осуществляет поиск линии L в структуре LT, uLT.
Данная функция возвращает: 0 — линия аннотации не уникальна; 1 — линия аннотации уникальна и может быть добавлена в структуру LT, uLT; -1 — линия аннотации уникальна, но для ее добавления в структуру LT, uLT нет места в массиве LT; -2 — линия аннотации уникальна, но для ее добавления в структуру LT, uLT нет места в массиве uLT. Функция AddL() добавляет линию L в структуру LT, uLT. Также в автомате распознаются следующие ситуации: 0 — не найден начальный код линии аннотации; 1 — ошибок нет, линии аннотации выделены, структура LT, uLT сформирована; -3 — для массива L требуется больший размер.
На основе разработанного автомата создается функция. Все функции оформляются в виде dll. При этом используется язык Си и среда Microsoft Visual Studio. Всем возможным ситуациям нехватки памяти соответствуют уникальные коды, возвращаемые функциями. Функции вызываются из среды LabVIEW с помощью Call Library Function Node. После завершения работы функции анализируется возвращаемый код, и если возникла ошибка, связанная с нехваткой памяти, то в LabVIEW выделяется больше памяти и функция вызывается повторно.
Для демонстрационной функции pr_mem10() такая схема проиллюстрирована на рис.3. Текст функции следующий:
int pr_mem10(int* arr,int *len) {
if (*len<10) return -1;
*len=10;
for(int i=0;i<*len;i++) arr[i]=i;
return 0; }
При первом вызове функции pr_mem10() возникает ошибка, т.к. входной массив состоит из 7 элементов, а требуется 10. Перед вторым вызовом функции размер массива увеличивается на 7 и ошибка не возникает. На выход выдается массив A1=(0,1,2,3,4,5,6,7,8,9,0,0,0,0). Далее в вызывающей программе на LabVIEW из этого массива удаляются лишние элементы, и получается массив A2=(0,1,2,3,4,5,6,7,8,9).
Рис.3. Функциональной панель LabVIEW, иллюстрирующая вызов внешней функции, в которой может возникнуть ошибка нехватки памяти
Fig. 3. The functional LabVIEW panel illustrating the call of external function in which the memory error may occur
Отметим, что размеры используемых данных известны на этапе выполнения программы или хорошо предсказуемы. Поэтому ситуации, связанные с нехваткой памяти, крайне редки. Использование же статических структур позволяет повысить скорость обработки данных и отказаться от механизмов Labview Memory Manager, что в свою очередь позволяет создать независимые от LabVIEW библиотеки внешних функций.
После того как все линии ЭКГ найдены, пользователю предоставляется возможность выбрать интересующую его линию. После осуществления данного выбора формируется список начальных отсчетов выбранной линии. Эти действия осуществляет автомат представленный на рис.4. Номер выбранной линии записан в переменной nL. Список начальных отсчетов хранится в массиве LS размера lenLS. В автомате распознаются следующие ситуации: 0 — линия аннотации с номером nL не существует; 1 — ошибок нет, массив LS сформирован; -4 — для массива LS требуется больший размер. На основе данного автомата создается соответствующая функция. Реализация и вызов данной функции осуществляется аналогично функции, рассмотренной выше.
После того, как список начальных отсчетов выбранной линии сформирован, пользователю предоставляется возможность перемещаться по данным отсчетам с целью поиска характерных участков ЭКГ и их анализа.
Рис.4. Диаграмма состояний конечного автомата, формирующего список начальных отсчетов выбранной линии
Fig. 4. The state diagram of a finite automaton, generating a list of initial samples of a selected line
Итак, мы рассмотрели два автомата, которые служат для организации поиска и просмотра линий ЭКГ. Данные автоматы использовались при проектировании средств автоматизированного поиска характерных участков ЭКГ. В рассматриваемой системе конечные автоматы также применялись при проектировании других функций, например, расчета изолинии ЭКГ, преобразования форматов исходных данных и др. Использование конечных автоматов при проектировании системы позволило наглядно представить логику работы системы, избежать ошибок проектирования и в целом ускорить процесс создания системы.
Анализ результатов тестирования прототипа системы компьютерного анализа ЭКГ с расширенными возможностями автоматизированного поиска характерных участков позволяет сделать вывод о том, что достоверность расшифровки ЭКГ врачём-кардиологом с целью постановки диагноза повышается при существенном сокращении времени на выполнение этой процедуры. Это достигается за счет хороших результатов автоматического распознавания особых точек ЭКГ и автоматизированных средств поиска линий ЭКГ.
Обратитесь к учебному пособию Modify the Simple State Machine LabVIEW Template, чтобы узнать, как начать работу с ним.
Прежде чем настраивать шаблон, задайте себе следующие вопросы:
Существуют различные методы определения следующего состояния для перехода, которые обсуждаются ниже.
Обратите внимание, что хотя в примерах изображений показано состояние «Init», эти возможности перехода могут применяться к любому состоянию.
Один к одному: Если вы всегда переходите из состояния A в состояние B, нет необходимости программировать какую-либо логику, просто выведите имя следующего случая (Case B) в сдвиговый регистр.
Рисунок 3a: Только одно возможное состояние перехода для оценки состояния индикатора. Вы должны оценить что-то, что определяет, в какое состояние вы хотите перейти. Например, на рисунке 3b мы видим, что пользовательский ввод кнопки «Стоп» определяет, переходим ли мы из состояния включения питания или переходим к выключению.
Рисунок 3b: Два возможных состояния перехода константа для программирования перехода. Например, на рисунке 3c выполняется некоторый код, где результат кода определяет переход, выходом которого является массив логических значений. Логический массив коррелирует с константой Enum, которая содержит список возможных состояний, в которые можно перейти. Используя функцию Index Array, выводится индекс первого «Истинного» логического значения в логическом массиве. Затем, используя функцию Array Subset, вы можете вытащить соответствующее значение из константы Enum, с которой оно коррелирует. 9Рисунок 3c
Чтобы сопоставить логический массив с константой Enum, используйте функцию приращения, чтобы исправить это смещение.
Один к нескольким с использованием цикла While: Другой вариант, если у вас есть несколько возможных переходных состояний, — использовать цикл while внутри кейса. Код внутри цикла while будет выполняться до тех пор, пока логический статус не будет установлен в значение true, что приведет к срабатыванию кнопки остановки. Это позволит эффективно выполнять код до тех пор, пока не произойдет инициирующее событие.
На рисунке 3d показано состояние «Init», использующее внутренний цикл и структуру case для перехода к следующему состоянию. Внутренняя структура case содержит одну диаграмму для каждого перехода, который покидает текущее состояние. Каждый из вариантов во внутренней структуре case имеет два выхода: логическое значение, указывающее, следует ли выполнять переход, и перечисляемая константа, указывающая состояние, в которое переходит переход. Используя индекс цикла в качестве входных данных для структуры case, этот код эффективно проходит каждый случай перехода один за другим, пока не найдет диаграмму с «истинным» логическим выводом. После того, как будет найден «истинный» логический вывод, кейс выводит новое состояние, в которое переходит переход. Хотя этот метод может показаться немного более сложным, чем предыдущие методы, он предлагает возможность добавлять имена к переходам путем «приведения» вывода индекса цикла к перечисляемому типу. Это преимущество позволяет добавить «автоматическую документацию» в код перехода. 9Рис. 3d
Использование перечисления
Проблема : перечисления широко используются в качестве селекторов регистра в конечных автоматах. Если пользователь попытается добавить или удалить состояние из этого перечисления, оставшиеся провода, подключенные к копиям этого перечисления, разорвутся. Это одно из наиболее распространенных препятствий при реализации конечных автоматов с перечислениями.
Решение : Возможны два решения этой проблемы:
1. Если скопировать все перечисления из измененного перечисления, разрывы исчезнут.
2. Создайте новый элемент управления с перечислением и выберите «typedef» в подменю. При выборе typedef все копии перечисления будут автоматически обновляться, если пользователь добавляет или удаляет состояние.
Из LabVIEW Wiki
(Перенаправлено из конечного автомата)
Перейти к: навигация, поиск
Содержание
|
Конечный автомат — один из фундаментальных шаблонов проектирования в LabVIEW. Конечные автоматы используются для реализации сложных алгоритмов принятия решений, представленных диаграммами состояний или блок-схемами. Конечные автоматы используются в приложениях, где существуют различимые состояния. Каждое состояние может привести к одному или нескольким состояниям, а также может завершить поток процесса.
Конечный автомат состоит из структуры case, содержащейся в цикле while. Первое выполняемое состояние определяется вводом в селектор вариантов. Пользовательский ввод или расчеты в состоянии определяют, в какое состояние перейти дальше. Переход к следующему состоянию для выполнения управляется с помощью регистра сдвига. Путем подключения вывода из одного корпуса к следующему (подключение к регистру сдвига с правой стороны) и подключения входа к селектору случаев из регистра сдвига с левой стороны можно упорядочить операции в соответствии с тем, какое состояние выполняется.
Преимущество конечного автомата в том, что он позволяет последовательно связать несколько шагов, чтобы каждый отдельный шаг можно было легко выполнить (или отладить). Ловушка для неопытного программиста заключается в использовании конечного автомата для бессистемного прохождения вариантов в цикле. Это может привести к сложным путям через конечный автомат, напоминающим запутанные операторы goto в обычных текстовых языках. Однако конечные автоматы являются ценным инструментом и могут быть очень эффективно использованы с учетом этого.
Конечные автоматы могут быть основаны на целых числах, строках или перечисляемых типах. Относительные достоинства каждого подробно обсуждались в другом месте. Таким образом, конечный автомат перечисляемого типа имеет то преимущество, что автоматически обновляется при изменении перечисления (если перечисление является определением типа), но имеет недостаток, заключающийся в необходимости тщательной проверки всего кода, если добавляются новые состояния (перечисления) или они избыточны. состояния удалены. Преимущество строкового конечного автомата состоит в том, что состояния легко добавляются или удаляются, но недостатком являются орфографические ошибки, вызывающие ошибки программирования (Примечание: это можно уменьшить, включив состояние «По умолчанию», показывающее случай с ошибкой во всплывающем диалоговом окне, как видно ниже).
Существует три возможных способа заказа конечного автомата LabVIEW. Первый и самый простой способ (хотя НЕ рекомендуется) — использовать целое число. Целочисленный вывод из одного случая подключается как селектор для следующего случая. Недостатком этого метода является то, что сами по себе числа не очень помогают в отслеживании кода, а селектор регистра становится несколько бессмысленным. Любой из следующих методов является предпочтительным, и у каждого из них есть свои плюсы и минусы. Дебаты (иногда острые) довольно часто возникают в отношении списка лучших из этих методов, но на практике любой из них будет работать очень хорошо.
Второй метод заключается в использовании строки в качестве селектора регистра. При правильном выборе строковых состояний это имеет то преимущество, что каждый случай помечается так, что ваш конечный автомат становится самодокументируемым. Еще одним преимуществом этого метода является то, что все случаи не нужно записывать в первом экземпляре, и несколько проще включать новые состояния, если возникнет такая необходимость (особенно в более ранних версиях LabVIEW (< 6.0)). Недостатком является то, что легко ошибиться в написании состояния, и из-за него конечный автомат будет глючить. Простой способ преодолеть этот недостаток — включить кейс по умолчанию, который выводит предупреждение, включая написание неудачного кейса.
Третий метод заключается в использовании перечисляемого типа в качестве селектора регистра. Предпочтительно это перечисление должно быть определением типа, чтобы изменения в состояниях отражались легко и прозрачно при добавлении новых состояний в перечисление (посредством автоматического обновления LabVIEW из настройки определения типа). Обратите внимание, что есть отчеты, в которых этот метод вызывает проблемы в версии LabVIEW до 6.0, потому что автоматическое обновление перечисления неправильно обрабатывало вновь вставленные случаи. Этот метод имеет преимущество строкового метода в документации по коду, но требует использования регистра по умолчанию, если не все случаи требуется записывать при первом создании кода.
Данные обычно передаются между состояниями конечного автомата с помощью регистра сдвига, подобно тому, как переменная состояния передается между состояниями. Общепринятой практикой является использование одного кластера (предпочтительно определения типа) для хранения всех данных в одном регистре сдвига, а не нескольких регистров сдвига для нескольких элементов данных.
Шаблон секвенсора представляет собой разновидность конечного автомата. Вместо состояния, ведущего к одному или нескольким состояниям, состояния секвенсора жестко запрограммированы в массиве, который определяет порядок выполнения. Только состояние, вызывающее ошибку, изменяет последовательность операций, останавливая конечный автомат. Состояние можно выполнить более одного раза, включив его в несколько мест жестко закодированного массива состояний. Подробнее о паттерне секвенсора см.
Шаблон сценария VI представляет собой вариант конструкции конечного автомата, специально предназначенный для написания кода сценариев VI. Он использует перечисление в качестве определения последовательности событий, в которой нужно проходить, увеличивая перечисление для каждого состояния. Поэтому последовательность выполнения состояний жестко закодирована. Шаблон сценария VI не будет повторять состояние из-за того, что перечисление не может иметь две записи с одинаковым именем, если для одного и того же состояния не используются два значения перечисления. Ошибка, возникающая в любом состоянии, приведет к завершению конечного автомата. См. дополнительные сведения о шаблоне сценариев VI.
Последовательность Natt — это мини-шаблон, используемый для последовательного выполнения кода LabVIEW. Он имеет множество преимуществ по сравнению с другими конструкциями последовательного кода (такими как плоская последовательность, составная последовательность или цикл последовательности), в том числе:
Шаблон VI Natt Sequence и поддерживающий его VIM можно использовать в LabVIEW 2017 SP1 и более поздних версиях. Узнайте больше о последовательности Натта
Еще не все
