8-900-374-94-44
ПИД-регулятор является простейшим регулятором, имеющим эффективные аппаратные аналоговые реализации, и потому применяемый наиболее широко. Для своей работы требует настройки 3х коэффициентов под конкретный объект, позволяющие подобрать процесс регулирования согласно требованиям. Обладая простым физическим смыслом и простой математической записью, применяется широко и часто в регуляторах температуры, регуляторах расхода газа и других системах, где требуется поддерживать некий параметр на заданном уровне, с возможными переходами между разными заданными уровнями. Разумеется, существуют более сложные регуляторы, позволяющие более точно и быстро и с меньшими перерегулированиями выходить на заданные параметры, а так же учитывающие нелинейность или гистерезис регулируемого объекта, однако они обладают большей вычислительной сложностью и сложнее в настройке.
Несмотря на свою простоту как физического смысла, так и математической записи:
Причем проверить качество реализации ПИД регулятора крайне легко.
Рассмотрим простейший пример: терморегулятор. Для проверки его качестве лучше всего подходит быстрый, малоинерциальный, маломощный объект. Классика жанра: обычная лампочка на 100Вт с прикрученной к ней тонкой термопарой (ХА). И первое, на чем следует проверять ПИД регулятор — деградация ПИД до просто П-регулятора. То есть коэффициенты интегральной и дифференциальной ставим в ноль, а пропорциональную ставим в максимум.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит. Начинаем начинаем увеличивать уставку: 16.1, 16.3, 16.7, 18… 19… лампочка загорелась. Как?! Откуда?! Останавливаемся — выключилась. Итак, мы встретились с первой классической ошибкой реализации ПИД регулятора.
Небольшое математическое отступление: вспомним еще раз интегральную запись указанную выше. Мы реализуем её програмно, а значит — дискретно. То есть с завидной регулярностью производим измерение входной величины, сравниваем её с уставкой, вычисляем воздействие, выдаём, повторить.
А значит, надо из интегральной формы перейти в конечно-разностную схему. При переходе обычно используется переход «в лоб»:E(n) = X(n) - X0(n) — то есть величина рассогласования между текущим и заданным значением регулируемого параметра.Использование прямой формулы потребует во-1х считать и хранить интеграл рассогласований за большой период, во-2х требует работы с плавающей точкой высокой точности (так как интегральный коэффициент Ki всегда < 1), либо операции деления (представляя коэффициент в форме 1/Ki) большой разрядности. Всё это требует вычислительных ресурсов, коих в embedded как правило сильно ограничено… Поэтому, вместо реализации прямой схемы, реализуют рекуррентную формулу:
Итак, вернёмся к нашему регулятору. Итак, есть регулируемый объект: лампочка. Для управления подаваемой на неё мощностью, используют простой подход: сеть питания (220В 50Гц) подаётся через симистор на нагрузку.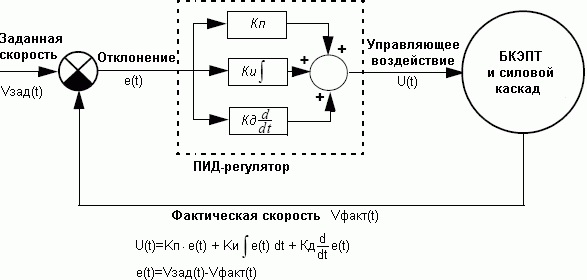
Симистор в момент перехода полуволны через ноль выключается, и остаётся выключен до тех пор, пока не будет подан сигнал на управляющий электрод. Таким образом, чем раньше после начала полуволны мы подадим управляющий сигнал, тем больше энергии от этой полуволны достигнет управляемого объекта. Правильно расчитав время для линейности площади части полуволны с момента времени X до конца полуволны, мы получаем возможность выдавать мощность от 0 до 100% с точностью, с которой расчитали таблицу линеаризации.
Итак, мы можем выдавать мощность от 0 до 100%. В реальных объектах, часто нельзя выдавать 100% мощности — например, это черевато перегоранием нагревательного элемента. Поэтому, все приборы имеют настройку минимальной и максимальной выдаваемой мощности на объект.
Итак, после вычисления U(n) по вышестоящей формуле, добавляется еще ограничение результата:if Un < Umin then Un := Umin; if Un>Umax then Un := Umax;
После чего, вычисленное Un и есть требуемая выходная мощность на текущий момент.
Та-дам! Именно вот эта реализация и создаёт ошибку, о которой написано выше.
Причина банальна: в момент перехода от дикретной к конечно-разностной схеме, мы «выносим за скобки» операцию вычисления интеграла, и на каждом шаге мы прибавляем производную к накопленной сумме
Вывод №1: вычисление U(n) нельзя ограничивать. Для ограничения мощности подаваемой на выходное устройство следует заводить отдельную переменную.
Теперь, когда мы завели Urn, для ограниченной мощности, перезаливаем, продолжаем тестировать.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит.
Пока ждём и медленно осознаём, что мы явно напоролись на какой-то «Классический Косяк №2» ™ лампочка медленно разгорается, выходит на 100% мощности, и так и остаётся — 600-то градусов она выдать ну никак не может.
Возвращаемся снова к нашей разностной схеме. U(n) = U(n-1) + Kp*(dE + ...). К текущему расчетному значению воздействия прибавляется разность невязки помноженная на коэффициент пропорциональности. У нас была уставка 60, температура 60, то есть невязка нулевая.
Выходная мощность так же была нулевая. И тут разом, скачком, уставку увеличили до 600 градусов. невязка резко стала 540 градусов, помножили еще и на коэффициент пропорциональности… и вылетели за разрядность хранения U(n). Не смейтесь, использование математики с фиксированной точки, вместо плавающей точки. При разнице в 540 градусов и работе через 1/16, при коэффициенте пропорциональности 20, получаем… 540*20*16=172800, а если у нас 16тиразрядный U(n), да еще и знаковый, то фактически, в результате вычисления мы получили A300h = −8960. Опачки. Вместо большого плюса — ощутимый такой минус.
Вывод №2: вычисления должны проводиться с корректной поддержкой переполнения. Переполнилось? Ограничь предельным числом, уж никак не заворачивать.
Итак, нарастили разрядность U(n), перетранслировали, зашили, запускаем. Лампочка еще не совсем остыла, там 80 градусов, уставка всё те же 600. Лампочка зажигается… и тухнет. Зажигается и тухнет. Как так? Уставка 600, лампочка 80 — и поддерживает вполне себе свои 80! Как так-то?! Явно у нас вылез Жучок №3.
И снова лирически-математическое отступление. Итак, есть наша разностная схема: U(n) = G(U(n-1), dE(n)). Еще раз: новое значение воздействия есть сумма прошлого воздействия и некого воздействия, зависящего от разности невязки в текущий момент и предыдущий. А что такое предыдущий момент? А какой момент предыдущий у предыдущего? Ну-ка, вспомнили школу. Доказательство по индукции. Если можно построить доказательство для K+1, считая что доказательство для K верно, И доказать отдельно что верно для K=0, тогда доказательство истинно. Итак, а как мы считаем U(0)?
Часто встречающееся решение: всё обнуляем, уставку считываем из флешпамяи уставки, ждём 1 цикл опроса, и считываем X(0). Вот, ноль готов, теперь работаем. И… И не правильно. Почему? Потому что рекурентная формула отталкивается от изменений в невязке. А проинициализировав нулём и загрузив текущие значения мы потеряли стартовые условия. Всё — вместо поддержания абсолютного значения температуры на уровне равном абсолютной уставке регулятор начинает держать температуру равную стартовой плюс разнице уставки.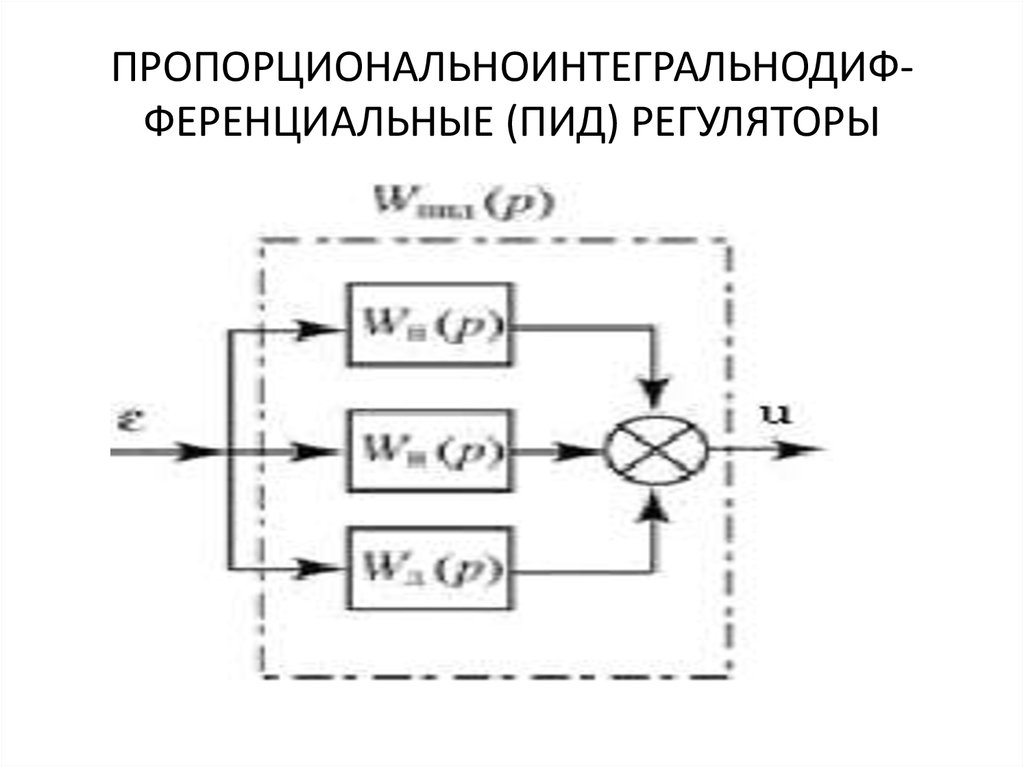
Правильная инициализация разностной схемы: обнулить _вообще всё_. То есть X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
И на первом же цикле вычислений у нас как бы скачком появляются уставке и текущее значение:X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 - 80 - 0) = 2400
Вот теперь схема работает правильно.
Вывод №3: корректно инициализируй стартовые условия.
Правильно ли? Hу-ка, ну-ка… Еще раз… Ставим уставку 20. Ждём охлаждения… Выключаем. Включаем. Итак, красота: текущая 20, уставка 20. Ставим скачком 600. Поехало греться. 100, 120… ставим уставку 20. Отключилось, пошло охлаждаться. Ждём чуток (120… 110… 100… 90… 80…) и ставим уставку 100. Поехало греться… 105 градусов, отключилось. Стоп. А почему оно держит 105? У нас же сейчас работает только пропорциональная составляющая.
При правильной реализации из физического смысла процесса колебательный процесс не может держать уставку выше чем задано. Строго ниже. А держит на 5 градусов больше чем попросили. Это наблюдается Прикол №4.
Итак, вспоминаем что у нас было выше: Вывод№2: U(n) нельзя ограничивать. И Вывод№3: при переполнении ограничить всё-таки придётся. Да-да. Иначе «рабочая точка» смещается на ограниченный момент. Что же делать? Увеличить разрядость? Хорошо, если хватает вычислительной мощности. А надо ли? Собственно, что плохого, что у нас U(n) = 9999.99, а не 29999.99? В общем-то только то, что мы потеряли 20000. Но сейчас-то для работы нам так и так надо вваливать просто 100% мощности, правильно? Правильно. Значит, проблемы с ограничением в полку нет, до тех пор, пока мы не отходим от предела. Таким образом, в случае переполнения надо ставить флаг, и по достижении, например, половины диапазона (то есть как U(n) после 9999.9 опустилось ниже 5000.00), заново реинициализировать схему. То есть отбрасывать историю, сказать что n=0 и см.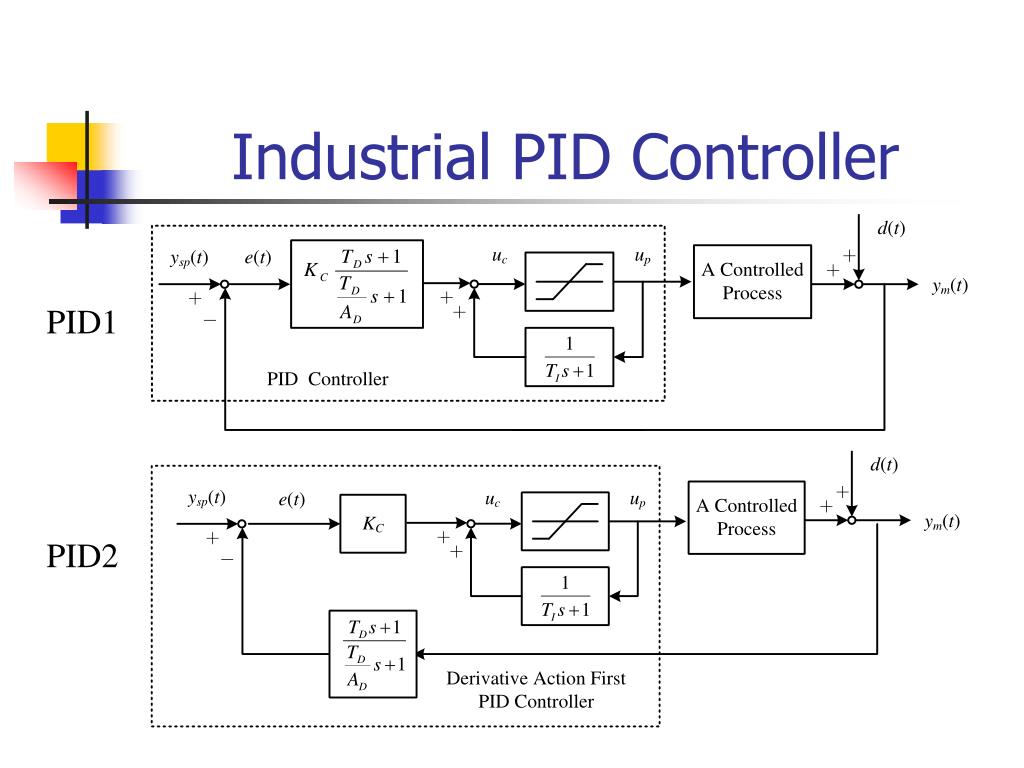
Вывод №4: если по какой-то причине U(n) было ограничено, схему следует переинициализировать как только создалось впечатление, что схема вернулась в нормальное состояние.
В следующем выпуске: а так ли надо реализовывать разностную схему? Подробная реализация прямой дискретной схемы, обладающей простыми и понятными настраиваемыми коэффициентами, с прямым физическим смыслом, которая без проблем вычисляет управляющее воздействие с частотой 25Гц на процессоре ADuC847 (быстрый 8-битный контроллер, с ядром 8051), оставляя еще море процессорного времени для других процессов.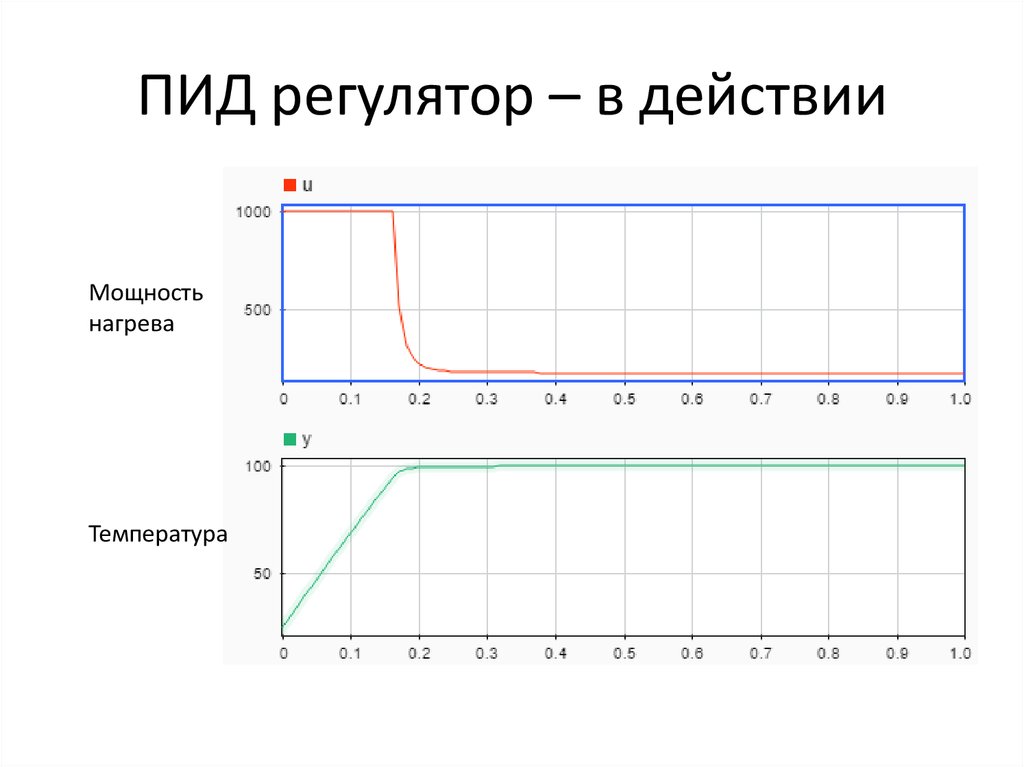
(Картинки с изображением формул взяты из статьи ПИД-Регулятор в Wikipedia)
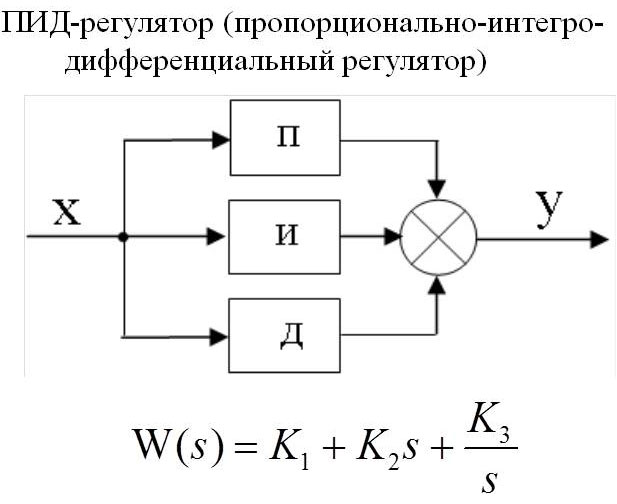
ПИД-регулятор — это прибор для управления технологическим процессом, который используется в методе ПИД-регулирования, основанном на трех законах регулирования: пропорциональном, интегральном и дифференциальном.
ПИД-регуляторОбратите внимание на теорию автоматического регулирования и на приборы для регулирования.
Интегральный сильфон и переменное ограничение позволяет обеспечить интегральное регулирование. Два дифференциальных сильфона и другое переменное ограничение дает возможность регулятору осуществлять дифференциальное регулирование.
Если выход увеличивается, то входной сильфон и нижний дифференциальный сильфон расширяются. Верхний дифференциальный сильфон расширяется позднее из-за переменного ограничения. Балансир поворачивается, и выход немедленно повышается.
Когда входной сигнал полностью перетечет в верхний дифференциальный сильфон, этот сильфон приложит силу, которая уничтожит силу, приложенную нижним дифференциальным сильфоном.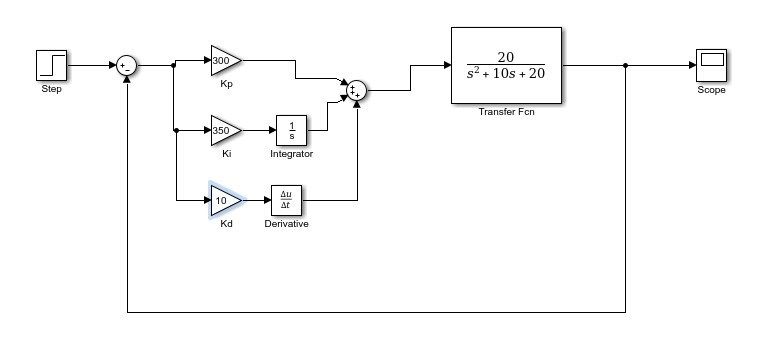
На этой точке дифференциальное регулирование прекращается. В то же время, когда это происходит, сильфон обратной связи расширяется в результате изменения выхода. Изменение выхода подается на интегральный сильфон, который вызывает силу, стремящуюся удержать клапан ближе к соплу. Это действие держит выход на высоком уровне в течение времени, когда переменная процесса не равна уставке. Выход будет продолжать увеличиваться до тех пор, пока переменная процесса не вернется в заданному значению уставки.
ПИД-регулятор будет хорошим выбором для работающей на газе печи для подогрева нефти, потому что последующий процесс, куда поступает подогретая нефть, допускает лишь очень маленькие отклонения температуры нефти от заданного значения, а большие запаздывания в процессе подогрева делают очень трудной задачу определения и устранения отклонений.
Газовая печь для подогрева нефтиОдна из причин запаздывания — емкость. Печь имеет способность сохранять большое количество тепла внутри своих стенок.
Накопленная теплота передается к нефти, но передача не происходит мгновенно. Если внутренние стенки нагреты слишком сильно, потребуется некоторое время для понижения их температуры, в течение которого нефть может быть перегрета. Если внутренние стенки не достаточно нагреты, то нефть может не получить достаточно тепла.
Дифференциальная составляющая ПИД-регулятора помогает преодолевать запаздывания посредством выработки эффективных упреждающих воздействий. Интегральная составляющая непрерывно корректирует выходной сигнал при наличии смещения пока регулируемая температура не возвращается к уставке.
Двухпозиционное регулирование регулирование, при котором регулирующий орган перемещается из одного крайнего положения в другое и обратно: включено или выключено
Дифференциальное регулирование выработка составляющей выходного сигнала регулятора в зависимости от скорости отклонения регулируемой переменной
Интегральное регулирование формирует регулирующее воздействие пропорционально интегралу отклонения регулируемой величины так долго, пока существует отклонение
Пропорциональное регулирование способ регулирования, при котором характеристики выходного сигнала пропорциональны характеристикам входного сигнала
Исполнительный механизм устройство, преобразующее выходной сигнал регулятора в перемещение регулирующего органа
» Перейти к дополнительным материалам
В этой серии статей мы рассмотрим, как реализовать как аналоговые, так и цифровые системы управления.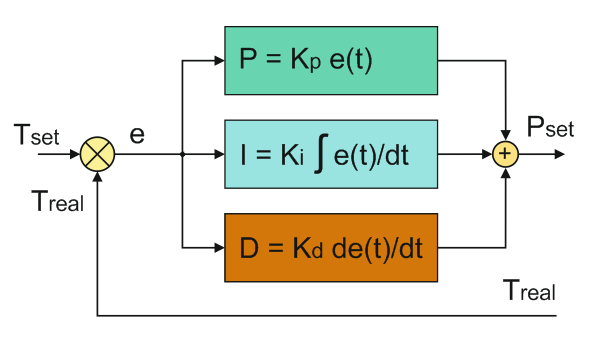
Мы будем использовать ПИД-регулятор (пропорционально-интегрально-дифференциальный). С помощью ПИД-регулятора мы можем управлять тепловыми, электрическими, химическими и механическими процессами. ПИД-регулятор находится в основе многих промышленных систем управления.
В этой первой из трех статей мы ответим на вопросы «почему». Мы также заложим основу, чтобы лучше понять, что такое ПИД-регулятор. В последующих частях мы рассмотрим, как настроить ПИД-регулятор и как реализовать цифровой ПИД-регулятор с помощью ZILOG Encore! микропроцессор.
Цель этой серии — познакомить вас с миром управляющей электроники. Концепции будут объяснены простым, интуитивно понятным способом, и будут представлены полезные практические примеры. Математика будет сведена к абсолютному минимуму. Это не значит, что математика не важна. Наоборот, системы управления можно моделировать и анализировать математически. Математика не что иное, как удивительно, и я бы посоветовал вам внимательно изучить ее.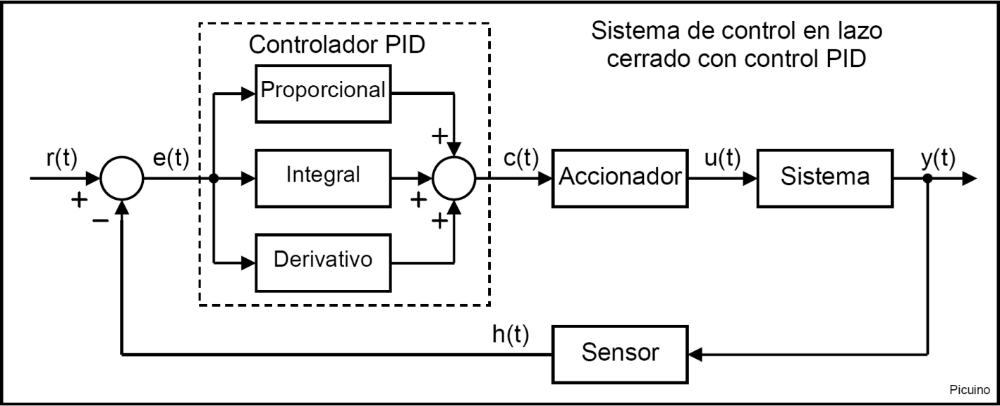
Существуют сотни книг, объясняющих теорию и математику систем управления. Эти книги познакомят вас с мощными инструментами, такими как преобразования Лапласа, корневое геометрическое место и графики Боде. Опять же, эта серия статей едва касается поверхности. Еще многое предстоит узнать.
Термин PID является аббревиатурой от Proportional Integral Derivative. ПИД-регулятор является частью системы обратной связи. Система PID использует пропорциональные, интегральные и производные элементы привода для управления процессом. Некоторые из вас уже знают, что означают P, I и D. Не волнуйтесь, если вы этого не сделаете; мы скоро рассмотрим эти термины с простыми для понимания примерами.
Вам нужен PID, потому что есть некоторые вещи, которые трудно контролировать стандартными методами. Позвольте мне проиллюстрировать это примером. Мой первый опыт работы с системами управления оказался неудачным. Моя цель состояла в том, чтобы регулировать мощность источника питания с помощью микроконтроллера PIC.
PIC считывал выходное напряжение с помощью АЦП и настраивал ШИМ для регулирования выходного сигнала. Стратегия управления была очень проста: если напряжение было ниже заданного значения, включить ШИМ. Если измеренное напряжение было выше уставки, то отключите ШИМ. Блок питания PIC почти заработал. Он действительно производил выходное напряжение постоянного тока, которое я хотел. К сожалению, он также имеет значительные пульсации переменного тока на сигнале постоянного тока.
Стратегия управления, которую я только что описал, называется включением-выключением или релейным управлением. Многие типы систем используют эту стратегию управления. Возьмем, к примеру, печь в моем доме. Когда температура ниже заданной, печь включается. Когда температура выше заданной, печь выключается. Как и в моем блоке питания, график зависимости температуры от времени представляет собой синусоиду.
Для некоторых видов контроля допустимо; для других это не так. Вы не хотели бы использовать этот тип управления для серводвигателя — случались бы плохие вещи! Только представьте — двигатель будет работать на полную мощность в одном направлении, а в следующий момент — на полной мощности в другом направлении.
Вы можете видеть, откуда взялся термин bang-bang. Этот сервопривод долго не протянет!
ПИД-регулятор выводит системы управления на новый уровень. Он может обеспечить управляемый — почти интеллектуальный — привод для систем. Теперь мы рассмотрим отдельные компоненты PID-системы. Этот шаг необходим для понимания всей системы PID. Пожалуйста, не пропускайте этот раздел; вы должны знать, как функционируют отдельные компоненты, чтобы понять систему в целом.
Это просто. Пропорциональная составляющая — это просто усиление. Мы можем использовать инвертирующий операционный усилитель, как показано на рис. 9.0030 Рисунок 1 .
РИСУНОК 1.
В этой схеме операционного усилителя коэффициент усиления определяется значениями резисторов. У нас есть следующее математическое соотношение:
V out = -V in * R f /R i
Интеграл — сокращение от интегрирования.
Вы можете думать об этом как о накоплении (добавлении) количества с течением времени. Например, сейчас вы интегрируете эту информацию в свою базу знаний. В вашем хранилище знаний есть компоненты как времени, так и знаний. Очевидно, что все мы начинали как младенцы, практически ничего не зная. Со временем мы интегрировали знания в наш мозг.
В нашем ПИД-регуляторе мы интегрируем напряжение с течением времени. Схема цепи интегратора показана на рис. 2 .
РИСУНОК 2.
Выходное напряжение математически описывается следующим уравнением: напряжения и времени. Рассмотрим работу идеального интегратора. Мы можем упростить математику, сделав член 1/RC равным 1 (т. е. пусть R = 100 кОм и C = 10 мкФ). Рисунок 3 иллюстрирует отношения ввода/вывода интегратора.
РИСУНОК 3.
В интервале времени от 0 до 2 секунд подайте прямоугольную волну 2 В на вход интегратора.
Выход интегратора в конце этого периода времени составляет -4 В (помните, что схема инвертирует). Интегратор накопил сигнал 2 В за 2 секунды. Площадь равна 4. От Т2 до Т4 на интегратор не подается напряжение. Выход без изменений. В оставшейся части этой диаграммы вы можете видеть, что выход интегратора меняет полярность, когда полярность входного сигнала меняется.
В предыдущем обсуждении предполагался идеальный интегратор. Настоящие конденсаторы будут иметь некоторую утечку и будут иметь тенденцию к саморазряду. Кроме того, настоящие операционные усилители могут заряжать конденсатор без входа. Если схема построена так, как нарисовано, она, скорее всего, насытится через несколько минут работы. Чтобы предотвратить это насыщение, добавьте резистор параллельно конденсатору. Для наших целей нас не интересует насыщенность. Мы будем использовать интегратор с другими схемами для управления зарядом конденсатора.
Чтобы лучше понять интегратор, давайте рассмотрим типичное приложение.
Интеграторы часто встречаются в усилителях звука высокого класса.
РИСУНОК 4.
В этом приложении они называются сервоприводами постоянного тока. Типичное применение показано на рис. 5 .
РИСУНОК 5.
Целью этой схемы является удаление нежелательного постоянного напряжения с выхода аудиоусилителя. Любое постоянное напряжение на выходе усилителя будет стремиться зарядить конденсатор интегратора. Затем интегратор изменяет смещение аудиоусилителя, чтобы удалить постоянную составляющую. Резистор и конденсатор подобраны так, чтобы схема не реагировала на звуковые частоты.
Также помните, что форма сигнала переменного тока симметрична. Часть выше 0 имеет тенденцию заряжать конденсатор, в то время как часть ниже разряжает конденсатор. Поэтому, когда вы интегрируете сигнал переменного тока в течение большого промежутка времени, вы получаете 0. Даже небольшое постоянное напряжение будет заряжать конденсатор в течение длительного периода времени, тем самым изменяя смещение усилителя.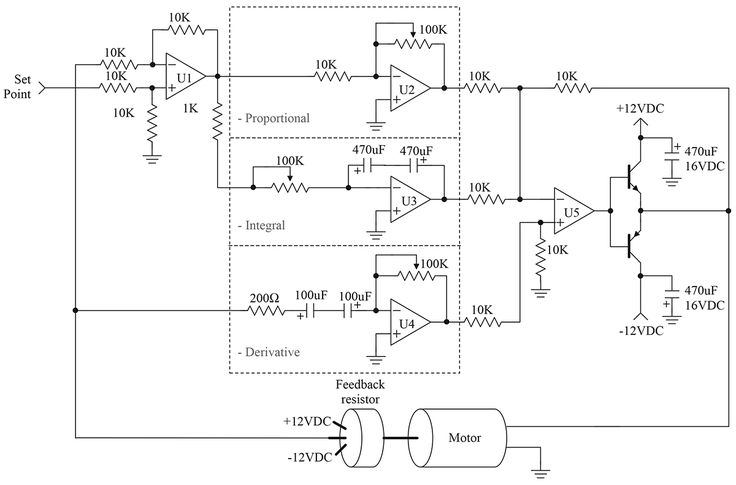
Производная – это показатель скорости изменения. Идеальный дифференциатор показан на Рис. 5 . Эта схема похожа на фильтры верхних частот, которые вы видели на других схемах. Низкие частоты ослабляются, а высокие пропускаются. Математика, которая описывает дифференциатор:
V out = -RC * (скорость изменения)
Скорость изменения эквивалентна измерению наклона линии. Наклон — это мера изменения напряжения, деленная на изменение во времени. В математических терминах это называется дельта-напряжение по отношению к дельта-времени или просто dv/dt. Если мы применим линейное изменение к дифференциатору, мы получим постоянное выходное напряжение постоянного тока. Рисунок 6 иллюстрирует отношение ввода/вывода дифференциатора.
РИСУНОК 6.
Для упрощения математики примем RC=1. От времени 0 до 2 напряжение изменяется на -4 вольта, а время изменяется на 2 секунды.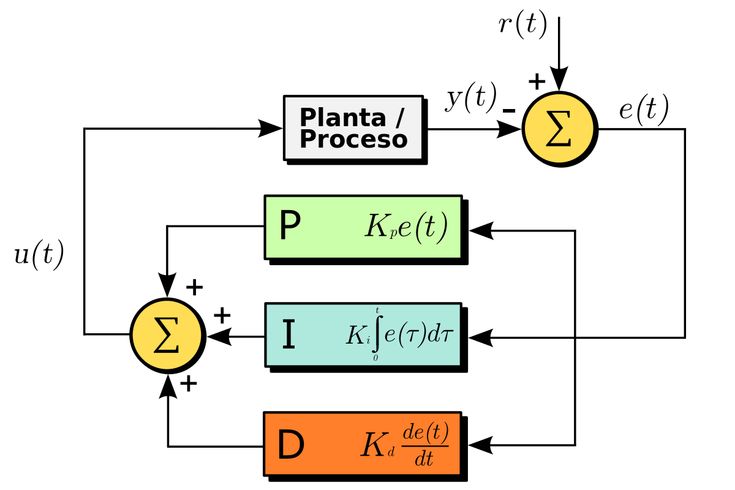
Следовательно, наклон этой линии равен -2. Выход дифференциатора будет равен 2 — помните, что каскад инвертирующий.
Теперь, когда мы познакомились с терминами P, I и D, давайте рассмотрим, как они объединяются в законченную систему. Мы будем использовать ПИД-регулятор для управления серводвигателем постоянного тока. Я использовал серводвигатель марки Hitec, который обычно используется в радиоуправляемых моделях автомобилей и самолетов. Этот сервопривод недорог и легко доступен. Вы также можете приобрести сменные шестерни — подробнее об этом в следующем выпуске!
Сервомеханизм состоит из нескольких компонентов, как показано на Фото 1 .
ФОТО 1.
У нас есть двигатель постоянного тока, набор шестерен и переменный резистор. Резистор прикреплен к последней шестерне. Этот переменный резистор используется для определения положения вращения двигателя.
Сервопривод выпотрошен.
Я использовал только двигатель и переменный резистор, как показано на Фото 2 .
ФОТО 2.
Блок-схема, показывающая функциональные связи ПИД-регулятора, показана на рис. 7 .
РИСУНОК 7.
Первое, на что следует обратить внимание, это параллельный процесс. Условия P, I и D рассчитываются независимо, а затем добавляются к лету Σ. Входом в этот контур является заданное значение — в этом приложении оно может находиться в диапазоне от –12 до +12 В постоянного тока. Результатом является положение двигателя. Положение измеряется резистором и обратной связью как напряжение от –12 до 12 В постоянного тока. Теперь мы рассмотрим каждый из терминов PID независимо, чтобы увидеть, как они связаны. Для этого обсуждения предположим, что уставка равна 0 В постоянного тока.
В крайнем левом углу Рисунок 7 мы видим суммирующий узел.
Разница между уставкой и обратной связью является ошибкой системы. Если измеренное положение двигателя положительное относительно того, где оно должно быть, ошибка будет отрицательной (т. е. требуется отрицательная коррекция). Аналогичным образом, если измеренное положение двигателя равно -1, ошибка будет положительной 1 (т. е. требуется положительная коррекция — помните, что заданное значение равно 0 В постоянного тока).
Ошибка умножается на усиление пропорционального блока. Обратите внимание, что на блок-диаграмме это показано как отрицательное усиление. Это было сделано для того, чтобы блок-схема и схема (представленная позже) согласовывались друг с другом. Выход пропорционального усилителя направляется на второй суммирующий узел, где снова меняется знак. Усилитель загружает ток сигнала и приводит в движение двигатель.
Эта цепочка получается довольно длинной, поэтому давайте резюмируем пропорциональную операцию в нескольких простых предложениях:
Переходим к интегралу. Интеграл — это устройство, которое заряжает конденсатор в течение определенного периода времени. Вспомните пример аудиоусилителя. В этом приложении интегратор накапливал выходной постоянный ток усилителя с течением времени. Затем он перенастроил усилитель, чтобы устранить ошибку по постоянному току. В цепи в Рисунок 7 , интегратор выполняет ту же задачу. Это интеграция ошибки. Затем он подает корректирующий сигнал на двигатель. Мы можем резюмировать интегральное действие в нескольких предложениях:
Конечная составляющая PID является производной. Напомним, что выходной сигнал дифференциатора был пропорционален наклону волны. В этой цепи происходит тот же тип действия. Когда двигатель начинает вращаться, напряжение, измеряемое резистором, будет увеличиваться или уменьшаться. Если у нас есть изменение напряжения в течение определенного периода времени, у нас есть рампа! Наклон этой рампы изменяется в зависимости от скорости двигателя. Если двигатель вращается быстро, крутизна будет высокой (т. е. напряжение быстро меняется в течение заданного промежутка времени). Следовательно, выход производной ступени будет высоким. Дифференциатор имеет следующие атрибуты:
Соединения для дифференциатора отличаются от соединений пропорциональной и интегральной частей. Дифференциатор получает вход непосредственно от резистора. Поэтому он измеряет только скорость, с которой движется двигатель. Он не заботится о заданной точке. Это делается для предотвращения больших дифференциальных управляющих сигналов при изменении уставки. Опять же, дифференциатор реагирует только на скорость двигателя.
Рисунок 8 содержит упрощенную схему системы ПИД-регулирования серводвигателя.
РИСУНОК 8.
Эта схема является адаптацией ПИД-регулятора, представленного профессором Джейкобом в его книге Электроника промышленного управления . Этот тип системы имеет преимущество в простоте настройки. Эта схема также проста и легка в построении.
Схема имеет ту же физическую структуру, что и блок-схема. Операционный усилитель U1 используется в качестве суммирующего узла для заданного значения и измеренного положения двигателя.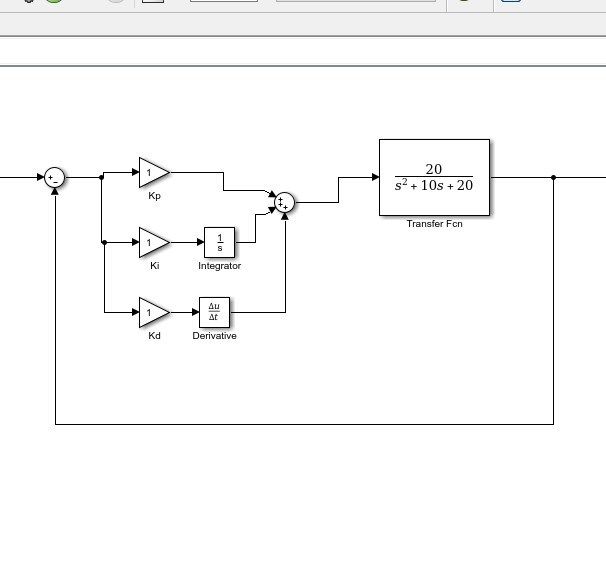
Отдельные функции P, I и D реализуются U2, U3 и U4 соответственно. Наконец, операционный усилитель U5 суммирует отдельные члены ПИД-регулятора. Члены P и I меняются местами, а член D — нет. Транзисторы Дарлингтона были добавлены к U5 для увеличения тока до уровня, достаточного для привода двигателя.
Отдельные компоненты P, I и D выглядят так, как они были представлены ранее в этой статье. Каждый из членов имеет переменный резистор для регулировки коэффициента усиления. Регулировка (настройка) этой схемы является темой для следующего выпуска.
Выбор компонентов для этой схемы не важен. Переменные резисторы должны быть многооборотными для удобства регулировки. Можно использовать операционные усилители общего назначения; однако U3 должен быть входным типом FET. Конструкция полевого транзистора лучше подходит для интегратора, поскольку она не будет самозаряжать конденсатор интегратора. Я обнаружил, что счетверенный операционный усилитель, такой как LF347N, идеально подходит для этого приложения.
Для интегратора и производных цепей требуются большие конденсаторы. Большие значения требуют использования электролитических конденсаторов. Электролитический конденсатор можно использовать как неполяризованный, если последовательно подключить два конденсатора, как показано на схеме.
Прежде чем мы сможем протестировать схему ПИД-регулятора, нам нужно больше узнать о механической системе. Нам нужно знать, как он реагирует на команду и как взаимодействуют отдельные термины P, I и D. Придется набраться терпения и дождаться следующей партии. А пока займитесь макетом схемы. Вы можете использовать генератор функций для проверки отдельных этапов. Посмотрите, как отдельные каскады реагируют на синусоидальные, прямоугольные и треугольные сигналы. Не забудьте использовать низкую частоту — менее 10 Гц. Эта частота примерно такая же, как и в системе серводвигателя.
Оставайтесь с нами; в следующий раз мы научимся настраивать ПИД-регулятор. Мы добавим дополнительную схему, чтобы предотвратить состояние, называемое интегральной обмоткой.
Кроме того, ждите третьей части, в которой мы реализуем PID на ZILOG Encore! микроконтроллер. NV
ПИД-регулятор 2005-01 (рис. 8)
В типичной системе управления переменная процесса представляет собой системный параметр, которым необходимо управлять, например, температура (ºC), давление (psi) или скорость потока (литры/мин) . Датчик используется для измерения переменной процесса и обеспечения обратной связи с системой управления. Заданное значение — это желаемое или заданное значение переменной процесса, например 100 градусов Цельсия в случае системы контроля температуры.
В любой момент времени разница между переменной процесса и заданным значением используется алгоритмом системы управления 9.0265 (компенсатор) , чтобы определить желаемую выходную мощность привода для управления системой (установкой). Например, если измеренная переменная процесса температуры составляет 100 ºC, а желаемая уставка температуры составляет 120 ºC, то выход привода , заданный алгоритмом управления, может управлять нагревателем. Приведение в действие исполнительного механизма для включения нагревателя приводит к тому, что система нагревается, что приводит к увеличению технологической переменной температуры. Это называется системой управления с замкнутым контуром, потому что процесс считывания показаний датчиков для обеспечения постоянной обратной связи и расчета требуемой выходной мощности исполнительного механизма повторяется непрерывно и с фиксированной скоростью цикла, как показано на рисунке 1.9.0003
Во многих случаях выход привода — не единственный сигнал, влияющий на систему.
Например, в температурной камере может быть источник холодного воздуха, который иногда дует в камеру и нарушает температуру. Такой термин называется возмущением . Обычно мы пытаемся спроектировать систему управления так, чтобы свести к минимуму влияние возмущений на переменную процесса.
Рис. 1: Блок-схема типичной замкнутой системы.
Процесс разработки системы управления начинается с определения требований к производительности. Производительность системы управления часто измеряется путем применения ступенчатой функции в качестве командной переменной уставки, а затем измерения отклика переменной процесса. Обычно ответ определяется количественно путем измерения определенных характеристик сигнала. Время нарастания — это количество времени, которое требуется системе для перехода от 10% к 90% установившегося или конечного значения. Процент превышения — это величина превышения переменной процесса конечного значения, выраженная в процентах от конечного значения.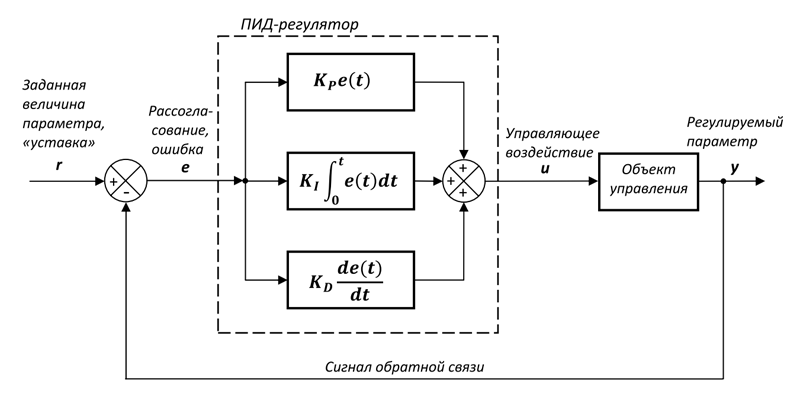
Время установления — это время, необходимое для того, чтобы переменная процесса установилась в пределах определенного процента (обычно 5 %) от конечного значения. Установившаяся ошибка — это окончательная разница между переменной процесса и заданным значением. Обратите внимание, что точное определение этих величин будет различаться в промышленности и научных кругах.
Рис. 2: Реакция типичной замкнутой системы ПИД-регулятора.
После использования одной или всех этих величин для определения требований к характеристикам системы управления полезно определить наихудшие условия, при которых ожидается, что система управления будет соответствовать этим проектным требованиям. Часто в системе возникает возмущение, которое влияет на переменную процесса или измерение переменной процесса. Важно разработать систему управления, которая удовлетворительно работает в наихудших условиях. Мера того, насколько хорошо система управления способна преодолевать последствия возмущений, называется 9.
0265 Отказ от помех системы управления.
В некоторых случаях реакция системы на заданный управляющий выход может меняться со временем или в зависимости от какой-либо переменной. Нелинейная система представляет собой систему, в которой параметры управления, дающие желаемую реакцию в одной рабочей точке, могут не дать удовлетворительной реакции в другой рабочей точке. Например, камера, частично заполненная жидкостью, будет демонстрировать гораздо более быструю реакцию на мощность нагревателя, когда она почти пуста, чем когда она почти заполнена жидкостью. Мера того, насколько хорошо система управления будет выдерживать помехи и нелинейности, называется надежность системы управления.
Некоторые системы демонстрируют нежелательное поведение, называемое deadtime . Мертвое время — это задержка между изменением переменной процесса и моментом, когда это изменение можно наблюдать. Например, если датчик температуры расположен далеко от впускного клапана для холодной воды, он не будет измерять изменение температуры немедленно, если клапан открыт или закрыт.