Пид регулятор схема: ПИД-регуляторы – для чайников-практиков / Теория, измерения и расчеты / Сообщество EasyElectronics.ru

ПИД-регулятор своими руками / Хабр

; PID управление
CalcMainEnd:
	; Вычисления, Go-Go.
CalcPid:
	;	1. Eo = E				 | 16bit
Pid1:
	MOV Err0H, ErrH
	MOV Err0L, ErrL
	;	2. E = Y-X				 | 16bit
Pid2:
	CLR C
	MOV A, SettingL
	SUBB A, ThermoL
	MOV ErrL, A
	MOV A, SettingH
	SUBB A, ThermoH
	MOV ErrH, A
	JNB  OV, Pid2Ov
	JB	ACC.7, Pid2Max
Pid2Min:
	MOV ErrL, #LOW(-500*32)
	MOV ErrH, #HIGH(-500*32)
	SJMP Pid2End
Pid2Max:
	MOV ErrL, #LOW(500*32)
	MOV ErrH, #HIGH(500*32)
	SJMP Pid2End
Pid2Ov:
	JNB ACC.7, Pid2OvP
Pid2OvN: ; Проверим на ограничение вниз
	CLR C
	MOV A, ErrL
	SUBB A, #LOW(-500*32)
	MOV A, ErrH
	SUBB A, #HIGH(-500*32)
	JNC Pid2End ; Если > -500 => всё ок
	SJMP Pid2Min
Pid2OvP:
	CLR C
	MOV A, ErrL
	SUBB A, #LOW(500*32)
	MOV A, ErrH
	SUBB A, #HIGH(500*32)
	JNC Pid2Max ; Если < 500 => всё ок
Pid2End:

	;	3. Int = Int + (E+Eo)/2  | 32bit+16bit
Pid3:
	JNB PowerReady, Pid3End ; Если нет сети -- интегральную часть не копим
	MOV A, ErrL
	ADD A, Err0L
	MOV R0, A ; временно
	MOV A, ErrH
	ADDC A, Err0H
	MOV C, ACC.7 ; Полусумма всегда влезает в 16 бит, поэтому при сдвиге надо сохранить знак
	RRC A	; Поделим без потери знака
	XCH A, R0 ; A= младшая часть, R0 - старшая часть полусуммы
	RRC A	; Доделили
	JNB  IntS, Pid3IntPos
	; Int отрицательный, изменим знак для R0:A, тем самым можно будет просто сложить с Int
	CLR C
	CPL A
	ADD A, #1
	XCH A, R0
	CPL A
	ADDC A, #0
	XCH A, R0
Pid3IntPos:
	; У Int и R0:A сейчас согласованы знаки, поэтому складываем обычным образом
	ADD A, IntLL
	MOV IntLL, A
	MOV A, IntLH
	ADDC A, R0
	MOV IntLH, A
	MOV A, R0
	JB	ACC.7, Pid3Neg ; Прибавляли отрицательную разность?
	; Если разность положительная, просто распространим перенос
	JNC jPid3End  ; Если прибавили слово и переноса небыло -- делать нам ничего не требуется.
	INC IntHL ; Распространяем перенос выше
	MOV A, IntHL
	JNZ Pid3End  ; Если перенос не ушел в 4й байт -- всё нормально
	INC IntHH ; Распространяем перенос на САМЫЙ старший байт
	MOV A, IntHH
	JNZ Pid3End  ; Если перенос не ушел еще выше -- всё нормально
	MOV IntHH, #0FFh ; Если перенс был выше -- ограничиваем интеграл потолком
	MOV IntHL, #0FFh
	MOV IntLH, #0FFh
	MOV IntLL, #0FFh
jPid3End:
	SJMP Pid3End
Pid3Neg: ; Если разность отрицательная, то надо продолжать добавлять оба раза, но FFh
	MOV A, IntHL
	ADDC A, #0FFh
	MOV IntHL, A
	MOV A, IntHH
	ADDC A, #0FFh
	MOV IntHH, A
	JC	Pid3End  ; Если тут был перенос, значит знак интеграла не изменился
	CPL IntS ; Если переноса небыло, значит у интеграла изменился знак
	CPL C		 ; Обратим знак получившегося числа
	MOV A, #0
	SUBB A, IntLL
	MOV IntLL, A
	MOV A, #0
	SUBB A, IntLH
	MOV IntLH, A
	MOV A, #0
	SUBB A, IntHL
	MOV IntHL, A
	MOV A, #0
	SUBB A, IntHH
	MOV IntHH, A
	; так как оно стало отрицательным -- то перенос тут будет всегда
Pid3End:

	;	5. cI = Int*(1/Ti)		 | 32*32=>32bit
Pid5: ; R3:R2:R1:R0 = Int*(1/Ti)
	JB Ti_sh2, Pid5Calc ; если Ti_sh2=0, то 1/Ti=1 или Ti=0. и ничего делать не надо
	MOV A, Ti_mLL
	ORL A, Ti_mLH
	ORL A, Ti_mHL
	ORL A, Ti_mHH
	JZ	Pid5Zero
	MOV R0, IntLL
	MOV R1, IntLH
	MOV R2, IntHL
	MOV R3, IntHH
	AJMP Pid5End
Pid5Zero:
	MOV A, #0
	MOV R0, A
	MOV R1, A
	MOV R2, A
	MOV R3, A
	MOV IntLL, A
	MOV IntLH, A
	MOV IntHL, A
	MOV IntHH, A
	AJMP Pid5End
Pid5Calc:
	; R7:R6:R5:R4[:R3] = MULUH(Int*Ti_m) // R3 считаем как часть для округления
	MOV R2, #0
	;; R7:R6 = IntHH*Ti_mHH
	MOV A, IntHH
	MOV B, Ti_mHH
	MUL AB
	MOV R7, B
	MOV R6, A
	; R6:R5 += IntHL*Ti_mHH
	MOV A, IntHL
	MOV B, Ti_mHH
	MUL AB
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R5:R4 += IntLH*Ti_mHH
	MOV A, IntLH
	MOV B, Ti_mHH
	MUL AB
	MOV R4, A
	MOV A, R5
	ADD A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntLL*Ti_mHH
	MOV A, IntLL
	MOV B, Ti_mHH
	MUL AB
	MOV R3, A
	MOV A, R4
	ADD A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R6:R5 += IntHH*Ti_mHL
	MOV A, IntHH
	MOV B, Ti_mHL
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADDC A, B
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R5:R4 += IntHL*Ti_mHL
	MOV A, IntHL
	MOV B, Ti_mHL
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntLH*Ti_mHL
	MOV A, IntLH
	MOV B, Ti_mHL
	MUL AB
	MOV A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R5:R4 += IntHH*Ti_mLH
	MOV A, IntHH
	MOV B, Ti_mLH
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntHL*Ti_mLH
	MOV A, IntHL
	MOV B, Ti_mLH
	MUL AB
	ADD A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R4:R3 += IntHH*Ti_mLL
	MOV A, IntHH
	MOV B, Ti_mLL
	MUL AB
	ADD A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;;; Если R3 > 7F --
	MOV A, R3
	JNB ACC.7, Pid5Shift ; Если R3<80 -- округление не надо
	ANL A, #7Fh
	JZ	Pid5Round ; Если = 80 -- округляем до нечетного
	MOV A, #1
	ADD A, R4
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	SJMP Pid5Shift
Pid5Round:
	MOV A, R4
	ORL A, #01h
	MOV R4, A
	;JMP Pid5Shift

Pid5Shift:
	; R3:R2:R1:R0 = (Int-R7:R6:R5:R4) >> 1
	CLR C
	MOV A, IntLL
	SUBB A, R4
	MOV R0, A
	MOV A, IntLH
	SUBB A, R5
	MOV R1, A
	MOV A, IntHL
	SUBB A, R6
	MOV R2, A
	MOV A, IntHH
	SUBB A, R7
	RRC A ; >>1 без потери переноса
	MOV R3, A
	MOV A, R2
	RRC A
	MOV R2, A
	MOV A, R1
	RRC A
	MOV R1, A
	MOV A, R0
	RRC A
	;MOV R0, A
	; R3:R2:R1:R0 += R7:R6:R5:R4
	;MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R1
	ADDC A, R5
	MOV R1, A
	MOV A, R2
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	ADDC A, R7
	MOV R7, A
	; Теперь сдвинуть вправо на sh3.
	; sh3 может быть до 16 (так как у нас Ti 16разрядный; проверим необходимость сдвига на 16 бит)
	MOV A, Ti_sh3
	JNB ACC.4, Pid5ShiftUnder16
	; Надо сдвинуть >=16 -- 2 байта сдвинем mov'ами
	MOV R0, 18h+2; R2, bank 3
	MOV R1, 18h+3; R3, bank 3
	MOV R2, #0
	MOV R3, #0
Pid5ShiftUnder16:
	JNB ACC.3, Pid5ShiftUnder8
	; Надо сдвинуть на >=8 -- 1 байт сдвигаем mov'ами
	MOV R0, 18h+1; R1, bank 3
	MOV R1, 18h+2; R2, bank 3
	MOV R2, 18h+3; R3, bank 3
	MOV R3, #0
Pid5ShiftUnder8:
	ANL A, #07h
	JZ Pid5End ; Если внутри байта двигать не надо -- всё
	MOV R4, A
	SJMP Pid5ShiftRight
Pid5NextShift:
	CLR C
	; К этому моменту C у нас еще возможнозначимый старший бит!
Pid5ShiftRight:
	MOV A, R3
	RRC A
	MOV R3, A
	MOV A, R2
	RRC A
	MOV R2, A
	MOV A, R1
	RRC A
	MOV R1, A
	MOV A, R0
	RRC A
	MOV R0, A
	DJNZ R4, Pid5NextShift
	; Всё, после всех сдвигов получили результат
	; Не забываем, что у вычисленного в R3:R2:R1:R0
	; сейчас число положительное, а знак его в IntS
Pid5End:

	;	4. PID += [ cD = Td * (E-Eo) ]		| 16*16=>32bit
Pid4: ; cD = R7:R6:R5:R4; ErrD = E-Eo
	CLR C
	MOV A, ErrL
	SUBB A, Err0L
	MOV DiffL, A
	MOV A, ErrH
	SUBB A, Err0H
	MOV DiffH, A
	MOV C, ACC.7 ; Берём знак результата
	MOV DiffS, C ; Сохраним знак E-Eo
	JNC Pid4Mul
	; Diff -- орицательный, обратим знак
	MOV A, DiffL
	CPL A
	ADD A, #1
	MOV DiffL, A
	MOV A, DiffH
	CPL A
	ADDC A, #0
	MOV DiffH, A
Pid4Mul:
	; R7:R6 = DiffH*TdH
	; MOV A, DiffH = в любом случае A=DiffH
	MOV B, TdH
	MUL AB
	MOV R6, A
	MOV R7, B
	; R5:R4 = DiffL*TdL
	MOV A, DiffL
	MOV B, TdL
	MUL AB
	MOV R4, A
	MOV R5, B
	; R6:R5 += DiffH*TdL
	MOV A, DiffH
	MOV B, TdL
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R7
	ADDC A, #0
	MOV R7, A
	; R6:R5 += DiffL*TdH
	MOV A, DiffL
	MOV B, TdH
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R7
	ADDC A, #0
	MOV R7, A

	;	6. PID = E + cI + cD	 | 32bit
Pid6:	; R3:R2:R1:R0 равно cI, знак в IntS;
	; R7:R6:R5:R4 = cD; знак в DiffS
	; E в обратном дополнительном коде

	JB IntS, ChkDiffN
	JNB DiffS, Pid6Add ; Int>0, Diff>0 => Add
	SJMP Pid6Sub ; Int>0, Diff<0 => Sub
ChkDiffN:
	JNB DiffS, Pid6Sub ; Int<0, Diff>0 => Sub
	; Int<0, Diff<0 => Add
Pid6Add:
	; Одинаковый знак => складываем их с проверкой на переполнение
	MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R1
	ADDC A, R5
	MOV R1, A
	MOV A, R2
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	ADDC A, R7
	MOV R3, A
	JNC Pid6Err ; Если нет переноса - в результате сложения переполнения небыло
	MOV R3, #0FFh
	MOV R2, #0FFh
	MOV R1, #0FFh
	MOV R0, #0FFh
	SJMP Pid6Err
Pid6Sub:
	; Знаки разные -- вычтем одно из другого и проверим знак результата
	CLR C
	MOV A, R4
	SUBB A, R0
	MOV R0, A
	MOV A, R5
	SUBB A, R1
	MOV R1, A
	MOV A, R6
	SUBB A, R2
	MOV R2, A
	MOV A, R7
	SUBB A, R3
	MOV R3, A
	JNC Pid6Err ; Если нет заимствования -- знак результата равен знаку DiffS
	CPL DiffS ; Если заимствование было, у DiffS и результата надо обратить знак
	MOV R6, #0 ; R6=0
	MOV A, R0
	CPL A
	ADDC A, R6 ; R6=0, C=1 => действие +1
	MOV R0, A
	MOV A, R1
	CPL A
	ADDC A, R6 ; +перенос
	MOV R1, A
	MOV A, R2
	CPL A
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	CPL A
	ADDC A, R6
	MOV R3, A

Pid6Err:
	MOV R6, #0 ; R6=0
	; В R3:R2:R1:R0 -- лежит cI+cD; знак суммы в DiffS
	; надо прибавить/отнять Err, записанное в обратном коде
	; Приведём знак Err к DiffS
	MOV R4, ErrL
	MOV A, ErrH
	JB ACC.7, Pid6ChkDiffS
	JNB DiffS, Pid6SumErrNoInv ; Err>0, Diff>0 => NoInv
	SJMP Pid6SumErrInv
Pid6ChkDiffS:
	JNB DiffS, Pid6SumErrNoInv ; Err<0, Diff>0 => NoInv
Pid6SumErrInv:
	; У Err знак отличается от DiffS -- инвертируем
	SETB C ; Не уверен в состоянии C
	MOV A, ErrL
	CPL A
	ADDC A, R6 ; A+=R6+C, R6=0	C=1 => A+=1
	MOV R4, A ; R4=ErrL
	MOV A, ErrH
	CPL A
	ADDC A, R6
Pid6SumErrNoInv:
	MOV R5, A ; ErrH
Pid6SumErr:
	; Итак, в R5:R4 лежит Err, знак которого согласован с DiffS; но в обратно-дополнительном коде
	MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R5
	CLR F0
	JNB ACC.7, Pid6SubErrPos
	SETB F0
	MOV R6, #0FFh ; Добавляем отрицательное => дополняем FFами
Pid6SubErrPos:
	ADDC A, R1
	MOV R1, A
	MOV A, R2
	ADDC A, R6 ; +расширение
	MOV R2, A
	MOV A, R3
	ADDC A, R6 ; +расширение
	MOV R3, A
	MOV R6, #0
	; Надо проверить нет ли смены знака итоговой суммы
	JNC Pid6ChkF0
	JB F0, Pid7 ; Err<0, был перенос => Знак не сменился, переполнения нет
	SJMP Pid6SumOv ; Err>0, был перенос => переполнение
Pid6ChkF0:
	JNB F0, Pid7 ; Err>0, небыло переноса => нет переполнения
	;SJMP Pid6SumUf ; Err<0, небыло переноса => сменился знак
Pid6SumUf:
	; Если Err<0 и небыло переноса => сменился знак
	CPL DiffS
	MOV A, R0
	CPL A
	ADD A, #1 ; C=?, поэтому прибавляем 1 обычным методом
	MOV R0, A
	MOV A, R1
	CPL A
	ADDC A, R6
	MOV R1, A
	MOV A, R2
	CPL A
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	CPL A
	ADDC A, R6
	MOV R3, A
	SJMP Pid7 ; Знак у результата и DiffS приведены в норму
Pid6SumOv:
	; Было переполнение => округляем до максимума
	MOV R0, #0FFh
	MOV R1, #0FFh
	MOV R2, #0FFh
	MOV R3, #0FFh

	;	7. U = K*PID/256		 | 32bit*16bit/8bit => 40bit,
	;					 | которые усекаются до 10bit
	;					 | при вычислениях
Pid7: ; В R3:R2:R1:R0 лежит результат PID, в DiffS его знак
	  ; Нужно вычислить K*PID/256, ограничив результат до 10бит
	  ; K всегда положительно, поэтому если PID < 0 => минимум
	JB DiffS, Pid7Umin
	; поскольку мы можем жестко ограничить сверху 16ю битами,
	; то если R3 != 0 => ставим максимум в любом случае
	MOV A, R3
	JNZ Pid7Umax
	; [R2:R1:R0 * KH:HL] = [R7:R6:R5:R4:R3]
	; вычисляем, учитывая что должно получиться R7=0 R6=0,
	; иначе переполнение, поэтому R7 и R6 вообще не трогаем
	; но проверяем результат
	; R7:R6 = R2*KH
	MOV A, R2
	JZ Pid7S1
	MOV A, KH
	JNZ Pid7Umax ; Если R2!=0 и KH!=0 => R7:R6>0 => переполнение
Pid7S1:
	; R6:R5 = R2*KL
	MOV A, R2
	MOV B, KL
	MUL AB
	MOV R5, A
	MOV A, B
	JNZ Pid7Umax ; Если R6 > 0 => переполнение
	; R6:R5 = R1*KH
	MOV A, R1
	MOV B, KH
	MUL AB
	ADD A, R5
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	MOV A, B
	JNZ Pid7Umax ; Если R6 > 0 => переполнение
	; R5:R4 = R0*KH
	MOV A, R0
	MOV B, KH
	MUL AB
	MOV R4, A
	MOV A, R5
	ADD A, B
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R5:R4 = R1*KL
	MOV A, R1
	MOV B, KL
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R4:R3 = R0*KL
	MOV A, R0
	MOV B, KL
	MUL AB
	RLC A ; C = R3>=0x80, Z=R3>0x80
	MOV R3, #0FFh ; R3<>0x80 => ничего
	JNZ Pid7S2
	MOV R3, #0FEh ; R3==0x80 => округление до четного
Pid7S2:
	MOV A, R4
	ADDC A, B ; Складываем умножение, регистр, и перенос-округление
	ANL A, R3 ; А так же если округление до четного -- отбрасываем после младший бит
	MOV R4, A
	MOV A, R5
	ADDC A, R6 ; R6=0 у нас с давних пор, хоть мы туда и не складывали ничего во время перемножения
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R5:R4 => ограниченный в 16 бит результат
	; Теперь надо ограничить R5:R4 до Umax/Umin
	MOV A, UmaxL
	SUBB A, R4 ; C=0 на текущий момент
	MOV A, UmaxH
	SUBB A, R5
	JC Pid7Umax ; Если R5:R4>Umax => R5:R4 = Umax
	MOV A, UminL
	SUBB A, R4 ; C=0 на текущий момент
	MOV A, UminH
	SUBB A, R5
	JNC Pid7Umin ; Если R5:R4<Umin => R5:R4 = Umin
	; Мощность вычислена
	MOV UH, R5
	MOV UL, R4
	SETB UReady
	AJMP CalcExit
Pid7Umax: ; Установить максимальную мощность
	MOV UH, UmaxH
	MOV UL, UmaxL
	SETB UReady
	AJMP CalcExit
Pid7Umin: ; Установить минимальную мощность
	MOV UH, UminH
	MOV UL, UminL
	SETB UReady
	AJMP CalcExit
 
  
  
 
 
 
  
  

что это такое, регулирование температуры ПИД регулятором

Дифференциальный пропорционально-интегральный регулятор — устройство, которое устанавливают в автоматизированных системах для поддержания заданного параметра, способного к изменениям.

На первый взгляд все запутанно, но можно объяснить ПИД регулирование и для чайников, т.е. людей, не совсем знакомых с электронными системами и приборами.

Что такое ПИД регулятор?

ПИД регулятор — прибор, встроенный в управляющий контур, с обязательной обратной связью. Он предназначен для поддержания установленных уровней задаваемых величин, например, температуры воздуха.

Устройство подает управляющий или выходной сигнал на устройство регулирования, на основании полученных данных от датчиков или сенсоров. Контроллеры обладают высокими показателями точности переходных процессов и качеством выполнения поставленной задачи.

Три коэффициента ПИД регулятора и принцип работы

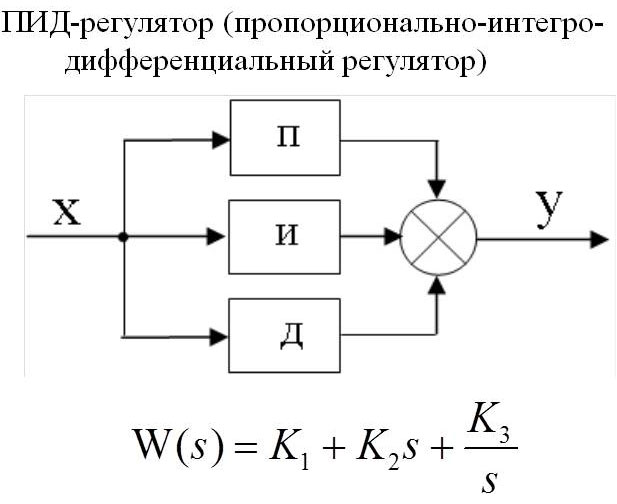
Работа ПИД-регулятора заключается в подаче выходного сигнала о силе мощности, необходимой для поддержания регулируемого параметра на заданном уровне. Для вычисления показателя используют сложную математическую формулу, в составе которой есть 3 коэффициента — пропорциональный, интегральный, дифференциальный.

Возьмем в качестве объекта регулирования ёмкость с водой, в которой необходимо поддерживать температуру на заданном уровне с помощью регулирования степени открытия клапана с паром.

Пропорциональная составляющая появляется в момент рассогласования с вводными данными. Простыми словами это звучит так — берется разница между фактической температурой и желаемой, умножается на настраиваемый коэффициент и получается выходной сигнал, который должен подаваться на клапан. Т.е. как только градусы упали, запускается процесс нагрева, поднялись выше желаемой отметки — происходит выключение или даже охлаждение.

Дальше вступает интегральная составляющая, которая предназначена для того, чтобы компенсировать воздействие окружающей среды или других возмущающих воздействий на поддержание нашей температуры на заданном уровне. Поскольку всегда присутствуют дополнительные факторы, влияющие на управляемые приборы, в момент поступления данных для вычисления пропорциональной составляющей, цифра уже меняется. И чем больше внешнее воздействие, тем сильнее происходят колебания показателя. Происходят скачки подаваемой мощности.

Интегральная составляющая пытается на основе прошлых значений температуры, вернуть её значение, если оно поменялось. Подробнее процесс описан в видео ниже.

А дальше выходной сигнал регулятора, согласно коэффициенту, подается для повышения или понижения температуры. Со временем подбирается та величина, которая компенсирует внешние факторы, и скачки исчезают.

Интеграл используется для исключения ошибок путем расчета статической погрешности. Главное в этом процессе — подобрать правильный коэффициент, иначе ошибка (рассогласование) будет влиять и на интегральную составляющую.

Третий компонент ПИД — дифференцирующий. Он предназначен для компенсации влияния задержек, возникающих между воздействием на систему и обратной реакцией. Пропорциональный регулятор подает мощность до тех пор, пока температура не достигнет нужной отметки, но при прохождении информации к прибору, особенно при больших значениях, ошибки всегда возникают. Это может привести к перегреву. Дифференциал прогнозирует отклонения, вызванные задержками или воздействием внешней среды, и снижает подаваемую мощность заранее.

Настройка ПИД регулятора

Настройка ПИД-регулятора осуществляется 2 методами:

1. Синтез подразумевает вычисление параметров на основании модели системы. Такая настройка получается точной, но требует глубоких познаний теории автоматического управления. Она подвластна только инженерам и ученым. Так как необходимо снимать расходные характеристики и производить кучу расчетов.
2. Ручной способ основывается на методе проб и ошибок. Для этого за основу берутся данные уже готовой системы, вносятся некоторые коррективы в один или несколько коэффициентов регулятора. После включения и наблюдений за конечным результатом проводится изменение параметров в нужном направлении. И так до тех пор, пока не будет достигнут нужный уровень работоспособности.

Теоретический метод анализа и настройки на практике применяются крайне редко, что связано с незнанием характеристик объекта управления и кучей возможных возмущающих воздействий. Более распространены экспериментальные методы на основе наблюдения за системой.

Современные автоматизированные процессы реализуются как специализированные модули под управлением программ для настройки коэффициентов регулятора.

Назначение ПИД регулятора

ПИД регулятор предназначен для поддержания на требуемом уровне некой величины — температуры, давления, уровня в резервуаре, расхода в трубопроводе, концентрации чего-либо и т.д., изменением управляющего воздействия на исполнительные механизмы, такие как автоматические регулирующие клапана, используя для этого пропорциональную, интегрирующую, дифференцирующую величины для своей настройки.

Целью использования является получение точного управляющего сигнала, который способен контролировать большие производства и даже реакторы электростанций.

Пример схемы регулирования температуры

Часто ПИД регуляторы используются при регулировке температуры, давайте на простом примере подогрева воды в ёмкости рассмотрим данный автоматический процесс.

В емкости налита жидкость, которую нужно подогреть до нужной температуры и поддерживать её на заданном уровне. Внутри бака установлен датчик измерения температуры — термопара или термометр сопротивления и напрямую связан с ПИД-регулятором.

Для подогрева жидкости будем подавать пар, как показано ниже на рисунке, с клапаном автоматического регулирования. Сам клапан получает сигнал от регулятора. Оператор вводит значение температурной уставки в ПИД-регуляторе, которую необходимо поддерживать в ёмкости.

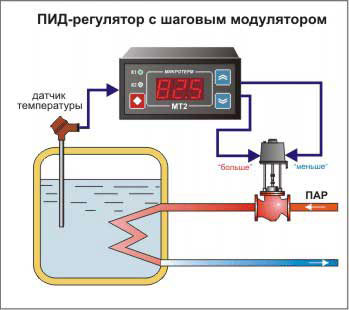
Если настройки коэффициентов регулятора неверны, будут происходить скачки температуры воды, при этом клапан будет то полностью открыт, то полностью закрыт. В этом случае необходимо рассчитать коэффициенты ПИД регулятора и ввести их заново. Если все сделано правильно, через небольшой промежуток времени система выровняет процесс и температура в ёмкости будет поддерживаться на заданной отметке, при этом степень открытия регулирующего клапана будет находиться в среднем положении.

Корректная реализация разностной схемы ПИД регулятора / Хабр

ПИД-регулятор является простейшим регулятором, имеющим эффективные аппаратные аналоговые реализации, и потому применяемый наиболее широко. Для своей работы требует настройки 3х коэффициентов под конкретный объект, позволяющие подобрать процесс регулирования согласно требованиям. Обладая простым физическим смыслом и простой математической записью, применяется широко и часто в регуляторах температуры, регуляторах расхода газа и других системах, где требуется поддерживать некий параметр на заданном уровне, с возможными переходами между разными заданными уровнями. Разумеется, существуют более сложные регуляторы, позволяющие более точно и быстро и с меньшими перерегулированиями выходить на заданные параметры, а так же учитывающие нелинейность или гистерезис регулируемого объекта, однако они обладают большей вычислительной сложностью и сложнее в настройке.

Несмотря на свою простоту как физического смысла, так и математической записи:

при програмной реализаци ПИД регулятора очень часто допускают ошибки, которые встречаются даже в поверенных приборах автоматики.

Причем проверить качество реализации ПИД регулятора крайне легко.

Рассмотрим простейший пример: терморегулятор. Для проверки его качестве лучше всего подходит быстрый, малоинерциальный, маломощный объект. Классика жанра: обычная лампочка на 100Вт с прикрученной к ней тонкой термопарой (ХА). И первое, на чем следует проверять ПИД регулятор — деградация ПИД до просто П-регулятора. То есть коэффициенты интегральной и дифференциальной ставим в ноль, а пропорциональную ставим в максимум.

Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит. Начинаем начинаем увеличивать уставку: 16.1, 16.3, 16.7, 18… 19… лампочка загорелась. Как?! Откуда?! Останавливаемся — выключилась. Итак, мы встретились с первой классической ошибкой реализации ПИД регулятора.

Небольшое математическое отступление: вспомним еще раз интегральную запись указанную выше. Мы реализуем её програмно, а значит — дискретно. То есть с завидной регулярностью производим измерение входной величины, сравниваем её с уставкой, вычисляем воздействие, выдаём, повторить. А значит, надо из интегральной формы перейти в конечно-разностную схему. При переходе обычно используется переход «в лоб»:

где E(n) = X(n) - X0(n) — то есть величина рассогласования между текущим и заданным значением регулируемого параметра.

Использование прямой формулы потребует во-1х считать и хранить интеграл рассогласований за большой период, во-2х требует работы с плавающей точкой высокой точности (так как интегральный коэффициент Ki всегда < 1), либо операции деления (представляя коэффициент в форме 1/Ki) большой разрядности. Всё это требует вычислительных ресурсов, коих в embedded как правило сильно ограничено… Поэтому, вместо реализации прямой схемы, реализуют рекуррентную формулу:

использование рекуррентной формулы позволяет сократить объём вычислений и разрядность промежуточных значений.

Итак, вернёмся к нашему регулятору. Итак, есть регулируемый объект: лампочка. Для управления подаваемой на неё мощностью, используют простой подход: сеть питания (220В 50Гц) подаётся через симистор на нагрузку. Симистор в момент перехода полуволны через ноль выключается, и остаётся выключен до тех пор, пока не будет подан сигнал на управляющий электрод. Таким образом, чем раньше после начала полуволны мы подадим управляющий сигнал, тем больше энергии от этой полуволны достигнет управляемого объекта. Правильно расчитав время для линейности площади части полуволны с момента времени X до конца полуволны, мы получаем возможность выдавать мощность от 0 до 100% с точностью, с которой расчитали таблицу линеаризации.

Итак, мы можем выдавать мощность от 0 до 100%. В реальных объектах, часто нельзя выдавать 100% мощности — например, это черевато перегоранием нагревательного элемента. Поэтому, все приборы имеют настройку минимальной и максимальной выдаваемой мощности на объект.

Итак, после вычисления U(n) по вышестоящей формуле, добавляется еще ограничение результата:
if Un < Umin then Un := Umin; if Un>Umax then Un := Umax;
После чего, вычисленное Un и есть требуемая выходная мощность на текущий момент. Та-дам! Именно вот эта реализация и создаёт ошибку, о которой написано выше.

Причина банальна: в момент перехода от дикретной к конечно-разностной схеме, мы «выносим за скобки» операцию вычисления интеграла, и на каждом шаге мы прибавляем производную к накопленной сумме U(n-1). Наложив же на неё ограничение, мы весь вычисленный интеграл фактически обнуляем. (Ну не сколько обнуляем, сколько приводим к диапазону 0-100, что в данном случае несущественно). Таким образом, мы дифференциурем ПИД регулятор, и остаётся дифференциально-ускорительный. Что в реальности выглядит как просто дифференциальный регулятор — мощность при этом подаётся пропорционально изменению уставки или регулируемой величины, а не пропорционально разности между уставкой и регулируемой величиной.

Вывод №1: вычисление U(n) нельзя ограничивать. Для ограничения мощности подаваемой на выходное устройство следует заводить отдельную переменную.

Теперь, когда мы завели Urn, для ограниченной мощности, перезаливаем, продолжаем тестировать.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит.
Начинаем прибавлять уставку: 16.1, 16.4, 17, 18, 20, 22, 24 (опа! засветилось! ура!), 28, 30, 40, 60… Красота! Работает!
Наблюдаем за процессом — вышло примерно на 60, болтается чуток туда-сюда, но держит. Вроде, всё красиво. Выдыхаем, проверяем управление с ПК: задаём 600 градусов. И… Лампочка выключается. Как так? Уставка 600, текущая 60, а лампочка не горит?

Пока ждём и медленно осознаём, что мы явно напоролись на какой-то «Классический Косяк №2» ™ лампочка медленно разгорается, выходит на 100% мощности, и так и остаётся — 600-то градусов она выдать ну никак не может.

Возвращаемся снова к нашей разностной схеме. U(n) = U(n-1) + Kp*(dE + ...). К текущему расчетному значению воздействия прибавляется разность невязки помноженная на коэффициент пропорциональности. У нас была уставка 60, температура 60, то есть невязка нулевая. Выходная мощность так же была нулевая. И тут разом, скачком, уставку увеличили до 600 градусов. невязка резко стала 540 градусов, помножили еще и на коэффициент пропорциональности… и вылетели за разрядность хранения U(n). Не смейтесь, использование математики с фиксированной точки, вместо плавающей точки. При разнице в 540 градусов и работе через 1/16, при коэффициенте пропорциональности 20, получаем… 540*20*16=172800, а если у нас 16тиразрядный U(n), да еще и знаковый, то фактически, в результате вычисления мы получили A300h = −8960. Опачки. Вместо большого плюса — ощутимый такой минус.

Вывод №2: вычисления должны проводиться с корректной поддержкой переполнения. Переполнилось? Ограничь предельным числом, уж никак не заворачивать.

Итак, нарастили разрядность U(n), перетранслировали, зашили, запускаем. Лампочка еще не совсем остыла, там 80 градусов, уставка всё те же 600. Лампочка зажигается… и тухнет. Зажигается и тухнет. Как так? Уставка 600, лампочка 80 — и поддерживает вполне себе свои 80! Как так-то?! Явно у нас вылез Жучок №3.

И снова лирически-математическое отступление. Итак, есть наша разностная схема: U(n) = G(U(n-1), dE(n)). Еще раз: новое значение воздействия есть сумма прошлого воздействия и некого воздействия, зависящего от разности невязки в текущий момент и предыдущий. А что такое предыдущий момент? А какой момент предыдущий у предыдущего? Ну-ка, вспомнили школу. Доказательство по индукции. Если можно построить доказательство для K+1, считая что доказательство для K верно, И доказать отдельно что верно для K=0, тогда доказательство истинно. Итак, а как мы считаем U(0)?

Часто встречающееся решение: всё обнуляем, уставку считываем из флешпамяи уставки, ждём 1 цикл опроса, и считываем X(0). Вот, ноль готов, теперь работаем. И… И не правильно. Почему? Потому что рекурентная формула отталкивается от изменений в невязке. А проинициализировав нулём и загрузив текущие значения мы потеряли стартовые условия. Всё — вместо поддержания абсолютного значения температуры на уровне равном абсолютной уставке регулятор начинает держать температуру равную стартовой плюс разнице уставки. То есть было 80 градусов и уставка 200, включили прибор — он держет 80. Сменили уставку на 240 — он начал держать 120.

Правильная инициализация разностной схемы: обнулить _вообще всё_. То есть
X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
И на первом же цикле вычислений у нас как бы скачком появляются уставке и текущее значение:
X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 - 80 - 0) = 2400
Вот теперь схема работает правильно.

Вывод №3: корректно инициализируй стартовые условия.

Правильно ли? Hу-ка, ну-ка… Еще раз… Ставим уставку 20. Ждём охлаждения… Выключаем. Включаем. Итак, красота: текущая 20, уставка 20. Ставим скачком 600. Поехало греться. 100, 120… ставим уставку 20. Отключилось, пошло охлаждаться. Ждём чуток (120… 110… 100… 90… 80…) и ставим уставку 100. Поехало греться… 105 градусов, отключилось. Стоп. А почему оно держит 105? У нас же сейчас работает только пропорциональная составляющая. При правильной реализации из физического смысла процесса колебательный процесс не может держать уставку выше чем задано. Строго ниже. А держит на 5 градусов больше чем попросили. Это наблюдается Прикол №4.

Итак, вспоминаем что у нас было выше: Вывод№2: U(n) нельзя ограничивать. И Вывод№3: при переполнении ограничить всё-таки придётся. Да-да. Иначе «рабочая точка» смещается на ограниченный момент. Что же делать? Увеличить разрядость? Хорошо, если хватает вычислительной мощности. А надо ли? Собственно, что плохого, что у нас U(n) = 9999.99, а не 29999.99? В общем-то только то, что мы потеряли 20000. Но сейчас-то для работы нам так и так надо вваливать просто 100% мощности, правильно? Правильно. Значит, проблемы с ограничением в полку нет, до тех пор, пока мы не отходим от предела. Таким образом, в случае переполнения надо ставить флаг, и по достижении, например, половины диапазона (то есть как U(n) после 9999.9 опустилось ниже 5000.00), заново реинициализировать схему. То есть отбрасывать историю, сказать что n=0 и см. выше Вывод №3. Пытливый ум уже сообразил, что в случае полной схемы, когда все три компоненты не равны нулю, обнуляя в процессе итеративный процесс, мы в том числе обнуляем накопленный интеграл интегральной составляющей. Однако, в связи с тем, что обнуляем мы значительно заранее, он успеет подкопиться за время довырабатывания остатка. Да и не совсем корректно копить интеграл на «больших» перегонах, так как цель интегральной составляющей — «выбрать» невязку, которую не может отработать пропорциональная составляющая отдельно.

Вывод №4: если по какой-то причине U(n) было ограничено, схему следует переинициализировать как только создалось впечатление, что схема вернулась в нормальное состояние.

В следующем выпуске: а так ли надо реализовывать разностную схему? Подробная реализация прямой дискретной схемы, обладающей простыми и понятными настраиваемыми коэффициентами, с прямым физическим смыслом, которая без проблем вычисляет управляющее воздействие с частотой 25Гц на процессоре ADuC847 (быстрый 8-битный контроллер, с ядром 8051), оставляя еще море процессорного времени для других процессов.

(Картинки с изображением формул взяты из статьи ПИД-Регулятор в Wikipedia)

ПИД — регулятор. Основы автоматики на примере.

Всем привет. Рассмотрев в прошлой статье основу технологии построения веб-интерфейса, мы возьмем небольшую паузу с проектированием, и рассмотрим пару статей по ПИД–регулятору. Куда войдут основы автоматики, и на примере устройства синхронизации двигателей фрезерного станка на микроконтроллере, познакомимся с основными законами управления. А также рассчитаем основные коэффициенты законов для матмодели. В конце статьи выложен проект в Proteus на ATmega8.

 Но для начала «пробежимся» по основным понятиям, что б понимать о чем мы с Вами будем далее говорить. В проекте предполагается управлять двигателем, т.е. объектом. Что в свою очередь автоматика так и называет объект управления (ОУ). У него имеется три параметра:
1. Выходная величина y.
2. Входной задающий параметр u.
3. Входное возмущающее воздействие f.
На рисунке слева представлен общий вид ОУ с его параметрами. Справа наш пример представленный в протеусе в виде двигателя с энкодером, где входным задающим параметром является постоянное напряжение и в зависимости от его величины изменяется частота вращения двигателя. Выходным параметром является показания энкодера, а именно угол поворота (число импульсов за один оборот). Третий параметр — возмущающее воздействие — это воздействие со стороны внешней среды, которое нарушает правильное функционирование объекта, т.е. трение, нагрузка и т.д.

 

 

 

Для исключения последнего используется второй параметр, т.е. задающий. Техническое устройство, осуществляющее автоматическое управление называется управляющим устройством (УУ). А ОУ совместно с управляющим и задающим устройствами называют систему автоматического управления (САУ). Ниже структурная схема системы.

Здесь хочется сразу добавить, что ОУ может управляться по трем основным принципам:
1. Принцип разомкнутого управления – вырабатывается на основе заданного алгоритма и не контролируется другими факторами.
2. Принцип компенсации возмущений, где результат возмущения в виде корректива вносится в алгоритм управления.
3. Принцип управления по ошибке. Здесь коррективы вносятся в алгоритм управления по фактическому значению выходной величины.

Наш проект будет строится по последнему принципу управления – по ошибке. Ниже, слева структурная схема, а справа проект, где осуществляется управление по ошибке.

 

 

 

 

ЗУ — это у нас двигатель с энкодером (с левой стороны), с которого импульсы поступают в микроконтроллер. Где в свою очередь прописана матмодель ПИД-регулятора. Контроллер выступает в роли УУ. Далее ШИМ генерирует необходимый импульс и посылает его на вход второго двигателя с энкодером, который правее. (Мы с Вами уже рассматривали ШИМ-управление на AVR). Выход импульсов с которого, является выходной величиной и ошибкой в обратной связи y ос. Кнопки — это возмущающее воздействие, которыми мы произвольно добавляем импульсы ОУ. Где в свою очередь УУ должно быстро и плавно подрегулировать под угол поворота задающего устройства.

Далее САУ классифицируются по:
1. Алгоритму функционирования:
— системы стабилизации — поддержание регулируемого параметра на заданном уровне;
— программное управление – алгоритм задан в функции времени, где выходная величина изменяется во    времени по заданному закону;
— следящие системы  — алгоритм функционирования заранее не известен, где регулируемая величина должна воспроизводить изменение некоторой внешней величины;
— экстремальные системы — показатель качества или эффективности процесса может быть выражен в виде функции параметров системы, а сама функция имеет экстремум (максимум или минимум).
— системы оптимального управления — процесс управления ведется таким образом, что некоторая характеристика процесса была бы оптимальной;
— адаптивные системы – некоторые параметры ОУ и др. элементов системы могут изменяться.
Наш алгоритм это программное управление, где выходная величина будет результатом ПИД управления.
2. По виду дифференциальных уравнений, описываемых систему – линейные (статические характеристики всех элементов являются прямолинейными) и нелинейные (статическая характеристика является нелинейной).
3. По характеру сигналов в основных элементах —  непрерывные и дискретные(в последних непрерывный входной сигнал преобразуется на выходе в последовательность импульсов).

Наш проект нелинейный и сигналы дискретные. И последнее, рассмотрим типовые законы управления, определяющие алгоритм управления в функции от ошибки управления. Под законом регулирования понимают алгоритм, в соответствии с которым управляющее устройство формирует воздействие, подаваемое на вход ОУ.  Законы управления описываются передаточными функциями, которые являются одним из способов математического описания динамической системы. Вид передаточной функции управляющего устройства определяет закон управления. Различают пять основных законов управления: пропорциональный (П), интегральный (И), пропорционально –интегральный (ПИ), пропорционально-дифференциальный (ПД), пропорционально — интегрально – дифференциальный (ПИД).

Рассмотрим каждый закон в отдельности на примере устройства синхронизации. Итак, исходные данные:

Соберем пример в Proteus. Возьмем два движка с инкрементальными энкодерами, микроконтроллер, два счетчика импульсов, а также подключим осциллограф и ЖК индикатор для отображения рассогласования (ошибки). Рассмотрение датчиков угла поворота (энкодера) выходит за пределы статьи, единственное, что нам надо знать, они предназначены для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота. Выше был представлен рисунок нашего проекта в Proteus. Ниже на рисунке пример настройки мотора с энкодером:

Где в свойствах мотора выставим:
— минимальную массу ротора EffectiveMass= 0,01;
— нагрузка ротора Load/MaxTorque % = 1, чтобы он по инерции не крутился;
— обороты ZeroLoad RPM=20;
— количество импульсов на оборот PulsesperRevolution=24.
Как видите в протеусе отдельного энкодера нет, только с двигателем. Кратко о его подключении. Один конец двигателя на землю, на второй напряжение от -12 или +12 В. И три вывода энкодера. Мы используем один как на рисунке выше. Приведенные параметры являются настроечными параметрами от которых будет зависеть динамика привода, т.е. его поведение.

П — регулятор. Одно из простых устройств и алгоритмов управления, в обратной связи, которое формирует управляющий сигнал. Выдает выходной сигнал u (t), пропорциональный входному (ошибке регулирования) e (t), с коэффициентом пропорциональности К, который вырабатывается пропорциональной частью П-регулятора в противодейтвие отклонению реглируемой величины от данного значения, в данный момент времени.

u (t)=K_р*e (t), где K_р — коэффициент усиления регулятора.

Чем больше отклонение, тем больше выход именно по данному значению. Т.е. статическая ошибка равна отклонению регулируемой величины. Здесь присутствует вероятность, что система никогда не стабилизируется на заданном значении. Увеличение коэффициента усиления увеличивает разницу между входом и выходом, при этом уменьшается статическая ошибка. Но рост этого коэффициента может привести к автоколебаниям в системе, а дальнейшее его увеличение приведет к потере устойчивости.

Обычно на практике усилительные свойства П-регулятора характеризуют следующими величинами:
— предел пропорциональности d=1/K_р — величина, обратная K_р
— предел пропорциональности, выраженный в процентах D=d*100%=100%/K_р. Показывает, на сколько процентов от своего максимального значения должен изменится входной сигнал, чтобы выходной изменился на 100%.

Автоколеба́ния — это незатухающие колебания в диссипативной ( устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне) динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, т. е. непериодического внешнего воздействия.
На рисунке ниже слева нормальный процесс П-регулирования, где видно, что линейность  графика прямо пропорционально уменьшению ошибки. Справа, процесс автоколебаний в системе при большом коэффициенте.

 

 

 

 

 

 

П-регулятор находит свое применение в тех же процессах, где не требуется точного поддержания заданного значения, описанных ранее, то есть в контролируемом процессе будет присутствовать статическая ошибка. Возникает данная ошибка из-за того, что выходной сигнал слишком мал для оказания существенного воздействия на поддержание системы на заданном уровне. Вполне допускается, что регулятор выведет требуемое значение, но при возникновении возмущающих воздействий, регулятор не сможет вернуть заданное значение, пока рассогласование не станет достаточно велико, чтобы выходной сигнал смог оказать достаточное воздействие. Для нашего примера такой закон не подходит. Идем далее.

И-регулятор. Что значит интегральное управление? А то, что устройство вырабатывает сигнал (u (t)), пропорциональный интегралу от ошибки регулирования (e (t)). Система при таком законе астатическая, т.е.возмущение происходит на том участке системы, который находится за интегрирующим звеном. Но при этом динамические свойства системы с И-законом обычно хуже чем у системы П-управления. Ниже представлен закон И-регулятора.

где K0 — коэффициент усиления регулятора. Скорость изменения выхода  И-регулятора пропорциональна ошибке регулирования. Обычно на практике усилительные свойства И-регулятора характеризуют временем изодрома.

Время изодрома Т_и=1/K₀ — величина, обратная K_0. Также показывает за какое время выход регулятора изменится на 100% (регулирующий орган переместится из одного крайнего положения в другое) при скачкообразном изменении входного сигнала на 100%. Таким образом Т_и характеризует быстродействие регулятора. С уменьшением T растет колебательность переходного процесса. При слишком малых значениях T система регулирования может перейти в неустойчивое состояние. Ниже на рисунке слева устойчивое состояние, справа — неустойчивое состояние.

 

 

 

 

 

 

 

В системе регулирования с И-регулятором обычно отсутствует статическая ошибка регулирования. Как правило И-регулятор не используется самостоятельно, а в составе ПИ- или ПИД- регуляторов.

ПИ-регулятор. Изодромное управление. Управляющее устройство вырабатывает суму двух сигналов — пропорционального ошибке и пропорционального интегралу от ошибки. Выходной сигнал ПИ-регулятора ( u (t) ) зависит и от ошибки регулирования ( e (t) ), и от интеграла от этой ошибки.
 
K₁ — коэффициент усиления пропорциональной части,
K₀ — коэффициент усиления интегральной части

Так как  ПИ-регулятор можно рассматривать как два регулятора, соединенные параллельно, то усилительные свойства ПИ-регулятора характеризуют два параметра:
1) предел пропорциональности d=1/K₁ — величина, обратная K₁
2) время изодрома Т_и=1/K₀ — величина, обратная K_{0 .}

Динамические свойства системы с ПИ-регулятором лучше, чем с  И-законом. Изодромная система в переходном режиме приближается к системе с пропорциональным управлением. А  в установившемся режиме подобна системе с интегральным управлением.  Чем больше коэффициент пропорциональности, тем меньше выходная мощность при одной и той же ошибке регулирования, чем больше постоянная времени интегрирования, тем медленнее накапливается интегральная составляющая. ПИ регулирование обеспечивает нулевую ошибку регулирования и нечувствительно к помехам измерительного канала. Ошибка регулирования (статическая) исключается за счет интегрального звена, которое образуется  путем  постоянного  суммирования  ε  за  определенный  промежуток  времени и формирования сигнала управления, пропорционального полученной величине.

Недостатком ПИ регулирования является медленная реакция на возмущающие воздействия. Для настройки ПИ регулятора следует сначала установить постоянную времени интегрирования равный нулю, а коэффициент пропорциональности — максимальным. Затем как при настройке пропорционального регулятора, уменьшением коэффициента пропорциональности нужно добиться появления в системе незатухающих колебаний. Близкое к оптимальному значение коэффициента пропорциональности будет в два раза больше того, при котором возникли колебания, а близкое к оптимальному значение постоянной времени интегрирования — на 20% меньше периода колебаний. Оптимальным является переходной процесс с 20% перерегулированием.

ПД-регулятор. Если нагрузка объекта изменяется часто и резко, и при этом объект имеет существенное запаздывание, то ПИ-регулятор дает неудовлетворительное качество регулирования. Тогда целесообразно в закон регулирования вводить дифференцирующую составляющую, т.е. воздействовать на регулирующий орган дополнительно по величине первой производной от изменения регулируемого параметра. Cигнал ПД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ) и от производной от этой ошибки (от скорости изменения ошибки).

ПД-регулятор характеризуют два параметра:

1. Предел пропорциональности d=1/K1 — величина обратная К1.
2. Постоянная времени дифференцирования (время предварения) Тд=K2. Это интервал времени между моментами достижения регулирующим органом одинакового положения при наличии дифференциальной составляющей и без нее. Параметр настройки дифференциальной составляющей. За счет дифференциальной составляющей упреждается перемещение регулирующего органа. 

Дифференцирующее звено вычисляет скорость изменения ошибки, т.е. прогнозирует направление и величину изменения ошибки. Если она положительна, то ошибка растет и дифференцирующая часть вместе с пропорциональной увеличивает воздействие регулятора на объект. Если отрицательна — уменьшается воздействие на объект. Эта система регулирования имеет статическую ошибку регулирования, но быстродействие у нее выше, чем П- , И- , Пи-регуляторы. В начале переходного процесса ПД-регулятор имеет высокое усиление и, следовательно, точность, а в установившемся режиме он вырождается в П-регулятор со свойственной ему статической ошибкой. Если статическую ошибку скомпенсировать, как это делается в П-регуляторах, то возрастет ошибка в начале переходного процесса. Таким образом, ПД-регулятор по своим потребительским свойствам оказывается хуже П-регулятора, поэтому на практике он используется крайне редко. П-звено имеет положительное свойство — вносит в контур регулирования положительный фазовый сдвиг, что повышает запас устойчивости системы при малом времени предварения. Однако с увеличением этого времени растет усиление регулятора на высоких частотах, что приводит к режиму автоколебаний. Чем больше время дифференцирования, тем больше скачок в перемещении регулирующего органа.

ПИД-регулятор. Это сумма трех регуляторов П, И и Д (Пропорционально-интегрально-дифференцирующий). Выходной сигнал ПИД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ), от интеграла от этой ошибки и от производной от этой ошибки.

 Усилительные свойства характеризуют три параметра:

1. Предел пропорциональности d=1/K1.
2. Время изодрома Ти=1/K0.
3. Время предварения  Тд=K2.

Системы регулирования с ПИД-регуляторами сочетают в себе достоинства П- , И- , и ПД- регуляторов. В таких системах отсутствует статическая ошибка и они обладают высоким быстродействием.

Ниже выложен проект в Proteus на ATmega8. Где представлена выше описанная модель ПИД — регулятора.

Синхронизация двигателей станка ( Скачали: 527 чел. ) 

В следующей статье рассмотрим расчет основных коэффициентов законов регулирования для нашего проекта, а именно синхронизации двигателей станка. Написание матмодели для микроконтроллера и существующие варианты. А также этапы проектирования: от замысла до платы. На этом мы сегодня и остановимся. Всем пока.

Просмотрено 16210 раз.

Принцип работы ПИД-регуляторов

Опубликовано 24.05.2016

Принцип работы

Регуляторы процесса

Регуляторы процесса (Process Controllers) – это параметрируемые цифровые контроллеры со встроенным набором стандартных функций для регулирования технологических переменных (температуры, давления и т.п.).

В качестве сигналов задания (Reference) могут использоваться как фиксированные уставки (Fixed Setpoints), так и внешние (External).

Аналоговые входы используются для подключения датчиков обратной связи (термометров сопротивления, термопар, манометров и т.п.).

Дискретные входы используются для задания фиксированных уставок и переключения между режимами.

Дискретные выходы используются для сигнализации: готовности, аварий, состояния.

Релейные выходы используются для дискретного управления, а аналоговые выходы – для непрерывного управления.

Дискретное управление

• 2-х позиционный регулятор использует только 2 состояния:
• включено (открыто)
• выключено (закрыто)
Пример: управление нагреванием или охлаждением.
• 3-х позиционный регулятор использует 3 состояния:
• выключено
• вращение по часовой стрелке
• вращение против часовой стрелки (реверс)
Пример: управление реверсивным электродвигателем.
• 5-и позиционный регулятор использует 5 состояний:
• выключено
• вращение на первой скорости по часовой стрелке
• вращение на второй скорости по часовой стрелке
• вращение на первой скорости против часовой стрелки
• вращение на второй скорости против часовой стрелки
Пример: управление 2-скоростным реверсивным двигателем.

Непрерывное управление

Для непрерывного управления используются ПИД-регуляторы. Возможна реализация каскадного (подчинённого) управления.

Замкнутая система управления

Переходный процесс

Переходный процесс – это реакция системы на внешнее воздействие (задание, возмущение).

Неустойчивый (расходящийся) переходный процесс

Устойчивый (сходящийся) переходный процесс

Колебательный	Апериодический	Монотонный

ПИД-регулятор

С помощью настройки ПИД-регулятора (PID-controller) мы можем скорректировать переходный процесс так, как нам нужно для решения своей задачи.

Х_зад – заданное (желаемое) значение выходной переменной
X_max – верхний допустимый предел выходной переменной
X_min – нижний допустимый предел выходной переменной
Т – период колебаний
Т_н – время нарастания
Т_р – время переходного процесса (последняя точка пересечения кривой с X_min или X_max)
А₁ – первое перерегулирование
А₂ – второе перерегулирование
d=А₁/A₂ — степень (декремент) затухания переходного процесса (отношение первого перерегулирования ко второму)

Рассогласование, перерегулирование, время нарастания, время переходного процесса, степень затухания характеризуют качество регулирования.

Пример

ПИД-регулятор открывает и закрывает регулирующий вентиль на горячей трубе так, чтобы из крана текла вода с температурой +40°С с погрешностью плюс-минус 2 градуса. Регулятор вычисляет рассогласование (ошибку) — отклонение реальной температуры (например, +20°С) от заданного значения (+40°С) и решает – когда и насколько необходимо приоткрыть горячий вентиль, чтобы температура повысилась на 20С. Реальную (фактическую) температуру регулятор узнаёт с помощью датчика температуры (обратная связь), а заданную температуру (уставку) ему сообщает оператор, например, набирая число «40» на своём ПК.

Чтобы настроить ПИД-регулятор, необходимо подобрать правильную комбинацию трёх коэффициентов:

• Пропорционального – K_p
• Интегрального – K_i
• Дифференциального – K_d

Могут использоваться и более простые — П и ПИ-регуляторы.

Формула ПИД-регулятора

где e(t) — ошибка (рассогласование), u(t) — выходной сигнал регулятора (управляющее воздействие).

Чем больше Пропорциональный коэффициент, тем выше быстродействие, но меньше запас устойчивости. Но! простой П-регулятор не может полностью отработать рассогласование, т.е. всегда работает с ошибкой.

ПИ-регулятор позволяет избавиться от статической (установившейся) ошибки, но, чем больше Интегральный коэффициент, тем больше перерегулирование (динамическая ошибка).

ПИД-регулятор позволяет нам уменьшить перерегулирование, но, чем больше Дифференциальный коэффициент, тем больше погрешность из-за влияния шумов.

Если шумы идут по каналу обратной связи, то мы можем их отфильтровать с помощью фильтра низкой частоты, но чем больше постоянная этого фильтра, тем медленнее регулятор будет отрабатывать возмущения.

Настройка ПИД-регулятора по методу Циглера-Николса

Циглер и Николс предложили свой вариант быстрой настройки ПИД-регулятора для периодического переходного процесса, в котором затухание примерно равно 4.

• Обнуляем K_i и K_d
• Постепенно увеличиваем Kp до критического значения K_c, при котором возникают автоколебания
• Измеряем период автоколебаний Т
• Вычисляем значения K_p, K_i и K_d по разным формулам для разных регуляторов:
• для П-регулятора: K_p=0,50*K_c
• для ПИ-регулятора: K_p=0,45*K_c, K_i=1,2*K_p/T
• для ПИД-регулятора: K_p=0,60*K_c, K_i=2,0*K_p/T, K_d=K_p*T/8

Каскадный регулятор (подчинённое управление)

Продолжение примера

Теперь нам захотелось добавить комфорта и сделать так, чтобы уставка задания температуры воды менялась в зависимости от температуры воздуха на улице (на улице мороз – вода горячая, на улице жара – вода прохладная). Можно установить ещё один регулятор комфортной температуры, который по показаниям термометра узнаёт фактическую температура наружного воздуха и решает, что комфортная температура воды должна быть, например, +40°С, поэтому он выдаёт задание регулятору температуры воды – поддерживать температуру на уровне +40С (см. пример выше). Здесь мы имеем каскадное регулирование: контур регулирования температуры воды подчинён контуру регулирования комфортной температуры воды.

С помощью регуляторов процесса мы можем реализовать и более сложные связи. Например, поддерживать постоянный расход и температуру воды, независимо от давления и температуры горячего и холодного трубопроводов.

Упреждающее регулирование (Feedforward Control)

Не всегда простой ПИД-регулятор в системе с обратной связью может обеспечить требуемое быстродействие из-за возникновения нежелательных колебаний или недопустимо большого перерегулирования. Для улучшения характеристик регулирования применяют комбинированное управление – с обратной связью (closed-loop) и без обратной связи (open-loop). К управляющему воздействию (выходу регулятора) добавляется сигнал упреждающего воздействия, который не зависит от рассогласования, а значит, не может вызвать автоколебания в системе.

Продолжение примера

Если мы доверяем прогнозу погоды, то вместо каскадного управления мы можем реализовать упреждающее регулирование без измерения уличной температуры: читаем прогноз на завтра, задаём уставку +40°С по таймеру времени на завтра на 7 утра.

Если измерить возмущение, то можно подать упреждающее воздействие, которое компенсирует влияние этого возмущения на процесс до того, как начнёт изменяться регулируемый параметр.

Симуляция ПИД-регулятора температуры / Хабр

Поискал я статьи на данном ресурсе на тему ПИД-регуляторов. Много статей. И с объяснением принципов работы таких регуляторов. И с алгоритмами подбора параметров. И с реализацией на конкретных железках и программах. Не увидел одного — симуляции ПИД-регуляторов на моделях, с тем, чтобы пользователь без использования без всякого железа мог «пощупать» работу ПИД-регулятора.

Для этого создана матмодель нагревательного элемента с датчиком температуры и ПИД-регулятором (разумеется, с кучей упрощений, но без ущерба для реалистичности). Реализовано это на обычном Excel. С тем, чтобы любой пользователь мог сам «покрутить» виртуальные параметры, и посмотреть, что из этого выходит. Собственно, я эту модель в своё время и сделал как раз для того, чтобы «потрогать» своими руками процесс ПИД-регулирования.

Сама модель имеет следующие параметры:

• Кf инерционности нагреваемого тела (масса, уд. теплоёмкость, изоляция)
• Температура окружающей среды °С
• Начальная температура тела °С

ПИД-регулятор имеет параметры:

• Целевая температура °С
• Коэфф. пропорционального воздействия
• Коэфф. дифференциального воздействия
• Коэфф. интегрального воздействия
• Максимальное значение управляющего воздействия
• Общий коэффициент усиления (если 0, то регулятор и нагреватель не работают)

Дальше много картинок.

1. Сначала выключим ПИД-регулирование и убедимся, что модель адекватная.

Устанавливаем равную температуру тела и окружающей среды и убеждаемся на графике, что температура стабильна:

Теперь устанавливаем температуру тела выше температуры окружающей среды, график перестроился и видим, что температура тела по экспоненциальному закону стремится к температуре окружающей среды.

То же самое, но теперь температура тела ниже температуры окружающей среды.

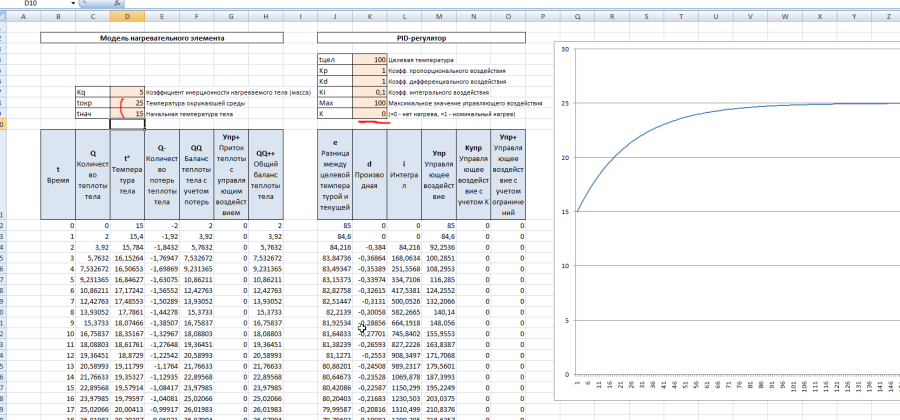
Уменьшаем коэффициент инерционности, и видим, что температура тела быстрее стремится к окружающей среде.

Увеличиваем коэффициент инерционности, и видим, что температура тела медленнее стремится к окружающей среде.

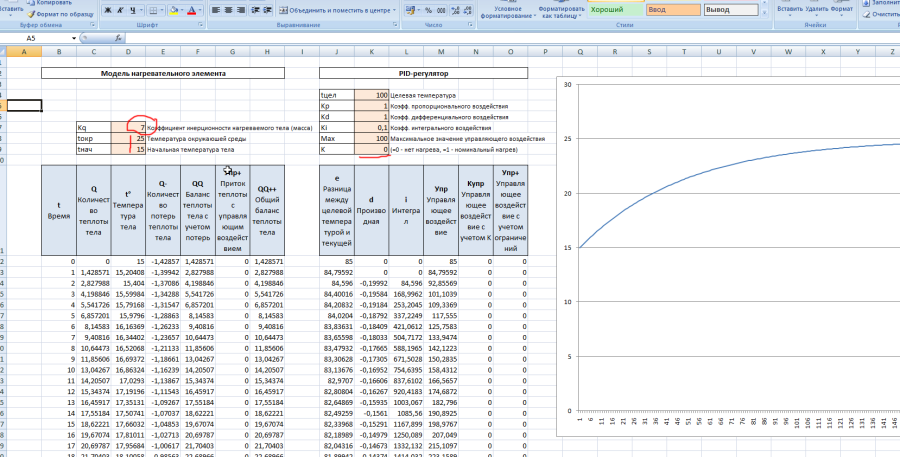
Теперь включаем нагрев (но не ПИД-регулятор!). Для этого в колонке управления «включаем» 2 раза «нагрев» — с 0 по 2 единицу времени на «мощность» =20, и с 11 по 12 единицу времени на «мощность» =10. На графике наблюдаем адекватную реакцию.

Теперь «включаем» постоянный «нагрев» на «мощность» 10. Видим, что температура тела растёт, но до определенного предела — «мощности» не хватает.

2. Теперь «включим» ПИД-регулятор, и посмотрим, как он будет регулировать температуру.

Установим целевую температуру в 100°С и Kp=1,Kd=1,Ki=0.1

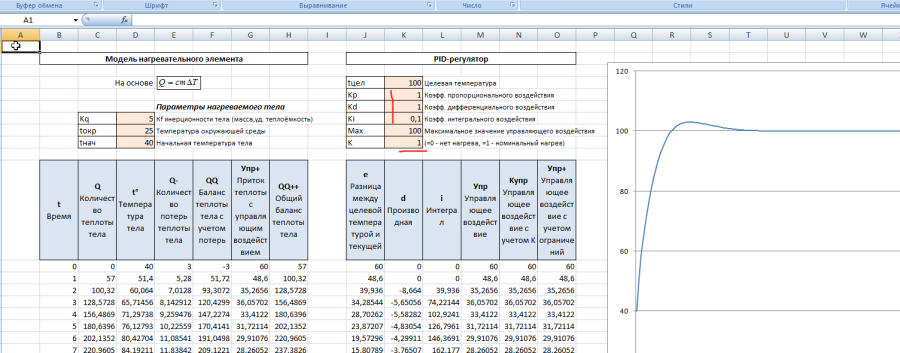
Увеличим Ki до 1, и увидим, что это не совсем полезно в данном случае.

Теперь уберем интегральную составляющую Ki и посмотрим — теперь регулировка не дотягивает до 100 градусов — мало «мощности» без интегральной составляющей.

Увеличим K и/или Kp — теперь «мощности» хватило, но без интегральной составляющей возникли высокочастотные колебания.

Ну и так далее.

Ссылка на файл. Кому интересно — поиграйтесь.

ПИД-регулятор. Описание и принцип работы.

Сегодняшняя статья будет посвящена такой замечательной вещи, как ПИД-регулятор. По определению, пропорционально-интегрально-дифференциальный регулятор — устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра. Чаще всего можно встретить примеры, где ПИД-регулятор используется для регулировки температуры, и, на мой взгляд, этот пример прекрасно подходит для изучения теории и понимания принципа работы регулятора. Поэтому именно задачу регулировки температуры и будем сегодня рассматривать.

Итак, что у нас имеется?

Во-первых, объект, температуру которого необходимо поддерживать на заданном уровне, кроме того, эту температуру необходимо регулировать извне. Во-вторых, наше устройство на базе микроконтроллера, с помощью которого мы и будем решать поставленную задачу. Кроме того, у нас есть измеритель температуры (он сообщит контроллеру текущую температуру) и какое-нибудь устройство для управления мощностью нагревателя. Ну и поскольку необходимо как-то задавать температуру, подключим микроконтроллер к ПК.

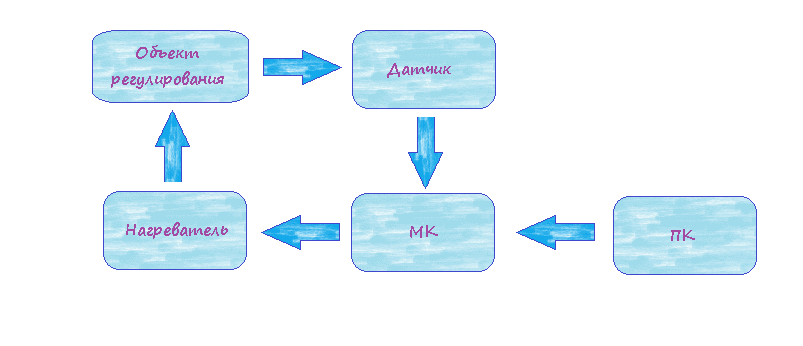
Таким образом, у нас есть входные данные:

• текущая температура,
• температура, до которой необходимо нагреть/остудить объект.

А на выходе мы должны получить значение мощности, которое необходимо передать на нагревательный элемент. И для такой задачи, да и вообще любой похожей задачи, отличным решением будет использование  пропорционально-интегрально-дифференциального регулятора 🙂

Начнем с пропорциональной составляющей. Здесь все просто, берем значение нужной нам температуры (уставку) и вычитаем из него значение текущей температуры. Получаем рассогласование (невязку). Умножаем полученную невязку на коэффициент и получаем значение мощности, которое и передаем на нагреватель. Вот и все!

Но при использовании только пропорциональной составляющей есть два больших минуса. Во-первых, эффект от нашего воздействия наступает не моментально, а с запаздыванием. И, во-вторых, пропорциональная составляющая никак не учитывает воздействие окружающей среды на объект.

Например, когда мы добились того, чтобы температуры объекта была равна нужному нам значению, невязка стала равна нулю. А вместе с ней и выдаваемая мощность стала нулевой. Но температура не может просто так оставаться постоянной, поскольку происходит теплообмен с окружающей средой и объект охлаждается. Таким образом, при использовании только пропорциональной составляющей температура будет колебаться около нужного нам значения.

Давайте разбираться, как ПИД-регулятор решает две выявленные проблемы.

Для решения первой используется дифференциальная составляющая. Она противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Каким образом? Сейчас разберемся!

Итак, пусть у нас текущая температура меньше нужного нам значения. Пропорциональная составляющая начинает выдавать мощность и нагревать объект. Дифференциальная составляющая вносит свой вклад в мощность и представляет из себя производную невязки, взятую также с определенным коэффициентом. Температура растет и приближается к нужному значению, а следовательно невязка в предыдущий момент больше текущего значения невязки, а производная отрицательная. Таким образом, дифференциальная составляющая начинает постепенно снижать мощность до того, как температура достигла необходимого значения.

С этим вроде разобрались, вспоминаем про вторую проблему регулятора 🙂

А с ней нам поможет справиться интегральная составляющая. Как нам в программе получить интеграл? А легко – просто суммированием (накоплением) значений невязки, на то он и интеграл! Возвращаемся к нашему примеру. Температура ниже значения уставки, начинаем подогревать. Пока мы нагреваем, значение невязки положительное и накапливается в интегральной составляющей. Когда температура “дошла” до нужного нам значения, пропорциональная и дифференциальная составляющая стали равны нулю, а интегральная перестала изменяться, но ее значение не стало равным нулю.

Таким образом, благодаря накопленному интегралу мы продолжаем выдавать мощность и нагреватель поддерживает нужную нам температуру, не давая объекту охлаждаться. Вот так вот просто и эффективно 🙂

В итоге мы получаем следующую формулу ПИД-регулятора:

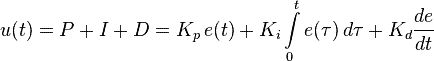
Тут  u(t) – искомое выходное воздействие, а e(t) – значение невязки. Частенько формулу преображают к следующему виду, но суть от этого не меняется:

Пожалуй, на этом закончим, разобрались мы сегодня как работает ПИД-регулятор, а в ближайшее время разберемся еще и как произвести настройку коэффициентов ПИД-регулятора!

ПИД-регулятор

— Большая химическая энциклопедия

ПИД-регулятор классический ПИД-регулятор (5.1) с прямой компенсацией заданной температуры реактора (т.е. ypdes добавляется к управляющему входу). [Pg.109]

Hagglund, T. K. J. Astrom (1985), Метод и устройство для настройки PID-регулятора, Патент США 4549123. [Pg.219]

Современный контроллер DDC имеет только функцию управления PID. Контроллеры ПЛК, используемые в технологических установках, могут содержать более сложные функции регулирования, например, нечеткую или автоматическую настройку функций ПИД.Большинство контроллеров DDC самодостаточны и не зависят от контроллеров или компьютерных программ, которые используются для настройки системы. [Pg.776]

Здесь мы должны проводить различие между электрическими контроллерами (например, ПИД-регуляторами) с пропорциональным клапаном в качестве привода и контроллерами с механической диафрагмой. В системе регулирования с электрическими контроллерами координация между контроллером и приводом (пьезоэлектрический впускной клапан для газа, впускной клапан A / i с моторным приводом, дроссельная заслонка, дроссельная заслонка) затруднена из-за очень разных граничных условий (объем емкости , эффективная скорость откачки в емкости, диапазон регулирования давления).Такие схемы управления имеют тенденцию легко вибрировать при возникновении сбоев процесса. Указать общепринятые стандартные значения практически невозможно. [Стр.91]

Даже с усовершенствованным ПИД-управлением регулирование никогда не бывает идеальным. Система нуждается в разнице между Cl и CO, чтобы реагировать, и при небольшом усилении эта разница может быть большой, поэтому, по крайней мере, временно, контроль будет частичным. Более того, попытка компенсировать это, например, увеличив A3 в формуле. (5), может привести к неустойчивости, колебаниям и т. Д.[Стр.150]

Таким образом, контур управления, показанный на рис. 5.28, был разработан для решения задачи управления симметрией [121]. Два дополнительных контура ПИД-регулирования используются для контроля однородности парциального давления реактивного газа благодаря соответствующему регулированию тройного входа газа (верх / центр / низ). … [Pg.223]

Регулировка теплообменников и нагревательных рубашек осуществляется пневматическими регулирующими клапанами. Это реализуется последовательными ПИД-регуляторами с учетом температуры масла, а также температуры газовой среды.[Pg.626]

Отклик системы с (a) пропорциональным + производным (PD) управлением и (6) пропорциональным + интегральным + производным (PID) управлением, когда коэффициент усиления составляет 15 процентов от критического усиления. Часть (c) показывает отклик с ПИД-регулированием, когда усиление составляет 50 процентов от критического усиления, практический предел для хорошего регулирования. Сравните эти ответы с показанными на рис. 10 для простого пропорционального (P) управления. [Стр.580]

Flygare et al. (1990) продемонстрировали ЭТ-мониторинг процедуры аффинной адсорбции.Лактатдегидрогеназу (ЛДГ) выделяли из неочищенного раствора путем аффинного связывания с гелем N6- (6-аминогексил) -АМР-сефарозы. Сигнал активности LDH от ET использовался в ПИД-регуляторе для регулирования добавления … [Pg.43]

Основным источником тепла является горячая вода. Горячая вода нагревается путем прямого впрыска пара в водонагреватель. Для контроля температуры продукта используются три ПИД-регулятора. Первый контур управления регулирует … [Pg.109]

Процесс пастеризации HTST (Рисунок 5.5) подробно описан в разделе 5.3. В качестве переменных здесь используются четыре измерения температуры (° C) и два выхода ПИД-регулятора (мА). Температура горячей воды, температура сырого продукта на выходе из подогревателя, температура на входе в трубку выдержки пастеризованного продукта и температура на выходе трубки выдержки пастеризованного продукта являются выходными переменными процесса (переменные 1-4, соответственно). Входными переменными процесса являются выход ПИД-регулятора на паровой клапан (переменная 5), который регулирует температуру продукта на входе в сборную трубу, и выход ПИД-регулятора для горячей воды подогревателя… [Pg.167]

Платиновые термометры сопротивления контролируют температуру, а трехчленный настраиваемый ПИД-регулятор, связанный с ПК через RS232, стабилизирует значение на заданном значении с точностью не менее 0,1 ° C, регулируя вторичную теплопередачу. Заданное значение температуры можно запрограммировать, чтобы обеспечить возможность точного термоциклирования, или ввести вручную для ступенчатого изменения. Рабочий диапазон температур составляет 5 ° C с температурным откликом 0,2 ° C / с. [Pg.703]

---

.

Что такое ПИД-регулятор? Изучите методы работы, структуры и настройки ПИД-регулятора

Перед тем, как объяснять ПИД-регулятор , давайте рассмотрим систему управления. Есть два типа систем; система разомкнутого цикла и система замкнутого цикла. Система разомкнутого контура также известна как неуправляемая система и система замкнутого контура известна как управляемая система . В системе с разомкнутым контуром выход не управляется, потому что в этой системе нет обратной связи, а в системе с замкнутым контуром выход управляется с помощью контроллера, и для этой системы требуется один или несколько путей обратной связи.Система разомкнутого контура очень проста, но бесполезна в приложениях промышленного управления, поскольку эта система неуправляема. Система с замкнутым контуром сложна, но наиболее полезна для промышленного применения, поскольку в этой системе выходной сигнал может быть стабильным на желаемом значении, PID является примером системы с замкнутым контуром . Блок-схема этой системы показана на рисунке 1 ниже.

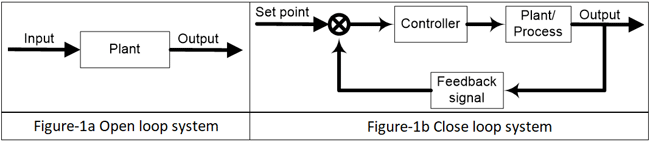
Система замкнутого контура также известна как система управления с обратной связью , и этот тип системы используется для разработки автоматически стабильной системы с желаемым выходом или заданием.По этой причине он генерирует сигнал ошибки. Сигнал ошибки e (t) — это разница между выходным сигналом y (t) и опорным сигналом u (t) . Когда эта ошибка равна нулю, это означает, что достигнут желаемый выход, и в этом состоянии выходной сигнал такой же, как опорный сигнал.

Например, , сушилка работает несколько раз, что является предварительно установленным значением. Когда сушилка включена, запускается таймер, и он будет работать до тех пор, пока таймер не закончится и не выдаст выход (сухая ткань).Это простая система с разомкнутым контуром, в которой выходной сигнал не требуется для управления и не требуется никакой обратной связи. Если в этой системе мы использовали датчик влажности, который обеспечивает обратную связь, сравнивает его с уставкой и генерирует ошибку. Сушилка работает, пока эта ошибка не станет нулевой. Это означает, что когда влажность ткани равна заданному значению, сушилка перестанет работать. В системе с открытым контуром сушилка будет работать в течение фиксированного времени независимо от того, сухая или влажная одежда. Но в системе с замкнутым контуром сушилка не будет работать в течение фиксированного времени, она будет работать, пока одежда не высохнет.Это преимущество замкнутой системы и использования контроллера.

ПИД-регулятор и его работа:

Так что же такое ПИД-регулятор? ПИД-регулятор является общепринятым и наиболее часто используемым регулятором в промышленных приложениях, поскольку ПИД-регулятор прост, обеспечивает хорошую стабильность и быстрый отклик. PID означает пропорциональный, интегральный, производный . В каждом приложении коэффициент этих трех действий варьируется для получения оптимального отклика и контроля.Вход контроллера — это сигнал ошибки, а выходной сигнал передается в установку / процесс. Выходной сигнал контроллера формируется таким образом, чтобы выходной сигнал установки пытался достичь желаемого значения.

ПИД-регулятор — это система с замкнутым контуром , которая имеет систему управления с обратной связью и сравнивает переменную процесса (переменную обратной связи) с заданным значением, генерирует сигнал ошибки и в соответствии с этим регулирует выходной сигнал системы. Этот процесс продолжается до тех пор, пока ошибка не станет равной нулю или значение переменной процесса не станет равным заданному значению.

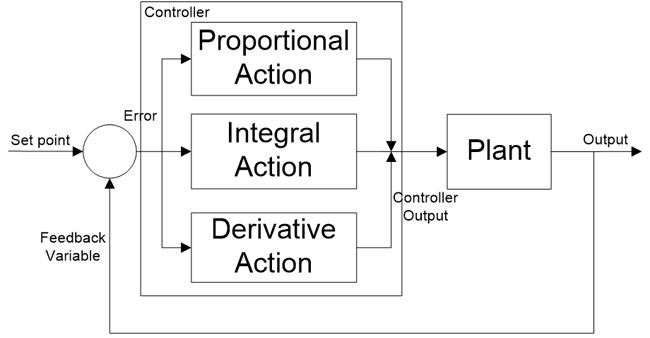
* Мы узнаем о пропорциональных, интегральных и производных действиях позже в этой статье.

ПИД-регулятор дает лучшие результаты, чем двухпозиционный регулятор . В контроллере ВКЛ / ВЫКЛ доступны только два состояния для управления системой. Он может быть включен или выключен. Он будет включаться, когда значение процесса меньше заданного значения, и выключится, если значение процесса больше заданного значения. В этом контроллере выходной сигнал никогда не будет стабильным, он всегда будет колебаться около заданного значения.Но ПИД-регулятор более стабилен и точен по сравнению с регулятором ВКЛ / ВЫКЛ.

ПИД-регулятор представляет собой комбинацию трех терминов; Пропорциональные, интегральные и производные . Давайте разберемся в этих трех терминах по отдельности.

Режимы управления ПИД:

Пропорциональный (P) ответ:

Член «P» пропорционален фактическому значению ошибки. Если ошибка велика, выходной сигнал управления также большой, а если ошибка мала, выходной сигнал управления также мал, но коэффициент усиления (K _p ) равен

Также с учетом.Скорость отклика также прямо пропорциональна коэффициенту пропорционального усиления (K _p ) . Таким образом, скорость отклика увеличивается за счет увеличения значения K _p , но если K _p увеличивается за пределы нормального диапазона, переменная процесса начинает колебаться с высокой скоростью и делает систему нестабильной.

у (т) ∝ е (т)
y (t) = k  i  * e (t) 

Где K _p — коэффициент пропорционального усиления.

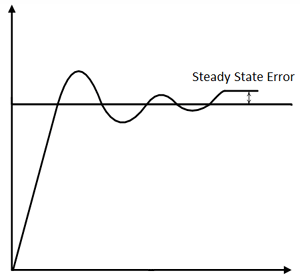
Здесь результирующая ошибка умножается на коэффициент усиления пропорциональности (константа пропорциональности), как показано в уравнении выше.Если в это время используется только P-регулятор, он требует ручного сброса, потому что он поддерживает ошибку устойчивого состояния (смещение).

Интегральный (I) отклик:

Встроенный контроллер обычно используется для уменьшения ошибки установившегося состояния. Член «I» интегрируется (по времени) с фактическим значением ошибки . Из-за интеграции очень малое значение ошибки, приводит к очень высокому интегральному отклику. Действие встроенного контроллера продолжает изменяться, пока ошибка не станет равной нулю.

у (т) ∝ ∫ е (т)
y (t) = k  i  ∫ e (t) 

Где K _i — коэффициент пропорционального усиления.

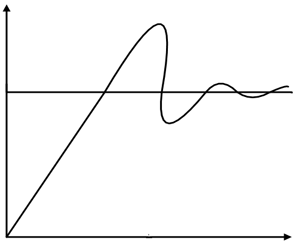
Интегральное усиление обратно пропорционально скорости отклика, увеличивая k _и , уменьшая скорость отклика. Пропорциональные и интегральные регуляторы используются вместе (ПИ-регулятор) для обеспечения хорошей скорости отклика и устойчивого состояния.

Ответ на производную (D):

Производный контроллер используется с комбинацией PD или PID.Он никогда не используется отдельно, потому что, если ошибка постоянна (не равна нулю), выходной сигнал контроллера будет нулевым. В этой ситуации контроллер ведёт себя с нулевой ошибкой жизни, но на самом деле есть некоторая ошибка (постоянная). Выходной сигнал регулятора производной прямо пропорционален скорости изменения ошибки во времени, как показано в уравнении. Убрав знак пропорциональности, мы получим производную константу усиления (k _d ). Как правило, производный контроллер используется, когда переменные процессора начинают колебаться или изменяются с очень высокой скоростью.D-контроллер также используется для прогнозирования будущего поведения ошибки по кривой ошибки. Математическое уравнение показано ниже;

y (t) ∝ de (t) / dt
y (t) = K  d  * de (t) / dt 

Где K _d — коэффициент пропорционального усиления.

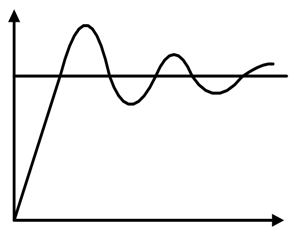
Пропорционально-интегральный регулятор:

Это комбинация контроллера P и I. Выход контроллера представляет собой сумму обоих (пропорциональных и интегральных) откликов.Математическое уравнение показано ниже;

y (t) ∝ (e (t) + ∫ e (t) dt)
y (t) = k  p  * e (t) + k  i  ∫ e (t) dt 

Пропорциональный и производный регулятор: Это комбинация P- и D-регулятора. Выход контроллера представляет собой сумму пропорциональных и производных характеристик. Математическое уравнение контроллера PD показано ниже;

y (t) ∝ (e (t) + de (t) / dt)
y (t) = k  p  * e (t) + k  d  * de (t) / dt 

Пропорциональный, интегральный и производный контроллер: Это комбинация P, I и D.Выход контроллера — это сумма пропорциональных, интегральных и производных характеристик. Математическое уравнение контроллера PD показано ниже;

y (t) ∝ (e (t) + ∫ e (t) dt + de (t) / dt)
y (t) = k  p  * e (t) + k  i  ∫ e (t) dt + k  d  * de (t) / dt 

Таким образом, комбинируя этот пропорциональный, интегральный и производный отклик управления, формирует ПИД-регулятор .

Методы настройки ПИД-регулятора:

Для получения желаемого выхода этот контроллер должен быть правильно настроен.Процесс получения идеального ответа от ПИД-регулятора с помощью настройки ПИД-регулятора называется настройкой контроллера . Средство настройки ПИД-регулятора устанавливает оптимальное значение усиления пропорционального (k _p ), производного (k _d ) и интегрального (k _i ) отклика. ПИД-регулятор настроен на подавление помех. означает пребывание в заданном заданном значении и отслеживание команд, означает, что при изменении заданного значения выходной сигнал контроллера будет следовать за новым заданным значением. Если контроллер настроен правильно, выходной сигнал контроллера будет соответствовать изменяемой уставке с меньшими колебаниями и меньшим демпфированием.

Существует нескольких методов настройки ПИД-регулятора и получения желаемого отклика. Способы настройки контроллера приведены ниже;

1. Метод проб и ошибок
2. Метод кривой реакции процесса
3. Метод Циглера-Николса
4. Релейный метод
5. Использование программного обеспечения

1. Метод проб и ошибок:

Метод проб и ошибок также известен как метод ручной настройки, и это самый простой метод.В этом методе сначала увеличивайте значение kp до тех пор, пока система не достигнет колебательного отклика, но система не должна работать нестабильно и сохранять значения kd и ki равными нулю. После этого установите значение ki таким образом, чтобы колебания системы прекратились. После этого установите значение kd для быстрого отклика.

2. Метод кривой реакции процесса:

Этот метод также известен как метод настройки Коэна-Куна. В этом методе сначала создайте кривую реакции процесса в ответ на возмущение.По этой кривой мы можем вычислить значение усиления контроллера, время интегрирования и время производной. Эта кривая определяется при ручном пошаговом тестировании процесса без обратной связи. Параметр модели можно найти по начальному шагу возмущения в процентах. По этой кривой мы должны найти наклон, мертвое время и время нарастания кривой, которые являются не чем иным, как значением kp, ki и kd.

3. Метод Цейглера-Николса:

В этом методе также сначала установите значение ki и kd в ноль.Пропорциональное усиление (kp) увеличивается до тех пор, пока не достигнет максимального усиления (ku). предельное усиление — это не что иное, как усиление, при котором выходной сигнал контура начинает колебаться. Это ku и период колебаний Tu используются для получения коэффициента усиления ПИД-регулятора из приведенной ниже таблицы.

Тип контроллера	кп	к i	кд
-P	0.5 к u
PI	0,45 к u	0,54 к u / T u
PID	0,60 к u	1,2 к u / T u	3 к u T u /40

4.Метод реле:

Этот метод также известен как метод Астрома-Хагглунда. Здесь выход переключается между двумя значениями регулирующей переменной, но эти значения выбираются таким образом, что процесс должен пересекать заданное значение. Когда переменная процесса меньше уставки, управляющий выход устанавливается на большее значение. Когда значение процесса больше заданного значения, управляющий выход устанавливается на более низкое значение и формируется выходной сигнал. Период и амплитуда этой колебательной формы волны измеряются и используются для определения конечного коэффициента усиления ku и периода Tu, которые используются в вышеуказанном методе.

5. Использование программного обеспечения:

Для настройки ПИД-регулятора и оптимизации контура доступны пакеты программного обеспечения. Эти программные пакеты собирают данные и создают математическую модель системы. По этой модели программное обеспечение находит оптимальный параметр настройки на основе эталонных изменений.

Структура ПИД-регулятора:

ПИД-регуляторы

разработаны на основе микропроцессорной технологии. Разные производители используют разную структуру и уравнение ПИД.Наиболее часто используемые уравнения PID: уравнение параллельного, идеального и последовательного ПИД-регулирования .

В уравнении параллельного ПИД-регулятора пропорциональное, интегральное и производное воздействия работают отдельно друг от друга и объединяют эффекты этих трех воздействий в системе. Блок-схема этого типа PID показана ниже;

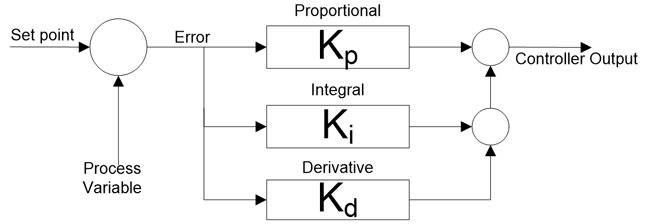
В уравнении идеального ПИД-регулятора константа усиления k _p распределяется по всему члену. Таким образом, изменение k _p влияет на все остальные члены уравнения.

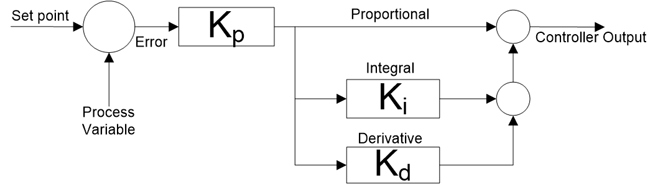
В уравнении ПИД-регулятора серии константа усиления k _p распределяется по всем элементам так же, как и уравнение идеального ПИД-регулятора, но в этом уравнении интеграл и константа производной влияют на пропорциональное действие.

Приложения ПИД-регулятора:

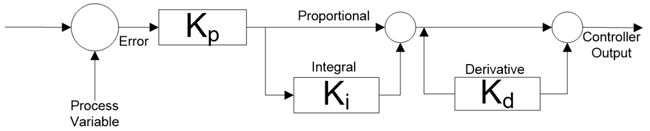
Контроль температуры:

Возьмем для примера кондиционер (кондиционер) любого завода / процесса. Уставка — это температура (20 ͦ C), а текущая температура, измеренная датчиком, составляет 28 ͦ C.Наша цель — запустить кондиционер при желаемой температуре (20 ͦ C). Теперь контроллер переменного тока генерирует сигнал в соответствии с ошибкой (8 ° C), и этот сигнал подается на переменный ток. В соответствии с этим сигналом, выходной сигнал переменного тока изменяется и температура снижается до 25 C. Далее такой же процесс будет повторяться до тех пор, пока датчик температуры не покажет желаемую температуру. Когда ошибка равна нулю, контроллер подаст команду остановки на переменный ток, и снова температура повысится до определенного значения, и снова возникнет ошибка, и тот же процесс будет повторяться непрерывно.

Проектирование контроллера заряда MPPT (отслеживание максимальной мощности) для солнечных фотоэлектрических систем:

ВАХ фотоэлемента зависит от температуры и уровня освещенности. Таким образом, рабочее напряжение и ток будут непрерывно изменяться в зависимости от изменения атмосферных условий. Поэтому очень важно отслеживать точку максимальной мощности для эффективной фотоэлектрической системы. Чтобы найти MPPT, используется ПИД-регулятор, и для этого заданное значение тока и напряжения передается контроллеру.Если атмосферные условия изменятся, этот трекер поддерживает постоянное напряжение и ток.

Преобразователь силовой электроники:

ПИД-регулятор наиболее полезен в приложениях силовой электроники, таких как преобразователи. Если преобразователь подключен к системе, в соответствии с изменением нагрузки выход преобразователя должен измениться. Например, инвертор подключен к нагрузке, при увеличении нагрузки от инвертора будет течь больше тока. Таким образом, параметры напряжения и тока не являются фиксированными, они будут меняться в соответствии с требованиями.В этом состоянии ПИД-регулятор используется для генерации импульсов ШИМ для переключения IGBT инвертора. При изменении нагрузки на контроллер подается сигнал обратной связи, который генерирует ошибку. Импульсы ШИМ генерируются в соответствии с сигналом ошибки. Таким образом, в этом состоянии мы можем получить переменный вход и переменный выход с одним и тем же инвертором.

.ПИД-регулятор

, использующий технологию FPGA

1. Введение

Начиная с 60-х годов, закон Мура предсказывает, что сложность встроенных транзисторов схемы удваивается каждые два года и остается подтвержденной. Программируемые схемы FPGA (Field Programmable Gate Array) не избежали этого закона. Начиная с первой ПЛИС, разработанной как естественное развитие CPLD (сложных программируемых логических устройств), эти схемы не переставали выигрывать в сложности и впредь интегрировались до одного миллиарда транзисторов для самых последних поколений.Такое повышение уровня интеграции привело к аналогичному росту вычислительной мощности этих схем. ПЛИС затем использовались для создания быстрых образцов ASIC (интегральных схем для конкретных приложений) и за несколько лет нашли свое место во многих областях приложений. Однако порядок производственных процессов требует все больше и больше элементов мощных вычислений. Этот тип порядка находится в постоянном развитии с развитием числовых схем вычислений.Таким образом, ПИД-регуляторы представляют собой большинство контроллеров, используемых в управлении промышленными системами. В связи с этим необходимо оцифровать алгоритм ПИД-регулирования. Современные цифровые системы управления требуют все более сильных и быстрых вычислительных компонентов. Этот тип элементов становится все же незаменим благодаря использованию некоторых новых алгоритмов управления, таких как нечеткое управление, адаптивное управление, управление скользящим режимом… [1]. Хотя ПИД-регуляторы самые старые, они представляют собой наиболее часто используемые контроллеры в промышленном управлении. системы

2.Дискретное уравнение ПИД-регулятора

Алгоритм ПИД-регулятора состоит из трех основных режимов: пропорционального режима, интегрального и производного режимов. При использовании этого алгоритма необходимо решить, какие режимы будут использоваться (P, I или D), а затем указать параметры (или настройки) для каждого используемого режима. Обычно используются три основных алгоритма P, PI или PID.

Реализация ПИД-контроллеров с использованием микропроцессоров и микросхем DSP устарела и хорошо известна [2] [3], тогда как в литературе можно найти очень мало работ о том, как реализовать ПИД-контроллеры с использованием ПЛИС [4].

Программируемые пользователем вентильные матрицы (FPGA) стали альтернативным решением для реализации цифровых систем управления, в которых ранее преобладали микропроцессорные системы общего назначения.

В нашей работе мы представляем простой метод реализации ПИД-регуляторов. Некоторые другие статьи были посвящены предложению алгоритмов настройки коэффициентов ПИД-регуляторов с использованием ПЛИС, в то время как сам контроллер все еще реализован в программном обеспечении.

В [5] авторы описывают архитектуру системы сбора данных для гамма-камеры.

За последние два года семейства Spartan II и III FPGA от Xilinx успешно использовались в различных приложениях, включая инверторы [6] [7], средства связи [8] [9], встроенные процессоры [10] и обработка изображений [11].

В нашей работе сбор данных для ПИД-регулятора, который реализован с помощью платы Xilinx Spartan-3 Starter Kit Board, основан на 8-битных последовательных аналого-цифровых преобразователях, расширяемых с платы Digilent AO1. Подобные преобразователи используются в [12] для реализации адаптируемого тензодатчика с использованием ПЛИС.

Применение ПИД-регулятора в системе управления с обратной связью показано на рис.1, где ref — сигнал уставки, y — сигнал обратной связи, e — сигнал ошибки, а u — сигнал вход управления.

Рисунок 1.

Система управления с обратной связью на основе ПИД-регулятора.

Простейшая форма алгоритма ПИД-регулирования определяется выражением:

u (t) = kp (e (t) + 1Ti∫e (t) dt + Tdde (t) dt) E1

Согласно исследованию, проведенному в [ 13] преобразованное в цифровую форму уравнение ПИД возвращается к:

uk = uk − 1 + b0⋅ek + b1⋅e (k − 1) + b2⋅e (k − 2) E2

Где коэффициенты b ₀ , b ₁ и b ₂ вычисляются по выражениям:

b0 = kp⋅ (1 + TdT); b1 = kp⋅ (−1 + TTi − 2⋅TdT); b2 = kp⋅TdTE3

Kp, Ti и Td — параметры ПИД-регулятора для настройки, а T — период выборки в секундах.

3. Архитектура цифрового ПИД-регулятора

Чтобы повысить скорость и минимизировать затраты, предлагая явно хорошие характеристики, используемая архитектура включает в себя по существу три комбинационных логических умножителя, один субстрат, три сумматора и три регистра. На рис. 2 представлена ​​принятая архитектура.

Действительно, эта архитектура требует наличия всех операторов вычислений на каждом этапе.

Рисунок 2.

Архитектура PID.

3.1.Представление блоков преобразования

Плата AIO1 — это периферийная плата, разработанная для работы с системными платами семейства Digilent. AIO1 содержит аналого-цифровые и цифро-аналоговые преобразователи от Analog Devices, два сдвоенных операционных усилителя, различные разъемы ввода / вывода аналоговых сигналов и макетную плату без пайки. Все аналоговые компоненты используют встроенный источник напряжения 5 В постоянного тока. Все неиспользуемые сигналы ввода-вывода проходят через плату AIO1, поэтому ее можно использовать между системной платой и другими периферийными платами.

AIO1 использует 8-битный аналого-цифровой преобразователь 200 Кс (AD7823) и 8-битный цифро-аналоговый преобразователь 1 МГц (AD7303), оба производства компании Analog Devices. Операционные усилители AD8534 (также от Analog Devices) могут управлять выходами 250 мА по схеме «rail-to-rail» с полосой пропускания 3 МГц, поэтому многие полезные устройства могут управляться напрямую.

Рис. 3 описывает все компоненты этого блока.

3.2. Интерфейс аналогового ввода ПЛИС

хорошо подходят для последовательных аналого-цифровых (A / D) преобразователей.Это главным образом связано с тем, что последовательный интерфейс потребляет меньше линий связи, в то время как FPGA достаточно быстра для обработки высокоскоростных последовательных данных. AD7823 — это высокоскоростной 8-разрядный аналого-цифровой преобразователь с низким энергопотреблением. Деталь содержит типичный аналого-цифровой преобразователь последовательного приближения длительностью 4 мкс и высокоскоростной последовательный интерфейс, который легко подключается к ПЛИС. Адаптер аналого-цифрового интерфейса (ADIA) реализован внутри FPGA (рисунок 5). Внутри ПЛИС этот адаптер упрощает параллельный сбор данных. Выборка инициируется на переднем фронте тактового сигнала, приложенного к выборке линии.Временная диаграмма протокола связи показана на рисунке 4. Полный период преобразования и сбора данных составляет 5,4 мкс, что позволяет производить выборку со скоростью до 185 килограммов отсчетов в секунду. Этой скорости более чем достаточно для большинства приложений ПИД-регулирования.

Рисунок 3.

Схема DIGILENT AIO1.

Рисунок 4.

Преобразователь интерфейса A / D.

Рисунок 5. Временная диаграмма

AD7823.

Выходное кодирование AD7823 является прямым двоичным.Разработанные переходы кода происходят при последовательных целочисленных значениях LSB (т. Е. 1 LSB, 2 LSB и т. Д.). Размер LSB = VREF / 256.

3.3. Интерфейс аналогового вывода

AD7303 представляет собой сдвоенный 8-разрядный цифро-аналоговый преобразователь напряжения. В этом устройстве используется универсальный трехпроводной последовательный интерфейс, работающий на частоте до 30 МГц. Регистр последовательного ввода имеет ширину 16 бит; 8 бит действуют как биты данных для цифроаналогового преобразователя, а оставшиеся 8 бит составляют регистр управления. Он связан с FPGA, как показано на рисунке 6.Адаптер интерфейса D / A (DAIA), который реализован в FPGA, обеспечивает параллельный ввод данных для двойных D / A преобразователей. Временная диаграмма протокола связи показана на рисунке 7. Период передачи выборки составляет 680 нс, что позволяет осуществлять цифро-аналоговое преобразование с превосходной скоростью 1,47 МГц.

Рисунок 6.

Преобразователь интерфейса A / D.

Рис. 7. Временная диаграмма

AD7303.

Любое выходное напряжение ЦАП в идеале можно выразить как:

VOUT = 2 × VREF × (N / 256), где: N — десятичный эквивалент двоичного входного кода.Диапазон N от 0 до 255xVREF — это напряжение, приложенное к выводу внешнего REF, когда выбрано внешнее задание, и VDD / 2, если используется внутреннее задание.

3.4. Результаты внедрения

Предлагаемый ПИД-регулятор на основе технологии Xilinx Inc FPGA может быть использован как универсальный контроллер для различных приложений. Результаты моделирования, полученные с помощью сгенерированного VHDL, в данной работе использовался симулятор ModelSim®. Схемы для ПИД-контроллеров были получены путем логического синтеза, размещения и маршрутизации с использованием Xilinx ISE 7.1i, из представления VHDL, созданного статическим анализатором. Мы используем ПЛИС Xilinx Spartan-3 xc3s200-ft256-4. Представленные здесь результаты являются оценками, полученными непосредственно из Xilinx ISE 7.1i.

Рисунок 8.

Расчетные свойства.

В таблице 1 показано минимальное количество операций умножения, сложения и регистров, необходимых для ПИД-регулятора без блока преобразования.

Арифметический номер для ПИД-регулятора.

Блок ПИД-регулятора в виде полной системы управления, состоящей из аналогового и цифрового ввода / вывода, показан на рисунке 9.

Рисунок 9.

Блок ПИД-регулятора.

Результаты моделирования, адаптированные для этого блока, показаны на рисунке 10.

Рисунок 10.

Схема моделирования блока ПИД-регулятора.

Синтез блока ПИД-регулятора с использованием ПЛИС Xilinx Spartan-3 xc3s200-ft256 -4 дает следующие результаты.

Рисунок 11.

Сводная информация об использовании устройств для реализации ПИД-регулятора.

Конструкция, эффективная с точки зрения энергопотребления и площади кристалла, означает, что микросхему FPGA можно использовать для размещения большего количества контроллеров с соответствующей скоростью и низким энергопотреблением, что приводит к снижению стоимости аппаратного обеспечения контроллера.

4. Применение ПИД-регулятора с использованием технологии FPGA для управления системой второго порядка

4.1. Представление системы

Рисунок 12 описывает систему второго порядка.

Рисунок 12.

Схема установки системы второго порядка.

Значения всех компонентов:

R = 12 k

R ₁ = 15 kΏ

R ₂ = 10 kΏ

C ₁ = 6,8 нФ

C ₂ = 22 нФ

Передаточная функция системы определяется следующим уравнением:

G (p) = Vs (p) Ve ( p) = Ks1 + 2mω0p + (1ω0) 2p2E4

С:

Ks = R2R1 = 0,67: статическое усиление

ω0 = 1RC1C2 = 6,81 * 103rd / s E5

m = C2C1 = 1,80> 1: Амортизация коэффициент

При перестановке позиций C1 и C2 коэффициент амортизации становится:

4.2. Результат эксперимента

На момент заказа системы появляются два случая; при амортизации m> 1 и m <1.

4.2.1. Результаты экспериментов для амортизации m> 1

4.2.1.1. Ответ системы приводит к открытой пряжке

Для заказа (ref) порядка 2V, примененного к системе в BO, вы получите ответ y (t), представленный на следующем рисунке.

Рисунок 13.

Ответ системы в открытой пряжке> 1.

В соответствии с этим ответом проверяется, что выходное напряжение стабилизируется без колебаний (m> 1) почти до значения 1,4 В, что более или менее соответствует теоретическому значению:

4.2.1.2. Результаты ответа системы с регулятором P

Для заказа (ref) порядка 2 В, примененного к системе, заказанной пропорциональным регулятором (P) с KP = 2, ответ y (t) представлен на следующем рисунке

Рисунок 14.

Ответ системы, заказанный пропорциональным регулятором P.

Можно заметить, что этот ответ представляет статическую ошибку порядка 40%. Теоретически эту ошибку выдает:

4.2.1.3. Результаты ответа системы с ПИ-регулятором

Для заказа (см.), Примененного порядка 2 В к системе, заказанной ПИ-регулятором с KP = 2, KI = 0.5, получаем ответ y (t), представленный на следующем рисунке:

Рисунок 15.

Ответ системы, заказанный ПИ-регулятором (m> 1). Отмена статической ошибки хорошо заметна благодаря введению I действия.

4.2.2. Результаты экспериментов для амортизации m <1

4.2.2.1. Ответ системы приводит к открытой пряжке

Для заказа (ref) порядка 2V, примененного к системе в BO, вы получите ответ y (t), представленный на следующем рисунке

Рисунок 16.

Ответ системы при открытой пряжке (m <1).

В соответствии с этим ответом проверяется, что напряжение на выходе стабилизируется с колебаниями (m <1) почти до значения 1,4V.

4.2.2.2. Результаты ответа системы с регулятором P

Для заказа (ref) порядка 2 В, примененного к системе, заказанной пропорциональным регулятором (P) с KP = 2, ответ y (t) представлен на следующем рисунке

Рисунок 17.

Ответ системы, заказанный пропорциональным регулятором P.

Можно заметить, что этот ответ представляет собой статическую ошибку порядка 40%. Теоретически эту ошибку выдает:

4.2.2.3. Результаты ответа системы с регулятором PD

Для заказа (ref) порядка 2 В, применяемого к системе, заказанной регулятором PD с KP = 2, KD = 1, будет получен ответ y (t), представленный на следующем рисунке

Рис. 18.

Ответ системы, заказанный пропорциональным регулятором P D.

Можно заметить, что ответ получил меньше колебаний, чем тот, который имеет регулирующее P, благодаря действию производной.

4.2.2.4. Результаты ответа системы с ПИ-регулятором

Для заказа (справки) порядка 2 В, применяемого к системе, заказанной ПИ-регулятором с KP = 2, KI = 0,5, будет получен ответ y (t), представленный на следующем Рисунок.

Рисунок 19.

Ответ системы, заказанный пропорциональным регулятором P I.

, хорошо замечается устранение статической ошибки благодаря введению действия I

4.2.2.5. Результаты ответа системы с ПИД-регулятором

Для заказа (ref) порядка 2 В, применяемого к системе, заказанной регулятором PI D с KP = 2, KD = 1 и KI = 0, 5, получается ответ y (t ) представлен на следующем рисунке

Рисунок 20.

Ответ системы, заказанной пропорциональным регулятором P ID.

Можно заметить, что с добавлением действия производной происходит небольшое уменьшение колебаний по сравнению с ответом, полученным регулирующим PI.

4.3. Предварительная оценка периода выборки

Проследив эволюцию порядка u (t), можно экспериментально оценить значение периода выборки (T), как показано на следующем рисунке

Рисунок 21.

Предварительная оценка периода выборки (T).

Согласно рисунку 21, оценивается значение периода выборки (T), которое составляет порядка 6,7 мкс.

5. Заключение

Цифровой ПИД-контроллер, реализованный в технологии FPGA, является настраиваемым контроллером с точки зрения задержки, разрешения и параллелизма.

Скорость, выполнение или задержку контроллера можно точно контролировать с помощью количества повторного использования арифметических элементов, например, скорость выполнения ПИД-контроллера на базе FPGA может быть менее 100 нс, если это необходимо для требований высокой пропускной способности.

Реализация ПИД-контроллеров на ПЛИС обеспечивает скорость, точность, мощность, компактность и снижение стоимости по сравнению с другими методами цифровой реализации.

В будущем форке мы планируем исследовать реализацию контроллеров нечеткой логики на ПЛИС. Также мы планируем изучить встроенные программные процессоры, такие как MicroBlaze, и изучить некоторые приложения, в которых разделение проекта между программным и аппаратным обеспечением обеспечивает лучшую реализацию.

.

ПИД-регулятор с непрерывным или дискретным временем

Время дискретного интегратора, представленное как скаляр в блок. Вы можете использовать собственное значение дискретное время дискретизации интегратора, определяющее скорость, с которой будет выполняться блок либо в Simulink, либо на внешнем оборудовании.Значение времени интегратора дискретного времени должно соответствовать средняя частота дискретизации внешнего прерывания, когда блок используется внутри условно-исполняемая подсистема.

Другими словами, вы можете указать Ц для любого интегратора методы ниже, чтобы значение соответствовало средняя частота дискретизации внешних прерываний.В дискретном времени производный член передаточная функция контроллера:

где α ( z ) зависит от метода интегратора, который вы указываете с помощью этот параметр.

Вперед Эйлер

Назад Эйлер

Трапецеидальная

Для получения дополнительной информации о дискретном времени интеграции, см. Дискретное время Справочная страница блока интегратора.Для большего информация об условно исполняемых подсистемах, см. Обзор условно выполняемых подсистем.

Зависимости

Чтобы включить этот порт, установите Время. Домен на Дискретное время и выберите ПИД-регулятор внутри условно исполняемая подсистема вариант.

Типы данных: одиночный | двойной | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

.

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

2019 © Все права защищены.

Карта сайта

Умножение	3
Сложение	3
вычитание	1
Таблица регистра	3