8-900-374-94-44
В начале 90-х создание трёхмерного игрового движка означало, что вы заставите машину выполнять почти не свойственные ей задачи. Персональные компьютеры того времени предназначались для запуска текстовых процессоров и электронных таблиц, а не для 3D-вычислений с частотой 70 кадров в секунду. Серьёзным препятствием стало то, что, несмотря на свою мощь, ЦП не имел аппаратного устройства для вычислений с плавающей запятой. У программистов было только АЛУ, перемалывающее целые числа.
При написании книги Game Engine Black Book: Wolfenstein 3D я хотел наглядно показать, насколько велики были проблемы при работе без плавающей запятой. Мои попытки разобраться в числах с плавающей запятой при помощи каноничных статей мозг воспринимал в штыки. Я начал искать другой способ. Что-нибудь, далёкое от и их загадочных экспонент с мантиссами. Может быть, в виде рисунка, потому что их мой мозг воспринимает проще.
В результате я написал эту статью и решил добавить её в книгу. Не буду утверждать, что это моё изобретение, но пока мне не приходилось видеть такого объяснения чисел с плавающей запятой. Надеюсь, статья поможет тем, у кого, как и у меня, аллергия на математические обозначения.
Цитирую Дэвида Голдберта (David Goldbert):
Для многих людей арифметика с плавающей запятой кажется каким-то тайным знанием.
Полностью с ним согласен. Однако важно понимать принципы её работы, чтобы полностью осознать её полезность при программировании 3D-движка. В языке C значения с плавающей запятой — это 32-битные контейнеры, соответствующие стандарту IEEE 754. Они предназначены для хранения и выполнения операций над аппроксимациями вещественных чисел. Пока я видел только такое их объяснение. 32 бита разделены на три части:
Внутренности числа с плавающей запятой.
Три части числа с плавающей запятой.
Пока всё нормально. Пойдём дальше. Способ интерпретации чисел обычно объясняется с помощью такой формулы:
Именно это объяснение чисел с плавающей запятой все ненавидят.
И здесь я обычно начинаю терять терпение. Возможно, у меня аллергия на математическую нотацию, но когда я это читаю, в моём мозгу ничего не «щёлкает». Такое объяснение похоже на способ рисования совы:
Хоть это изложение и верно, такой способ объяснения чисел с плавающей запятой обычно не даёт нам никакого понимания. Я виню эту ужасную запись в том, что она разочаровала тысячи программистов, испугала их до такой степени, что они больше никогда не пытались понять, как же на самом деле работают вычисления с плавающей запятой. К счастью, их можно объяснить иначе. Воспринимайте экспоненту как окно (Window) или интервал между двумя соседними целыми степенями двойки.
Три части числа с плавающей запятой.
Окно сообщает нам, между какими двумя последовательными степенями двойки будет число: [0,1], [1,2], [2,4], [4,8] и так далее (вплоть до [,]. Смещение разделяет окно на сегментов. С помощью окна и смещения можно аппроксимировать число. Окно — это отличный механизм защиты от выхода за границы. Достигнув максимума в окне (например, в [2,4]), можно «переплыть» вправо и представить число в пределах следующего окна (например, [4,8]). Ценой этого будет только небольшое снижение точности, потому что окно становится в два раза больше.
Викторина: сколько точности теряется, когда окно закрывает больший интервал? Давайте возьмём пример с окном [0,1], в котором 8388608 смещений накладываются на интервал размером 1, что даёт нам точность . В окне [2048,4096] 8388608 смещений накладываются на интервал , что даёт нам точность .
На рисунке ниже показано, как кодируется число 6,1.
Окно должно начинаться с 4 и заканчиваться следующей степенью двойки, т.е. 8. Смещение находится примерно посередине окна.
Значение 6,1 аппроксимированное с помощью числа с плавающей запятой.
Давайте возьмём ещё один пример с подробным вычислением представлением в виде числа с плавающей точкой хорошо известного всем нам значения: 3,14.
В двоичном виде это преобразуется в следующее:
Двоичное представление с плавающей точкой числа 3,14.
То есть значение 3,14 аппроксимируется как 3,1400001049041748046875.
Соответствующее значение в непонятной формуле:
И, наконец, графическое представление с окном и смещением:
Окно и смещение числа 3,14.
Интересный факт: если модули операций с плавающей запятой были такими медленными, почему в языке C в результате использовали типы float и double? Ведь в машине, на которой изобретался язык (PDP-11), не было модуля операций с плавающей запятой! Дело в том, что производитель (DEC) пообещал Деннису Ритчи и Кену Томпсону, что в следующей модели он будет. Они были любителями астрономии и решили добавить в язык эти два типа.
Интересный факт: те, кому в 1991 году действительно нужен был аппаратный модуль операций с плавающей запятой, могли его купить. Единственными, кому он мог понадобиться в то время, были учёные (по крайней мере, так Intel понимала потребности рынка).
На рынке они позиционировались как «математические сопроцессоры». Их производительность была средней, а цена огромной (200 долларов 1993 года — это 350 долларов в 2016 году.). В результате уровень продаж оказался посредственным.
Надеюсь, статья была вам полезна!
| Устройство цифровых процессоров | ||
|---|---|---|
| Архитектура | Гарвардская • Фон Неймана • Битовые операции • Система команд • Кольца защиты • RISC • MISC • EPIC • | |
| Параллелизм | Упреждающее выполнение • Конвейер • Суперскалярность • Подмена регистров • Мультипроцессор • Многопоточность | |
| Компоненты | АЛУ • Математический сопроцессор • Корпус • Векторный процессор • Регистры • Кэш | |
| Питание | Динамическое изменение частоты • Динамическое изменение напряжения | |
| Реализации | Микропроцессор • Графический процессор • Физический процессор • DSP • Система на кристалле • Микроконтроллер • ПЛИС | |
Числа с плавающей запятой представлены в аппаратном обеспечении компьютера как основание 2 (двоичное)
дроби.
Например, десятичная дробь 0,125 имеет значение 1/10 + 2/100 + 5/1000, и таким же образом двоичная дробь
К сожалению, большинство десятичных дробей не могут быть точно представлены в двоичном виде. дроби. Следствием этого является то, что, как правило, десятичное число с плавающей запятой числа, которые вы вводите, только аппроксимируются двоичными числами с плавающей запятой фактически хранится в машине.
Задачу легче понять сначала в десятичной системе счисления. Рассмотрим дробь 1/3. Вы можете аппроксимировать это как дробь с основанием 10:
или лучше
или лучше
и так далее. Независимо от того, сколько цифр вы готовы записать, результат
никогда не будет ровно 1/3, но будет все более и более лучшим приближением к
1/3.
Таким же образом, независимо от того, сколько цифр с основанием 2 вы хотите использовать, десятичное значение 0,1 не может быть представлено точно как дробь с основанием 2. В базе 2, 1/10 — бесконечно повторяющаяся дробь
.0.0001100110011001100110011001100110011001100110011...
Остановитесь на любом конечном числе битов, и вы получите приближение. На большинстве
современных машинах числа с плавающей запятой аппроксимируются с помощью двоичной дроби с
числитель, использующий первые 53 бита, начиная со старшего бита и
со знаменателем как степень двойки. В случае 1/10 двоичная дробь 3602879701896397 / 2 ** 55 что близко, но не совсем
равно истинному значению 1/10.
Многие пользователи не знают об аппроксимации из-за того, как значения
отображается. Python печатает только десятичное приближение к истинному десятичному
значение двоичной аппроксимации, сохраненное машиной. На большинстве машин, если
Python должен был печатать истинное десятичное значение сохраненного двоичного приближения.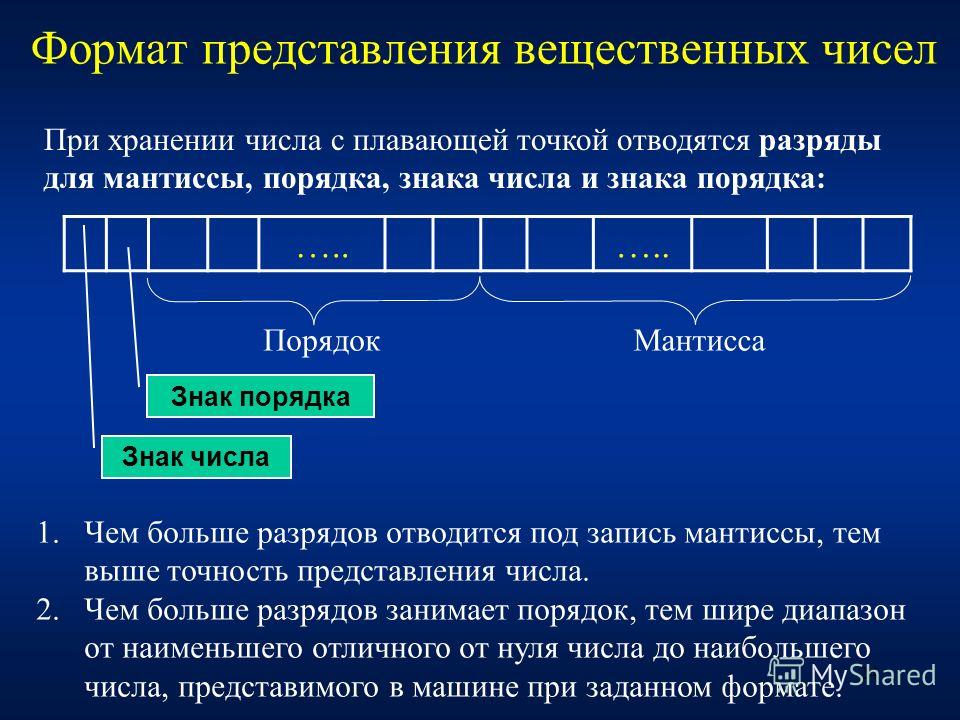
для 0.1 он должен отображать
>>> 0,1 0,1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считает нужным, поэтому Python сохраняет это число. цифр, управляемых отображением округленного значения вместо
>>> 1 / 10 0,1
Просто помните, даже если напечатанный результат выглядит как точное значение 1/10 фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что есть много разных десятичных чисел, которые имеют одинаковые
ближайшая приближенная двоичная дробь. Например, цифры 0,1 и 0,10000000000000001 и 0.1000000000000000055511151231257827021181583404541015625 все
аппроксимируется 3602879701896397/2 ** 55 . Поскольку все эти десятичные
значения имеют одинаковое приближение, любое из них может быть отображено
сохраняя при этом инвариант eval(repr(x)) == x .
Исторически, подсказка Python и встроенная функция repr() выбирали
тот, у которого 17 значащих цифр, 0. . Начиная с
Python 3.1, Python (в большинстве систем) теперь может выбирать самый короткий из
их и просто отображать 
10000000000000001 0.1 .
Обратите внимание, что это заложено в самой природе двоичных чисел с плавающей запятой: это не ошибка. в Python, и это также не ошибка в вашем коде. Вы увидите такой же вещь на всех языках, которые поддерживают арифметику с плавающей запятой вашего оборудования (хотя некоторые языки могут не отображать разницу по умолчанию или во всех режимы вывода).
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного количества значащих цифр:
>>> format(math.pi, '.12g') # дать 12 значащих цифр '3.14159265359' >>> format(math.pi, '.2f') # указать 2 цифры после точки «3.14» >>> repr(math.pi) '3.141592653589793'
Важно понимать, что это в действительности иллюзия: вы просто округляя отображаемое истинное значение машины.
Одна иллюзия может породить другую.
Например, поскольку 0,1 не совсем 1/10,
суммирование трех значений 0,1 также может не дать ровно 0,3:
>>> .1 + .1 + .1 == .3 ЛОЖЬ
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10 и
0,3 не может приблизиться к точному значению 3/10, тогда предварительное округление с функция round() не может помочь:
>>> раунд(.1, 1) + раунд(.1, 1) + раунд(.1, 1) == раунд(.3, 1) ЛОЖЬ
Хотя числа нельзя приблизить к их предполагаемым точным значениям,
функция round() может быть полезна для последующего округления, так что результаты
с неточными значениями становятся сравнимыми друг с другом:
>>> раунд(.1 + .1 + .1, 10) == раунд(.3, 10) Истинный
Двоичная арифметика с плавающей запятой таит в себе много подобных сюрпризов. Проблема
с «0,1» подробно объясняется ниже, в разделе «Ошибка представления».
раздел. См. Опасности с плавающей запятой
для более полного описания других распространенных сюрпризов.
Как сказано в конце, «простых ответов не бывает». Тем не менее, не будьте чрезмерно опасайтесь чисел с плавающей запятой! Ошибки в операциях Python с плавающей запятой наследуются от оборудования с плавающей запятой, и на большинстве машин порядка нет более 1 части в 2**53 за операцию. Этого более чем достаточно для большинства задачи, но нужно иметь в виду, что это не десятичная арифметика и что каждая операция с плавающей запятой может привести к новой ошибке округления.
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования операций с плавающей запятой
арифметики вы увидите результат, который вы ожидаете в конце, если вы просто округлите
отображение ваших окончательных результатов до ожидаемого количества десятичных цифр.
9Обычно достаточно 0005 str() , а для более точного управления см. str.format() спецификаторы формата метода в синтаксисе строки формата.
Для случаев использования, требующих точного десятичного представления, попробуйте использовать decimal Модуль , который реализует десятичную арифметику, подходящую для
бухгалтерские приложения и высокоточные приложения.
Другая форма точной арифметики поддерживается модулем дробей .
который реализует арифметику, основанную на рациональных числах (такие числа, как
1/3 можно представить точно).
Если вы интенсивно используете операции с плавающей запятой, вам следует взглянуть
в пакете NumPy и многих других пакетах для математических и
статистические операции, предоставляемые проектом SciPy. См.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно сделать хотите знать точное значение числа с плавающей запятой. метод float.as_integer_ratio() выражает значение числа с плавающей запятой как
дробь:
>>> х = 3,14159>>> x.as_integer_ratio() (3537115888337719, 1125899906842624)
Поскольку соотношение является точным, его можно использовать для воссоздания без потерь исходное значение:
>>> х == 3537115888337719 / 1125899906842624 Истинный
Метод float. выражает число с плавающей запятой в шестнадцатеричном
16), снова указав точное значение, хранящееся на вашем компьютере:
hex()
>>> x.hex() '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для восстановления значение с плавающей запятой точно:
>>> x == float.fromhex('0x1.921f9f01b866ep+1')
Истинный
Поскольку представление точное, оно полезно для надежного переноса значений между различными версиями Python (независимость от платформы) и обмен данные с другими языками, которые поддерживают тот же формат (например, Java и C99).
Другим полезным инструментом является функция math.fsum() , которая помогает смягчить
потеря точности при суммировании. Он отслеживает «потерянные цифры» по мере того, как значения
добавляется к нарастающей сумме. Это может повлиять на общую точность
чтобы ошибки не накапливались до такой степени, что они влияют на
окончательный итог:
>>> сумма([0.1] * 10) == 1.0 ЛОЖЬ >>> math.fsum([0.1] * 10) == 1.0 Истинный
В этом разделе подробно объясняется пример «0.1» и показано, как можно выполнить точный анализ подобных случаев самостоятельно. Базовое знакомство с бинарником предполагается представление с плавающей запятой.
Ошибка представления относится к тому факту, что некоторые (фактически большинство) десятичные дроби не могут быть представлены точно как двоичные дроби (с основанием 2). Это главная причина, по которой Python (или Perl, C, C++, Java, Fortran и многие другие) другие) часто не будет отображать точное десятичное число, которое вы ожидаете.
Почему? 1/10 нельзя точно представить в виде двоичной дроби. Почти все
машины сегодня (ноябрь 2000 г.) используют арифметику с плавающей запятой IEEE-754, и
почти все платформы отображают Python с плавающей запятой в соответствии с IEEE-754 «двойной точностью». 754
числа double содержат 53 бита точности, поэтому при вводе компьютер стремится
преобразовать 0,1 в ближайшую дробь, которая может иметь вид J /2** N , где J равно
целое число, содержащее ровно 53 бита.
Переписывание
1/10 ~= Дж/(2**Н)
как
Дж ~= 2**Н / 10
и вспоминая, что J имеет ровно 53 бита (равно >= 2**52 , но < 2**53 ),
лучшее значение для N 56:
>>> 2**52 <= 2**56 // 10 < 2**53 Истинный
То есть 56 — это единственное значение для N , которое оставляет J ровно с 53 битами. наилучшее возможное значение для J - это округленное частное:
>>> q, r = divmod(2**56, 10) >>> г 6
Поскольку остаток больше половины от 10, получается наилучшее приближение округляя:
>>> д+1 7205759403792794
Следовательно, наилучшее возможное приближение к 1/10 в 754 с двойной точностью:
7205759403792794/2**56
Деление числителя и знаменателя на два уменьшает дробь до:
3602879701896397/2**55
Обратите внимание, что, поскольку мы округлили, на самом деле это немного больше, чем 1/10;
если бы мы не округляли, то частное было бы немного меньше, чем
1/10.
Но ни в коем случае нельзя ровно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: он видит точную заданную дробь. выше, лучшее 754 двойное приближение, которое он может получить:
>>> 0,1 * 2 ** 55 3602879701896397.0
Если мы умножим эту дробь на 10**55, мы увидим значение, равное 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 1000000000000000055511151231257827021181583404541015625
означает, что точное число, хранящееся в компьютере, равно десятичное значение 0,1000000000000000055511151231257827021181583404541015625. Вместо отображения полного десятичного значения многие языки (включая более старые версии Python), округляем результат до 17 значащих цифр:
>>> формат (0.1, '.17f') «0,10000000000000001»
дроби и десятичные модули делают эти расчеты
легко:
>>> из десятичного импорта Decimal >>> из дробей импорт дроби >>> Дробь.from_float(0.
В компьютере действительные числа представляются с конечной точностью. Хотя в большинстве случаев можно с уверенностью предположить, что результат арифметической операции, выполненной на вашем компьютере, является правильным, важно помнить, что такое представление с конечной точностью приводит к неизбежным ошибкам, особенно когда числа с плавающей запятой являются цифровыми приближениями. к действительным числам, участвуют.
Примечание: Прежде чем использовать числа с плавающей запятой, мы рекомендуем получить четкое представление о ваших данных, чтобы вы могли понять, какой уровень точности вам нужен.
Остальная часть этого раздела дает некоторые сведения о последствиях использования чисел с плавающей запятой в ваших арифметических операциях.
Примечание: Точность чисел одинарной и двойной точности в IDL зависит как от платформы, так и от компилятора. Поскольку IDL написан на C, числа в IDL будут вести себя идентично программе, написанной на C на вашей платформе. Подробную информацию о компиляторе и флагах компиляции для вашей платформы можно найти в системной переменной !MAKE_DLL.
Чтобы понять, почему числа с плавающей запятой по своей природе неточны, рассмотрим следующее:
Другими словами, значения с плавающей запятой представляют собой аппроксимации с конечной точностью бесконечно точных чисел.
Например, некоторые числа могут быть точно представлены числами одинарной точности с плавающей запятой:
PRINT, 2.0, FORMAT='(f25.16)'
ПЕЧАТЬ, 2.0 EQ 2.0d ? 'true': 'false'
Дисплей IDL:
2.000000000000000000
True
Другие числа не совсем репрезентативны:
Печать, 0,1, формат = '(f25.16)'
, 0,1, 0,1. 0,1д? 'true' : 'false'
Отображает IDL:
0.10000000141
false
Из-за того, что они вызывают числа с плавающей запятой с двойной точностью, при использовании многих математических функций IDL может дать немного другие результаты.
Для получения дополнительной информации о числах с плавающей запятой обратитесь к стандарту IEEE для арифметики с плавающей запятой (IEEE 754), обобщенному на Wikipedia.
org.
При работе с арифметикой с плавающей запятой полезно учитывать величину, известную как машинная точность или точность с плавающей запятой вашего конкретного компьютера. Это наименьшее число, которое при добавлении к 1,0 дает результат с плавающей запятой, отличный от 1,0.
Полезно думать о машинной точности, рассматривая ее как дробную точность, с которой представляются числа с плавающей запятой. Другими словами, машинная точность примерно соответствует изменению младшего бита мантиссы с плавающей запятой — именно то, что может произойти, если число с большим числом значащих цифр, чем помещается в мантисса с плавающей запятой, будет округлено, чтобы соответствовать доступному пространству. . Вообще говоря, каждая арифметическая операция с плавающей запятой вносит в результат ошибку, по крайней мере равную машинной точности. Эта ошибка известна как ошибка округления.
Ошибки округления накапливаются. В зависимости от используемого алгоритма вычисление, включающее n арифметических операций, может иметь общую ошибку округления между SQRT( n ), умноженной на машинную точность, и n , умноженной на машинную точность.
Обратите внимание, что машинная точность не равна наименьшему числу с плавающей запятой, которое может представить ваш компьютер. Чтобы найти эти и другие машинно-зависимые величины для своего компьютера, см. MACHAR.
В некоторых численных алгоритмах также присутствует другой тип ошибки. Ошибка усечения — это ошибка, возникающая в процессе численного приближения непрерывной функции путем ее оценки в конечном числе дискретных точек. Часто точность можно повысить (опять же за счет некоторого времени вычислений) за счет увеличения числа оцениваемых дискретных точек.
Например, рассмотрим процесс вычисления
Очевидно, что ответ становится более точным, когда n приближается к бесконечности. Однако при выполнении фактического вычисления значение отсечки должно быть указано для n . Увеличение n уменьшает ошибку усечения за счет вычислительных усилий.
В некоторых подпрограммах IDL в таких случаях можно указать пороговые значения (см.
, например, INT_2D). При написании собственных подпрограмм на IDL важно учитывать компромисс между точностью и временем вычислений.
Ниже приведено краткое описание подпрограмм IDL для проверки состояния математических ошибок и характеристик машины.
Обычный | Описание |
CHECK_MATH | Возвращает и очищает состояние накопленной математической ошибки. |
КОНЕЧНО | Возвращает True, если его аргумент конечен. |
1] * 10) == 1.0
ЛОЖЬ
>>> math.fsum([0.1] * 10) == 1.0
Истинный
1)
Дробь(3602879701896397, 36028797018963968)
>>> (0.1).as_integer_ratio()
(3602879701896397, 36028797018963968)
>>> Десятичный.from_float(0.1)
Десятичный('0.1000000000000000055511151231257827021181583404541015625')
>>> формат(десятичный.from_float(0.1), '.17')
«0,10000000000000001»
