8-900-374-94-44
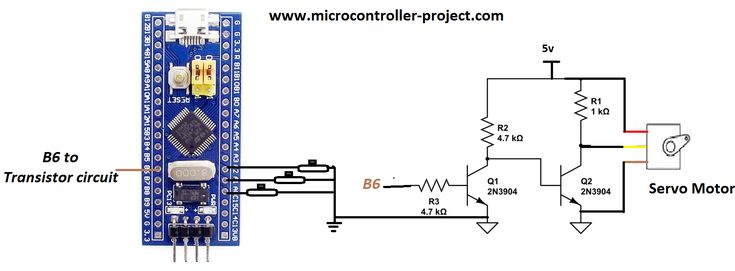
Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.
Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.
С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.
К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:
Частота является величиной, обратной периоду времени, (). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.
Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.
Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1 секунда для совершения полного цикла, имеет период равный одной секунде.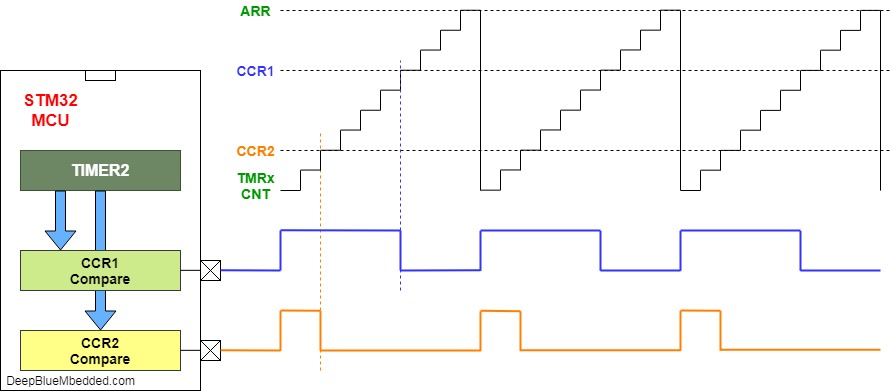
Аналогично, для синусоидального сигнала, которому требуется 5 секунд для совершения полного цикла, имеет период равный 5 секундам, и так далее.
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.
Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то (T = ).
Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.
Соотношения между периодом сигнала и его частотой:
Гц
c
Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц
| Префикс | Определение | Запись | Период |
| Кило | тысяча | кГц | 1 мс |
| Мега | миллион | МГц | 1 мкс |
| Гига | миллиард | ГГц | 1 нс |
| Тера | триллион | ТГц | 1 пс |
Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов.
Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.
Для меандра, время заполнения равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
Гц
Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.
Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом.
В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.
Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.
На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.
Отношение периода повторения сигнала , к длительности положительного импульса , называют скважностью:
Величину обратную скважности называют коэффициентом заполнения (duty cycle):
Пример расчета
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%.
Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
Гц
Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».
Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями.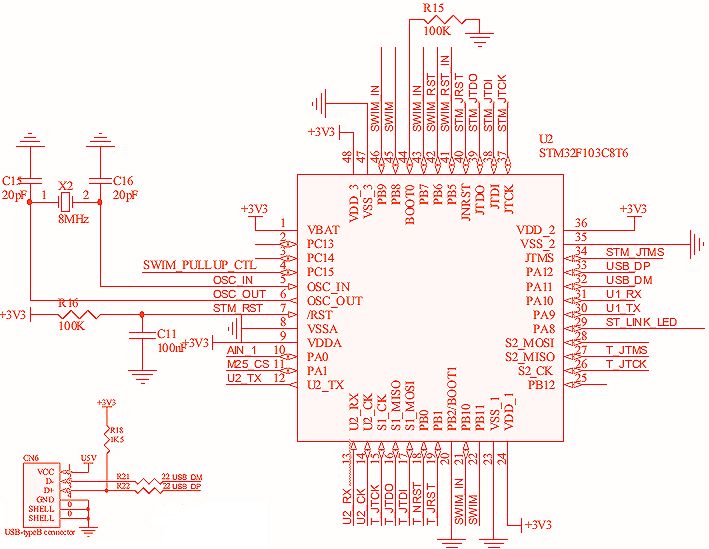
Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.
В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.
Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.
Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал. Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения.
Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.
Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
Я рассмотрел здесь только основные виды электрических сигналов. Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например:
Подробно я вернусь к ним в своих последующих публикациях.
Вы можете пропустить чтение записи и оставить комментарий.
Размещение ссылок запрещено.
Сегодня подробно рассмотрим доступный универсальный измеритель от FNIRSI. Модель DSO-TC2 включает в себя цифровой одноканальный осциллограф (до 200 кГц), тестер электронных компонентов и генератор сигналов PWM. Имеется экран 2.4″ (320х240), и устройство работает от встроенного аккумулятора 1500 мАч. Интересный вариант комплексного измерителя для начинающих радиолюбителей.
Традиционно начнем обзор с заявленных характеристик продукта.
Технические характеристики
Модель: DSO-TC2
Экран: 2.4″ TFT с подсветкой
Частота дискретизации: 2.5 Мс/с
Полоса пропускания Anolog: 0-200 кГц
Входное сопротивление: 1MΩ
1:1 щупы: 80Vpp (± 40V)
10:1 щупы: 800Vpp (± 400V)
Вертикальная чувствительность: 10 мВ/див ~ 10 В/див (с шагом 1-2-5)
Горизонтальные диапазоны времени: 10US/Div ~ 500s/Div (с шагом 1-2-5)
01Ω ~ 50MΩ
(для измерения компонентов)Опциональные щупы с делителем (марка 6100) с переходником для подключения к DSO-TC2:
Внешний вид и особенности конструкции
Переходим к внешнему осмотру измерителя.
Выполнен он в пластиковом корпусе черного и желтого цвета. Шесть механических кнопок прорезинены и нажимаются тактильно четко. Под экраном размещен слот для выводов тестируемым деталей, зажим рычажком.
На нижнем: порт usb С для зарядки и подключения к ПК для смены прошивки (устройство видно на ПК как внешний носитель).
В интернете есть фото платыDSO-TC2:
Используется микроконтроллер MM32F103RET6 для тестера компонентов и Ch42F103C8T6 для осциллографа (клоны STM32), кварцы 8 МГц.
Эксплуатация
Перед началом использования заряжаем измеритель от любого зарядного 5 В:
Эту разницу напряжения, между зарядом и разрядом измеряет тестер.Потеря напряжения дает оценку добротности(качества) конденсатора, измеряется в процентах. Но не показывает ESR, что важнее. Но может быть допилят в будущем обновлении ПО.Минусы:
Спасибо за внимание.
Удачных покупок!
Товар для написания обзора предоставлен магазином. Обзор опубликован в соответствии с п.18 Правил сайта.
\$\начало группы\$
Я работаю над проектом, который требует фазовой синхронизации (в цифровом виде) выходного сигнала датчика с эталонным сигналом, который необходимо выполнить на микроконтроллере STM32. Я новичок в этой области и только что прочитал базовую теорию контура фазовой автоподстройки частоты и прямого цифрового синтезатора, однако я потерялся, чтобы даже начать.
Я хочу разбить свою задачу на генерацию синусоид для DDS, а затем разработать PLL в микроконтроллере.
Для начала я подумал о создании синусоидальной волны на основе таблицы поиска, которую я могу либо импортировать из другой программы, либо создать функцию для генерации непосредственно в stm32cubeIDE.
Однако это не работает, потому что у нас есть сигнал фиксированной частоты. Для PLL мы должны иметь возможность изменять выходную частоту, и мы могли бы сделать это либо путем изменения размера таблицы поиска, значения предварительного делителя или ARR. Но как это сделать для PLL, не изменяя значения вручную?
Если у кого-то есть идеи по этой теме, не могли бы вы помочь мне начать работу и дать мне больше информации по этой теме?
\$\конечная группа\$
4
\$\начало группы\$
По сути, вам нужно сгенерировать LUT для вашей фиксированной частоты. Вам нужно сделать это только один раз, затем используйте фазовый аккумулятор для генерации любой частоты, которая вам нужна. Возможно, вам придется настроить для получения более высокой точности, используя линейную интерполяцию между значениями LUT.
Здесь был аналогичный вопрос, который может быть интересен для вашего приложения и может подойти для вашего требования. Удачи !
\$\конечная группа\$
0
\$\начало группы\$
Если вам нужно сгенерировать синусоиду с переменной частотой, но с фиксированной частотой дискретизации, вы можете подумать о написании кода в MCU, который будет действовать как «резонатор».
Этот код по сути является цифровым фильтром, но с коэффициентами, выбранными таким образом, чтобы его выходной сигнал не затухал и не стабилизировался, а фактически поддерживал себя во многом так же, как аппаратно работает генератор с фазовым сдвигом.
Я использовал эту технику много лет назад и позаимствовал идею из старой (возможно, уже древней) заметки о приложении от Microchip.
Это примечание к приложению ориентировано на создание тональных сигналов набора номера DTMF путем независимого создания двух синусоидальных сигналов, а затем их сложения вместе для создания окончательного «двухтонального сигнала».
Такой способ означает, что вам не нужна справочная таблица для хранения синусоидальной волны с достаточным разрешением, а вместо этого означает, что ваш MCU должен быть достаточно быстрым, чтобы выполнять необходимые вычисления для каждого временного интервала.
Учитывая, что вы предлагаете использовать STM32, предположительно работающий на частоте 100 МГц или около того, я не думаю, что это будет проблемой.
В коде, который я написал, мне удалось заставить 8-битный PIC, работающий на частоте 16 МГц, генерировать 2 синусоидальных сигнала в диапазоне 200-300 Гц, дискретизированных на частоте около 10 кГц, с достаточной вычислительной мощностью для одновременной передачи данных по UART на частоте 115200, а также некоторые другие обязанности обработки.
В первоначальной версии основная часть кода была написана на C, но у меня был оптимизированный вручную ассемблер для наиболее важных частей.
В более поздних версиях, когда я смог использовать более быстрый MCU, я перенес весь код на новое устройство и написал его на C.
\$\конечная группа\$
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Электронная почта
Требуется, но никогда не отображается
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Главная Прикладная механика и материалы Прикладная механика и материалы Vols.
608-609 Разработка синусоидального инверторного источника питания на основе…
Предварительный просмотр статьи
В документе проектируется высокопроизводительный сетевой инвертор мощностью 20 кВт на базе процессора STM, описывается общая структура инвертора, а также разрабатывается аппаратная схема и схема проектирования программного обеспечения; наконец произвести прототип и испытать. Результаты экспериментов показывают, что: в условиях номинальной мощности инвертор может стабилизировать выходное допустимое значение 220 В 3%, частота синусоидального переменного тока 50 Гц, выходное напряжение имеет низкое содержание гармоник и высокую надежность, и имеет хорошие перспективы применения в области фотоэлектрическая энергетика.
Доступ через ваше учреждение
Вас также могут заинтересовать эти электронные книги
Предварительный просмотр
* — Автор, ответственный за переписку
Рекомендации
[1]
Т.
Керекес, Р. Теодореску, П. Родригес Г., Васкес и Э. Альдабас. Новая высокоэффективная топология однофазного бестрансформаторного фотоэлектрического инвертора. IEEE Transactions on Industrial Electronics, 2001, 58, 1184-191.
DOI: 10.1109/tie.2009.2024092
Академия Google
[2] Дж. Селварадж Н.А. Рахим, К. Крисмадината. Цифровой PI-регулятор тока для фотоэлектрического инвертора, подключенного к сети. Промышленная электроника и приложения, 2008: 742-746.
DOI: 10.
1109/icea.2008.4582614
Академия Google
[3] Г. Васкес, Т. Керекес, А. Ролан, Д. Агилар, А. Луна и Г. Азеведо. Потери и оценка CMV в безтрансформаторных фотоэлектрических топологиях, подключенных к сети. Международный симпозиум IEEE по промышленной электронике. 2009 г.: 544-548.
DOI: 10.1109/isie.2009.5213296
Академия Google
[4]
У Кайфу, Чжан Цзяньсюань, Чен Юкай и др.
Солнечная фотоэлектрическая система производства электроэнергии и освещения. Пекин: Научная пресса (2009 г.).).
Академия Google
[5] Чжун Яньпин. Схема силовой электронной схемы. Ухань: Издательство Хуачжунского университета науки и технологий (2009 г.).
Google Scholar
[6] Гуй Айган, Хо Цзинь Ван, Лю Цзяньго. Униполярный расчет точки переключения модуляции формы сигнала SPWM и гармонический анализ. RiverMassey Energy, 2008, (2): 27-31.
Академия Google
[7]
Цзи Юпи Се Юньсян.
Необходимо найти частоту этого сигнала.