Значение ацп: АЦП — что это такое? — диспротект.рф — "ДИС-протект", системы безопасности

23.06.2023| alexxlab| Нет комментариев

Значение ацп: АЦП — что это такое?

Содержание

Аналого-цифровое преобразование для начинающих / Хабр

В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

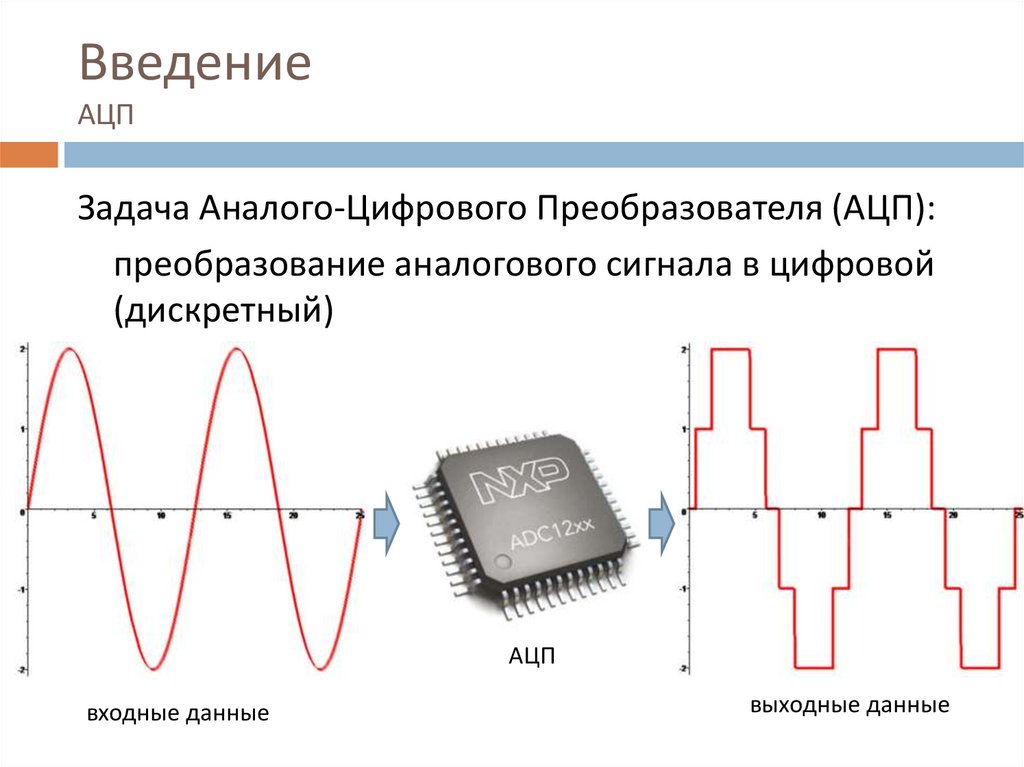
Введение

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.

п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.

Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.

Основные характеристики АЦП

АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно).

Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.

Типы АЦП

Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:

АЦП параллельного преобразования (прямого преобразования, flash ADC)
АЦП последовательного приближения (SAR ADC)
дельта-сигма АЦП (АЦП с балансировкой заряда)

Существуют также и другие типы АЦП, в том числе конвейерные и комбинированные типы, состоящие из нескольких АЦП с (в общем случае) различной архитектурой. Однако приведенные выше архитектуры АЦП являются наиболее показательными в силу того, что каждая архитектура занимает определенную нишу в общем диапазоне скорость-разрядность.

Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.

Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.

Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.

Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.

АЦП прямого преобразования

АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.

Архитектура АЦП прямого преобразования изображена на рис. 1

Рис. 1. Структурная схема АЦП прямого преобразования

Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.

Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром. N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.

АЦП последовательного приближения

АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.

Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:

на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).

2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).

3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.

Рис. 2. Структурная схема АЦП последовательного приближения.

Таким образом, АЦП последовательного приближения состоит из следующих узлов:

1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).

2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.

3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.

4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.

Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).

Дельта-сигма АЦП

И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.

Рис.3. Структурная схема сигма-дельта АЦП.

Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».

Рис. 4. Сигма-дельта АЦП как следящая система

Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].

На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).

Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.

Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.

Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.

Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):

Рис. 6. Структурная схема сигма-дельта модулятора

Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.

Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:

Y(s) = X(s)/(s+1) + E(s)s/(s+1)

То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.

Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра

Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.

Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.

Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.

Немного истории

Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.

Рис. 8. Первый патент на АЦП

Рис. 9. АЦП прямого преобразования (1975 г.)

Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.

На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.

Рис. 10. АЦП прямого преобразования (1970 г.)

Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).

Литература

W. Kester. ADC Architectures I: The Flash Converter. Analog Devices, MT-020 Tutorial. www.analog.com/static/imported-files/tutorials/MT-020.pdf
W. Kester. ADC Architectures II: Successive Approximation ADC. Analog Devices, MT-021 Tutorial. www.analog.com/static/imported-files/tutorials/MT-021.pdf
W. Kester. ADC Architectures III: Sigma-Delta ADC Basics. Analog Devices, MT-022 Tutorial. www.analog.com/static/imported-files/tutorials/MT-022.pdf
W. Kester. ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications. Analog Devices, MT-023 Tutorial. www.analog.com/static/imported-files/tutorials/MT-023.pdf

Аналого-цифровые преобразователи

Аналого-цифровые преобразователи (АЦП)

_{Analog-to-Digital convertors (ADC)}

АЦП служит для измерения напряжения, т.е. преобразования аналоговой информации в цифру. Амплитудам в диапазоне V_n + V ставится в соответствие число n. Одной из характеристик АЦП является его разрядность, т.е. количество дискретных значений напряжения, на которые может делиться весь рабочий диапазон входных (анализируемых) напряжений. Когда АЦП используется для амплитудного анализа, число, получаемое на выходе АЦП используется для адресации памяти и называется номером канала, а V — шириной канала. Номер канала несет информацию об амплитудном значении сигнала. Амплитуда в свою очередь связана с измеряемой физической величиной (энергией, временем и т.п.). Максимальное количество каналов связано с разрядностью АЦП. АЦП нередко служат интерфейсом между измерительной аппаратурой и компьютером. (Многоканальные анализаторы, в состав которых входят АЦП, по сути, специализированные ЭВМ.)
Современные АЦП обычно имеют до 14 двоичных разрядов (16384 каналов). В зависимости от требований эксперимента измерения могут производиться при разных диапазонах конверсии (512, 1024 и т.д.) вплоть до максимального, определяемого разрядностью АЦП
Важными характеристиками АЦП, используемых для спектроскопии, являются интегральная и дифференциальная нелинейности.

Рис. 1. Идеальная (сплошная зеленая линия) и реальная функция преобразования АЦП

Интегральная нелинейность I_int характеризует отклонение реальной функции преобразования (штрихпунктир) от идеальной линейной (сплошная линия) (см. рис. 1). Интегральная нелинейность I_int определяется следующим образом

I_int% = 100(V_nom — V_act)/V_max,

где (V_nom — V_act) — максимальное отклонение от линейности.
Дифференциальная нелинейность I_dif характеризует неоднородность ширин каналов АЦП и определяется следующим образом.

I_dif% = 50(W_max — W_min)/W_avg,

где W_max, W_min и W_avg — максимальная, минимальная и средняя ширины каналов.
У качественных АЦП дифференциальная нелинейность ~1%, а интегральная <0.05% при 12-разрядном (4096 каналов) преобразовании.

В промышленной электронике было разработано много методов преобразования аналоговых величин в цифровой код. Однако в ядерной электронике используются только некоторые из них. В основном используются АЦП вилкинсоновского типа и АЦП поразрядного взвешивания. В последнее время в ядерной электронике стали использоваться и параллельные АЦП, входящие в состав цифровых процессоров сигналов.

Рис.

2. Сигналы в АЦП во время измерения.

а)

б)

в)

Рис. 3. Циклы работы АЦП вилкинсоновского типа.

Аналого-цифровой преобразователь вилкинсоновского типа

Принцип работы АЦП вилкинсоновского типа (D.H Wilkinson) основан на преобразовании амплитуда — время. Входной импульс поступает на дискриминатор нижнего уровня, уровень дискриминации которого обычно устанавливается выше уровня шумов (см. рис. 2). Когда уровень входного сигнала достигнет уровня дискриминации, линейные ворота открываются, и накопительная емкость C соединяется с входом (рис. 3а). Начинается заряд емкости до амплитудного значения входного сигнала. Когда емкость зарядится, линейные ворота закрываются, накопительная емкость отсоединяется от входа и присоединяется к источнику постоянного тока (рис. 3б). Начинается линейный разряд емкости. В это же время таймирующий (времязадающий) генератор подключается к адресному счетчику, который начинает считать импульсы таймирующего генератора. Частота генератора обычно 100 — 200 МГц. Когда емкость полностью разрядится, накопительная емкость отсоединяется от источника постоянного тока, а таймирующий генератор отсоединяется от адресного счетчика (рис. 3в) и начинается цикл записи в память. Число сосчитанных во время разряда емкости импульсов определяет время разряда накопительной емкости, а время линейного разряда пропорционально амплитуде анализируемого импульса. Полученное в адресном счетчике число (код) используется для адресации соответствующей ячейки памяти, куда добавляется единица.
Мертвое время у этого АЦП складывается из

= T_r + T_c + T_mc,

где T_r — время достижения максимума импульса, T_c — время конверсии, T_mc — время цикла записи. Времена T_r и T_mc около 1 мкс. Основной вклад в мертвое время вносит время конверсии, которое зависит от амплитуды входного импульса или соответственно от номера канала n (T_c = nT_gen), где T_gen — период таймирующего генератора. Так T_c = 10 мкс при частоте генератора 100 МГц и n = 1000.
У АЦП вилкинсоновского типа малые интегральная и дифференциальная нелинейности, однако относительно большое мертвое время, которое к тому же зависит от амплитуды.

Аналого-цифровой преобразователь поразрядного взвешивания

Successive approximation ADC (Fixed Dead Time ADC)

Принцип работы АЦП поразрядного взвешивания заключается в последовательном сравнении амплитуды анализируемого сигнала (V_in) с напряжением цифро-аналогово преобразователя (V_DAC), уровень которого задается регистром.

Номер канала	Состояние регистра	Диапазон амплитуд
8	000	V_max>V>7/8(V_max)
7	111	7/8(V_max)>V>6/8(V_max)
6	110	6/8(V_max)>V> 5/8(V_max)
5	101	5/8(V_max)>V> 4/8(V_max)
4	100	4/8(V_max)>V> 3/8(V_max)
3	011	3/8(V_max)>V> 2/8(V_max)
2	010	2/8(V_max)>V> 1/8(V_max)
1	001	1/8(V_max)>V

Для простоты рассмотрим работу трехразрядного АЦП. В начальном состоянии в старшем бите регистра установлена единица (100). Согласно этой установке цифро-аналоговый преобразователь (ЦАП) устанавливает напряжение равное половине динамического диапазона (V_DAC = V_max/2). Это напряжение сравнивается с величиной измеряемой амплитуды V_in. Если V_in > V_max/2, то в регистре следующий бит (110), а в ЦАП соответственно устанавливается напряжение 6/8(V_max). Если V_in < V_max/2, то в регистре старший бит зануляется, а единица устанавливается в следующем бите (010), что соответствует напряжению ЦАП 2/8(V_max). После еще одного (третьего) сравнения преобразование заканчивается, при этом |V_in — V_DAC| < V_max/8, а конечное состояние регистра определяет адрес ячейки памяти, куда добавляется единица. В 12-разрядном АЦП (4096 каналов) проводится соответственно 12 сравнений. Время преобразования и, соответственно, мертвое время АЦП поразрядного взвешивания не зависит от амплитуды как в АЦП вилкинсоновского типа, а определяется количеством сравнений, т. е. разрядностью. Мертвое время АЦП поразрядного взвешивания ~1 мкс. Дифференциальная нелинейность таких АЦП несколько хуже, чем у АЦП вилкинсоновского типа.
Улучшить дифференциальную нелинейность можно с помощью метода сдвигающейся шкалы (sliding scale linearization). Его также называют методом статистического разравнивания. Сущность этого метода заключается в следующем. К входному сигналу добавляется ступенька напряжения примерно равная ширине канала, к следующему входному сигналу — удвоенная ступенька и т.д. m раз, после чего система возвращается в исходное состояние*. В адресном регистре каждый раз формируется число, которое на m больше, чем должно было бы быть без добавления «ступенек». Затем из адресного регистра это число m вычитается. Таким образом, происходит статистическое усреднение ширины каналов, и дифференциальная нелинейность уменьшается в (m+1) раз.
__________________________________________________
* Это похоже на измерение расстояний при помощи линейки, нулевая отметка у которой от измерения к измерению сдвигается на одно деление.

Параллельное АЦП

Flash ADC

Успехи микроэлектроники позволили создать параллельные АЦП, с помощью которых можно снимать профили аналоговых сигналов, т.е. получать развертку сигнала во времени в цифрах. В параллельном АЦП содержится большое количество (2^k), где k — разрядность АЦП, параллельно включенных дискриминаторов с последовательно увеличивающимися порогами дискриминации

V_n = V_n-1 + V.

Количество сработавших дискриминаторов собственно и есть результат преобразования аналоговой информации (напряжения) в цифру. Неоспоримым преимуществом таких АЦП является то, что они очень быстрые. Параллельные АЦП в частности нашли применение в цифровых процессорах спектрометрических сигналов. Для большинства применений такие АЦП должны иметь 12 разрядов и оцифровывать с частотой ~100 МГц. Для временных измерений с быстрыми сцинтилляторами требуются 8-разрядные АЦП с частотой ~1 ГГц.

[ОГЛАВЛЕНИЕ]

Измерение значений кажущегося коэффициента диффузии (ADC) опухолей эпендимомы и медуллобластомы: исследование на основе пациентов

1. Arle J E, Morriss C, Wang Z J, Zimmerman R A, Phillips PG, Sutton L N. у детей с помощью свойств магнитно-резонансного изображения, спектроскопии и нейронных сетей. Дж Нейрохирург . 1997; 86: 755–61. doi: 10.3171/jns.1997.86.5.0755. [PubMed] [CrossRef] [Google Scholar]

2. Гупта. МРТ с переносом намагниченности более близка к гистопатологии, чем обычная МРТ при внутричерепных туберкулемах. Материалы восьмого собрания Международного общества магнитного резонанса в медицине Беркли; Калифорния: Международное общество магнитного резонанса в медицине; 2000 [Google Scholar]

3. Poretti A, Meoded A, Huisman TA. Нейровизуализация опухолей задней черепной ямки у детей, включая обзор литературы. J Magn Reson Imaging . 2012; 35:32–47. doi: 10.1002/jmri.22722. [PubMed] [CrossRef] [Google Scholar]

4. Provenzale J M, Mukundan S, Barboriak D P. Диффузионно-взвешенная и перфузионная МРТ для характеристики опухоли головного мозга и оценки ответа на лечение. Радиология . 2006; 239: 632–49. doi: 10.1148/radiol.2393042031. [PubMed] [CrossRef] [Google Scholar]

5. Stadnik T W, Chaskis C, Michotte A, Shabana WM, Van Rompaey K, Luypaert R, et al. Диффузионно-взвешенная МРТ внутримозговых образований: сравнение с обычной МРТ и гистологическими данными. AJNR Am J Нейрорадиол . 2001; 22: 969–76. [Бесплатная статья PMC] [PubMed] [Google Scholar]

6. Sugahara T, Korogi Y, Kochi M, Ikushima I, Shigematu Y, Hirai T, et al. Полезность диффузионно-взвешенной МРТ с эхо-планарной техникой для оценки клеточности глиом. J Magn Reson Imaging . 1999; 9: 53–60. [PubMed] [Google Scholar]

7. Gupta R K, Cloughesy TF, Sinha U, Garakian J, Lazareff J, Rubino G, et al. Взаимосвязь между спектроскопией магнитного резонанса холина, кажущимся коэффициентом диффузии и количественной гистопатологией глиомы человека. J Нейроонкол . 2000; 50: 215–26. [PubMed] [Google Scholar]

8. Guo A C, Cummings T J, Dash RC, Provenzale J M. Лимфомы и астроцитомы высокой степени злокачественности: сравнение диффузии в воде и гистологических характеристик. Радиология . 2002; 224:177–83. doi: 10.1148/radiol.2241010637. [PubMed] [CrossRef] [Google Scholar]

9. Gauvain K M, McKinstry RC, Mukherjee P, Perry A, Neil J J, Kaufman B A, et al. Оценка клеточности опухоли головного мозга у детей с помощью диффузионно-тензорной визуализации. AJR Am J Рентгенол . 2001; 177: 449–54. doi: 10.2214/ajr.177.2.1770449. [PubMed] [CrossRef] [Google Scholar]

10. Tien R D, Felsberg G J, Friedman H, Brown M, MacFall J. МРТ церебральных глиом высокой степени злокачественности: значение диффузионно-взвешенных эхопланарных импульсных последовательностей. AJR Am J Рентгенол . 1994; 162: 671–7. doi: 10.2214/ajr.162.3.8109520. [PubMed] [CrossRef] [Google Scholar]

11. Kono K, Inoue Y, Nakayama K, Shakudo M, Morino M, Ohata K, et al. Роль диффузионно-взвешенной визуализации у пациентов с опухолями головного мозга. AJNR Am J Нейрорадиол . 2001; 22:1081–8. [Бесплатная статья PMC] [PubMed] [Google Scholar]

12. Моррис М. С., Циммерман Р. А., Биланюк Л. Т., Хантер Дж. В., Хазелгроув Дж. К. Изменения диффузии воды в головном мозге в детстве. Нейрорадиология . 1999;41:929–34. [PubMed] [Google Scholar]

13. Sener R N. Диффузионная МРТ: значения кажущегося коэффициента диффузии (ADC) в нормальном мозге и классификация нарушений головного мозга на основе значений ADC. Comput Med Imaging Graph . 2001; 25: 299–326. [PubMed] [Google Scholar]

14. Александр А.Л., Цуруда Дж.С., Паркер Д.Л. Устранение вихретоковых артефактов в диффузионно-взвешенных эхо-планарных изображениях: использование биполярных градиентов. Магн Резон Мед . 1997; 38:1016–21. [PubMed] [Google Scholar]

15. Дитрих О., Биффар А., Баур-Мельник А., Райзер М. Ф. Технические аспекты МР-диффузионной визуализации тела. Евро J Радиол . 2010;76:314–22. doi: 10.1016/j. ejrad.2010.02.018. [PubMed] [CrossRef] [Google Scholar]

16. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. МРТ некогерентных внутривоксельных движений: приложение к диффузии и перфузии при неврологических расстройствах . Радиология . 1986; 161: 401–7. doi: 10.1148/radiology.161.2.3763909. [PubMed] [CrossRef] [Google Scholar]

17. Беренс М.Е., Рутка Дж.Т., Розенблюм М.Л. Эпидемиология, рост и инвазия опухолей головного мозга. Нейрохирург Клиника N Am . 1990; 1:1–18. [PubMed] [Google Scholar]

18. Mardor Y, Roth Y, Ochershvilli A, Spiegelmann R, Tichler T, Daniels D, et al. Предварительное прогнозирование реакции опухолей головного мозга на лучевую терапию с использованием диффузионно-взвешенной МРТ с высоким значением b. Неоплазия . 2004; 6: 136–42. doi: 10.1593/neo.03349. [ Бесплатная статья ЧВК ] [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

19. Sinnaeve D. Уравнение Стейскала–Таннера, обобщенное для любой формы градиента — обзор большинства последовательностей импульсов, измеряющих свободную диффузию. Принципы магнитного резонанса Часть A . 2012;40:39–65. doi: 10.1002/cmr.a.21223. [CrossRef] [Google Scholar]

20. Мохамед Ф.Ф., Исмаил А.А., Хасан Д.И., Эсса В.Е. Роль значения кажущегося коэффициента диффузии (ADC) в дифференциации наиболее распространенных опухолей задней черепной ямки у детей. Египетский журнал радиологии и ядерной медицины . 2013;44:349–55. doi: 10.1016/j.ejrnm.2012.12.011. [CrossRef] [Google Scholar]

21. Rumboldt Z, Camacho D L, Lake D, Welsh CT, Castillo M. Очевидные коэффициенты диффузии для дифференциации опухолей мозжечка у детей. AJNR Am J Нейрорадиол . 2006; 27:1362–9. [PMC free article] [PubMed] [Google Scholar]

22. Uysal F, Çakmakçı H, Yiş U, Ellidokuz H, Hız A S. Измерение кажущегося коэффициента диффузии в педиатрических случаях митохондриальной энцефалопатии и сравнение паренхиматозных изменений, связанных с заболеванием с использованием последующих измерений коэффициента диффузии. Евро J Радиол . 2014;83:212–8. doi: 10.1016/j.ejrad.2013.06.031. [PubMed] [CrossRef] [Google Scholar]

23. Zitouni S, Koc G, Doganay S, Saracoglu S, Gumus KZ, Ciraci S, et al. Кажущийся коэффициент диффузии при дифференциации опухолей задней черепной ямки у детей. Jpn J Radiol . 2017; 35: 448–53. doi: 10.1007/s11604-017-0652-9. [PubMed] [CrossRef] [Google Scholar]

24. Pierce T, Kranz PG, Roth C, Leong D, Wei P, Provenzale JM. Использование значений кажущегося коэффициента диффузии для диагностики опухолей задней черепной ямки у детей. Нейрорадиол J . 2014;27:233–44. doi: 10.15274/NRJ-2014-10027. [ Бесплатная статья ЧВК ] [PMC free article] [PubMed] [CrossRef] [Google Scholar]

25. Коценас А.Л., Рот Т.С., Маннесс В.К., Фаербер Е.Н. Аномальная диффузионно-взвешенная МРТ при медуллобластоме: отражает ли она мелкоклеточную гистологию? Педиатр Радиол . 1999; 29: 524–6. doi: 10.1007/s002470050636. [PubMed] [CrossRef] [Google Scholar]

26. Яремко Дж. Л., Янс Л. Б., Коулман Л. Т., Дитчфилд М. Р. Ценность и ограничения диффузионно-взвешенной визуализации при классификации и диагностике опухолей задней черепной ямки у детей. AJNR Am J Нейрорадиол . 2010;31:1613–6. doi: 10.3174/ajnr.A2155. [PMC free article] [PubMed] [CrossRef] [Google Scholar]

27. Филиппи С.Г., Эдгар М.А., Улуг А.М., Провда Дж.С., Хейер Л.А., Циммерман Р.Д. Внешний вид менингиом на диффузионно-взвешенных изображениях: корреляция констант диффузии с гистологическими находками. AJNR Am J Нейрорадиол . 2001; 22: 65–72. [Бесплатная статья PMC] [PubMed] [Google Scholar]

28. Pillai S, Singhal A, Byrne AT, Dunham C, Cochrane DD, Steinbok P. Диффузионно-взвешенная визуализация и патологическая корреляция при медуллобластомах у детей: «Они не всегда ограниченный!» Чайлдс Нерв Сист . 2011; 27:1407–11. doi: 10.1007/s00381-011-1499-5. [PubMed] [CrossRef] [Google Scholar]

Коэффициент кажущейся диффузии для различения злокачественных и доброкачественных образований в области головы и шеи: систематический обзор и метаанализ

Введение

метод магнитно-резонансной томографии (МРТ), основанный на измерении диффузии воды в тканях (1).

Ограничение диффузии воды можно количественно оценить с помощью кажущегося коэффициента диффузии (ADC) (1). Многочисленные исследования показали, что DWI/ADC может предоставить информацию о гистологической архитектуре тканей. Согласно литературным данным, ADC связан с несколькими гистопатологическими особенностями, такими как количество клеток и экспрессия маркеров пролиферации (2, 3). Таким образом, было показано, что ADC хорошо коррелирует с экспрессией Ki67 при плоскоклеточном раке головы и шеи (4, 5). Кроме того, ADC может предсказать другие важные гистопатологические признаки, такие как экспрессия сосудистого эндотелиального фактора роста, белка-супрессора опухоли p53, фактора, индуцируемого гипоксией (HIF)-1α, количества CD3-позитивных клеток и вируса папилломы человека (p16) (5–6). 7).

Однако в клинических условиях ключевой вопрос заключается в том, можно ли использовать DWI/ADC для различения злокачественных и доброкачественных поражений. В целом хорошо известно, что злокачественные опухоли имеют более низкие значения ADC, чем доброкачественные образования. Однако врачу нужны правдоподобные пороговые значения в его или ее ежедневной практике. Ранее в некоторых отчетах анализировался диагностический потенциал DWI в области головы и шеи (HNR). Тем не менее, в большинстве опубликованных исследований изучались относительно небольшие выборки до 100 пациентов/очагов, и, следовательно, предоставленные данные не могут применяться как очевидные. Кроме того, опубликованные исследования предоставили широкий спектр пороговых значений ADC. Например, Wang et al., основываясь на анализе 97 различных поражений головы и шеи предложили диагностическую шкалу значений ADC для прогнозирования злокачественности при HNR (8). Было показано, что значения ADC ≤0,65 × 10 ^-3 мм ² /с имели положительное прогностическое значение злокачественности 100%, а значения ADC ≤1,01 × 10 ^-3 мм ² /с положительное прогностическое значение злокачественности 90% (8). В исследовании Das et al. при исследовании 79 синоназальных образований пороговое значение ADC 1,791 × 10 ^-3 мм ² /с было определено для дифференциации злокачественных и доброкачественных образований с чувствительностью 80% и специфичностью 83,3% (9). ). Наконец, Ли и соавт. исследовали 78 пациентов с поражениями языка и рассчитали пороговое значение ADC <1,31 × 10 ^-3 мм ² /с (чувствительность 92,6%, специфичность 97,3%) (10).

Цель настоящего метаанализа заключалась в предоставлении данных об использовании ADC для различения злокачественных и доброкачественных поражений в HNR на основе большой выборки.

Материалы и методы

Сбор данных и доказательство

Базы данных MEDLINE и Scopus были проверены на наличие связи между ADC и злокачественностью/доброкачественностью поражений головы и шеи до декабря 2018 г. (рис. 1). Условия поиска/комбинации были следующими:

Рисунок 1 . Блок-схема предпочтительных элементов отчетности для систематических обзоров и метаанализа (PRISMA) сбора данных.

«DWI, или диффузионно-взвешенная визуализация, или диффузионно-взвешенная визуализация, или ADC, или кажущийся коэффициент диффузии, или DWI, или диффузионно-взвешенная визуализация, И голова и шея, ИЛИ карцинома шеи, ИЛИ рак шеи, ИЛИ новообразование шеи, ИЛИ опухоль шеи». Вторичные ссылки также проверялись вручную. В исследовании использовалось заявление о предпочтительных отчетных элементах для систематических обзоров и метаанализов (PRISMA) (11).

Первичной конечной точкой систематического обзора был анализ связи между характером поражений головы и шеи и их значениями ADC. Первичный поиск выявил 239 записей. Тезисы пунктов были проверены. Критерии включения в эту работу были следующими:

— данные относительно ADC, полученные из DWI,

— доступные значения среднего и стандартного отклонения ADC,

— оригинальные исследования, в которых изучались люди, и

— написанные на английском языке.

В целом 22 исследования соответствуют критериям включения (9, 10, 12–31). Остальные 217 записей были исключены из анализа. Критерии исключения были следующими:

— исследования, не связанные с предметами исследований,

— исследования с неполными данными,

— не написанные на английском языке,

— дублирующие публикации,

— экспериментальные животные и исследования in vitro , и

— обзоры, метаанализы и статьи о клинических случаях.

На следующем этапе из литературы были извлечены следующие данные: авторы, год публикации, дизайн исследования, количество пациентов/опухолей, тип опухоли/поражения, среднее значение и стандартное отклонение ADC.

Мета-анализ

Методологическое качество выявленных 22 исследований было проверено в соответствии с инструментом оценки качества исследований диагностической точности (QUADAS) (32) независимо двумя наблюдателями (А.С. и Х.Дж.М.) (рис. 2).

Рисунок 2 . Оценка качества исследований диагностической точности (QUADAS)-2 оценка качества включенных исследований.

Метаанализ был проведен с использованием RevMan (RevMan 2014, Cochrane Collaboration Review Manager, версия 5.3). Неоднородность рассчитывали с помощью индекса несогласованности I ² (33, 34). Модели случайных эффектов ДерСимониана и Лэрда с весами обратной дисперсии использовались без поправок (35). Средние значения ADC, включая 95% доверительные интервалы, рассчитывали отдельно для доброкачественных и злокачественных поражений.

Результаты

Из включенных 22 исследований 14 (64%) были ретроспективными, а 8 (36%) — проспективными. В целом, эти исследования включали 1227 поражений. Различные злокачественные новообразования ГНС диагностированы в 818 случаях (66,7%), доброкачественные образования — в 409.случаев (33,3%) (табл. 1). Средние значения ADC злокачественных образований варьировали от 0,75 до 1,35 × 10 ^-3 мм ² /с, а расчетное среднее значение составило 1,04 × 10 ^-3 мм ² /с (рис. 3).

Таблица 1 . Злокачественные опухоли и доброкачественные образования, участвующие в анализе.

Рисунок 3 . Графики Форреста значений кажущегося коэффициента диффузии (ADC) доброкачественных поражений области головы и шеи.

Расчетное среднее значение доброкачественных образований составило 1,46 × 10 ^-3 мм ² /с, а диапазон собранных значений АЦП составил 0,61-1,95 × 10 ^-3 мм ² /с (рис. 4). Графическое распределение значений ADC при злокачественных и доброкачественных поражениях показано на рисунке 5. Значения ADC значительно перекрываются.

Рисунок 4 . Графики Форреста значений кажущегося коэффициента диффузии (ADC) злокачественных опухолей области головы и шеи.

Рисунок 5 . Сравнение значений кажущегося коэффициента диффузии (ADC) между злокачественными и доброкачественными образованиями.

Кроме того, были проанализированы сообщаемые средние значения ADC для различных злокачественных поражений (рис. 6). Лимфомы и саркомы показали самые низкие расчетные средние значения ADC 0,7 и 0,79 × 10 ^-3 мм ² /с соответственно. Аденоидно-кистозные карциномы имели самые высокие значения ADC (1,5 × 10 ^-3 мм ²/с). Рассчитанные средние значения ADC плоскоклеточного рака и нейробластомы составили 1,09 и 1,02 × 10 ^-3 мм ² /с соответственно. Ни одна из проанализированных злокачественных опухолей не имела средних значений ADC выше 1,75 × 10 ⁻³ мм ² /с.

Рисунок 6 . Сравнение значений кажущегося коэффициента диффузии (ADC) между различными злокачественными образованиями.

Обсуждение

Наш анализ показал, что как злокачественные, так и доброкачественные поражения в HNR представлены широким спектром значений ADC. Хотя у злокачественных опухолей значения ADC были ниже, чем у доброкачественных поражений, сообщаемые значения ADC значительно перекрывались. Этот факт сделал невозможным определение надежного порога различения злокачественного и доброкачественного образования при ГНР. Кроме того, наше открытие может объяснить противоречивые результаты предыдущих исследований. Хорошо известно, что некоторые доброкачественные образования головы/шеи, такие как холестеатомы и гипертрофия аденоидов, имеют очень низкие значения ADC (36, 37), а некоторые опухоли, такие как аденоидно-кистозные карциномы, имеют высокие значения ADC (8, 9).). Предположительно, исследования с разными злокачественными и/или доброкачественными поражениями ГНС могут иметь разные пороговые значения АКД. Этот факт очень важен. Следовательно, анализ значений ADC между злокачественными и доброкачественными поражениями HNR должен включать все возможные объекты.

Мы включили все опубликованные значения ADC для различных поражений HNR в настоящий анализ без предвзятости выбора. Насколько нам известно, наш анализ включает самую большую когорту на сегодняшний день. Мы не смогли найти пороги в нижних областях значений ADC, потому что злокачественные и доброкачественные образования значительно перекрываются. Однако зарегистрированные значения ADC для всех злокачественных новообразований были ниже 1,75 × 10 9 .0121 −3 мм ² /с. Следовательно, можно предположить, что поражения со средними значениями ADC выше 1,75 × 10 ^-3 мм ²/с, вероятно, являются доброкачественными. Наши результаты также показали, что в области <1,75 × 10 90 121 -3 90 122 мм 90 121 2 90 122 /с невозможно найти реальных порогов для различения злокачественных и доброкачественных образований. Кроме того, настоящий анализ показал, что лимфомы и саркомы имели самые низкие средние значения ADC, а аденоидно-кистозные карциномы имели самые высокие значения ADC. Этот вывод согласуется с предыдущими отчетами (8, 38).

В целом, настоящий анализ показал, что только DWI/ADC нельзя использовать в качестве визуализирующего биомаркера злокачественности в HNR. Однако известно, что области с высокой клеточностью и высокой пролиферацией потенциально имеют более низкие значения ADC, чем области с низкой клеточностью, независимо от природы поражения (2, 3). Кроме того, во многих предыдущих отчетах упоминалось, что области некротических опухолей имеют более низкие значения ADC, чем солидные части. Следовательно, области с низкими значениями ADC можно использовать в качестве дополнительной мишени для биопсии.

Наш анализ имеет некоторые ограничения. Во-первых, он основан только на результатах, написанных на английском языке. Во-вторых, он проанализировал технику DWI с использованием 2 b значений. Тем не менее, более продвинутые методы визуализации, такие как внутривоксельная визуализация некогерентного движения и визуализация диффузного эксцесса, которые могли бы показать лучшую точность в различении доброкачественных опухолей от злокачественных, не были включены в анализ. В-третьих, мы не анализировали возможное влияние некоторых технических деталей, таких как тип последовательности, выбор 9значения 0173 b и сила Теслы. Следует также обратить внимание на следующий аспект: ранее некоторые авторы указывали, что значения ADC значительно зависят от измерений ADC (39, 40). Было показано, что различные методы рисования, например, измерение всей опухоли, выбор нескольких областей интереса и/или измерение одной области, могут влиять на значения ADC (39, 40). Следовательно, различные измерения АЦП также следует рассматривать как важный фактор. Однако недавний крупный метаанализ показал, что отношения значений ADC между злокачественными и доброкачественными образованиями молочной железы не зависят от метода и измерений МРТ (41).

В целом, наш анализ основан на гетерогенных и преимущественно ретроспективных выборках. Однако он отражает реальную клиническую ситуацию в повседневной жизни.

В заключение, наш анализ показал, что значения ADC играют ограниченную роль в различении злокачественных и доброкачественных поражений в HNR.

Поражения со средними значениями ADC выше 1,75 × 10 ^-3 мм ²/с, вероятно, доброкачественные. Необходимы дальнейшие крупные исследования для анализа роли DWI/ADC в различении доброкачественных и злокачественных поражений в HNR.

Вклад авторов

Все перечисленные авторы внесли существенный, непосредственный и интеллектуальный вклад в работу и одобрили ее для публикации.

Конфликт интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Сокращения

HNR, область головы и шеи; МРТ, магнитно-резонансная томография; ADC, кажущийся коэффициент диффузии.

Ссылки

1. Fornasa F. Диффузионно-взвешенная магнитно-резонансная томография: что заставляет воду течь быстрее или медленнее? J Clin Imaging Sci. (2011) 1:27. doi: 10.4103/2156-7514.81294

Полный текст CrossRef | Google Scholar

2. Суров А., Мейер Х.Дж., Винке А. Корреляция между кажущимся коэффициентом диффузии (ADC) и клеточностью различается в нескольких опухолях: метаанализ. Онкотаргет. (2017) 8:59492–9. doi: 10.18632/oncotarget.17752

Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar

3. Суров А., Мейер Х.Дж., Винке А. Корреляция между кажущимся коэффициентом диффузии (ADC) и KI 67 в различных опухолях: метаанализ. Часть 1: среднее значение АЦП. Онкоцель . (2017) 8:75434–44. doi: 10.18632/oncotarget.20406

Полный текст CrossRef | Google Scholar

4. Суров А., Штумпп П., Мейер Х.Дж., Гавлица М., Хён А.К., Бем А. и др. Одновременная (18) F-FDG-PET/MRI: связь между диффузией, метаболизмом глюкозы и гистопатологическими параметрами у пациентов с плоскоклеточным раком головы и шеи. Оральная онкология. (2016) 58:14–20. doi: 10.1016/j.oraloncology.2016.04.009

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

5. Swartz JE, Driessen JP, van Kempen PMW, de Bree R, Janssen LM, Pameijer FA, et al. Влияние характеристик опухоли и микроокружения на диффузионно-взвешенную визуализацию рака ротоглотки: пилотное исследование. Оральная онкология. (2018) 77:9–15. doi: 10.1016/j.oraloncology.2017.12.001

PubMed Abstract | Полный текст перекрестной ссылки | Академия Google

6. Meyer HJ, Leifels L, Hamerla G, Höhn AK, Surov A. Анализ ADC-гистограммы при плоскоклеточном раке головы и шеи. Ассоциации с различными гистопатологическими особенностями, включая экспрессию EGFR, VEGF, HIF-1α, Her 2 и p53. Предварительное исследование. Magn Reson Imaging. (2018) 54:214–7 doi: 10.1016/j.mri.2018.07.013

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

7. Суров А., Мейер Х.Дж., Винке А. Могут ли параметры визуализации предоставить информацию о гистопатологии плоскоклеточного рака головы и шеи? Метаанализ. Пер. Онкол. (2018) 11: 498–503. doi: 10.1016/j.tranon.2018.02.004

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

8. Ван Дж., Такашима С., Такаяма Ф., Каваками С., Сайто А., Мацусита Т. и др. Поражения головы и шеи: характеристика с помощью диффузионно-взвешенной эхо-планарной МРТ. Радиология. (2001) 220:621–30. doi: 10.1148/radiol.2202010063

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

9. Дас А., Бхалла А.С., Шарма Р., Кумар А., Такар А., Вишнубхатла С.М. и др. Может ли диффузионно-взвешенная визуализация помочь в дифференциации доброкачественных образований синоназа от злокачественных? Полезное дополнение. Pol J Радиол. (2017) 82:345–55. doi: 10.12659/PJR.3