
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи:
^ .
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».
Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .
Таблица истинности:
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a ^ b = |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Wikimedia Foundation. 2010.
dic.academic.ru
Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только приA=1 и B=1.
Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.
Определение данной операции может быть записано в виде таблицы истинности (таблица 6):
Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»
Х1 | Х2 | Y |
1 | 1 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 0 |
Как видно из таблицы 6, логика работы элемента соответствует его названию.
Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.
Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).
Таблица 7 – Основные логические операции
Обозначение операции | Читается | Название операции | Альтернативные обозначения |
¬ | НЕ | Отрицание (инверсия) | Черта сверху |
^ | И | Конъюнкция (логическое умножение) | & |
v | ИЛИ | Дизъюнкция (логическое сложение) | + |
→ | Если … то | Импликация | |
↔ | Тогда и только тогда | Эквиваленция | ~ |
XOR | Либо … либо | ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2) | |
Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.
При вычислении значения логического выражения принят определённый порядок выполнения логических операций.
1. Инверсия.
2. Конъюнкция.
3. Дизъюнкция.
4. Импликация.
5. Эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «(2·2=5 или 2∙2=4) и (2∙2≠5 или 2∙2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0),
В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме:
«(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В
нашем случае логическая функция 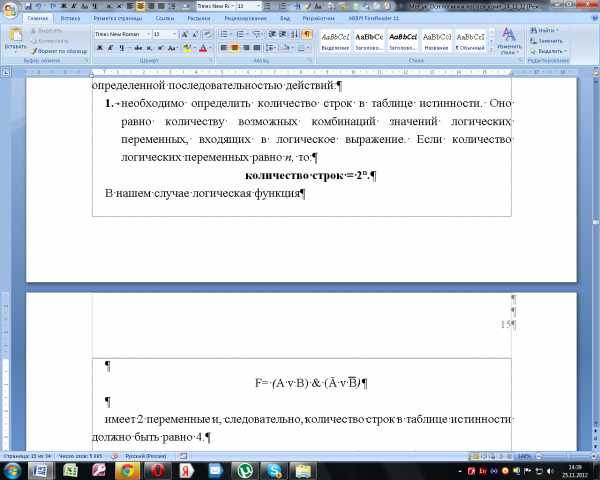
имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
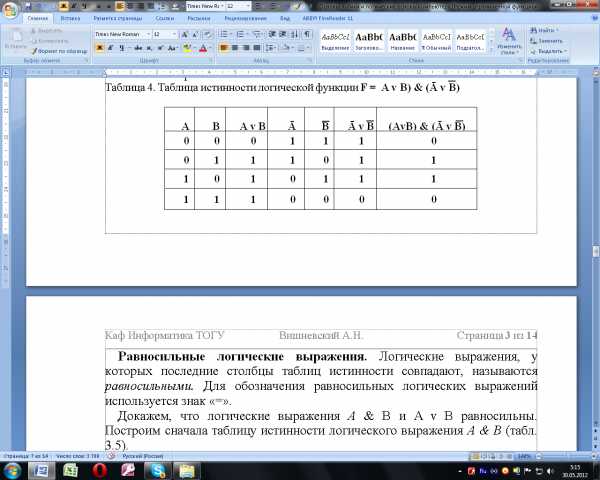
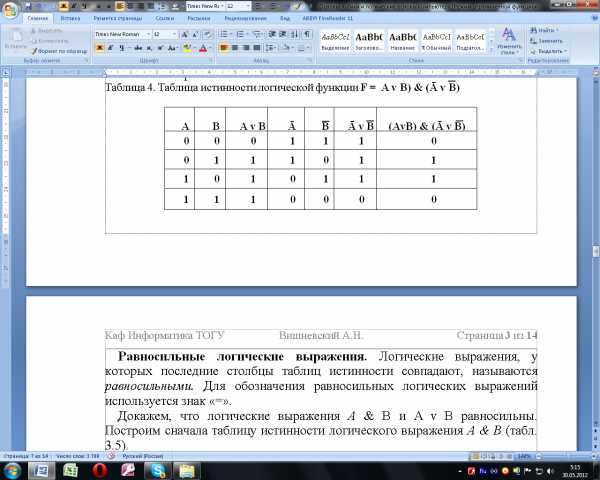
Таблица 8 – Таблица истинности логической функции
studfiles.net
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи:
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».
Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .
Таблица истинности:
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a ^ b = |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Wikimedia Foundation. 2010.
dvc.academic.ru
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи:
^ .
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина».
Правило: результат равен , если оба операнда равны; во всех остальных случаях результат равен .
Таблица истинности:
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a ^ b = |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Wikimedia Foundation. 2010.
dic.academic.ru
Везде ищу так и не понял, что значит эта операция! Кто может обясните по простому, что это такое и как этим пользоваться!
жди Ю.З. только у него терпения на это хватает.
http://ru.wikipedia.org/wiki/XOR
Исключающее или.
X Y
0 0 - False
0 1 - True
1 0 - True
1 1 - False
Сравни с OR0 0 - False
0 1 - True
1 0 - True
1 1 - True
Те ИСТИНА будет только если X и Y — РАЗНЫЕ
1 xor 1 = 0
1 xor 0 = 1
0 xor 1 = 1
0 xor 0 = 0
т.е. true, когда строго один из операндов true
одна из фишек xor, это то, что
(B xor A) xor A = B
эдакий простенький способ шифрования.
кстати единственный (если не ошибаюсь) принципиально не взламываемый, если
1. длина ключа = длине шифруемых данных.
2. содержимое ключа содержит случайные байты.
как все хотят прослыть учителями то 🙂
> Ketmar © (11.08.06 01:32) [1]
>
> жди Ю.З. только у него терпения на это хватает.
>
Не. Не только ЮЗ. Советую автору почитать А.П. http://www.delphikingdom.com/asp/viewitem.asp?catalogid=838
для запоминание, на первых порах, можно представлять что это вычитание взятое по модулю. |A — B|
> [7] ferr © (11.08.06 02:06)
> для запоминание, на первых порах, можно представлять что
> это вычитание взятое по модулю. |A — B|
Не надо. Это сразу и надолго будет не то.
> ferr © (11.08.06 02:06) [7]
>
> для запоминание, на первых порах,
Для «запоминания, на первых порах» я, лично, помню только одно:
Чтобы нам не ошибаться,
Надо правильно прочесть.
Три, четырнадцать, пятнадцать,
девяносто два и шесть.
Каждый курсант обязан знать и уметь грамотно применять исключающее или, или как говорим мы, военные моряки — ксорить. В условиях военного времени, за недоксоривание полагается расстрел на месте.
¬ (a <=> b)
Возьми калькулятор виндовс, посчитай, прими как данность. тайный смысл ищешь, автор?
> [4] Суслик © (11.08.06 01:34)
ошибаетесь.
по-человечески говоришь?
если (Катя зайдёт сегодня за мной блондинкой) или (Катя зайдёт сегодня за мной шатенкой), то я пойду с ней гулять
понятно, что оба условия одновременно быть выполнены не могут
то есть мы идём гулять только когда какое-то одно условие выполнено
можешь считать таблицу истинности xor как формализацию логики таких условных предложений естественного языка
> vidiv © (11.08.06 06:23) [11]
Почему же с отрицанием?
> default © (11.08.06 10:28) [14]
> если (Катя зайдёт сегодня за мной блондинкой) или (Катя
> зайдёт сегодня за мной шатенкой), то я пойду с ней гулять
>
> понятно, что оба условия одновременно быть выполнены не
> могут
А если Катя только полбашки покрасит в блондинку?
DrPass © (11.08.06 10:49) [16]
> default © (11.08.06 10:53) [17]
Просто шутка и никакого буквоедства 😉
> DrPass © (11.08.06 10:49) [16]
Топайте, батенька, в тему про миллибит… 😉
http://kvant.mccme.ru/1975/01/s_chego_nachinaetsya_logika.htm
можно ещё вот это почитать
По-человечески. XOR имеет в русском языке аналог и это — «либо».
Пример.
Процессоры либо видеокарты.
Если в договоре написано, что фирма обязуется в счёт чего-то там поставить на предприятие 100 едениц процессоров либо видеокарт. То это означает, что если на фирме есть 50 процёв и 50 видюх, то по-договору они не могут поставить их на предприятие, т.к. «либо то либо то, но не оба вместе».
DrPass ©
А если Катя только полбашки покрасит в блондинку?
а если Катя будет вовсе не Катя, а Вася, который называет себя в тырнете Катей? это уже не ксор, это просто ужос!
> [22] старый маразматик(с) (11.08.06 11:13)
> а если Катя будет вовсе не Катя, а Вася, который называет
> себя в тырнете Катей? это уже не ксор, это просто ужос!
Это не ксор, это позор…
> Каждый курсант обязан знать и уметь грамотно применять исключающее
> или, или как говорим мы, военные моряки — ксорить. В условиях
> военного времени, за недоксоривание полагается расстрел
> на месте.
Это из серии: в военное время значение числа PI может достигать четырех? 🙂
> в военное время значение числа PI может достигать четырех?
> 🙂
В военное время значение числа PI является государственной военной тайной.
> > vidiv © (11.08.06 06:23) [11]
>
> Почему же с отрицанием?
Потому, что результат операции XOR есть «истина», только тогда, когда операнды не равны.
delphimaster.net
Обновл. 26 мая 2019 |
Примечание: Для некоторых этот материал может показаться сложным. Если вы застряли или что-то не понятно — пропустите этот урок (и следующий), в будущем сможете вернуться и разобраться детальнее. Он не столь важен для прогресса в изучении C++, как другие уроки, и изложен здесь в большей мере для общего развития.
Побитовые операторы манипулируют отдельными битами в пределах переменной.
В далёком прошлом компьютерной памяти было очень мало и ею сильно дорожили. Это было стимулом максимально разумно использовать каждый доступный бит. Например, в логическом типе данных bool есть всего лишь два возможных значения (true и false), которые могут быть представлены одним битом, но по факту занимают целый байт памяти! А это, в свою очередь, из-за того, что переменные используют уникальные адреса памяти, а они выделяются только в байтах. Переменная bool занимает 1 бит, а другие 7 тратятся впустую.
Используя побитовые операторы, можно создавать функции, которые позволят уместить 8 значений типа bool в переменной размером 1 байт, что значительно сэкономит потребление памяти. В прошлом такой трюк был очень популярен. Но сегодня, по крайней мере, в прикладном программировании, это не так.
Теперь памяти существенно больше и программисты обнаружили, что лучше писать код так, чтобы было проще и понятнее его поддерживать, нежели усложнять его ради незначительной экономии памяти. Поэтому спрос на использование побитовых операторов несколько спал, за исключением случаев, когда необходима ну уже максимальная оптимизация (например: научные программы, которые используют огромное количество данных; игры, где манипуляции с битами могут быть использованы для дополнительной скорости; встроенные программы, где память по-прежнему ограничена).
Есть 6 побитовых операторов:
| Оператор | Символ | Пример | Операция |
| Побитовый сдвиг влево | << | x << y | Все биты в x смещаются влево на y бит |
| Побитовый сдвиг вправо | >> | x >> y | Все биты в x смещаются вправо на y бит |
| Побитовое НЕ | ~ | ~x | Все биты в x меняются на противоположные |
| Побитовое И | & | x & y | Каждый бит в x И каждый бит в y |
| Побитовое ИЛИ | | | x | y | Каждый бит в x ИЛИ каждый бит в y |
| Побитовое исключающее ИЛИ (XOR) | ^ | x ^ y | Каждый бит в x XOR каждый бит в y |
В побитовых операциях следует использовать только целочисленные типы данных unsigned, так как C++ не всегда гарантирует корректную работу побитовых операторов с целочисленными типами signed.
Правило: При работе с побитовыми операторами используйте целочисленные типы данных unsigned.
Примечание: В следующих примерах мы будем работать с 4-битными двоичными значениями.
В C++ количество используемых бит основывается на размере типа данных (в 1 байте находятся 8 бит). Оператор побитового сдвига влево (<<) сдвигает биты влево. Левый операнд является выражением, в котором они сдвигаются, а правый — на сколько мест нужно сдвинуть. Поэтому в выражении 3 << 1 мы имеем в виду «сдвинуть биты влево в литерале 3 на одно место».
Рассмотрим число 3, что в двоичной системе = 0011:
3 = 0011
3 << 1 = 0110 = 6
3 << 2 = 1100 = 12
3 << 3 = 1000 = 8
В последнем третьем случае, один бит перемещается за пределы самого литерала! Биты, сдвинутые за пределы двоичного числа, теряются навсегда.
Оператор побитового сдвига вправо (>>) сдвигает биты вправо. Например:
12 = 1100
12 >> 1 = 0110 = 6
12 >> 2 = 0011 = 3
12 >> 3 = 0001 = 1
В третьем случае мы снова переместили бит за пределы литерала. Он также потерялся навсегда.
Хотя в примерах выше мы смещаем биты в литералах, мы также можем смещать биты и в переменных:
unsigned int x = 4; x = x << 1; // x должен быть 8
unsigned int x = 4; x = x << 1; // x должен быть 8 |
Следует помнить, что результаты операций с побитовыми сдвигами в разных компиляторах могут отличаться.
И для этого тоже.
Сейчас польза от использования побитовых операторов не так велика, как это было раньше. Сейчас в большинстве случаев оператор побитового сдвига влево используется для вывода данных. Например, рассмотрим следующую программу:
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; }
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; } |
Результат выполнения программы выше:
8
А как компилятор понимает, когда нужно применить оператор побитового сдвига влево, а когда выводить данные? Всё очень просто. std::cout переопределяет значение оператора << по умолчанию на новое (вывод данных в консоль). Когда компилятор видит, что левым операндом оператора << является std::cout, то он понимает, что должен произойти вывод данных. Если левым операндом является переменная целочисленного типа данных, то компилятор понимает, что должен произойти побитовый сдвиг влево (операция по умолчанию).
Побитовый оператор НЕ (~), пожалуй, самый простой для объяснения и понимания. Он просто меняет каждый бит на противоположный, например: с 0 на 1 или с 1 на 0. Обратите внимание, результаты побитового НЕ зависят от размера типа данных!
Предположим, что размер типа данных составляет 4 бита:
4 = 0100
~ 4 = 1011 (двоичное) = 11 (десятичное)
Предположим, что размер типа данных составляет 8 бит:
4 = 0000 0100
~ 4 = 1111 1011 (двоичное) = 251 (десятичное)
Побитовые операторы И (&) и ИЛИ (|) работают аналогично логическим операторам И и ИЛИ. Однако, побитовые операторы применяются к каждому биту отдельно! Например, рассмотрим выражение 5 | 6. В двоичной системе это 0101 | 0110. В любой побитовой операции операнды лучше всего размещать следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
А затем применять операцию к каждому столбцу с битами по отдельности. Как вы помните, логическое ИЛИ возвращает true (1), если один из двух или оба операнды истинны (1). Таким макаром работает и побитовое ИЛИ. Выражение 5 | 6 обрабатывается следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
-------
0 1 1 1 // 7
Результат:
0111 (двоичное) = 7 (десятичное)
Также можно обрабатывать и комплексные выражения ИЛИ, например, 1 | 4 | 6. Если хоть один бит в столбце равен 1, то результат целого столбца — 1. Например:
0 0 0 1 // 1
0 1 0 0 // 4
0 1 1 0 // 6
--------
0 1 1 1 // 7
Результатом 1 | 4 | 6 является десятичное 7.
Побитовое И работает аналогично логическому И: возвращается true, только если оба бита в столбце равны 1. Рассмотрим выражение 5 & 6:
0 1 0 1 // 5
0 1 1 0 // 6
--------
0 1 0 0 // 4
Также можно решать и комплексные выражения И, например, 1 & 3 & 7. Только при условии, что все биты в столбце равны 1, результатом столбца будет 1.
0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 0 0 1 // 1
Последний оператор — побитовое исключающее ИЛИ (^) (англ. «XOR» от «eXclusive OR«). При обработке двух операндов, исключающее ИЛИ возвращает true (1), только если один и только один из операндов является истинным (1). Если таких нет или все операнды равны 1, то результатом будет false (0). Рассмотрим выражение 6 ^ 3:
0 1 1 0 // 6
0 0 1 1 // 3
-------
0 1 0 1 // 5
Также можно решать и комплексные выражения XOR, например, 1 ^ 3 ^ 7. Если единиц в столбце чётное количество, то результат — 0. Если нечётное количество, то результат — 1. Например:
0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 1 0 1 // 5
Как и в случае с арифметическими операторами присваивания, C++ предоставляет побитовые операторы присваивания для облегчения внесения изменений в переменные.
| Оператор | Символ | Пример | Операция |
| Присваивание с побитовым сдвигом влево | <<= | x <<= y | Сдвигаем биты в x влево на y бит |
| Присваивание с побитовым сдвигом вправо | >>= | x >>= y | Сдвигаем биты в x вправо на y бит |
| Присваивание с побитовой операцией ИЛИ | |= | x |= y | Присваивание результата выражения x | y переменной x |
| Присваивание с побитовой операцией И | &= | x &= y | Присваивание результата выражения x & y переменной x |
| Присваивание с побитовой операцией исключающего ИЛИ | ^= | x ^= y | Присваивание результата выражения x ^ y переменной x |
Например, вместо х = х << 1; мы можем написать х <<= 1;.
При работе с побитовыми операторами (используя метод столбца) не забывайте о том, что:
При вычислении побитового ИЛИ, если хоть один из битов в столбце равен 1, то результат целого столбца — 1.
При вычислении побитового И, если все биты в столбце равны 1, то результат целого столбца — 1.
При вычислении побитового исключающего ИЛИ (XOR), если единиц в столбце нечётное число, то результат — 1.
1. Какой результат 0110 >> 2 в двоичной системе?
2. Какой результат 5 | 12 в десятичной системе?
3. Какой результат 5 & 12 в десятичной системе?
4. Какой результат 5 ^ 12 в десятичной системе?
Ответ №1
Результатом 0110 >> 2 является двоичное 0001.
Ответ №2
Выражение 5 | 12:
0 1 0 1
1 1 0 0
--------
1 1 0 1 // 13 (десятичное)
Ответ №3
Выражение 5 & 12:
0 1 0 1
1 1 0 0
--------
0 1 0 0 // 4 (десятичное)
Ответ №4
Выражение 5 ^ 12:
0 1 0 1
1 1 0 0
--------
1 0 0 1 // 9 (десятичное)
Оценить статью:
Загрузка…За репост +20 к карме и моя благодарность!
ravesli.com
Большой англо-русский и русско-английский словарь. 2001.
исключающее ИЛИ — Логический оператор Функция «ИСКЛЮЧАЮЩЕЕ ИЛИ» (XOR) равна единице, если равен единице ТОЛЬКО один ее аргумент (МСЭ Т Н.235.0, МСЭ T H.235.6, МСЭ Т Н.235). [http://www.iks media.ru/glossary/index.html?glossid=2400324] операция… … Справочник технического переводчика
Исключающее ИЛИ — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
Исключающее «или» — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
Исключающее или — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
Битовая операция — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Битовая операция (теория алгоритмов) — У этого термина существуют и другие значения, см. Битовая операция (значения). Битовая операция (теория алгоритмов) в теории алгоритмов, криптографии запись знаков 0, 1, плюс, минус, скобка; сложение, вычитание и умножение двух битов (числа… … Википедия
Битовые операции — Не следует путать с булевой функцией. Битовая операция в программировании некоторые операции над цепочками битов. В программировании, как правило, рассматриваются лишь некоторые виды этих операций: логические побитовые операции и… … Википедия
ЭЛЕКТРОННЫЕ СХЕМЫ — графические изображения и элементы многочисленных и разнообразных приборов и устройств электроники, автоматики, радио и вычислительной техники. Проектирование и разработка базовых электронных схем и создаваемых из них более сложных систем как раз … Энциклопедия Кольера
Код Грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея система счисления, в которой два соседних значения… … Википедия
JH — Криптографическая хеш функция Название JH Разработчик У Хунцзюнь (англ Wu Hongjun) Опубликован 16 января 2011 года Размер хеша 224, 256, 384, 512 Число раундов 42 JH семейство из четырех криптографических хеш функций: JH 224, JH 256, JH 384 и JH … Википедия
Булевы операции — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
dic.academic.ru