
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП разрядность измеряется в битах. Разрядностью АЦП определяется и его разрешение- минимальное изменение величины входного аналогового сигнала, которое может быть зафиксировано данным АЦП. АЦП преобразовывает сигнал (напряжение) находящийся в диапазоне измеряемых сигналов. Нижняя и верхняя граница этого диапазона определяются напряжениями, поданными на соответствующие выводы. Для микроконтроллера (МК) со встроенным АЦП, нижняя граница — это уровень GND (0 В), а верхняя — подается на отдельный вывод (AREF- Analog Reference) или используются внутренние источники опорных напряжений. При диапазоне входных напряжений от 0 В до 5 В и использовании 10-битного АЦП мы имеем следующее разрешение АЦП (см. рисунок 3). Т. е. АЦП в состоянии различить сигналы которые отличаются на 4,9 мВ. При увеличении сигнала на 4,9 мВ — результат преобразования увеличится на 1. Если для такого же диапазона входных сигналов использовать АЦП с большей разрядностью, то можно зафиксировать меньшие значения, т.е. получить более точное значение сигнала (на рисунке 4 представлены значения при использовании 24-битного АЦП). При отсутствии различного рода ошибок, разрядность АЦП определяет теоретически возможную точность АЦП. На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (Effective Number Of Bits- ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум.
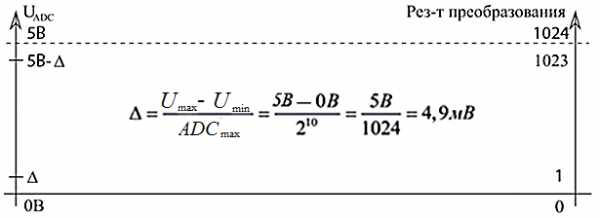
Рисунок 3 — Разрешение 10-битного АЦП
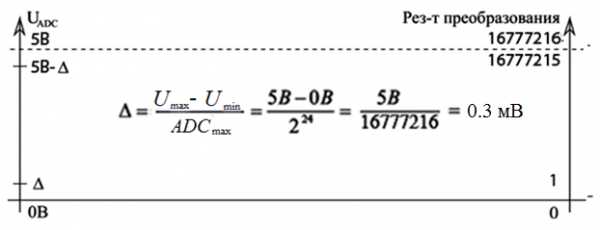
Рисунок 4 — Разрешение 24-битного АЦП
Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5Г (5 * 109) отсчетов/сек для стандартных устройств и 20Г отсчетов/сек для оригинальных разработок. Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10-ти разрядные версии.
Рисунок 5 показывает упрощенную блок-схему 3-х разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется).
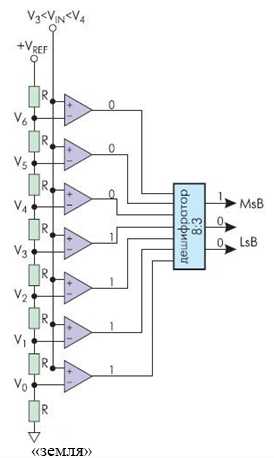
Рисунок 5 — АЦП параллельного преобразования
Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным VREF /2 (Vref- опорное напряжение). В результате для 3-х разрядного АЦП требуется 23 — 1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (28 — 1)) компараторов.
С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рисунке 5 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе «1», а верхние три компаратора — «0». Дешифратор преобразует (2 3 — 1) — разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код.
Состояния компараторов и выходной сигнал в зависимости от уровня входного напряжения можно увидеть в таблице 1.
Таблица 1 — Состояние компараторов и выходные сигналы АЦП
Входное напряжение | Входы дешифраторов (Д) | Выходы Д | |||||||||
Uвx/Q | К7 | К | К5 | К4 | К3 | К2 | K1 | Q2 | Q1 | Q2 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | |
3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||
4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
5 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 6 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
Способ параллельного кодирования обеспечивает наибольшую скорость преобразования, из-за чего его иногда называют способом «мгновенного кодирования». И действительно, время преобразования здесь — всего один такт, и ограничено оно лишь быстродействием компараторов и задержкой на шифраторе.
Для того, чтобы схема могла работать с биполярным сигналом, в месте подключения «земли» (рисунок 5) подключается отрицательное опорное напряжение — Uоп. В состав параллельных АЦП входит большое число компараторов с разным быстродействием, то для синхронизации моментов формирования выходного кода шифратор стробируют сигналом частоты дискретизации (рисунок 6).
studfiles.net
Четырёхканальный аналого-цифровой преобразователь
Аналого-цифровой преобразователь (АЦП, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (DAC) (цифро-аналогового преобразователя).
Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типы преобразователей угол-код.
Аналого-цифровое преобразование электрических сигналов подобно взвешиванию груза на рычажных весах. Итальянский математик Фибоначчи (1170—(1228—1250)) сформулировал задачу наименьшего числа гирь для взвешивания грузов наибольшего диапазона на рычажных весах, которая стала известна под названием «задача о гирях». Решив эту задачу, Фибоначчи пришёл к выводу, что наименьшее число гирь получается при выборе весов гирь в позиционной симметричной троичной системе счисления. Из этого следует, что наиболее оптимальными аналого-цифровыми преобразователями являются аналого-цифровые преобразователи, работающие в позиционной симметричной троичной системе счисления. Из этого следует также вывод, что «электронное взвешивание» намного отстаёт от механического взвешивания, в котором к позиционной симметричной троичной системе счисления пришли ещё в XII веке. Математика «электронного взвешивания» находится ниже уровня математики механического взвешивания XII века. Следует также отметить, что Фибоначчи в своей задаче не учитывал число взвешиваний. При учёте числа взвешиваний (числа итераций при «электронном взвешивании») оказывается, что наименьшее число взвешиваний (итераций) также происходит при выборе позиционной симметричной троичной системы счисления.
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП. Обычно измеряется в вольтах, поскольку для большинства АЦП входным сигналом является электрическое напряжение. В случае единичного измерения без учёта шумов разрешение напрямую зависит от разрядности АЦП.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. Измеряется в битах. Например, АЦП, способный выдать 256 дискретных значений (0..255), имеет разрядность 8 бит, поскольку 28 = 256.
Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений. Например:
На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (effective number of bits — ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. Для достижения заявленной разрядности отношение С/Ш входного сигнала должно быть примерно 6 дБ на каждый бит разрядности.
Большинство АЦП считаются линейными, хотя аналого-цифровое преобразование по сути является нелинейным процессом (поскольку операция отображения непрерывного пространства в дискретное — операция нелинейная). Термин линейный применительно к АЦП означает, что диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением, то есть выходное значение k достигается при диапазоне входных значений от
до
где m и b — некоторые константы. Константа b, как правило, имеет значение 0 или −0.5. Если b = 0, АЦП называют квантователь с ненулевой ступенью (mid-rise), если же b = −0,5, то АЦП называют квантователь с нулём в центре шага квантования (mid-tread).
Если бы плотность вероятности амплитуды входного сигнала имела равномерное распределение, то отношение сигнал/шум (применительно к шуму квантования) было бы максимально возможным. По этой причине обычно перед квантованием по амплитуде сигнал пропускают через безынерционный преобразователь, передаточная функция которого повторяет функцию распределения самого сигнала. Это улучшает достоверность передачи сигнала, так как наиболее важные области амплитуды сигнала квантуются с лучшим разрешением. Соответственно, при цифро-аналоговом преобразовании потребуется обработать сигнал функцией, обратной функции распределения исходного сигнала.
Это тот же принцип, что и используемый в компандерах, применяемых в магнитофонах и различных коммуникационных системах, он направлен на максимизацию энтропии. (Не путать компандер с компрессором!)
Например, голосовой сигнал имеет лапласово распределение амплитуды. Это означает, что окрестность нуля по амплитуде несёт больше информации, чем области с большей амплитудой. По этой причине логарифмические АЦП часто применяются в системах передачи голоса для увеличения динамического диапазона передаваемых значений без изменения качества передачи сигнала в области малых амплитуд.
8-битные логарифмические АЦП с a-законом или μ-законом обеспечивают широкий динамический диапазон и имеют высокое разрешение в наиболее критичном диапазоне малых амплитуд; линейный АЦП с подобным качеством передачи должен был бы иметь разрядность около 12 бит.
Имеется несколько источников погрешности АЦП. Ошибки квантования и (считая, что АЦП должен быть линейным) нелинейности присущи любому аналого-цифровому преобразованию. Кроме того, существуют так называемые апертурные ошибки которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта).
Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд. В приведённом выше примере 8-битного АЦП ошибка в 1 МЗР составляет 1/256 от полного диапазона сигнала, то есть 0,4 %.
Ошибки квантования являются следствием ограниченного разрешения АЦП. Этот недостаток не может быть устранён ни при каком типе аналого-цифрового преобразования. Абсолютная величина ошибки квантования при каждом отсчёте находится в пределах от нуля до половины МЗР.
Как правило, амплитуда входного сигнала много больше, чем МЗР. В этом случае ошибка квантования не коррелирована с сигналом и имеет равномерное распределение. Её среднеквадратическое значение совпадает с среднеквадратичным отклонением распределения, которое равно . В случае 8-битного АЦП это составит 0,113 % от полного диапазона сигнала.
Всем АЦП присущи ошибки, связанные с нелинейностью, которые являются следствием физического несовершенства АЦП. Это приводит к тому, что передаточная характеристика (в указанном выше смысле) отличается от линейной (точнее от желаемой функции, так как она не обязательно линейна). Ошибки могут быть уменьшены путём калибровки.
Важным параметром, описывающим нелинейность, является интегральная нелинейность (INL) и дифференциальная нелинейность (DNL).
Пусть мы оцифровываем синусоидальный сигнал x(t) = Asin2πf0t. В идеальном случае отсчёты берутся через равные промежутки времени. Однако в реальности время момента взятия отсчёта подвержено флуктуациям из-за дрожания фронта синхросигнала (clock jitter). Полагая, что неопределённость момента времени взятия отсчёта порядка Δt, получаем, что ошибка, обусловленная этим явлением, может быть оценена как
Легко видеть, что ошибка относительно невелика на низких частотах, однако на больших частотах она может существенно возрасти.
Эффект апертурной погрешности может быть проигнорирован, если её величина сравнительно невелика по сравнению с ошибкой квантования. Таким образом, можно установить следующие требования к дрожанию фронта сигнала синхронизации:
где q — разрядность АЦП.
| Разрядность АЦП | Максимальная частота входного сигнала | ||||
|---|---|---|---|---|---|
| 44,1 кГц | 192 кГц | 1 МГц | 10 МГц | 100 МГц | |
| 8 | 28,2 нс | 6,48 нс | 1,24 нс | 124 пс | 12,4 пс |
| 10 | 7,05 нс | 1,62 нс | 311 пс | 31,1 пс | 3,11 пс |
| 12 | 1,76 нс | 405 пс | 77,7 пс | 7,77 пс | 777 фс |
| 14 | 441 пс | 101 пс | 19,4 пс | 1,94 пс | 194 фс |
| 16 | 110 пс | 25,3 пс | 4,86 пс | 486 фс | 48,6 фс |
| 18 | 27,5 пс | 6,32 пс | 1,21 пс | 121 фс | 12,1 фс |
| 24 | 430 фс | 98,8 фс | 19,0 фс | 1,9 фс | 190 ас |
Из этой таблицы можно сделать вывод о целесообразности применения АЦП определённой разрядности с учётом ограничений, накладываемых дрожанием фронта синхронизации (clock jitter). Например, бессмысленно использовать прецизионный 24-битный АЦП для записи звука, если система распределения синхросигнала не в состоянии обеспечить ультрамалой неопределённости.
Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала. Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП.
Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации) и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции. Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова-Шеннона точное восстановление возможно только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала.
Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным по крайней мере от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения — УВХ. УВХ, как правило, хранит входное напряжение в конденсаторе, который соединён со входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение. Многие АЦП, выполненные в виде интегральных микросхем содержат встроенное УВХ.
Все АЦП работают путём выборки входных значений через фиксированные интервалы времени. Следовательно, выходные значения являются неполной картиной того, что подаётся на вход. Глядя на выходные значения, нет никакой возможности установить, как себя вёл входной сигнал между выборками. Если известно, что входной сигнал меняется достаточно медленно относительно частоты дискретизации, то можно предположить, что промежуточные значения между выборками находятся где-то между значениями этих выборок. Если же входной сигнал меняется быстро, то никаких предположений о промежуточных значениях входного сигнала сделать нельзя, а следовательно, невозможно однозначно восстановить форму исходного сигнала.
Если последовательность цифровых значений, выдаваемая АЦП, где-либо преобразуется обратно в аналоговую форму цифро-аналоговым преобразователем, желательно, чтобы полученный аналоговый сигнал был максимально точной копией исходного сигнала. Если входной сигнал меняется быстрее, чем делаются его отсчёты, то точное восстановление сигнала невозможно, и на выходе ЦАП будет присутствовать ложный сигнал. Ложные частотные компоненты сигнала (отсутствующие в спектре исходного сигнала) получили название alias (ложная частота, побочная низкочастотная составляющая). Частота ложных компонент зависит от разницы между частотой сигнала и частотой дискретизации. Например, синусоидальный сигнал с частотой 2 кГц, дискретизованный с частотой 1.5 кГц был бы воспроизведён как синусоида с частотой 500 Гц. Эта проблема получила название наложение частот (aliasing).
Для предотвращения наложения спектров сигнал, подаваемый на вход АЦП, должен быть пропущен через фильтр низких частот для подавления спектральных компонент, частота которых превышает половину частоты дискретизации. Этот фильтр получил название anti-aliasing (антиалиасинговый) фильтр, его применение чрезвычайно важно при построении реальных АЦП.
Хотя наложение спектров в большинстве случаев является нежелательным эффектом, его можно использовать во благо. Например, благодаря этому эффекту можно обойтись без преобразования частоты вниз при оцифровке узкополосного высокочастотного сигнала (смотри смеситель). Для этого, однако, входные аналоговые каскады АЦП должны иметь значительно более высокие параметры, чем это требуется для стандартного использования АЦП на основной (видео или низшей) гармонике.
Некоторые характеристики АЦП могут быть улучшены путём использования методики подмешивания псевдослучайного сигнала (англ. dither). Она заключается в добавлении к входному аналоговому сигналу случайного шума (белый шум) небольшой амплитуды. Амплитуда шума, как правило, выбирается на уровне половины МЗР. Эффект от такого добавления заключается в том, что состояние МЗР случайным образом переходит между состояниями 0 и 1 при очень малом входном сигнале (без добавления шума МЗР был бы в состоянии 0 или 1 долговременно). Для сигнала с подмешанным шумом вместо простого округления сигнала до ближайшего разряда происходит случайное округление вверх или вниз, причём среднее время, в течение которого сигнал округлён к тому или иному уровню зависит от того, насколько сигнал близок к этому уровню. Таким образом, оцифрованный сигнал содержит информацию об амплитуде сигнала с разрешающей способностью лучше, чем МЗР, то есть происходит увеличение эффективной разрядности АЦП. Негативной стороной методики является увеличение шума в выходном сигнале. Фактически, ошибка квантования размазывается по нескольким соседним отсчётам. Такой подход является более желательным, чем простое округление до ближайшего дискретного уровня. В результате использования методики подмешивания псевдослучайного сигнала мы имеем более точное воспроизведение сигнала во времени. Малые изменения сигнала могут быть восстановлены из псевдослучайных скачков МЗР путём фильтрации. Кроме того, если шум детерминирован (амплитуда добавляемого шума точно известна в любой момент времени), то его можно вычесть из оцифрованного сигнала, предварительно увеличив его разрядность, тем самым почти полностью избавиться от добавленного шума.
Звуковые сигналы очень малых амплитуд, оцифрованные без псевдослучайного сигнала, воспринимаются на слух очень искажёнными и неприятными. При подмешивании псевдослучайного сигнала истинный уровень сигнала представлен средним значением нескольких последовательных отсчётов.
Однако, в последнее время (2009), в связи с удешевлением 24-битных АЦП, имеющих даже без dihter’а динамический диапазон более 120 дБ, что на несколько порядков превышает полный воспринимаемый человеком диапазон слуха, данная технология потеряла актуальность в звукотехнике. При этом, она используется в ВЧ и СВЧ технике, где битность АЦП обычно мала из-за высокой частоты дискретизации.
Очень похожий процесс, также называемый dither или диффузия ошибок, применяется для представления полутонов изображений в компьютерной графике при малом количестве бит на пиксел. При этом изображение становится зашумленным, но визуально воспринимается реалистичнее чем то же изображение полученное простым квантованием.
Как правило, сигналы оцифровываются с минимально необходимой частотой дискретизации из соображений экономии, при этом шум квантования является белым, то есть его спектральная плотность мощности равномерно распределена во всей полосе. Если же оцифровать сигнал с частотой дискретизации, гораздо большей, чем по теореме Котельникова-Шеннона, а затем подвергнуть цифровой фильтрации для подавления спектра вне частотной полосы исходного сигнала, то отношение сигнал/шум, будет лучше, чем при использовании всей полосы. Таким образом можно достичь эффективного разрешения большего, чем разрядность АЦП.
Передискретизация также может быть использована для смягчения требований к крутизне перехода от полосы пропускания к полосе подавления антиалиасингового фильтра. Для этого сигнал оцифровывают, например, на вдвое большей частоте, затем производят цифровую фильтрацию, подавляя частотные компоненты вне полосы исходного сигнала, и, наконец, понижают частоту дискретизации путём децимации.
Ниже перечислены основные способы построения электронных АЦП:
Неэлектронные АЦП обычно строятся на тех же принципах.
Как правило, выпускаются в виде микросхем.
Для большинства АЦП разрядность составляет от 6 до 24 бит, частота дискретизации до 1 МГц. Мега- и гигагерцовые АЦП также доступны (февраль 2002). Мегагерцовые АЦП требуются в цифровых видеокамерах, устройствах видеозахвата и цифровых TV-тюнерах для оцифровки полного видеосигнала. Коммерческие АЦП обычно имеют выходную ошибку от ±0,5 до ±1,5 МЗР.
Один из факторов увеличивающих стоимость микросхем — это количество выводов, поскольку они вынуждают делать корпус микросхемы больше, и каждый вывод должен быть присоединён к кристаллу. Для уменьшения количества выводов часто АЦП, работающие на низких частотах дискретизации, имеют последовательный интерфейс. Применение АЦП с последовательным интерфейсом зачастую позволяет увеличить плотность монтажа и создать плату с меньшей площадью.
Часто микросхемы АЦП имеют несколько аналоговых входов, подключённых внутри микросхемы к единственному АЦП через аналоговый мультиплексор. Различные модели АЦП могут включать в себя устройства выборки-хранения, инструментальные усилители или высоковольтный дифференциальный вход и другие подобные цепи.
АЦП встроены в большую часть современной звукозаписывающей аппаратуры, поскольку обработка звука делается, как правило, на компьютерах; даже при использовании аналоговой записи АЦП необходим для перевода сигнала в PCM-поток, который будет записан на компакт-диск.
Современные АЦП, используемые в звукозаписи, могут работать на частотах дискретизации до 192 кГц. Многие люди, занятые в этой области, считают, что данный показатель избыточен и используется из чисто маркетинговых соображений (об этом свидетельствует теорема Котельникова-Шеннона). Можно сказать, что звуковой аналоговый сигнал не содержит столько информации, сколько может быть сохранено в цифровом сигнале при такой высокой частоте дискретизации, и зачастую для Hi-Fi (класс аппаратуры) аудиотехники используется частота дискретизации 44.1 кГц (стандартная для CD) или 48 кГц (типична для представления звука в компьютерах). Однако широкая полоса упрощает и удешевляет реализацию антиалиасинговых фильтров, позволяя делать их с меньшим числом звеньев или с меньшей крутизной в полосе заграждения, что положительно сказывается на фазовой характеристике фильтра в полосе пропускания.
Аналого-цифровые преобразователи для звукозаписи имеют широкий диапазон цен — от $100 до $10 000 и выше за двухканальный АЦП.
АЦП для звукозаписи, используемые на ЭВМ, бывают внутренние и внешние. Также существует бесплатный программный комплекс PulseAudio для Linux, позволяющий использовать вспомогательную(-ые) ЭВМ как внешние ЦАП/АЦП для основной ЭВМ с гарантированным временем запаздывания.
Аналого-цифровое преобразование используется везде, где требуется обрабатывать, хранить или передавать сигнал в цифровой форме.
Wikimedia Foundation. 2010.
dic.academic.ru
1 июля
В
В технической документации производители указывают характеристики АЦП по-разному, и это сбивает с толку инженеров. Самые большие споры вызывают два параметра: разрешение и точность. Попробуем разобраться, чем они отличаются, как соотносятся с другими характеристиками, такими как динамический диапазон или порог шума, и как их применять.
Динамический диапазон, точность и разрешение
Динамический диапазон (ДД) есть разница между максимальным и минимальным
сигналами, которые может измерить преобразователь. В качестве максимального
сигнала может быть взят размах, амплитуда или среднеквадратичное
напряжение полной шкалы (ПШ). Эти величины разные. Например, для
синусоидального сигнала с амплитудой 1 В размах составляет 2 В, а
среднеквадратичное напряжение — 0,707 В. В качестве минимально различимого
сигнала обычно берут среднеквадратичное напряжение шума на входе АЦП в
отсутствие сигнала. Это значение зависит от полосы частот, на которой оно
измеряется. При удвоении частоты шум увеличивается в 1,41 раза или на
3 дБ. Важно понимать, что ДД — величина, относящаяся к какой-либо
частотной полосе. Часто ДД и отношение сигнал-шум (SNR) устройства считают
одной и той же величиной и измеряют в дБ:
ДД = SNR = VПШ/Vш = 20 lg (VПШ/Vш).
Иногда производители берут не среднеквадратичное напряжение ПШ, а его
амплитуду или размах, чтобы «увеличить» динамический диапазон на несколько
дБ.
Разрешение и точность — параметры, которые часто путают, когда речь идет о
производительности АЦП. Разрешение — это количество разрядов, используемых при
оцифровке входного сигнала. Например, 16-разрядный АЦП разбивает шкалу на 216
(65536) позиций выходного кода. Минимальный сигнал, который устройство может
измерить, равен 1 разряду (МЗР — младший значащий разряд) или 1/65536 доле
напряжения ПШ.
Точность АЦП характеризует, насколько близко фактический выходной код совпадает
с теоретическим для данного входного аналогового сигнала. Другими словами, это
количество разрядов выходного кода, которые несут полезную информацию о входном
сигнале.
Как уже говорилось, точность АЦП может оказаться намного ниже разрешения из-за
внутренних и внешних источников шума. В этом случае 4 МЗР — это
случайный шум АЦП. Часто ДД преобразователя и его точность — это одно и то же.
На рисунке 1 приведена общая схема АЦП.
Рис. 1. Общая схема АЦП |
Идеальный преобразователь генерирует выходной код как функцию аналогового входного и опорного напряжений:
Выходной код = VПШ [VIN+ – VIN-]/[VREF+ – VREF-] = VПШ VIN/VREF.
Каждый выходной код — это доля опорного напряжения.
Важно заметить, что ДД преобразователя должен соответствовать максимальной
амплитуде преобразуемого сигнала, чтобы точность преобразования была
наиболь-
шей.
Пусть входной сигнал меняется в пределах 0…2,5 В, а VREF = 3,3 В,
как показано на рисунке 2.
Рис. 2. Несогласованный входной сигнал АЦП |
Как мы говорили, 16-разрядный АЦП генерирует 65536 кодовых позиций или
шагов, МЗР = 3,3/65536 = 50,35 мкВ. Для идеального АЦП все коды будут
иметь одинаковую ширину, равную 1 МЗР. Максимальное входное напряжение
составляет 2,5 В, это 49652 выборки. Соответственно, 15884 кода не
используются, поэтому эффективная разрядность (ENOB) или потеря в точности
составят 0,4 разряда.
Потеря в ENOB оказывается тем больше, чем больше разница между максимальным
входным сигналом и VREF. Если максимальный входной сигнал равен,
например, 1,2 В, а VREF = 3,3 В, то ENOB уменьшится
на 1,5 разряда. Именно поэтому важно согласовать динамический диапазон АЦП и
максимальную амплитуду сигнала. Рассмотрим несколько примеров применения этих
параметров.
Для простоты будем считать, что для цифровой камеры ДД — это диапазон от
самого темного до самого яркого света, который можно обнаружить, выраженный в
битах. Минимальная скорость передачи (разрешение) АЦП определяется динамическим
диапазоном (точностью) датчика изображения. Например, если ДД равен 1000:1
(60 дБ), то АЦП должен иметь по крайней мере 10 разрядов (210 =
1024 уровня), чтобы информация не потерялась. На практике лучше сделать запас,
например, использовать 12-разрядный преобразователь, чтобы свести к минимуму
влияние помех.
Утверждать, что камера имеет точность 12 разрядов только потому, что такова
разрядность АЦП бессмысленно, поскольку не приняты во внимание внешний шум и
возможности пиксела.
Из сказанного выше становится ясно, что точность системы совпадает с
разрядностью АЦП только в том случае, если датчик имеет достаточный ДД. Тоновый
и динамический диапазоны системы не могут превышать ДД датчика. Понятия
«12-разрядная камера» и «камера с 12-разрядным АЦП» — не одно и то же.
Резистивный датчик температуры
Обычно датчики этого вида изготавливаются из платины и имеют следующие
характеристики: сопротивление при температуре 0°С = 100 Ом, изменение
сопротивления на 1°С = 0,385 Ом, ток включения 1 мА, температурный диапазон
0…500°С.
Резистивные датчики работают при малом токе порядка 1 мА. При изменении
температуры на 1°С сопротивление изменится на 0,385 Ом, поэтому малейшая
погрешность измерения сопротивления приведет к большой ошибке в измерении
температуры.
Резистивные датчики температуры регистрируют изменение температуры на 0,1°С.
Это значение 1 МЗР в диапазоне 0…500°С. Соответствующее изменение
сопротивления составляет 192,5 Ом. Отсюда напряжение в данном диапазоне будет
равно 192,5 мВ, а ДД = VПШ/МЗР = 192,5 / 38,5 = 5000. Следовательно,
для рассматриваемой системы подойдет 13-разрядный АЦП.
Поскольку напряжение на термометре варьируется в диапазоне 100…292,5 мВ
с очень небольшим МЗР, чтобы его различил АЦП, то следует усилить сигнал. Пусть
усилитель имеет постоянный коэффициент усиления 17. Тогда входное
напряжение будет находиться в пределах 1,7…4,92 В. Как говорилось ранее
(см рис. 2), при таком диапазоне входных напряжений АЦП используется не в
полную силу. Принимая, что напряжение ПШ = 5 В, получаем, что
ENOB = 1,44 ln [VПШ/МЗР] = 1,44 ln[5 В/
38,5 мкВ] ≈ 17 разрядов. Для этой задачи лучше взять хороший
сигма-дельта преобразователь.
Современные счетчики электроэнергии — сложные электронные устройства,
имеющие высокую точность и широкий ДД. ДД счетчика первого класса равен 2000:1,
минимальный входной сигнал составляет примерно 0,5 мВ, напряжение ПШ = 1
В.
Максимальная погрешность счетчика составляет 0,1%. Соответственно, точность
должна быть не хуже 500 нВ — это минимальный допустимый входной
сигнал. Количество выборок 1 В/500 нВ = 2·106. Это
соответствует эффективной разрядности 21. Заметим, что при этом подходит
не любой 21-разрядный АЦП. Необходимо, чтобы он имел очень низкий пороговый шум
и различал столь малое входное напряжение. Еще более строгие требования
предъявляются к току счет-
чика.
Точность АЦП зависит не только от производительности или другого параметра АЦП.
Она определяется и внешними элементами схемы, поскольку ДД преобразователя
определяется схемой устройства.
Вы можете скачать эту статью в формате pdf здесь.
www.russianelectronics.ru
 Аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC). Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее некоторые неэлектронные устройства с цифровым выходом следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.
Аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC). Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее некоторые неэлектронные устройства с цифровым выходом следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП — связано с его разрядностью. В случае единичного измерения без учёта шумов разрешение напрямую определяется разрядностью АЦП.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП измеряется в битах, в троичных АЦП измеряется в тритах. Например, двоичный 8-разрядный АЦП способен выдать 256 дискретных значений (0…255), поскольку 2^8 = 256, троичный 8-разрядный АЦП способен выдать 6561 дискретное значение, поскольку 3^8=6561. Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений. На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (effective number of bits, ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. Для достижения заявленной разрядности отношение сигнал/шум входного сигнала должно быть примерно 6 дБ на каждый бит разрядности (6 дБ соответствует двукратному изменению уровня сигнала).
По способу применяемых алгоритмов АЦП делят на:
Передаточная характеристика АЦП — зависимость числового эквивалента выходного двоичного кода от величины входного аналогового сигнала. Говорят о линейных и нелинейных АЦП. Такое деление условное. Обе передаточные характеристики — ступенчатые. Но для «линейных» АЦП всегда возможно провести такую прямую линию, чтобы все точки передаточной характеристики, соответствующие входным значениям \delta\cdot2^k (где \delta — шаг дискретизации, k лежит в диапазоне 0..N, где N — разрядность АЦП), были от неё равноудалены.
Линейные АЦП Большинство АЦП считаются линейными, хотя аналого-цифровое преобразование, по сути, является нелинейным процессом (поскольку операция отображения непрерывного пространства в дискретное — операция нелинейная). Термин линейный применительно к АЦП означает, что диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением, то есть выходное значение k достигается при диапазоне входных значений от m(k + b) до m(k + 1 + b), где m и b — некоторые константы. Константа b, как правило, имеет значение 0 или −0.5. Если b = 0, АЦП называют квантователь с ненулевой ступенью (mid-rise), если же b = −0,5, то АЦП называют квантователь с нулём в центре шага квантования (mid-tread).
Нелинейные АЦП Если бы плотность вероятности амплитуды входного сигнала имела равномерное распределение, то отношение сигнал/шум (применительно к шуму квантования) было бы максимально возможным. По этой причине обычно перед квантованием по амплитуде сигнал пропускают через безынерционный преобразователь, передаточная функция которого повторяет функцию распределения самого сигнала. Это улучшает достоверность передачи сигнала, так как наиболее важные области амплитуды сигнала квантуются с лучшим разрешением. Соответственно, при цифро-аналоговом преобразовании потребуется обработать сигнал функцией, обратной функции распределения исходного сигнала.
Это тот же принцип, что и используемый в компандерах, применяемых в магнитофонах и различных коммуникационных системах, он направлен на максимизацию энтропии. (Не путать компандер с компрессором!) Например, голосовой сигнал имеет лапласово распределение амплитуды. Это означает, что окрестность нуля по амплитуде несёт больше информации, чем области с большей амплитудой. По этой причине логарифмические АЦП часто применяются в системах передачи голоса для увеличения динамического диапазона передаваемых значений без изменения качества передачи сигнала в области малых амплитуд. 8-битные логарифмические АЦП с a-законом или μ-законом обеспечивают широкий динамический диапазон и имеют высокое разрешение в наиболее критичном диапазоне малых амплитуд; линейный АЦП с подобным качеством передачи должен был бы иметь разрядность около 12 бит.
Точность Имеется несколько источников погрешности АЦП. Ошибки квантования и (считая, что АЦП должен быть линейным) нелинейности присущи любому аналого-цифровому преобразованию. Кроме того, существуют так называемые апертурные ошибки, которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта). Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд (англ.). В приведённом выше примере 8-битного двоичного АЦП ошибка в 1 МЗР составляет 1/256 от полного диапазона сигнала, то есть 0,4 %, в 5-тритном троичном АЦП ошибка в 1 МЗР составляет 1/243 от полного диапазона сигнала, то есть 0,412 %, в 8-тритном троичном АЦП ошибка в 1 МЗР составляет 1/6561, то есть 0,015 %.
Частота дискретизации Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала. Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП. Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации), и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции. Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова — Шеннона точное восстановление возможно, только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала. Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным, по крайней мере, от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения (УВХ). УВХ, как правило, хранит входное напряжение на конденсаторе, который соединён со входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение. Многие АЦП, выполненные в виде интегральных микросхем, содержат встроенное УВХ.
Наложение спектров Все АЦП работают путём выборки входных значений через фиксированные интервалы времени. Следовательно, выходные значения являются неполной картиной того, что подаётся на вход. Глядя на выходные значения, нет никакой возможности установить, как вёл себя входной сигнал между выборками. Если известно, что входной сигнал меняется достаточно медленно относительно частоты дискретизации, то можно предположить, что промежуточные значения между выборками находятся где-то между значениями этих выборок. Если же входной сигнал меняется быстро, то никаких предположений о промежуточных значениях входного сигнала сделать нельзя, а следовательно, невозможно однозначно восстановить форму исходного сигнала. Если последовательность цифровых значений, выдаваемая АЦП, где-либо преобразуется обратно в аналоговую форму цифро-аналоговым преобразователем, желательно, чтобы полученный аналоговый сигнал был максимально точной копией исходного сигнала. Если входной сигнал меняется быстрее, чем делаются его отсчёты, то точное восстановление сигнала невозможно, и на выходе ЦАП будет присутствовать ложный сигнал. Ложные частотные компоненты сигнала (отсутствующие в спектре исходного сигнала) получили название alias (ложная частота, побочная низкочастотная составляющая). Частота ложных компонент зависит от разницы между частотой сигнала и частотой дискретизации. Например, синусоидальный сигнал с частотой 2 кГц, дискретизованный с частотой 1.5 кГц, был бы воспроизведён как синусоида с частотой 500 Гц. Эта проблема получила название наложение частот (aliasing). Для предотвращения наложения спектров сигнал, подаваемый на вход АЦП, должен быть пропущен через фильтр нижних частот для подавления спектральных компонент, частота которых превышает половину частоты дискретизации. Этот фильтр получил название anti-aliasing (антиалиасинговый) фильтр, его применение чрезвычайно важно при построении реальных АЦП. Вообще, применение аналогового входного фильтра интересно не только по этой причине. Казалось бы, цифровой фильтр, который обычно применяется после оцифровки, имеет несравненно лучшие параметры. Но, если в сигнале присутствуют компоненты, значительно более мощные, чем полезный сигнал, и достаточно далеко отстоящие от него по частоте, чтобы быть эффективно подавленными аналоговым фильтром, такое решение позволяет сохранить динамический диапазон АЦП: если помеха на 10 дБ сильнее сигнала, на неё впустую будет тратиться, в среднем, три бита разрядности. Хотя наложение спектров в большинстве случаев является нежелательным эффектом, его можно использовать во благо. Например, благодаря этому эффекту можно обойтись без преобразования частоты вниз при оцифровке узкополосного высокочастотного сигнала (смотри смеситель). Для этого, однако, входные аналоговые каскады АЦП должны иметь значительно более высокие параметры, чем это требуется для стандартного использования АЦП на основной (видео или низшей) гармонике. Также для этого необходимо обеспечить эффективную фильтрацию внеполосных частот до АЦП, так как после оцифровки нет никакой возможности идентифицировать и/или отфильтровать большинство из них.
основные способы построения электронных АЦП:
audioakustika.ru
jparenas, это вопрос, который регулярно возвращается, будучи источником путаницы при работе с АЦП. Она тесно связана с классической путаницей: Full Scale Voltage (FS) в зависимости от источника опорного напряжения (Vref). Для простоты рассмотрим гипотетический 3-разрядный АЦП (\ $ N \ $ = 3), без компенсации на уровне 0,5 LSB на входе (как, я думаю, происходит на ATmega328p) — в этом случае результаты Полученное здесь не сильно отличается. Три части:
(a) См. передаточную функцию (a) на изображении ниже, где Va — аналоговое напряжение, а Vd — преобразованное цифровое значение. FS это просто напряжение, которое соответствует переходу к максимальному цифровому значению (7 или \ $ 2 ^ N-1 \ $). Кроме того, есть семь шагов по горизонтали и семь шагов по вертикали, где каждый шаг происходит кратно 1/7 FS. Пусть FS = 4,375 В, тогда каждый аналоговый шаг равен 0,625 В. Обратите внимание, что наклонная пунктирная линия, соединяющая координаты (0; 000) с (FS; 111), представляет идеальное преобразование, которое захочет каждый инженер. Итак:
$$ Vd = int \ left (\ frac {Va} {FS} \ times 7 \ right) $$
Здесь мы можем выделить Va, чтобы найти простое выражение:
$$ Va = \ frac {Vd} {7} \ times FS $$
Но подожди! Все не так просто: чтобы быть более строгим, мы можем видеть, что напряжение Va фактически может принимать любое значение в пределах интервала. Применение определения \ $ int () \ $ function:
$$ \ frac {Vd} {7} \ times FS \ leq Va < \ frac {(Vd + 1)} {7} \ times FS $$
(b) Теперь посмотрите передаточную функцию, показанную на (b). Обратите внимание, что если бы был еще один дополнительный шаг в 1/7 FS, мы могли бы связать его с полным цифровым значением 8 (или \ $ 2 ^ N \ $). Вуаля! Давайте назовем это Vref:
$$ Vref = \ frac {8} {7} FS $$
Обратите внимание, что для нашего FS = 4,375 V \ $ \ Rightarrow \ $ Vref = 5 V. См. выражение \ $ FS = \ frac {7} {8} Vref \ $. Это еще один способ заявить, что FS остается на 1 LSB ниже Vref. Здесь не имеет значения, но для АЦП с входной компенсацией 0,5 LSB FS будет на 1,5 LSB ниже Vref.
(c) Наконец, перепишите все это, основываясь только на Vref, удалив этот дополнительный шаг. Таким образом, мы получаем передаточную функцию, показанную в (c) — аналогичную той, которая найдена в таблицах, полностью основанную на факторе \ $ 2 ^ N \ $. Все счастливы! Но обратите внимание, что есть 7 шагов по вертикали и 8 шагов по горизонтали. Выражение для Vd заменяется на:
$$ Vd = int \ left (\ frac {Va} {Vref} \ times 8 \ right) $$
также:
$$ \ frac {Vd} {8} \ times Vref \ leq Va < \ frac {(Vd + 1)} {8} \ times Vref $$
Функции передачи АЦП:
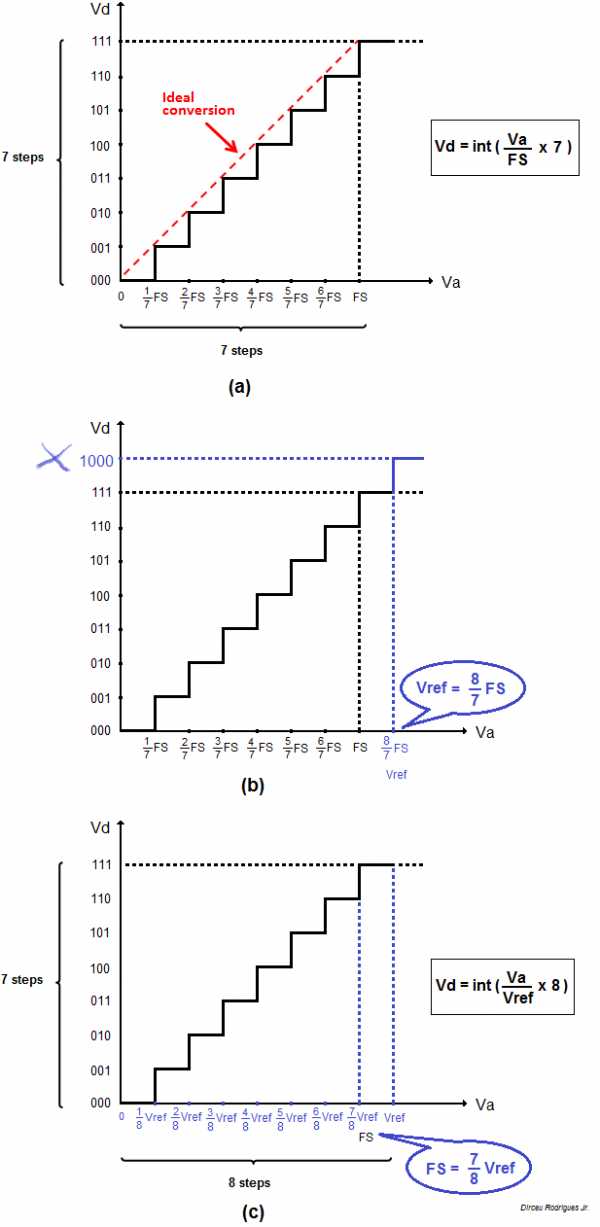
Таким образом, мы можем использовать либо \ $ (2 ^ N-1) \ $, либо \ $ 2 ^ N \ $, поскольку они правильно связаны со значениями FS или Vref соответственно. Согласно сюжету (c), плохие новости заключаются в том, что мы не можем «измерить» значение Vref (действительно, определить, когда происходит переход к этому значению). Конечно, мы можем преодолеть проблему, используя резистивные делители и усилитель. ops на входе АЦП в соответствии с желаемым значением. Но на практике это может не стоить: кроме очень небольших различий (для 10-разрядного АЦП или выше), также существуют неидеальности преобразователя AD. Наконец, используемый допуск резистора может «испортить» все это.
Преимущество использования деления на \ $ 2 ^ N \ $ заключается в том, что в простых микроконтроллерах (особенно 8-битных) нет инструкции по делению: это можно заменить несколькими сдвигами вправо. Разница в том, что округление для знакового деления «в ноль», а для арифметического сдвига вправо — «отрицательная бесконечность». Более сложные процессоры, такие как ARM (кроме Cortex-M0), уже включают в себя инструкции по разделению на несколько циклов и многократные сдвиги за один цикл через собственный цилиндр — с небольшой разницей в производительности.
ubuntugeeks.com
Аналоговый компаратор – электронная схема, принимающая на свои входы два аналоговых сигнала и выдающая логический «0» или «1», в зависимости от того, какой из сигналов больше.
Два входа для подачи аналоговых сигналов носят названия неинвертирующий (+) и инвертирующий (-). Если на неинвертирующем входе напряжение больше, чем на инвертирующем, выходной сигнал равен логической «1», иначе – логическому «0».
Будучи включенным, компаратор позволяет сравнивать значения напряжений, присутствующих на соответствующих входах микроконтроллера.
Результатом сравнения является логическое значение, которое может быть прочитано внутри программы. По результату сравнения может быть сгенерировано прерывание, а также осуществлен захват состояния таймера-счетчика.
Чтобы выводы микроконтроллера, обладающие соответствующей альтернативной функцией, можно было использовать аналоговым компаратором, они должны быть сконфигурированы как аналоговые входы.
Аналого-цифровой преобразователь (АЦП) – это устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал), чаще всего – двоичный. Обратное преобразование осуществляется при помощи цифро-аналогового преобразователя (ЦАП).
В качестве аналогового сигнала может выступать любая физическая непрерывно меняющаяся величина либо ее эквивалент. Чаще всего в качестве входного сигнала используется эквивалентный сигнал напряжения для получения цифровой информации о температуре, токе, влажности и т.д.
Большинство аналого-цифровых преобразователей являются линейными, то есть диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением. Основой построения АЦП является аналоговый компаратор.
Разрешение АЦП – минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП. Обычно измеряется в вольтах.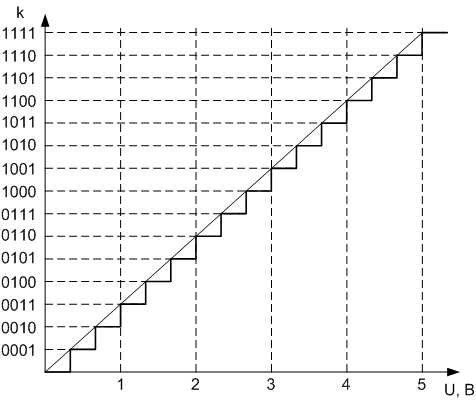
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. Измеряется в битах. Например, АЦП, способный выдать 28=256 дискретных значений (0..255), имеет разрядность 8 бит.
Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений.
где N – разрядность АЦП.
При этом напряжение на входе преобразователя можно оценить, зная полученное цифровое значение аналого-цифрового преобразования Value
На практике разрешение АЦП ограничено отношением сигнал-шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (effective number of bits — ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумленного сигнала младшие биты выходного кода практически бесполезны, так как содержат шум.
Дискретизацией сигнала называется измерительное преобразование непрерывного сигнала x(t) в последовательность мгновенных значений этого сигнала X(kiT), соответствующих определенным моментам времени kiT (T – шаг дискретизации).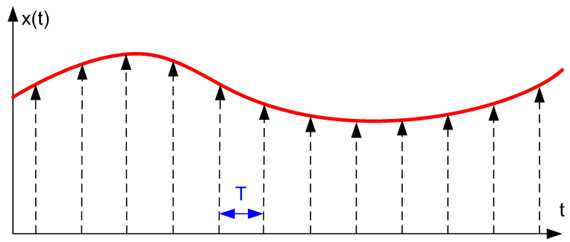
Дискретизацию сигнала по времени можно проводить с постоянным шагом T= const или с переменным шагом T= var.
Частота дискретизации – частота, с которой производится аналого-цифровое преобразование сигнала.
Время преобразования – время от начала преобразования до появления на выходе АЦП соответствующего кода.
Опорное напряжение– напряжение, соответствующее максимальному выходному коду.
Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным, по крайней мере, от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача может решаться путем использования специальной схемы на входе АЦП – устройства выборки-хранения (УВХ). УВХ, как правило, хранит входное напряжение в конденсаторе, который соединен с входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании – хранение. Как правило, модули АЦП содержат встроенное УВХ.
Назад
prog-cpp.ru
Ниже перечислены основные способы построения электронных АЦП:
АЦП прямого преобразования или параллельный АЦП содержит по одному компаратору на каждый дискретный уровень входного сигнала. В любой момент времени только компараторы, соответствующие уровням ниже уровня входного сигнала, выдадут на своём выходе сигнал превышения. Сигналы со всех компараторов поступают на логический шифратор, генерирующий бинарный цифровой код в зависимости от количества логических единиц, присутствующих на его входе. Данные с шифратора фиксируются в параллельном регистре, и, в общем случае, частота дискретизации АЦП может зависеть лишь от аппаратных характеристик логических и аналоговых элементов, а также от частоты требуемой выборки значений. Параллельные АЦП очень быстры, но обычно имеют разрешение не более 8 бит (256 компараторов), так как влекут за собой большие аппаратные затраты. АЦП этого типа имеют очень большой размер кристалла микросхемы, высокую входную емкость, и могут выдавать кратковременные ошибки на выходе. Часто используются для видео или других высокочастотных сигналов, а также широко применяются в промышленности для отслеживания быстро изменяющихся процессов в реальном времени.
Последовательно-параллельные АЦП сохраняя высокое быстродействие позволяет значительно уменьшить количество компараторов, требуещееся для преобразования аналогового сигнала в цифровой. Содержат в своем составе два — три параллельных АЦП. Второй АЦП служит для уменьшения ошибки квантования первого АЦП путем оцифровки этой ошибки. Для увеличения скорости выходного оцифрованного потока данных в последовательно-параллельных АЦП применяется конвейерная работа параллельных АЦП.
АЦП последовательного приближения или АЦП с поразрядным уравновешиванием содержит компаратор, вспомогательный ЦАП и регистр последовательного приближения. АЦП преобразует аналоговый сигнал в цифровой за N шагов, где N — разрядность АЦП. На каждом шаге определяется по одному биту искомого цифрового значения, начиная от СЗР и заканчивая МЗР. Последовательность действий по определению очередного бита заключается в следующем. На вспомогательном ЦАП выставляется аналоговое значение, образованное из битов, уже определённых на предыдущих шагах; бит, который должен быть определён на этом шаге, выставляется в 1, более младшие биты установлены в 0. Полученное на вспомогательном ЦАП значение сравнивается с входным аналоговым значением. Если значение входного сигнала больше значения на вспомогательном ЦАП, то определяемый бит получает значение 1, в противном случае 0. Таким образом, определение итогового цифрового значения напоминает двоичный поиск. АЦП этого типа обладают одновременно высокой скоростью и хорошим разрешением. Однако при отсутствии устройства выборки хранения погрешность будет значительно больше (представьте, что после оцифровки самого большого разряда сигнал начал меняться).
АЦП дифференциального кодирования ( delta—encoded ADC) содержат реверсивный счетчик, код с которого поступает на вспомогательный ЦАП. Входной сигнал и сигнал со вспомогательного ЦАП сравниваются на компараторе. Благодаря отрицательной обратной связи с компаратора на счётчик код на счётчике постоянно меняется так, чтобы сигнал со вспомогательного ЦАП как можно меньше отличался от входного сигнала. По прошествии некоторого времени разница сигналов становится меньше, чем МЗР, при этом код счётчика считывается как выходной цифровой сигнал АЦП. АЦП этого типа имеют очень большой диапазон входного сигнала и высокое разрешение, но время преобразования зависит от входного сигнала, хотя и ограничено сверху. В худшем случае время преобразования равно Tmax=(2q)/fс, где q — разрядность АЦП, fс — частота тактового генератора счётчика. АЦП дифференциального кодирования обычно являются хорошим выбором для оцифровки сигналов реального мира, так как большинство сигналов в физических системах не склонны к скачкообразным изменениям. В некоторых АЦП применяется комбинированный подход: дифференциальное кодирование и последовательное приближение; это особенно хорошо работает в случаях, когда известно, что высокочастотные компоненты в сигнале относительно невелики.
АЦП сравнения с пилообразным сигналом (некоторые АЦП этого типа называют Интегрирующие АЦП) содержат генератор пилообразного напряжения, компаратор и счётчик времени. Пилообразный сигнал линейно нарастает до некоторого уровня, затем быстро спадает до нуля. В момент начала нарастания запускается счётчик времени. Когда пилообразный сигнал достигает уровня входного сигнала, компаратор срабатывает и останавливает счётчик; значение считывается со счётчика и подаётся на выход АЦП. Данный тип АЦП является наиболее простым по структуре и содержит минимальное число элементов. Вместе с тем простейшие АЦП этого типа обладают довольно низкой точностью и чувствительны к температуре и другим внешним параметрам. Для увеличения точности генератор пилообразного сигнала может быть построен на основе счётчика и вспомогательного ЦАП, однако такая структура не имеет никаких преимуществ по сравнению с АЦП последовательного приближения и АЦП дифференциального кодирования.
АЦП с уравновешиванием заряда (к ним относятся АЦП с двухстадийным интегрированием, АЦП с многостадийным интегрированием и некоторые другие) содержатгенератор стабильного тока, компаратор, интегратор тока, тактовый генератор и счётчик импульсов. Преобразование происходит в два этапа (двухстадийное интегрирование). На первом этапе значение входного напряжения преобразуется в ток (пропорциональный входному напряжению), который подаётся на интегратор тока, заряд которого изначально равен нулю. Этот процесс длится в течение времени TN, где T — период тактового генератора, N — константа (большое целое число, определяет время накопления заряда). По прошествии этого времени вход интегратора отключается от входа АЦП и подключается к генератору стабильного тока. Полярность генератора такова, что он уменьшает заряд, накопленный в интеграторе. Процесс разряда длится до тех пор, пока заряд в интеграторе не уменьшится до нуля. Время разряда измеряется путём счёта тактовых импульсов от момента начала разряда до достижения нулевого заряда на интеграторе. Посчитанное количество тактовых импульсов и будет выходным кодом АЦП. Можно показать, что количество импульсов n, посчитанное за время разряда, равно: n=UвхN(RI0)−1, где Uвх — входное напряжение АЦП, N — число импульсов этапа накопления (определено выше), R — сопротивление резистора, преобразующего входное напряжение в ток, I0 — значение тока от генератора стабильного тока, разряжающего интегратор на втором этапе. Таким образом, потенциально нестабильные параметры системы (прежде всего, ёмкость конденсатора интегратора) не входят в итоговое выражение. Это является следствием двухстадийности процесса: погрешности, введённые на первом и втором этапах, взаимно вычитаются. Не предъявляются жёсткие требования даже к долговременной стабильности тактового генератора и напряжению смещения компаратора: эти параметры должны быть стабильны лишь кратковременно, то есть в течение каждого преобразования (не более 2TN). Фактически, принцип двухстадийного интегрирования позволяет напрямую преобразовывать отношение двух аналоговых величин (входного и образцового тока) в отношение числовых кодов (n и N в терминах, определённых выше) практически без внесения дополнительных ошибок. Типичная разрядность АЦП этого типа составляет от 10 до 18 двоичных разрядов. Дополнительным достоинством является возможность построения преобразователей, нечувствительных к периодическим помехам (например, помеха от сетевого питания) благодаря точному интегрированию входного сигнала за фиксированный временной интервал. Недостатком данного типа АЦП является низкая скорость преобразования. АЦП с уравновешиванием заряда используются в измерительных приборах высокой точности.
Конвейерные АЦП используют два или более шага-поддиапазона. На первом шаге производится грубое преобразование (с низким разрешением). Далее определяется разница между входным сигналом и аналоговым сигналом, соответствующим результату грубого преобразования (со вспомогательного ЦАП, на который подаётся грубый код). На втором шаге найденная разница подвергается преобразованию, и полученный код объединяется с грубым кодом для получения полного выгодного цифрового значения. АЦП этого типа быстры, имеют высокое разрешение и небольшой размер корпуса.
АЦП с промежуточным преобразованием в частоту следования импульсов. Сигнал с датчика проходит через преобразователь уровня, а затем через преобразователь напряжение-частота. Таким образом на вход непосредственно логической схемы поступает сигнал, характеристикой которого является лишь частота импульсов. Логический счётчик принимает эти импульсы на вход в течение времени выборки, таким образом, выдавая к её окончанию кодовую комбинацию, численно равную количеству импульсов, пришедших на преобразователь за время выборки. Такие АЦП довольно медленны и не очень точны, но тем не менее очень просты в исполнении и поэтому имеют низкую стоимость.
Сигма-дельта АЦП (называемые также дельта-сигма АЦП) производит аналого-цифровое преобразование с частотой дискретизации, во много раз превышающей требуемую и путём фильтрации оставляет в сигнале только нужную спектральную полосу.
Неэлектронные АЦП обычно строятся на тех же принципах.
studfiles.net