8-900-374-94-44
Когда я учился программировать, меня всегда раздражало решать на практиках неинтересные задачи. Теперь я преподаю, и мне не хочется, чтобы студенты скучали на моих занятиях.
В этой статье я решаю на языке MIT Scheme задачу шифрования и дешифрования методом RSA [1]. По ряду причин, которые рассматриваются в статье, реализация не может использоваться для криптографической защиты информации.
RSA относится к ассиметричным алгоритмам шифрования: если для шифрования используется открытый ключ, то для дешифрования используется закрытый, и наоборот. Первое свойство позволяет кому угодно зашифровать сообщение открытым ключом в адрес владельца закрытого ключа и тем самым обеспечить его конфиденциальность. Второе свойство позволяет владельцу ключа зашифровать хэш сообщения закрытым ключом, чтобы кто угодно мог дешифровать зашифрованный хэш, сравнить его с хэшем сообщения и определить, было ли сообщение модифицровано.
Первый этап генерации ключей — случайный выбор двух достаточно больших простых чисел p и q. Натуральное число x называется простым, если у него есть ровно два различных делителя: 1 и x. Все другие делители числа располагаются на отрезке от 2 до квадратного корня из x, однако достаточно проверять на кратность только простые делители, принадлежащие этому отрезку.
(define (Primes n)
(define (prime? n primes)
(define (iter divisors)
(or (null? divisors)
(let ([divisor (car divisors)])
(or (> (* divisor divisor) n)
(and (< 0 (remainder n (car divisors))) (iter (cdr divisors))))))
)
(iter primes)
)
(define (iter primes i candidate)
(cond
((= i n) primes)
((prime? candidate (reverse primes)) (iter (cons candidate primes) (+ i 1) (+ candidate 1)))
(else (iter primes i (+ candidate 1)))
)
)
(iter '() 0 2)
)
(define primes (Primes 100))
(define p (car primes))
(define q (car (drop 10 primes))) Произведение найденных простых чисел является первым элементом открытого и закрытого ключей.
Приведённый алгоритм позволяет найти за разумное время только первые миллион простых чисел. В реализациях RSA, используемых для защиты информации, используются алгоритмы поиска простых чисел, позволяющие найти простые числа с большим числом разрядов; благодаря тому, что лучший известный алгоритм разложения числа на простые множители работает за время, пропорциональное экспоненте от количества разрядов, считается что восстановить пару простых чисел по рассматриваемому элементу открытого ключа невозможно [2].
(define n (* p q))
Для вычисления вторых элементов открытого и закрытого ключей используется величина fi, равная функции Эйлера [3], вычисленной на n. Функция Эйлера от x равна количеству натуральных чисел, не больших x и взаимно простых с ним. Для n это количество будет равно произведению p-1 и q-1.
(define fi (* (- p 1) (- q 1)))
Вторым элементом открытого ключа выбирается случайное число e в диапазоне от 1 до fi, являющееся взаимно простым с fi.
то есть таким, что наибольшим общим делителем чисел является 1.
(define (CoprimesLess n)
(define (iter accumulator candidate)
(cond
((= 1 candidate) accumulator)
((= 1 (gcd n candidate)) (iter (cons candidate accumulator) (- candidate 1)))
(else (iter accumulator (- candidate 1)))
)
)
(iter '() (- n 1))
)
(define e (car (drop 5 (CoprimesLess fi))))Для поиска наибольшего общего делителя можно использовать алгоритм Евклида [4].
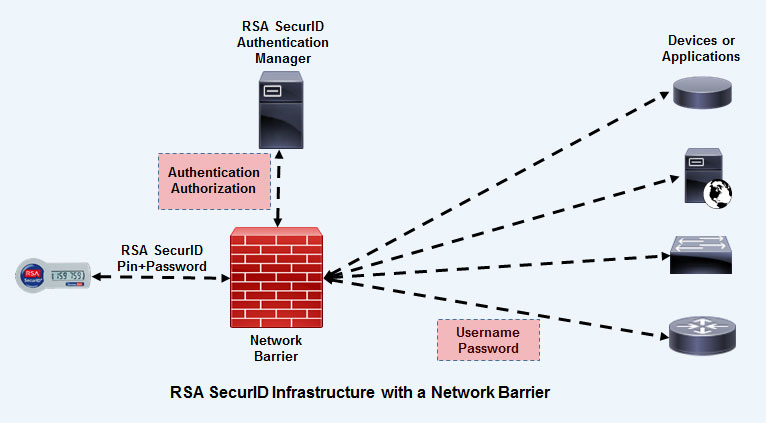
Одним из объектов, изучаемых теорией чисел, является кольцо вычетов [5]. Кольцо вычетов по модулю k — это целые числа от 0 до k-1 и операции сложения и умножения на нём. Сложение в кольце вычетов (a + b mod k) отличается от сложения в группе целых чисел тем, что если результат сложения становится больше k, из него вычитается k, в результате чего этот результат снова оказывается в кольце. Интуитивно, кольцо получается из отрезка соединением его концов.
Как и в группе целых чисел, умножение в кольце вычетов можно задать при помощи сложения, а возведение в степень — при помощи умножения.
Как и в группе целых чисел, получившиеся операции сложения и умножения будут обладать ассоциативностью, то есть:
a + (b + c mod k) mod k = (a + b mod k) + c mod k
a * (b * c mod k) mod k = (a * b mod k) * c mod k
Вторым элементом открытого ключа должно быть число d такое, что его произведение с e в кольце вычетов по модулю n является 1, то есть мультипликативно обратный элемент. Привожу алгоритм поиска такого элемента при помощи расширенного алгоритма Евклида [6].
(define (MultInverseModN a n)
(define (iter a-prev a r-prev r)
(if (>= 1 r) a (let* ([r-next (remainder r-prev r)]
[q (quotient r-prev r)]
[a-next (- a-prev (* q a))])
(iter a a-next r r-next)))
)
(let ([result (iter 0 1 n a)]) (if (< 0 result) result (+ n result)))
)
(define d (MultInverseModN e fi))
При помощи алгоритма RSA можно шифровать сообщения, представленные серией чисел M в диапазоне от 0 до n-1.
Шифрование состоит в возведении M в степень e в кольце вычетов по модулю n, дешифрование — в степень d. Благодаря тому, что умножение является ассоциативным, мы можем возводить в степень x за log(x) операций [7].
(define (PowerModN a b n)
(define (iter accumulator multiplicator power)
(if
(= power 0)
accumulator
(let
((new_accumulator (if (even? power) accumulator (remainder (* accumulator multiplicator) n))))
(iter new_accumulator (* multiplicator multiplicator) (quotient power 2))
)
)
)
(iter 1 a b)
)В моём примере открытый ключ представляет собой пару (250483 31), закрытый — пару (250483 32191). Зашифрованное сообщение 123456 равно 133240.
wikipedia.org/wiki/Modular_arithmetic☰ Оглавление
__del__ и сборка мусора
настройкаВокруг алгоритмов шифрования с отрытым и закрытым ключом
существует множество недопониманий и мистификаций.
Здесь я хотел бы предельно коротко и наглядно, с конкретными
числами и минимумом формул, показать, как это работает.
Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.
Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим.
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
p=3 и q=7.p и q: n=p×q=3×7=21.φ=(p-1)×(q-1)=2×6=12.e, отвечающее следующим критериям:
(i) оно должно быть простое,
(ii) оно должно быть меньше φ — остаются варианты: 3, 5, 7, 11,
(iii) оно должно быть взаимно простое с φ; остаются варианты 5, 7, 11.
Выберем e=5. Это, так называемая, открытая экспонента.Теперь пара чисел {e, n} — это мой открытый ключ. Я отправляю его
вам, чтобы вы зашифровали своё сообщение. Но для меня это ещё не всё.
Я должен получить закрытый ключ.
Мне нужно вычислить число d, обратное е по модулю φ. То есть
остаток от деления по модулю φ произведения d×e должен быть
равен 1. Запишем это в обозначениях, принятых во многих языках
программирования: (d×е)%φ=1. Или (d×5)%12=1. d может быть
равно 5 ((5×5)%12=25%12=1), но чтобы оно не путалось с e в дальнейшем повествовании,
давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 (17×5-12×7=1). Итак d=17.
Пара {d, n} — это секретный ключ, его я оставляю у себя. Его
нельзя сообщать никому. Только обладатель секретного
ключа может расшифровать то, что было зашифровано открытым ключом.
Теперь пришла ваша очередь шифровать ваше сообщение.
Допустим, ваше сообщение это число 19. Обозначим его P=19. Кроме него у вас уже есть мой открытый ключ: {e, n} = {5, 21}. Шифрование выполняется по следующему
алгоритму:
e по модулю n.
То есть, вычисляете 19 в степени 5 (2476099) и берёте
остаток от деления на 21. Получается 10 — это ваши закодированные данные.Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Полученные данные E=10, вы отправляете мне.
Здесь надо заметить, что сообщение P=19 не должно быть больше n=21. иначе ничего не получится.
Я получил ваши данные (E=10), и у меня имеется закрытый ключ {d, n} = {17, 21}.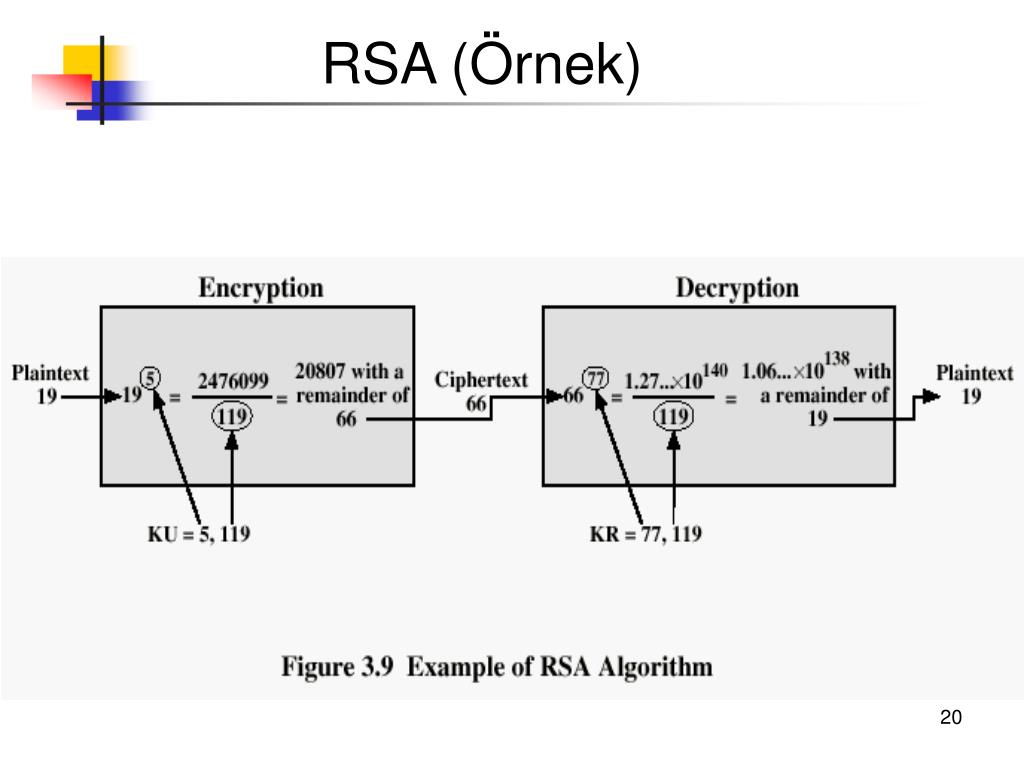
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Начинаем раскодировать:
e использую d.
Возвожу E в степень d: получаю 10 в степени 17 (позвольте, я не
буду писать единичку с семнадцатью нулями). Вычисляю остаток от деления
на 21 и получаю 19 — ваше сообщение.Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение
(E=10), так как ни у кого нет закрытого ключа.
Надёжность шифрования обеспечивается тем, что третьему лицу
(старающемуся взломать шифр) очень трудно вычислить закрытый ключ
по открытому. Оба ключа вычисляются из одной пары простых чисел
(p и q). То есть ключи связаны между собой. Но установить эту
связь очень сложно.
Основной загвоздкой является декомпозиция
модуля n на простые сомножители p и q. Если число является
произведением двух очень больших простых чисел, то его очень трудно разложить
на множители.
Постараюсь это показать на примере. Давайте разложим на множители число 360:
Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмём число 361. Тут нам придётся помучиться.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваш шифр за обозримое время.
Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнёмся от пары простых чисел {p, q} = {17, 19}.
Пусть наш открытый ключ будет {e, n} = {5, 323}, а
закрытый {d, n} = {173, 323}.
Мы готовы к шифрованию. Переведём наше слово в цифровое
представление. Мы можем взять просто номера букв в алфавите.
У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым
ключом {e, n} = {5, 323} и получить
шифровку 197, 272, 2, 304. Эти числа можно передать
получателю, обладающему закрытым ключом {d, n} = {173, 323} и он всё расшифрует.
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придётся отгадывать
ваши секретные ключи.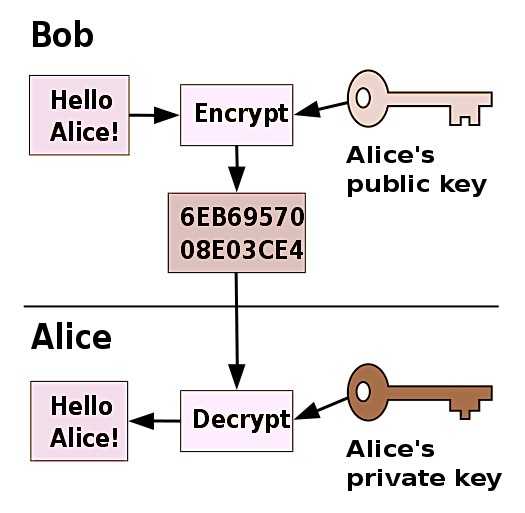
Он взломает ваше сообщение,
не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Упрощённо, это выглядит так. Перед шифрованием, мы применяем
к сообщению правило: b := (b + a) % n. Где a — предыдущая
часть сообщения, а b — следующая. То есть наше сообщение
(11, 17, 15, 19) изменяется. 11 остаётся без изменений.
17 превращается в (11 + 17) % 323 = 28. 15 становится (15 + 28) % 323 = 43. A 19 превращается в 62.
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
Тот, кто получит ваше сообщение, должен будет
проделать обратную операцию, со знаком «минус»: b := (b - a) % n. И только тогда он получит коды
букв.
На практике, в исходное сообщение специально
добавляются случайные и бессмысленные буквы в
начало.
Чтобы даже по первому коду было невозможно
ничего понять. Получатель просто отбрасывает
начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.
Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).
Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось.
Взлом кода RSA — самый важный код в мире?
Код RSA является основой для передачи всех важных данных.
Зашифрованные данные, которые необходимо передавать между двумя сторонами, такие как банковские данные или безопасная связь, основаны на методах кода RSA. Код RSA был изобретен в 1978 году тремя математиками (Ривестом, Шамиром и Адлеманом). Криптография опирается на многочисленные математические методы из теории чисел, которые до XIX в.50-е годы считались в основном теоретическими занятиями с небольшим количеством практических приложений. Сегодня код RSA абсолютно необходим для обеспечения безопасности цифровых коммуникаций.
Чтобы закодировать сообщение с помощью кода RSA, выполните следующие действия:
1) Выберите 2 простых числа p и q (допустим, p=7 и q=5)
2) Перемножьте эти 2 числа (5 ×7 = 35). Это открытый ключ (m), который вы можете сообщить всем. Итак, m = 35.
3) Теперь нам нужно использовать ключ шифрования (e). Предположим, что e = 5. e также обнародовано. (Существуют ограничения на то, какие значения может принимать e — на самом деле e должно быть взаимно простым с (p-1)(q-1))
4) Теперь мы готовы что-то закодировать.
Сначала мы можем присвоить 00 = A, 01 = B, 02 = C, 03 = D, 04 = E и т. д. вплоть до 25 = Z. Итак, слово CODE преобразуется в: 02, 14, 03, 04.
5) Теперь воспользуемся формулой: C = y e (mod m), где y — буква, которую мы хотим закодировать. Итак, для букв CODE получаем: C = 02 5 = 32 (mod 35). C = 14 5 = 537824, что эквивалентно 14 (mod 35). С = 03 5 = 33 (мод. 35). C = 04 5 = 1024, что эквивалентно 09(мод 35). (Mod 35 просто означает, что мы смотрим на остаток при делении на 35). Воспользуйтесь онлайн-калькулятором модуля! Таким образом, наше закодированное слово становится следующим: 32 14 33 09.
Эта форма шифрования с открытым ключом формирует основу Интернета и цифровой передачи информации. Он такой мощный, потому что компьютеры очень быстро и легко его декодируют, если им известны исходные используемые простые числа, и исключительно трудно взломать, если вы попытаетесь угадать простые числа. Из-за ценности использования очень больших простых чисел за их нахождение предлагается большое финансовое вознаграждение.
В настоящее время самое большое простое число в мире состоит из более чем 17 миллионов цифр и было найдено в феврале 2013 года. Любой, кто сможет найти простое число из 100 миллионов цифр, выиграет 100 000 долларов.
Чтобы расшифровать сообщение 11 49 41 нам нужно сделать следующее:
1) В шифровании RSA нам даны и m и e. Это открытые ключи. Например, нам известно, что m = 55 и e = 27. Нам нужно найти два простых числа, которые при умножении дают 55. Это p = 5 и q = 11.
2) Вычислить (p-1)(q -1). В данном случае это (5-1)(11-1) = 40. Назовите это число тета.
3) Вычислите значение d, такое что de = 1 (mod theta). Мы уже знаем, что e равно 27. Поэтому мы хотим, чтобы 27d = 1 (mod 40). Когда d = 3, мы имеем 27 × 3 = 81, что равно 1 (mod 40). Итак, d = 3,9.d (mod m), где C — кодовое слово. Таким образом, для зашифрованного текста 11 49 41: y = 11 3 = 11 (mod 55). у = 49 3 = 04 (mod 55). у = 41 3 = 6 (mod 55).
5) Затем мы преобразуем эти числа обратно в буквы, используя A = 00, B = 01 и т. д. Это дает декодированное слово как: LEG.
Если вам понравился этот пост, вам также могут понравиться:
Как распределяются простые числа? Гипотеза о простых числах-близнецах. Обсуждение изучения простых чисел.
Взлом ISBN и кодов кредитных карт. Математика кодов ISBN и кодов кредитных карт
Важные ресурсы для студентов IB:
1) Руководства по исследованию и ресурсы Paper 3
Я собрал четыре подробных руководства в формате pdf, чтобы помочь студентам подготовиться к исследовательской курсовой работе и исследованиям Paper 3. Руководители по исследованию рассказывают о критериях выставления оценок, распространенных ошибках учащихся, отличных идеях для исследований, технических советах, методах моделирования и различных статистических методах с подробными объяснениями. Я также составил 17 полных вопросов для исследования, которые также являются отличной отправной точкой для исследований.
Руководства по исследованию можно скачать здесь, а вопросы Paper 3 — здесь.
Нравится Загрузка…
Шифрование данных является важной практикой, используемой для защиты передачи данных в Интернете. Это помогает предотвратить несанкционированный доступ к данным, отправленным в Интернете.
Одним из основных алгоритмов, используемых для защиты данных в Интернете, является Rivest, Shamir и Adleman (алгоритм RSA), названный в честь изобретателей этого алгоритма шифрования и дешифрования.
RSA — это алгоритм с открытым ключом, широко используемый для безопасной передачи данных. Это один из основных методов кибербезопасности для защиты данных.
В этом уроке мы обсудим работу алгоритма RSA и то, как этот алгоритм можно реализовать в Python.
Чтобы следовать этому руководству, вам необходимо иметь:
В этом руководстве я буду использовать Visual Studio Code.
Каждая пара алгоритма RSA имеет два ключа, то есть открытый ключ и закрытый ключ. Один ключ используется для шифрования сообщения, которое может быть расшифровано только другим ключом.
Например, предположим, что у нас есть два одноранговых узла, которые общаются друг с другом по каналу, защищенному алгоритмом RSA. Отправитель зашифрует открытый текст открытым ключом получателя. Это делается для того, чтобы получатель был единственным, кто может расшифровать сообщение, используя свой закрытый ключ.
Открытый ключ будет доступен в хранилище открытых ключей. Однако для закрытого ключа, как следует из названия, он хранится в секрете на стороне получателя.
В этом уроке мы будем использовать пакет rsa python .
Откройте свой терминал и используйте команду ниже, чтобы установить его:
pip install rsa
После загрузки пакета первое, что нам нужно сделать, это импортировать rsa в нашу программу:
import rsa
Мы начнем с реализации двух вспомогательных методов для создания закрытого и открытого ключей. Ключи будут представлять собой кортеж открытых и закрытых ключей, а затем записывать ключи в файлы.
Чтобы записать ключи в файлы, мы создадим папку с именем Keys в папке нашего проекта. В папке Keys будет два файла для хранения закрытых и открытых ключей; один ключ в каждом файле.
Мы реализуем это, используя следующий код:
def generateKeys():
(общедоступный ключ, закрытый ключ) = rsa.newkeys (1024)
с open('keys/publcKey.pem', 'wb') как p:
p.write(publicKey.save_pkcs1('PEM'))
с open('keys/privateKey.pem', 'wb') как p:
p.
write(privateKey.save_pkcs1('PEM'))
Теперь, когда мы сохранили ключи в наших файлах, нам нужно загрузить их.
Чтобы загрузить ключи, мы будем использовать приведенный ниже фрагмент кода, который открывает файлы, которые мы создали выше, и возвращает как закрытый, так и открытый ключи:
write(privateKey.save_pkcs1('PEM'))
def loadKeys():
с open('keys/publicKey.pem', 'rb') как p:
publicKey = rsa.PublicKey.load_pkcs1(p.read())
с open('keys/privateKey.pem', 'rb') как p:
privateKey = rsa.PrivateKey.load_pkcs1(p.read())
вернуть приватный ключ, публичный ключ
Затем создайте два других метода для шифрования и расшифровки нашего сообщения.
Начните с создания метода шифрования с помощью приведенного ниже кода. Метод шифрования возьмет сообщение и ключ шифрования.
После определения метода шифрования нам нужно вернуть зашифрованное сообщение. Мы закодируем сообщение в ASCII и дадим ему ключ:
def encrypt(message, key):
вернуть rsa. encrypt (message.encode ('ascii'), ключ)
Теперь создадим метод расшифровки. Этот метод возьмет зашифрованный текст и ключ для расшифровки. Что мы сделаем, так это попытаемся расшифровать сообщение и вернуть расшифрованное сообщение.
Поскольку мы использовали кодировку ASCII , мы также будем использовать декодирование ASCII .
Если это не удается, это означает, что ключ не смог расшифровать сообщение, поэтому мы вернем false. Мы будем использовать приведенный ниже код для реализации метода расшифровки.
encrypt (message.encode ('ascii'), ключ)
def расшифровать (зашифрованный текст, ключ):
пытаться:
вернуть rsa.decrypt (зашифрованный текст, ключ). decode ('ascii')
кроме:
вернуть ложь
Наконец, мы создадим два метода для подписи и проверки нашего сообщения с помощью ключа с помощью хэш-функция sha1 . Этот метод возьмет сообщение и ключ, чтобы мы подписали наше сообщение ключом.
Сообщение, которое мы будем кодировать, получит ключ и наш алгоритм хеширования.
В данном случае SHA-1 .
Метод знака реализуется с помощью кода ниже:
def sign(сообщение, ключ):
вернуть rsa.sign(message.encode('ascii'), ключ, 'SHA-1')
Для проверки сообщения мы создадим метод проверки и передадим сообщение, подпись для проверки и ключ. Итак, что нам нужно сделать, так это попытаться проверить наше сообщение.
Этот метод проверки возвращает алгоритм хеширования, использованный в подписи. Итак, что мы делаем, так это проверяем, что это равно алгоритму хэширования, т.е. ША-1 .
Если подпись подлинная, возвращается значение true. В случае исключения он вернет false, что означает, что проверка не удалась. Это означает, что либо сообщение, либо подпись были изменены и не являются подлинными.
проверка по умолчанию (сообщение, подпись, ключ):
пытаться:
вернуть rsa.verify(message.encode('ascii'), подпись, ключ,) == 'SHA-1'
кроме:
вернуть ложь
Теперь, когда у нас есть алгоритм RSA, мы создадим нашу программу.
Мы начнем с генерации наших ключей.
Мы вызовем метод генерации ключей, загрузим открытый и закрытый ключи, как это реализовано в коде ниже:
generateKeys() открытый ключ, закрытый ключ = load_keys ()
Затем мы возьмем ввод сообщения от пользователя и зашифруем сообщение с помощью открытого ключа. Это представляет отправителя сообщения:
message = input('Напишите свое сообщение здесь:')
зашифрованный текст = зашифровать (сообщение, открытый ключ)
Теперь, когда у нас есть зашифрованный текст, мы сгенерируем подписи, используя приведенный ниже код, чтобы подписать сообщение нашим закрытым ключом. Это позволяет отправителю проверить сообщение с помощью открытого ключа и определить подлинность сообщения:
подпись = знак(сообщение, закрытый ключ)
Далее мы расшифруем наше зашифрованное сообщение, чтобы получить обычный текст. Чтобы реализовать это, мы создадим метод расшифровки и передадим его в зашифрованный текст и закрытый ключ, как показано ниже:
текст = расшифровать (зашифрованный текст, закрытый ключ)
После получения открытого текста следующее, что нужно сделать, это распечатать зашифрованный текст и подпись.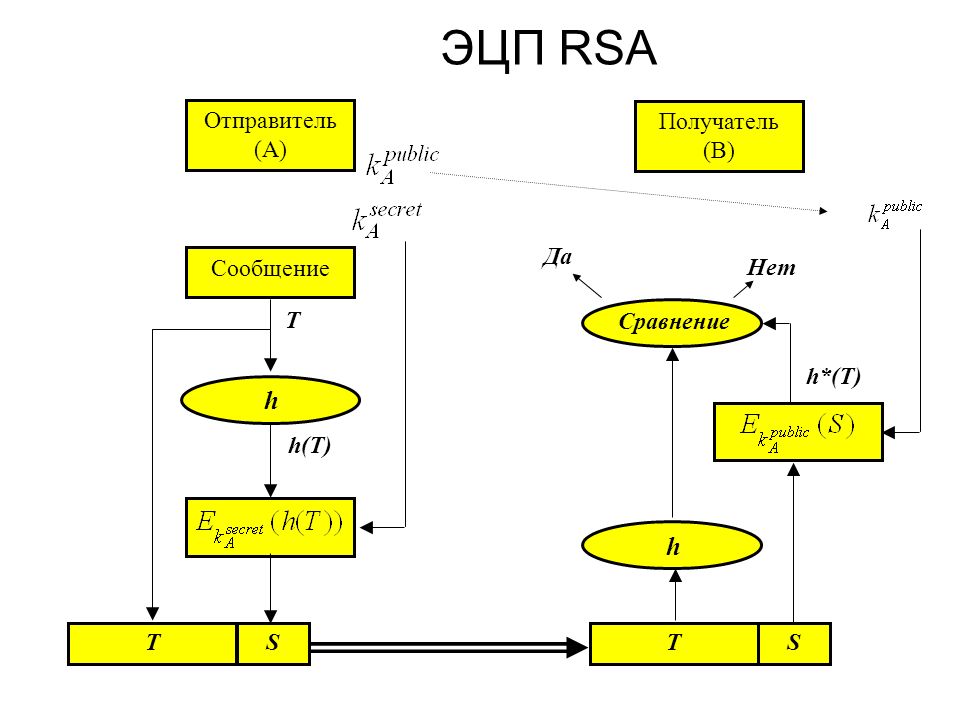
print(f'Зашифрованный текст: {зашифрованный текст}')
печать (f'Подпись: {подпись}')
Мы проверим обычный текст на следующем шаге. Если это обычный текст, то мы указываем, что сообщение было успешно расшифровано иначе не удалось расшифровать сообщение :
если текст:
print(f'Текст сообщения: {текст}')
еще:
print(f'Невозможно расшифровать сообщение.')
Мы проверяем нашу подпись, используя код ниже:
если проверить (текст, подпись, открытый ключ):
print(Подпись успешно проверена)
еще:
print('Не удалось проверить подпись сообщения')
При этом вы можете ввести свое сообщение, зашифровать, а затем расшифровать его.
В этом руководстве мы зашифровали сообщение с помощью открытого ключа и подписали его с помощью нашего закрытого ключа.
Если у вас есть два пира; т. е. узел A разговаривает с узлом B. Когда узел A отправляет сообщение узлу B, сообщение должно быть зашифровано с использованием открытого ключа узла B.