8-900-374-94-44
10 октября 2022
Квадратурный демодулятор, или I/Q demodulator, находит применение в SDR приемниках и трансиверах, а также в приемниках прямого преобразования с аналоговым подавлением зеркального канала, как сделано в QCX. Давайте же разберемся, что это за демодулятор такой, и рассмотрим одну из возможных его реализаций.
Вот структурная схема квадратурного демодулятора:
ВЧ сигнал попадает на делитель, после чего идет на пару смесителей. Сигнал гетеродина (LO), поступающий на смесители, имеет одинаковую частоту и отличается только фазовым сдвигом. Выход I(t) называют синфазным сигналом, или in-phase, а Q(t) — квадратурным сигналом, или quadrature. В чем состоит практическая польза такой схемы, будет показано далее.
Если изменить направление сигналов (вход справа, выход слева), получим квадратурный модулятор, или I/Q modulator. Иногда встречается термин квадратурный смеситель, или I/Q mixer, когда не уточняется, используется ли схема в роли модулятора или демодулятора.
Модуляцию в рамках этой статьи мы рассматривать не будем. По этой теме могу порекомендовать видео IQ Modulator Basics: Operation, Measurements, Impairments, снятое Alan Wolke, W2AEW. Помимо прочего, из видео вы узнаете, как получить BPSK и QPSK сигналы.
На практике квадратурный демодулятор часто реализуют на основе шинных переключателей 74HC4053, FST3253 и подобных. Одна из возможных схем выглядит так (файл PDF):
Трансформатор T1 здесь выступает в роли простого делителя. Выходы X и Y переключаются между землей и сигналом ВЧ (RF). Это эквивалентно умножению на 0 и 1, или меандр, частота которого задается гетеродином (LO). Дальше сигнал проходит через диплексеры и RC-фильтры.
Как результат, на выходах IF_I и IF_Q остается только НЧ сигнал:
В роли гетеродина был использован самодельный генератор сигналов на Si5351. Он позволяет генерировать сигналы с фазовым сдвигом 90°. Частота гетеродина фиксированная — 7.100 МГц.
На первой осциллограмме принимается сигнал с частотой 7.
101 МГц, а на второй осциллограмме — 7.099 МГц. Обратите внимание на фазы синфазного (желтый) и квадратурного (синий) сигналов. В первом случае синфазный сигнал опережает квадратурный на 90°, а во втором — отстает на 90°. Другими словами, по паре сигналов I и Q мы можем определить, находится ли принимаемый сигнал выше частоты гетеродина или ниже.
Важно! В этом заключается принципиальное отличие от приемника прямого преобразования. Обычный ППП не может определить, принимает ли он сигнал выше или ниже частоты гетеродина. Поэтому устранить прием зеркального канала не представляется возможным.
Оказывается, что этой информации достаточно, например, чтобы подавить верхнюю боковую полосу и принять только нижнюю. В SDR-приемниках это осуществляется при помощи цифровой обработки сигналов (DSP). В трансивере QCX качественно та же математика реализована «в железе» на операционных усилителях. Помимо CW и SSB могут быть приняты и более сложные сигналы, например, ЧМ или QAM.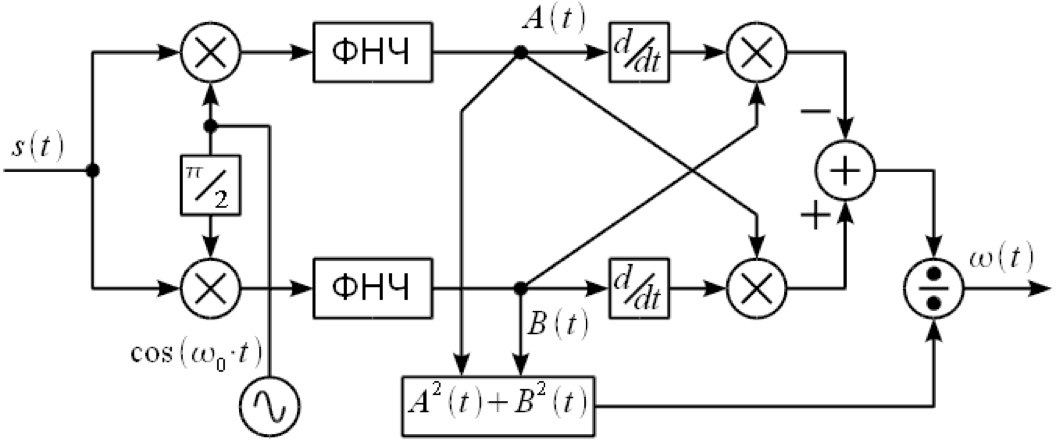
Конкретные схемы и алгоритмы заслуживают отдельных постов.
Приведенный демодулятор имеет некоторые недостатки, ну или особенности, это уже как посмотреть. Во-первых, входной импеданс на порту RF составляет 125-150 Ом на КВ, в зависимости от частоты. Если стоит задача получить ~50 Ом, придется подобрать другое число витков на первичной обмотке T1. Во-вторых, выходы IF_I и IF_Q не тянут низкоомную нагрузку. В-третьих, имеются вносимые потери. При подаче 1 Vpp (High-Z) на порт RF на портах IF_I и IF_Q получаем по 0.25 Vpp.
Из хорошего — схема демонстрирует стабильную работу на частотах до 100 МГц. Это максимальная частота, которую мой драйвер Si5351 может генерировать с фазовым сдвигом 90°. Судя по даташиту [PDF] на 74HC4053, в пределе демодулятор должен работать на частотах где-то до 200 МГц. Ищите параметр Fmax, «Minimum Switch Frequency Response at -3dB».
Рассмотренный материал важен для понимания теории. Но в современных устройствах часто применяется другая схема — детектор Тейло.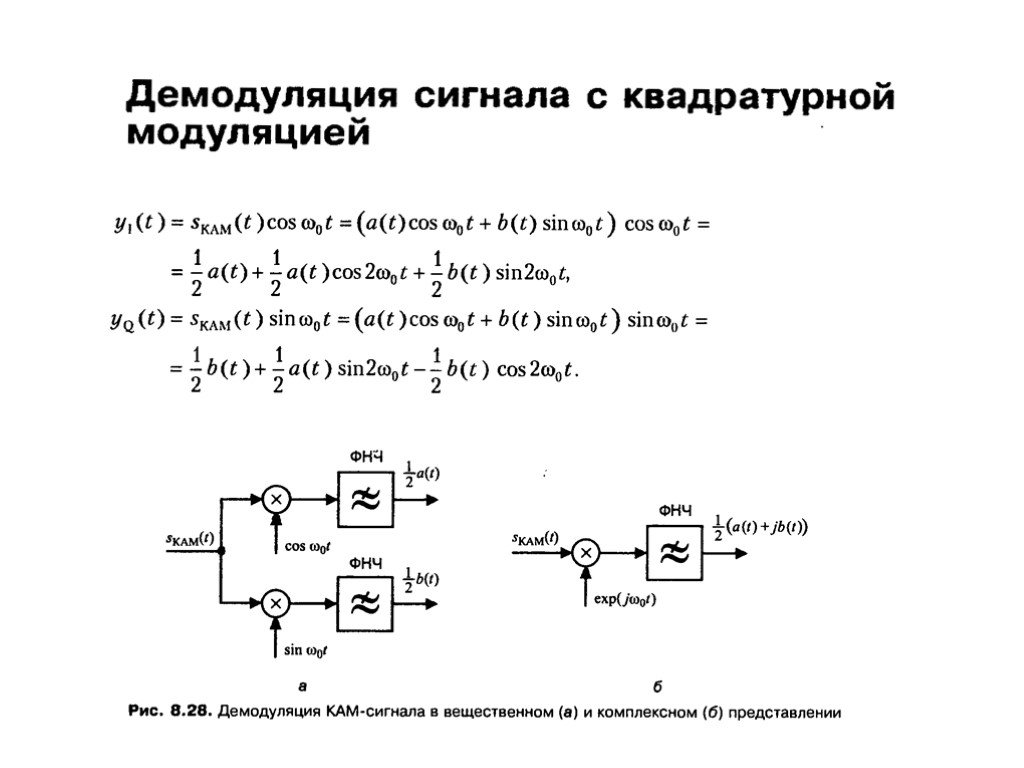
С ним мы познакомимся в другой раз.
Дополнение: В продолжение темы см также пост Сдвиг фазы аудио-сигнала на 90° при помощи ОУ.
Метки: SDR, Беспроводная связь, Любительское радио, Электроника.
Добавлено 24 июня 2018 в 19:00
В данной статье рассматривается использование квадратурной демодуляции с частотно- и фазо-модулированными сигналами.
Из предыдущей статьи мы знаем, что квадратурная демодуляция создает два низкочастотных сигнала, которые взятые вместе передают информацию, которая была закодирована в сигнал несущей принимаемого сигнала. Более конкретно, эти сигналы I и Q эквивалентны действительной и мнимой частям комплексного числа. Низкочастотный сигнал, содержащийся в модулированном сигнале, соответствует представлению «амплитуда-плюс-фаза» исходных данных, а квадратурная демодуляция преобразует это представление «амплитуда-плюс-фаза» в сигналы I и Q, которые соответствуют декартовому представлению.
Возможно, это неудивительно, что мы можем использовать квадратурную демодуляцию для демодуляции амплитудно-модулированных сигналов, учитывая, что квадратурный демодулятор представляет собой просто два амплитудных демодулятора, приводимых в действие опорными сигналами несущей частоты, которые имеют разность фаз 90°. Однако одной из важнейших характеристик квадратурной демодуляции является ее универсальность. Она работает не только с амплитудной модуляцией, но и с частотной и фазовой модуляциями.
Сначала давайте рассмотрим I и Q сигналы, которые получаются при применении квадратурной демодуляции к сигналу с частотной модуляцией. Принимаемый FM сигнал представляет собой несущую 100 кГц, модулированную синусоидой 100 Гц. Мы используем тот же квадратурный демодулятор, который использовался в моделировании амплитудной модуляции; он имеет два источника напряжения с произвольным поведением для выполнения умножения, а за каждым источником напряжения следует двухполюсный фильтр нижних частот (частота среза составляет ~1 кГц).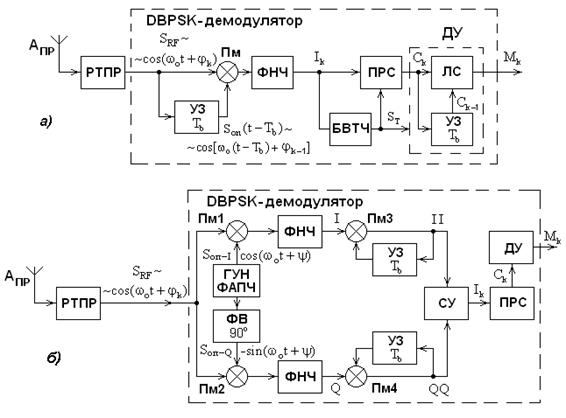
Для получения информации о том, как в LTspice создать FM сигнал, вы можете обратиться к статье «Как демодулировать частотно-модулированный сигнал».
Возможно, распространенной реакцией на эту диаграмму будет замешательство. Как эти странно выглядящие сигналы связаны с синусоидой с постоянной частотой, которая должна получиться в результате процесса демодуляции? Сначала давайте сделаем два замечания:
2)}\), мы извлекаем амплитуду. Проблема в том, что исходные данные были закодированы не в амплитуде несущей – они были закодированы в угле (помните, что частотная и фазовая модуляции являются двумя формами угловой модуляции).Итак, давайте попробуем другую формулу. Давайте извлечем угол из I/Q данных, а не амплитуду. Как показано на рисунке с прямоугольным треугольником выше, мы можем сделать это, применив следующую формулу:
\[ \phi=\text{arctg} \left( \frac{Q}{I} \right) \]
А вот результат:
Диаграмма расчета изменения углаЭто выглядит не очень хорошо, но мы реально становимся ближе к цели. Красный график представляет собой мгновенную фазу исходных данных (обратите внимание, что график кажется более неустойчивым, чем есть на самом деле, потому что угол прыгает от –90° до +90°, или наоборот). Частотная модуляция, хотя и основана на фазе, не кодирует информацию непосредственно в фазе несущей. Скорее она кодирует информацию в мгновенной частоте несущей, а мгновенная частота является производной от мгновенной фазы.
Итак, что произойдет, если взять производную от красного графика?
Как вы можете видеть, теперь мы восстановили сигнал, который является синусоидой и имеет ту же частоту, что и исходный низкочастотный сигнал.
На этом этапе вам может стать интересно, почему кто-то беспокоится об I/Q демодуляции. Как кто-то в мире разработал схему, которая генерирует выходной сигнал, соответствующий производной от арктангенса двух входных сигналов? Ну, чтобы ответить на вопрос, заданный в названии этого раздела, вы оцифровываете сигналы и вычисляете арктангенс в прошивке или программном обеспечении. И это подводит нас к важному вопросу: квадратурная демодуляция особенно выгодна в контексте программно-определяемых радиосистем.
Программно-определяемая радиосистема (SDR, software-defined radio) представляет собой систему беспроводной связи, в которой значительная часть функций передатчика и/или приемника реализована с помощью программного обеспечения.
Квадратурная демодуляция очень универсальна и позволяет одному приемнику почти мгновенно адаптироваться к различным типам модуляции. Однако, выходные I/Q сигналы гораздо менее просты, чем обычный низкочастотный сигнал, создаваемый стандартными схемами демодуляторов. Вот почему квадратурный демодулятор и цифровой сигнальный процессор формируют такую высокопроизводительную систему: цифровой сигнальный процессор может легко применять сложные математические операции к I/Q данным, создаваемым демодулятором.
Те же общие соображения, которые мы обсуждали в контексте квадратурной частотной демодуляции, относятся также к квадратурной фазовой демодуляции. Однако для восстановления исходных данных мы берем арктангенс от (Q/I), а не производную от арктангенса от (Q/I), поскольку низкочастотный сигнал кодируется непосредственно в фазе несущей, а не в производной фазы (т.е. частоте).
Следующий график был получен путем применения квадратурной демодуляции к сигналу с фазовой манипуляцией, состоящему из несущей 100 кГц и цифрового низкочастотного сигнала 100 Гц, который вызывает изменения фазы несущей на 180° в зависимости от того, идет ли он с низким или высоким логическим уровнем.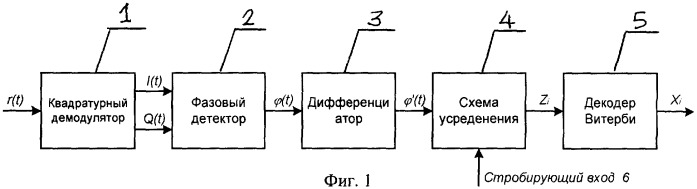
Как вы можете видеть, красный график (значение которого соответствует фазе принимаемого сигнала) воспроизводит логические переходы низкочастотного сигнала.
Обратите внимание, что красный график вычисляется с помощью функции «atan2«. Стандартный арктангенс ограничен двумя квадрантами (т.е. 180°) декартовой плоскости. Функция atan2 смотрит на отдельные полярности входных значений, чтобы создавать углы, охватывающие все четыре квадранта.
atan2» необходима, если система должна иметь возможность воспроизведения полных 360° фазы.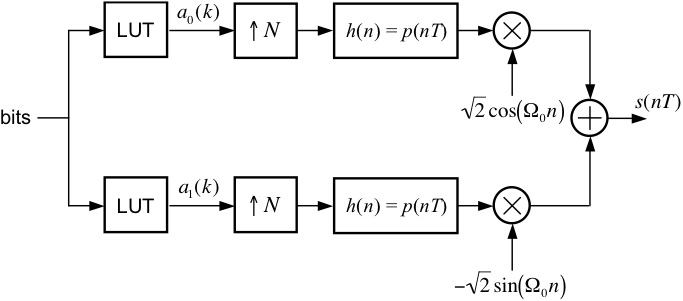
Оригинал статьи:
Назад
Оглавление
к Кен Джентиле Скачать PDF
Цифровые квадратурные модуляторы появляются в ряде ИС связи и обработки сигналов.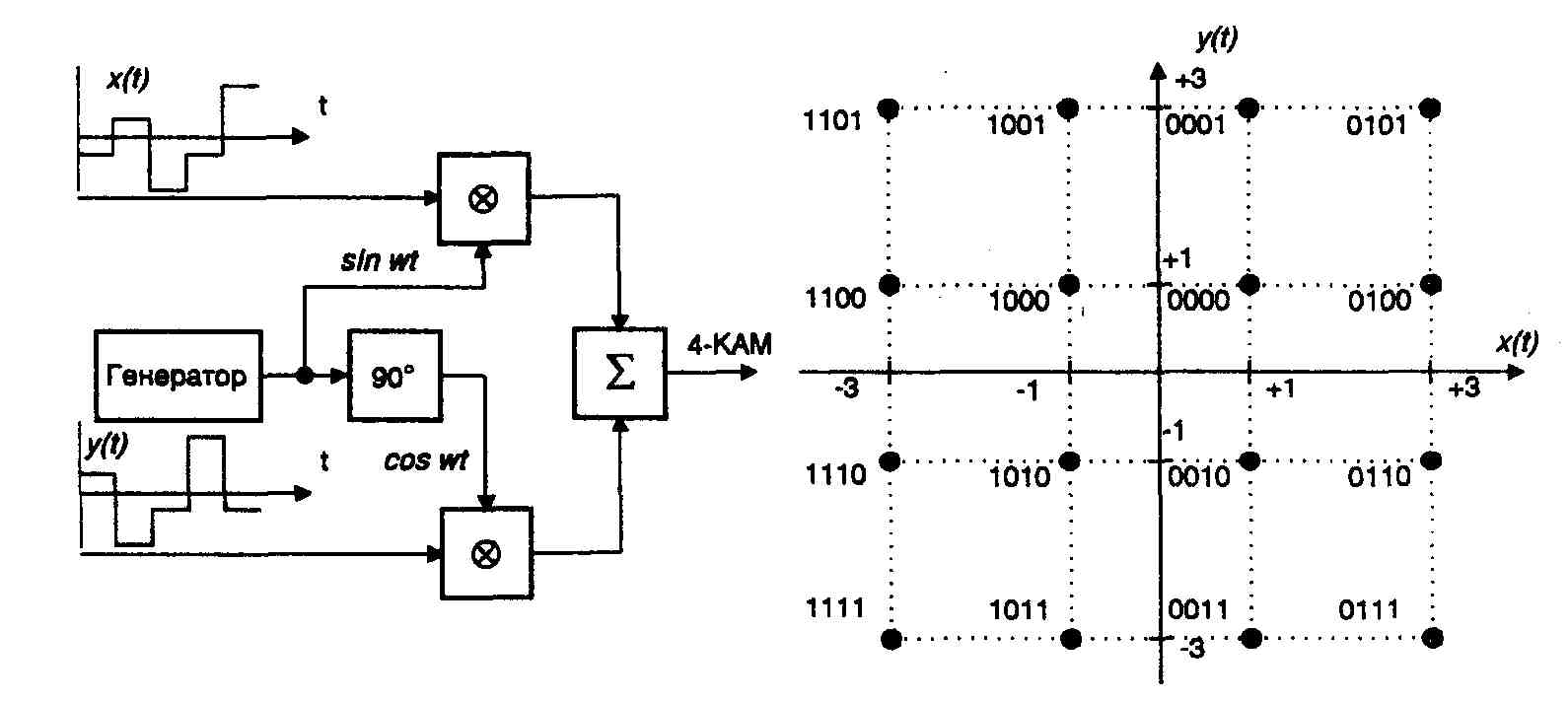
В этих указаниях по применению объясняются основные строительные блоки цифрового квадратурного модулятора и проводится анализ коэффициента усиления модулятора для трех типов входных сигналов.
Универсальный цифровой модулятор состоит из пары цифровых умножителей и цифрового сумматора, сконфигурированных, как показано на рисунке 1. Как правило, все двоичные числа, связанные с путями данных, имеют одинаковый числовой диапазон, а именно ±1. Это относится к входным (I, Q и несущей), выходным (Y) и промежуточным путям данных. Ширина N-битной шины показана на диаграмме для общности, где N битов представляют дробные числовые значения от -1 до +1.
Рис. 1. Функциональная схема цифрового квадратурного модулятора.
Из четырех входов два предназначены для обработки цифрового несущего сигнала, который представляет собой N-битное квантованное представление синусоидальной и косинусоидальной волн, образующих квадратурную несущую. По определению, несущая имеет отдельные компоненты косинуса и синуса, обе из которых колеблются (численно) с частотой несущей в радианах, ω C (где ω C равно 2πf C , где f C обозначает более высокую частоту).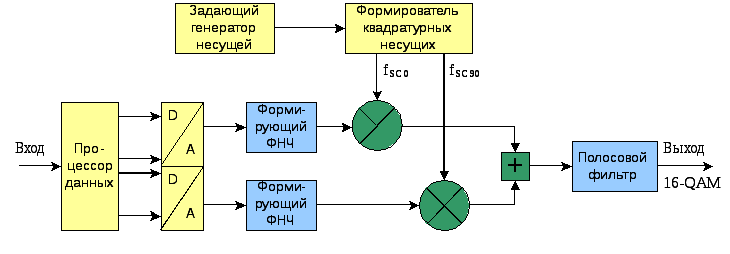
привычные единицы циклов в единицу времени). Два других входа (I и Q) используются для обработки цифрового N-битного квантованного сигнала основной полосы частот. Метки I и Q представляют собой сокращенное обозначение синфазной и квадратурной составляющих, соответственно, сигнала основной полосы частот. Выход Y представляет собой N-битное квантованное цифровое представление сигнала основной полосы частот, преобразованного с повышением частоты в несущую частоту (f С ).
Связь между входным и выходным сигналами может быть выражена как функция времени, как показано в уравнении 1.
Несущий сигнал зависит от времени по определению, на что указывает член t в аргументах функций синуса и косинуса. Членам Y, I и Q также были присвоены аргументы t, что указывает на то, что их значения также могут зависеть от времени. Масштабный коэффициент ½ является следствием использования одинакового количества битов как на входе, так и на выходе сумматора. Причина в том, что сумма двух выходных N-битных умножителей фактически требует N + 1 бит для представления полного диапазона суммированных результатов.
Далее следует анализ выходного сигнала Y(t) для трех различных типов входных сигналов I и Q. Рассматриваемые типы входных сигналов:
Следующему анализу помогают тригонометрические тождества, данные уравнениями 2 и 3. Кроме того, формула, приведенная в уравнении 4, полезна для квадратурного анализа сигналов. Он связывает квадратурное выражение (левая часть) с функцией косинуса (правая часть). Особый интерес представляет применение уравнения 4 к уравнению 1, которое дает альтернативную форму для Y(t), как показано в уравнении 59.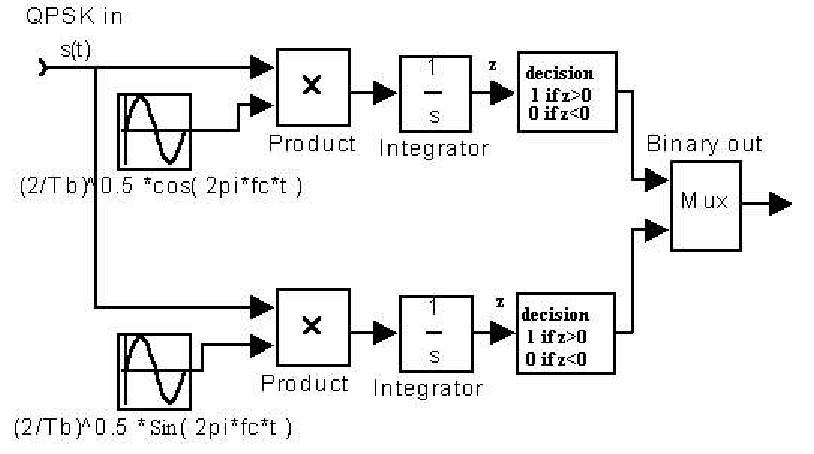
0006
В этом случае входные сигналы I и Q не зависят от времени, а являются статическими числовыми значениями, заданными D и E соответственно. Предполагается, что D и E являются дробными значениями от 0 до 1 включительно, что означает, что они представляют дробную часть максимально возможного пикового входного значения. На основании уравнения 5 Y(t) выражается как
Обратите внимание, что аргумент функции косинуса в уравнении 6 содержит только одну частотную составляющую (ω С ). Это означает, что выходной сигнал представляет собой один тон с той же частотой, что и несущий сигнал. Однако фаза выходного сигнала опережает угол в радианах arctan(E/D) по отношению к фазе косинусной составляющей квадратурного входного сигнала несущей. Кроме того, амплитуда выходного сигнала зависит от векторной суммы D и E. Для уникального случая, когда D и E являются одним и тем же числовым значением (то есть D = E = k (0 ≤ k ≤ 1)) , Y(t) уменьшается до
Поучительно рассмотреть частный случай k = 1; то есть входы I и Q являются статическими значениями полной шкалы.
Когда k = 1, пиковое значение Y(t) равно √2/2. Это представляет усиление -3 дБ относительно максимально возможного пикового выходного значения 1. Нормализованная выходная мощность равна (√2/2) 2 = ½, или -3 дБ относительно максимально возможной выходной мощности (1 ) 2 = 1.
В этом случае входные сигналы I и Q являются синусоидами. Обе синусоиды имеют произвольную частоту основной полосы в радианах, ω B , без относительного сдвига фазы (то есть оба сигнала находятся в фазе друг с другом). Кроме того, сигнал I масштабируется константой A (0 ≤ A ≤ 1), а сигнал Q масштабируется константой B (0 ≤ B ≤ 1). На основании уравнения 5 выходной сигнал выражается как
Это упрощается до
Обратите внимание, что, как и в случае статического входного сигнала, несущая имеет постоянный фазовый сдвиг, определяемый как θ = arctan(B/A).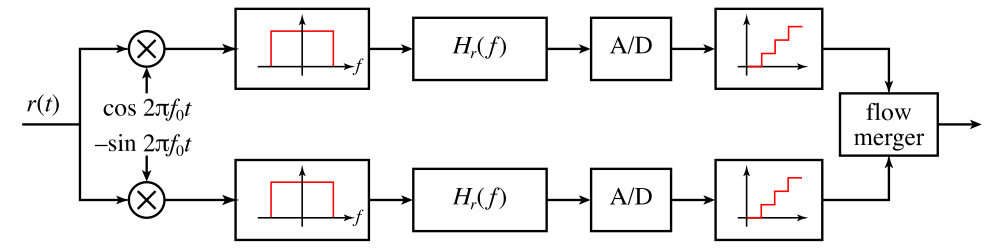
Применение уравнения 2 к форме Y(t) в уравнении 9 приводит к
Обратите внимание, что Y(t) состоит из двух функций косинуса. Одна из функций косинуса содержит член частоты в радианах ω C + ω B , а другая содержит член частоты в радианах ω C — ω B ; однако обе функции демонстрируют фазовый сдвиг θ = arctan(B/A). Таким образом, Y(t) состоит из двух тонов, оба смещены от несущей частоты (f C ) на частоту основной полосы частот (f В ). Кроме того, каждый тон масштабируется по амплитуде на величину
. Поучительно рассмотреть случай A = B = 1; то есть сигналы I и Q имеют пиковые значения, которые охватывают полный диапазон входного сигнала. В этом случае пиковое значение каждого выходного тона становится равным √2/4, а сдвиг фазы (θ) становится равным π/4 радиана. Обратите внимание, что пиковое значение √2/4 представляет усиление на -9 дБ относительно максимально возможного пикового выходного значения 1.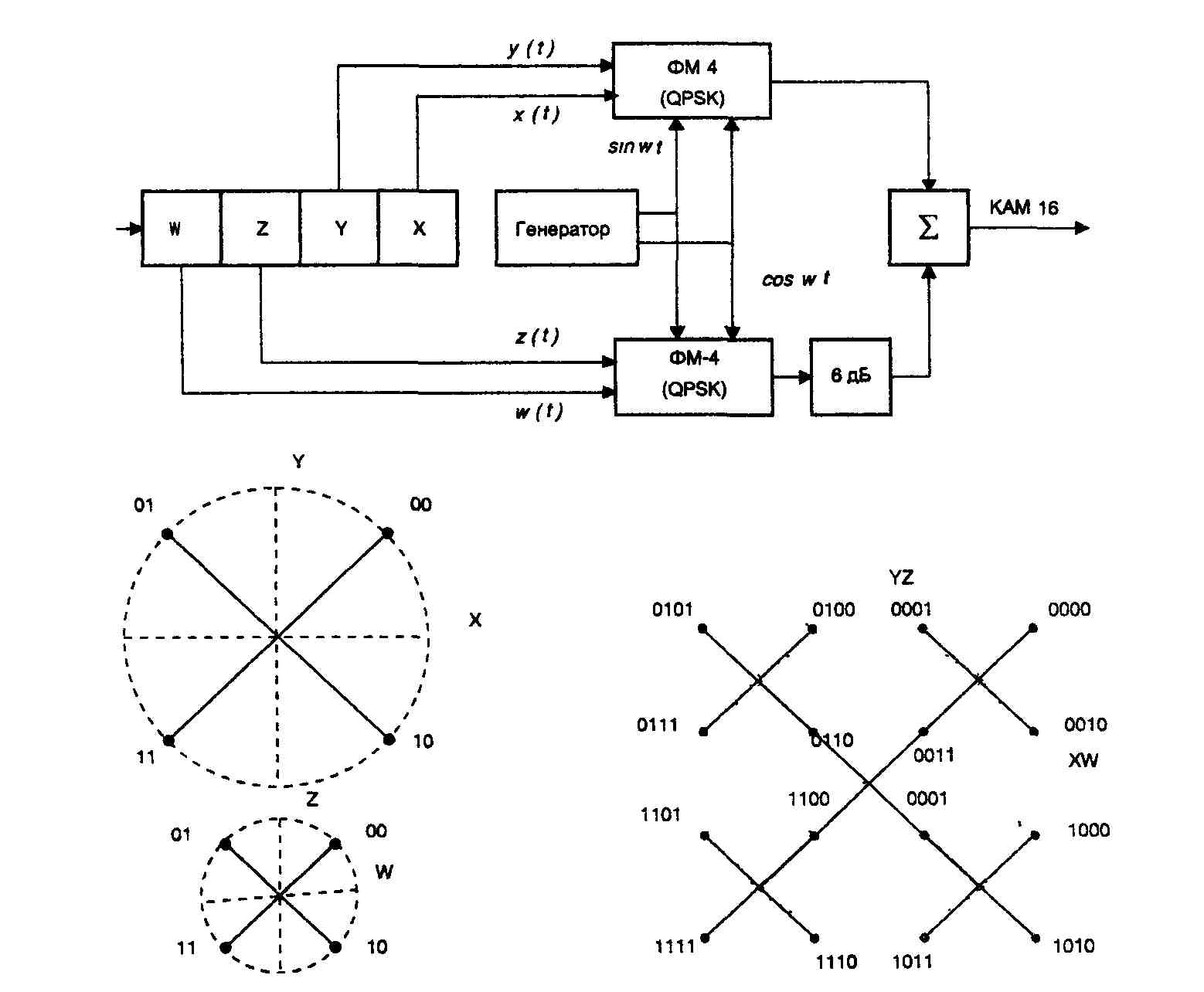
Нормализованная мощность каждого тона равна (√2/4) 2 = ⅛. Поскольку общая мощность представляет собой сумму мощности каждого тона, общая мощность равна ¼. Следовательно, Y(t) демонстрирует потери мощности на 6 дБ относительно максимально возможной выходной мощности (1) 2 = 1 (мощность одиночной синусоиды с пиковым значением 1).
Обратите внимание, что если входные сигналы заменить синусоидальными функциями, результаты будут такими же, как и здесь, за исключением того, что Y(t) будет содержать синусоидальные функции.
В этом случае входные сигналы I и Q составляют квадратурный тон (функции косинуса и синуса соответственно) с частотой модулирующих сигналов в радианах ω B .
Сигнал I масштабируется по A (0 ≤ A ≤ 1), а сигнал Q масштабируется по B (0 ≤ B ≤ 1). На основании уравнения 1 Y(t) выражается как
Применение уравнения 2 и уравнения 3 к форме Y(t), показанной в уравнении 12, а затем упрощение уравнения приводит к
Обратите внимание, что Y(t) содержит только один член косинуса, подразумевая, что Y(t) состоит из одного тона. Его частота в радианах представляет собой сумму частоты в радианах базовой полосы (ω B ) и частоты несущей в радианах (ω C ) с амплитудой тона, масштабированной на ½ AB.
Поучительно рассмотреть случай A = B = 1; то есть сигналы I и Q имеют пиковые значения, которые охватывают полный диапазон входного сигнала. В этом случае Y(t) принимает следующий вид:
Обратите внимание, что пиковая амплитуда выходного сигнала одиночного тона составляет ½. Это представляет усиление -6 дБ относительно максимально возможного пикового выходного значения 1. Нормализованная выходная мощность равна (½) 2 = ¼, что представляет собой потерю мощности 6 дБ относительно максимально возможной выходной мощности ( 1) 2 = 1.
В предыдущих разделах было показано, что N-разрядный цифровой квадратурный модулятор имеет собственное затухание, которое зависит от типа сигнала, подаваемого на входы I и Q. Коэффициенты затухания для трех типов входных сигналов приведены в следующем списке:
Внутреннее затухание, создаваемое цифровым квадратурным модулятором, можно преодолеть, включив цифровой умножитель на выходе модулятора. Умножитель служит усилителем для компенсации собственного затухания модулятора. Величина усиления, которую можно допустить без числового переполнения, зависит от амплитуды входных сигналов I и Q. Однако для полномасштабных входных сигналов I и Q необходимо наложить верхнюю границу на коэффициент усиления, чтобы предотвратить числовое переполнение. Когда входной сигнал представляет собой квадратурный тон, коэффициент усиления должен быть ограничен до 2,0 (или 6 дБ).
Когда входной сигнал является либо неквадратурным тоном, либо статическим значением, коэффициент усиления должен быть ограничен до 1,414 (или 3 дБ).
Внутреннее затухание, создаваемое N-разрядным цифровым квадратурным модулятором, приводит к потере мощности сигнала по сравнению с мощностью полномасштабного N-разрядного синусоидального тона. Степень потери мощности зависит от типа сигнала, подаваемого на входы I и Q. Относительная выходная мощность для трех типов входных сигналов представлена в следующем списке:
Потери мощности, связанные с различными типами входных сигналов (см. рис. 2), очевидны, когда модулятор управляет ЦАП, а анализатор спектра подключен к выходу ЦАП для измерения мощности сигнала. Поскольку модулятор имеет N-битный выходной сигнал, эталонная мощность является мощностью N-битного квантованного синусоидального тона.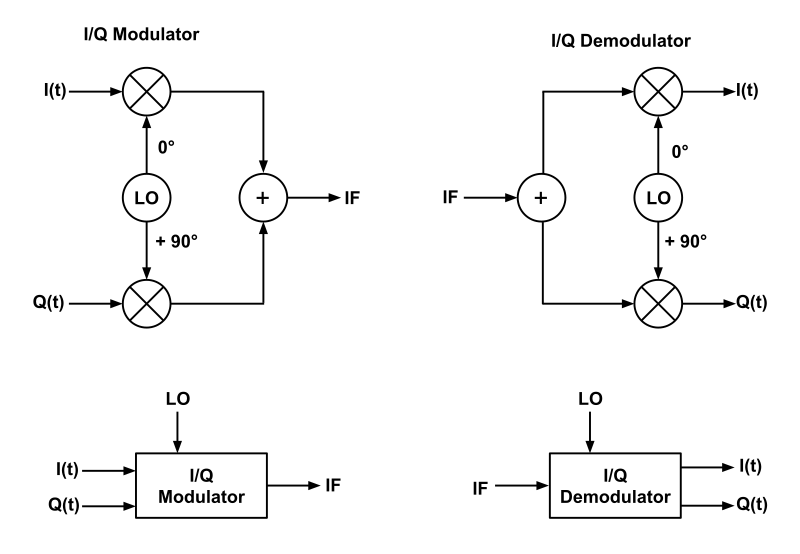
Уровень мощности такого тона, измеренный анализатором спектра, является эталонным уровнем для последующего обсуждения и обозначается как 0 дБр.
Рисунок 2. Спектр относительной мощности.
При использовании N-битного цифрового модулятора, управляющего N-битным ЦАП (как показано на рис. 1), выходная мощность зависит от типа сигнала, подаваемого на входы I и Q. В частности, когда входы I и Q модулятора управляются полномасштабным статическим входным сигналом, выход ЦАП представляет собой одиночный тон на несущей частоте (f C ) с уровнем выходной мощности -3 дБр. . Когда входы I и Q модулятора управляются полномасштабным квадратурным тоном, выход ЦАП представляет собой одиночный тон с частотой f C + f B с уровнем выходной мощности -6 дБр. Когда входы I и Q модулятора управляются полномасштабным неквадратурным тоном, выход ЦАП состоит из двух частот (f C ± f B ) с уровнем выходной мощности -9 дБр для каждой тон.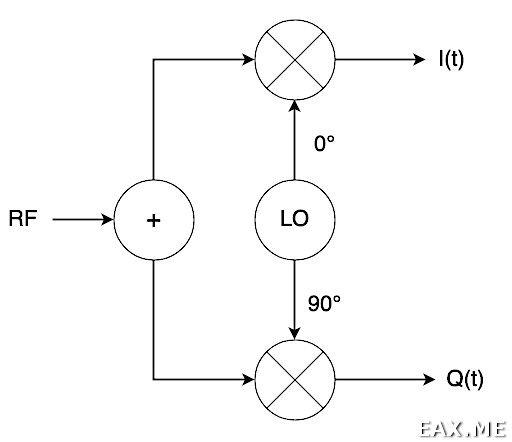
Мощность композитного сигнала (оба тона объединены) составляет -6 дБр, что в два раза превышает мощность любого из выходных тонов.
Кен Джентиле
Кен Джентиле присоединился к Analog Devices в 1998 году в качестве инженера-проектировщика систем линейки продуктов Clock and Signal Synthesis в Гринсборо, Северная Каролина, где он специализируется на прямом цифровом синтезе, проектировании аналоговых фильтров и написании инженерных инструментов на основе графического интерфейса пользователя в MATLAB. Кен имеет 10 патентов. Он опубликовал 14 статей в различных отраслевых журналах и более дюжины заметок по применению ADI, а также выступал на ежегодной общей технической конференции ADI (GTC) в 2001, 2005 и 2006 годах.96 с B.S.E.E. из Университета штата Северная Каролина. В свободное время Кен любит читать, решать математические головоломки и почти все, что связано с наукой, инженерией и астрономией «на заднем дворе».
Модулятор и демодулятор QAM объединяют два сигнала амплитудной модуляции в один канал передачи данных. Метод изменения любой характеристики (амплитуды, частоты или фазы) относительно высокочастотного несущего сигнала пропорционально мгновенному значению модулирующего сигнала или сигнала сообщения известен как модуляция. Например, сигналы входных данных I и Q модулируются по амплитуде синусоидальной и косинусоидальной несущей соответственно. Два модулированных сигнала объединяются, а затем обрабатываются в соответствии со спецификациями РЧ. Затем эти сигналы преобразовываются по частоте, и выполняется усиление для удовлетворения окончательных критериев частоты и амплитуды.
Напротив, при демодуляции сигналы от передатчика поступают на демодулятор и разделяются на два сигнала, которые передаются в отдельные микшеры. Гетеродин генерирует необходимые сигналы частотной демодуляции, которые являются синфазными и квадратурными сигналами.
QAM — это технология модуляции, которая объединяет два амплитудно-модулированных сигнала в один канал, что удваивает полосу пропускания системы. QAM также известен как квадратурное мультиплексирование несущей, поскольку два сигнала модулируются и транслируются на приемник одновременно.
Где m1 (t) и m2 (t) — это сигналы сообщений, которые должны передаваться по каналу, а PLL означает фазовую автоподстройку частоты.
QAM, с другой стороны, может использоваться как в аналоговых, так и в цифровых методах модуляции. Цифровой анализ модуляторов QAM с использованием кода «Verilog HDL» и «компилятора RTL».
Концепция доставки цифровой информации с использованием аналоговых сигналов при успешном использовании пропускной способности канала привела к внедрению в беспроводных приложениях новой технологии модуляции, известной как квадратурная амплитудная модуляция (QAM). QAM — это метод модуляции, который используется для передачи цифровых данных между двумя точками при использовании аналоговых сигналов.
Квадратурная амплитудная модуляция (QAM) — это метод передачи данных и информации через несущий сигнал, такой как сигнал LTE. Чтобы получить более высокие скорости передачи данных и максимизировать спектральную эффективность, сигнал/символ должен нести как можно больше данных.
«QAM достигает этой цели за счет увеличения количества различных форм сигнала, при этом каждая форма сигнала или созвездие кодирует отдельное двоичное число». Существуют схемы 16-QAM, 64-QAM и 256-QAM в беспроводная и проводная связь, а также более высокие схемы QAM, такие как 1024-QAM, которые в настоящее время изучаются для будущего роста LTE/LTE-Advanced Pro и 5G.
OFDM является эффективной схемой модуляции, используемой в современных системах беспроводной связи, таких как 5G. OFDM — это метод связи с высокой скоростью передачи данных, который сочетает в себе преимущества квадратурной амплитудной модуляции (QAM) с мультиплексированием с частотным разделением (FDM). Таким образом, в растущей технологии 5G мы можем ожидать использования размеров созвездия сигналов QAM в диапазоне от 256 (8 бит на символ) до 1024 (10 бит на символ).
Квадратурная амплитудная модуляция Помимо увеличения пропускной способности канала, QAM имеет ряд других преимуществ, которые указаны ниже.
