
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
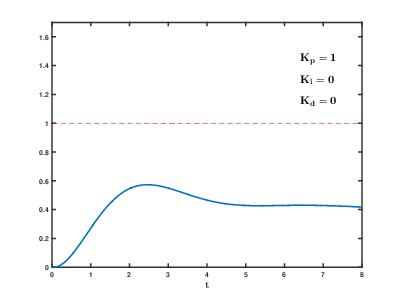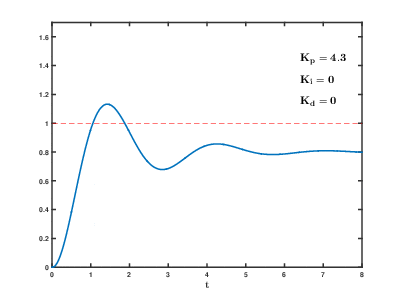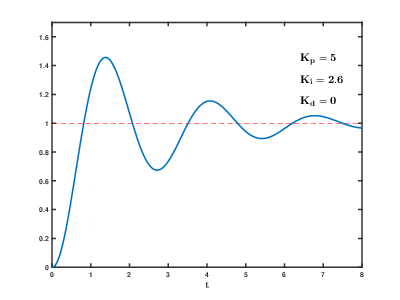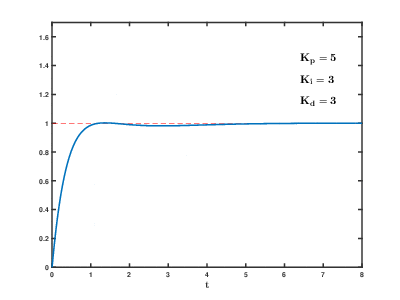
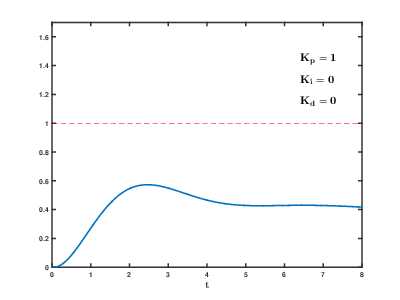 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.
Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0
называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
wikipedia.green
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.
Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
wiki.sc
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.
Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
wiki2.red
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
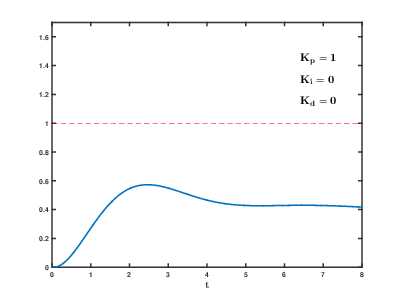 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.
Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
xn--b1aeclack5b4j.xn--j1aef.xn--p1ai
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
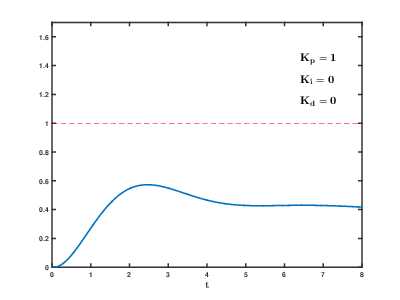 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.
Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
wikiredia.ru
Материал из Википедии — свободной энциклопедии
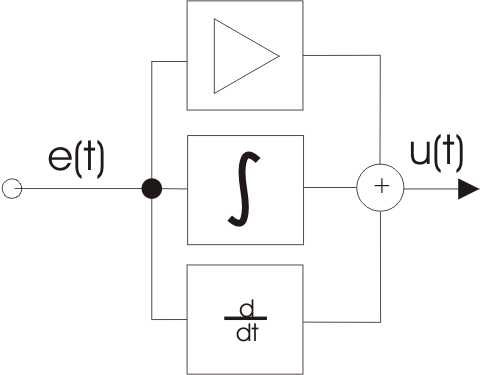 Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:
В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:
где <math>T</math> — время дискретизации. Используя замену <math>K^{discr}_i=K_p K_{ip}T, K^{discr}_d=\frac{K_p K_{dp}}{T}</math> можно записать:
В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае регулятор выходной управляющий сигнал используется для широтно-импульсной модуляции.
В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.
Друзья молчали. Ни тот, ни другой не начинал говорить. Пьер поглядывал на князя Андрея, князь Андрей потирал себе лоб своею маленькою рукой.
– Пойдем ужинать, – сказал он со вздохом, вставая и направляясь к двери.
Они вошли в изящно, заново, богато отделанную столовую. Всё, от салфеток до серебра, фаянса и хрусталя, носило на себе тот особенный отпечаток новизны, который бывает в хозяйстве молодых супругов. В середине ужина князь Андрей облокотился и, как человек, давно имеющий что нибудь на сердце и вдруг решающийся высказаться, с выражением нервного раздражения, в каком Пьер никогда еще не видал своего приятеля, начал говорить:
– Никогда, никогда не женись, мой друг; вот тебе мой совет: не женись до тех пор, пока ты не скажешь себе, что ты сделал всё, что мог, и до тех пор, пока ты не перестанешь любить ту женщину, какую ты выбрал, пока ты не увидишь ее ясно; а то ты ошибешься жестоко и непоправимо. Женись стариком, никуда негодным… А то пропадет всё, что в тебе есть хорошего и высокого. Всё истратится по мелочам. Да, да, да! Не смотри на меня с таким удивлением. Ежели ты ждешь от себя чего нибудь впереди, то на каждом шагу ты будешь чувствовать, что для тебя всё кончено, всё закрыто, кроме гостиной, где ты будешь стоять на одной доске с придворным лакеем и идиотом… Да что!…
Он энергически махнул рукой.
Пьер снял очки, отчего лицо его изменилось, еще более выказывая доброту, и удивленно глядел на друга.
– Моя жена, – продолжал князь Андрей, – прекрасная женщина. Это одна из тех редких женщин, с которою можно быть покойным за свою честь; но, Боже мой, чего бы я не дал теперь, чтобы не быть женатым! Это я тебе одному и первому говорю, потому что я люблю тебя.
Князь Андрей, говоря это, был еще менее похож, чем прежде, на того Болконского, который развалившись сидел в креслах Анны Павловны и сквозь зубы, щурясь, говорил французские фразы. Его сухое лицо всё дрожало нервическим оживлением каждого мускула; глаза, в которых прежде казался потушенным огонь жизни, теперь блестели лучистым, ярким блеском. Видно было, что чем безжизненнее казался он в обыкновенное время, тем энергичнее был он в эти минуты почти болезненного раздражения.
– Ты не понимаешь, отчего я это говорю, – продолжал он. – Ведь это целая история жизни. Ты говоришь, Бонапарте и его карьера, – сказал он, хотя Пьер и не говорил про Бонапарте. – Ты говоришь Бонапарте; но Бонапарте, когда он работал, шаг за шагом шел к цели, он был свободен, у него ничего не было, кроме его цели, – и он достиг ее. Но свяжи себя с женщиной – и как скованный колодник, теряешь всякую свободу. И всё, что есть в тебе надежд и сил, всё только тяготит и раскаянием мучает тебя. Гостиные, сплетни, балы, тщеславие, ничтожество – вот заколдованный круг, из которого я не могу выйти. Я теперь отправляюсь на войну, на величайшую войну, какая только бывала, а я ничего не знаю и никуда не гожусь. Je suis tres aimable et tres caustique, [Я очень мил и очень едок,] – продолжал князь Андрей, – и у Анны Павловны меня слушают. И это глупое общество, без которого не может жить моя жена, и эти женщины… Ежели бы ты только мог знать, что это такое toutes les femmes distinguees [все эти женщины хорошего общества] и вообще женщины! Отец мой прав. Эгоизм, тщеславие, тупоумие, ничтожество во всем – вот женщины, когда показываются все так, как они есть. Посмотришь на них в свете, кажется, что что то есть, а ничего, ничего, ничего! Да, не женись, душа моя, не женись, – кончил князь Андрей.
wiki-org.ru
Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра. ПИД-регулятор измеряет отклонение стабилизируемой величины от заданного значения (уставки) и выдаёт управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально этому отклонению, второе пропорционально интегралу отклонения и третье пропорционально производной отклонения (или, что то же самое, производной измеряемой величины).
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п.
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен уставке, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к уставке, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь уставки, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Для устранения статической ошибки используют интегральную составляющую. Она позволяет регулятору «учиться» на предыдущем опыте. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая.
Дифференциальная составляющая противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Эти отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Чем быстрее регулируемая величина отклоняется от уставки, тем сильнее противодействие, создаваемое дифференциальной составляющей.
Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется уставкой, а разность e = (x0 − x) — невязкой или рассогласованием.
Выходной сигнал регулятора u определяется тремя слагаемыми:
где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие:
Часто в качестве параметров ПИД-регулятора используются:
Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: ПИД-регулятор. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
vlab.wikia.org