Пример rsa алгоритм: Выбор параметров шифра RSA и возможные последствия / Хабр

Выбор параметров шифра RSA и возможные последствия / Хабр

Под катом описаны примеры выбора «плохих» параметров шифра RSA.

Процитируем авторов учебного пособия «Основы криптографии» А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин, Москва. «Гелиос АРВ», 2001г., на странице 316:

«Следует подчеркнуть необходимость соблюдения осторожности в выборе модуля RSA (числа n) для каждого из корреспондентов сети. В связи с этим можно сказать следующее. Читатель может самостоятельно убедиться в том, что зная одну из трех величин p, q или φ(n), можно легко найти секретный ключ RSA…».

Дополним этот текст. При неудачном выборе модуля шифра RSA, как это сделано в примере пособия, приводимом ниже, можно дешифровать текст и без наличия секретного ключа, т.е. не зная ни одной из трех названных величин.

Для этого достаточно располагать зашифрованным текстом, заданным модулем шифра n, открытым ключом е шифра и выполнить всего три шага атаки «бесключевого чтения». После четвертого атакующего шага устанавливается, что на предыдущем шаге был получен исходный текст, он может быть прочитан. Покажем, насколько просто это делается.

Вначале приведем сам пример со стр. 313-315 из названного пособия.

Пример

Шифрование короткого исходного текстового сообщения: RSA.
Получатель устанавливает шифр с характеристиками n=pq=527, где р=17, q=31 и φ(n)=(р –1)(q – 1)=480. В качестве открытого ключа е выбрано число, взаимно простое с φ(n), е=7. Для этого числа с помощью расширенного алгоритма Евклида найдены целые числа u и v, удовлетворяющие соотношению е∙u+φ(n)∙v=1:

480=7∙68+4,
7=4∙1+3,
4=3∙1+1,
1=4–3∙1=4–(7–4∙1)∙1=4∙2–7∙1=(480–7∙68)∙2–7∙1=480∙2–7∙137,
v=2, u=–137.

Поскольку –137≡343(mod480), то d=343.

Проверка: 7∙343=2401≡1(mod480).

Текстовое сообщение представляется в виде последовательности чисел, содержащихся в интервале [0, 526]. Для этого буквы R, S и

A кодируются пятиразрядными двоичными числами. Используются порядковые номера этих букв в английском алфавите при их двоичном представлении:

R=18₁₀=(10010)₂, S=19₁₀=(10011)₂,
A=1₁₀=(00001)₂.

Тогда RSA=(100101001100001)₂. Разбиение текста на блоки ограниченной длины дает представление из двух блоков: RSA=(100101001), (100001)=(М₁=297, М₂=33).

Последовательно шифруются блоки исходного текста М₁=297, М₂=33:
y₁=Е_k(М₁)=М₁^e≡297⁷(mod527)=474.

Здесь воспользовались тем, что:

297⁷=((297²)³)297≡(mod527)=(200³(mod527)297)(mod527)=474,
y₂=Е_k(М₂)=M₂^e≡33⁷(mod527)=407.

Шифрованный текст, как и исходный, получаем в виде двух блоков: у₁=474; у₂=407.

Расшифрование представляется последовательностью действий D_k(y_i )=(y_i )^d=(y_i )³⁴³(mod 527), i=1,2.

Вычисления возведения в степень d более удобно проводить, предварительно представляя показатель степени суммой степеней числа 2, а именно: 343=256+64+16+4+2+1.

Используя это представление показателя степени d=343, получаем:

474²≡174(mod527),
474⁴≡237(mod527),
474⁸≡307(mod527),
474¹⁶≡443(mod527),
474³²≡205(mod527),
474⁶⁴≡392(mod527),
474¹²⁸≡307(mod527),
474²⁵⁶≡443(mod527),

и окончательно 474³⁴³(mod527)=(443∙392∙443∙237∙174∙474) (mod527)=297.

Аналогично вычисляется значение 407³⁴³(mod527)=33.

Переход к буквенному представлению расшифрованного сообщения дает: RSA.

После рассмотрения примера в пособии приводятся рассуждения о стойкости системы RSA. Подчеркивается необходимость соблюдения осторожности в выборе модуля шифра RSA (числа n) для каждого из корреспондентов сети. Указывается на недопустимость игнорирования требований к выбираемым характеристикам системы шифрования. Среди таких требований, к сожалению, не указано то, нарушение которого иллюстрирует приведенный пример.

Атака на шифр RSA

Рассмотрим пример атаки на шифр RSA. Воспользуемся данными примера, приведенного на странице 313-315 в учебном пособии «Основы криптографии» А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин, Москва. «Гелиос АРВ», 2001.

Неудачность (недопустимость) выбранных параметров системы в этом примере легко показывается вычислениями, реализующими атаку бесключевого чтения исходного текста. Сущность такой атаки состоит в следующем. Заданы открытый ключ шифра RSA (е=7, n=527) и шифрованный текст. В примере шифрованный текст представлен двумя блоками
у=(у₁=474, у₂=407).

Каждый шифрованный блок атакуется индивидуально, вначале атакуем у₁=474, после его дешифрования, атакуем другой блок у₂=407.

Далее формируется путем многократного зашифрования с сохранением результатов двух последовательных шагов алгоритма атаки и с использованием открытого ключа последовательность числовых значений у_i, у₁=у имеющийся шифрованный текст.

В алгоритме атаки на шифрованный текст определяется такой номер шага j, для которого y_i^ej(mod n)=(y_i^ej–1(mod n))^e(mod n)=y_i, i>1. Из последнего соотношения видим, что при возведении в степень е значения (y_i^ej–1(mod n)) получается начальный шифoртекст y_i = у₁.

Но это и означает, что на этом шаге шифровался открытый текст. Непосредственными вычислениями (их оказывается совсем немного) с использованием экранного калькулятора находим то значение j, при котором цикл шифрования завершается значением y₁, с которого цикл и был начат.

Атака на первый блок у₁=474 шифртекста.
Шаг 1: &nbsp 474⁷(mod527)=382

;
Шаг 2: &nbsp 382⁷(mod527)=423;
Шаг 3: &nbsp 423⁷(mod527)=297;
Шаг 4: &nbsp на этом шаге шифруется уже найденный исходный текст, но его необходимо выполнить, так как атакующий исходного текста не знает. Признаком завершения атаки является совпадение начального значения шифртекста (474) и результата 4-го шага зашифрования. Именно такое совпадение и имеет место.

297⁷(mod527)=474 получили начальный (первый) блок шифртекста. Атака на первый блок завершена успешно у₁=474. Предшествующий результат шага 3 равен открытому тексту М₁=297.

По существу в кольце вычетов по модулю n=527 реализовался короткий цикл обработки вычета r=297 по модулю n=527

. Это записывается так y_i=у₁=297. Формируем степенные вычеты
(((297⁷(mod527))⁷(mod527))⁷(mod527))⁷=297.

Атака на второй блок у₂=407 шифртекста.
Шаг 1: &nbsp 407⁷(mod527)=16;
Шаг 2: &nbsp 16⁷(mod527)=101;
Шаг 3: &nbsp 101⁷(mod527)=33;
Шаг 4: &nbsp 33⁷(mod527)=407.

Вновь на третьем шаге получен блок исходного текста (М₂=33), но атакующему это неизвестно, и он выполняет следующий (четвертый шаг), результат которого (407) совпадает с начальным шифртекстом у₂=407.

По существу в кольце вычетов по модулю n=527 реализовался короткий цикл обработки вычета r=33 по модулю n=527.

Это записывается так y_i=у₂=33.
Формируем степенные вычеты ((33⁷(mod527))⁷(mod527))⁷(mod527)=33.

Результат атаки (исходный текст М₁=297, М₂=33) получен трехкратным шифрованием заданного шифртекста. Больший успех для атакующего шифртекст трудно представить.

Продолжая обсуждение вопроса о выборе модуля и других параметров шифра, можно добавить, что модуль шифра (n=527) некоторые исходные тексты вообще не позволяет шифровать. При этом выбор значения открытого ключа е большой роли не играет. Существуют значения исходных текстов, которые вообще невозможно зашифровать выбранным шифром с модулем n=527.

Ни на одном из заданных е не удается зашифровать исходные тексты, представляемые числами
187, 341, 154 и 373.

Пример (невозможность шифрования значений некоторых исходных текстов)

Пусть исходные тексты представлены четырьмя блоками y=(y₁=154, y₂=187, y₃=341, y₄=373). Экспонента е открытого ключа шифра может быть любым взаимно простым числом с функцией Эйлера φ(n)=φ(527)=480. Впрочем, для рассматриваемого случая открытый ключ е может быть задан произвольно. Действительно, пусть е=2, 4, 7, 9, 17, 111 тогда:

154²(mod527)=1;
154⁴(mod527)=1;
154⁷(mod527)=154;
154⁹(mod527)=154;
154¹⁷(mod527)=154;
154¹¹¹(mod527)=154;
187²(mod527)=187;
187⁴(mod527)=187;
187⁷(mod527)=187;
187⁹(mod527)=187;
187¹⁷(mod527)=187;
187

111(mod527)=187;
341²(mod527)=341;
341⁴(mod527)=1;
341⁷(mod527)=341;
341⁹(mod527)=341;
341¹⁷(mod527)=341;
341¹¹¹(mod527)=341;
373²(mod527)=1;
373⁴(mod527)=373;
373⁷(mod527)=373;
373⁹(mod527)=373;
373¹⁷(mod527)=373;
373¹¹¹(mod527)=373.

Из рассмотренного примера следует простой вывод. Действительно, к выбору параметров процесса шифрования надо подходить очень внимательно и проводить тщательный предварительный анализ таких параметров. Как это делать — отдельный вопрос, и в рамках этой работы он не рассматривается.

Пример алгоритма шифрования rsa | Защита информации

06.10.2015

Содержание:

• Шаги алгоритма RSA
• Пример: шифрование сообщения с помощью RSA
• Схема Рабина

Алгоритм RSA

Допустим, что объект А хочет передать сообщение объекту В в зашифрованном виде. Для этого используем алгоритм RSA. При передаче могут возникнут проблемы из-за характеристики проводных линий связи или плохую полосу пропускания и пропускную способность. Для этого нужно использовать методы обнаружения ошибок. Но для разных сетей разные методы.

Шаги:

• объект В придумывает два любых больших простых числа Р и Q;
• объект В решает значение модуля N = P × Q;
• объект В решает функцию Эйлера:φ(N) = (P-1) × (Q-1);
  и выбирает любым образом значение открытого ключа K_в с учетом условия:1 < K_в ≤ φ(N), НОД (K_в, φ(N)) = 1
• объект В решает значение секретного ключа κ_в решая алгоритм Евклида когда достигается условие: κ_в ≡ K_в^-1 (mod φ(N)).
• объект В передает объекту А пару числе (N, K_в) по незащищенному пути.
• Если объект А хочет передать объекту В сообщение М, он должен разбить исходный открытый текст M на блоки, каждый из которых может быть показан в виде: M_i = 0, 1, 2, …, N — 1.
• Объект А шифрует данные, показаны в виде последовательности чисел M_i по формуле: C_i = M_i^K_в (mod N), и отправляет криптограмму C₁, C₂, …, C_i … объекту В.
• Пользователь В расшифровывает криптограмму C₁, C₂, …, C_i … используя секретный ключ κ_в по формуле: M_i = C_i^K_в (mod N)

При реализации алгоритма на практике, нужно иметь возможность без сильных затрат генерировать большие простые числа, к тому же быстро решать значение ключей.

Пример: шифрование сообщения

Для наглядности вычисления, будем использовать небольшие числа.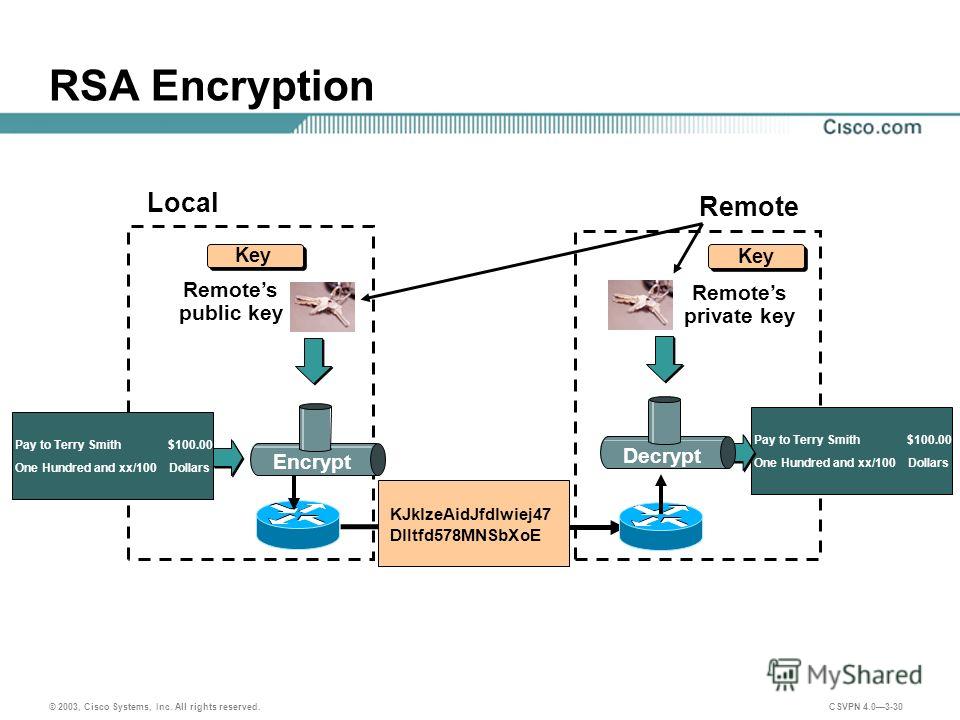 Но на практике используют очень большие числа ( длиной 200-300 десятичных разрядов).

Действия объекта В:

• Берет Р = 3, Q = 11.
• Берет модуль N = P × Q = 3 × 11 = 33.
• Берет значение функции Эйлера для N = 33: φ(N) = (P-1) × (Q-1) = 2 × 10 = 20.
• Берет в качестве открытого ключа K_в произвольное число с учетом условия: 1 < K_в ≤ φ(N), НОД (K_в, φ(N)) = 1, допустим K_в = 7.
• Решаем значение секретного ключа κ_в используя алгоритм Евклида: κ_в ≡ = 3.
• объект В передает объекту А пару чисел (N = 33, K_в = 7).

Действия объекта A:

• Показывает шифруемое сообщение как последовательность целых чисел в диапазоне 0…32. Допустим буква А представляется как число 1, буква В это 2 и С = 3. Припустим что сообщение С А В можно показать как последовательность числе 321, то есть M₁ = 3, M₂ = 1, M₃ = 2.
• Шифрует сообщение, М используя ключ K_в = 7 и N = 33 по формуле: C_i = M_i^K_в (mod N) = M_i⁷(mod 3).
• Получаем:
  • C_i = 3⁷(mod 33) = 2187 (mod 33) = 9
  • C_i = 1⁷(mod 33) = 1 (mod 33) = 1
  • C_i = 2⁷(mod 33) = 128 (mod 33) = 29
• Передает объекту В криптограмму: C₁, C₂, C₃ = 9, 1, 29.

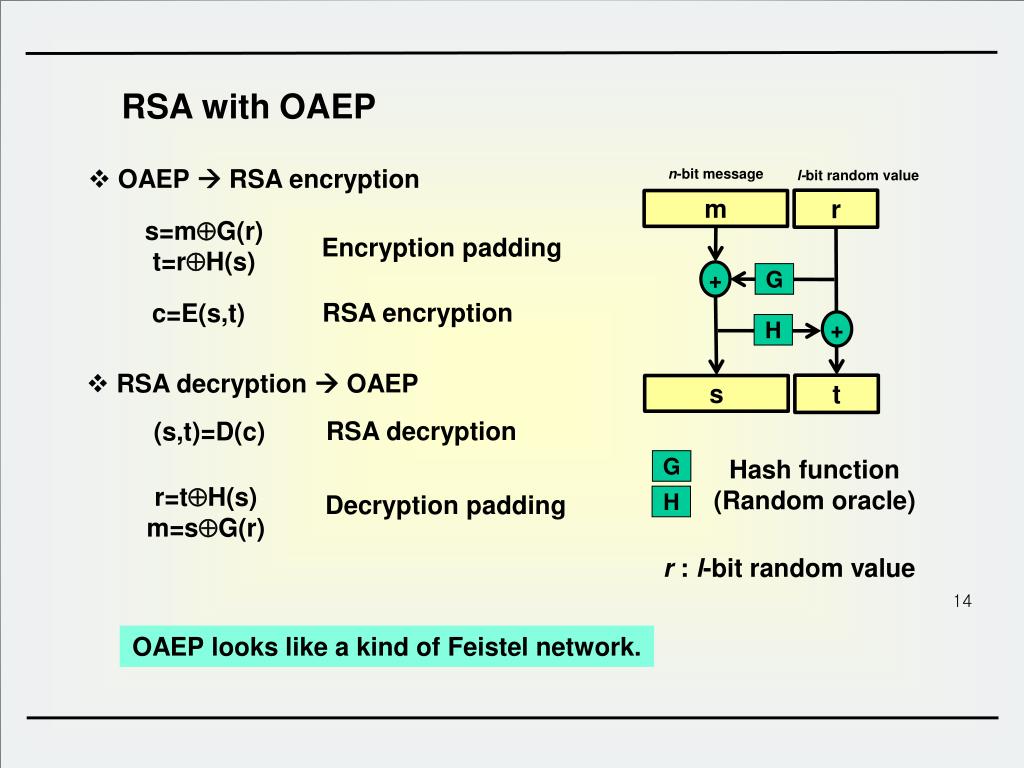
Действия объекта B:

• Расшифровывает принятую криптограмму C₁, C₂, C₃ используя секретный ключ ≡ = 3 по формуле:M_i = C_i^K_в (mod N) = C_i³ (mod 3)
  • M₁= 9³ (mod 33) = 729 (mod 33) =3.
  • M₂ = 1³ (mod 33) = 1 (mod 33) =1.
  • M₂ = 29³ (mod 33) = 24389 (mod 33) =2.

Объект получил исходное сообщение, которое послал объект A.

Шифрование с помощью RSA есть одним из методов защиты информации при передачи данных через сеть Интернет. Схема Рабина очень похожа на схему RSA. Криптоалгоритм RSA признан стойким при дине ключа больше 1024 бит. Нужно отметить что алгоритм применяют как для шифрования так и для электронно-цифровой подписи. Нетрудно заметить что в асимметричной криптосистеме RSA количество ключей связано с количеством пользователей линейной зависимостью (N пользователей используют 2 × N ключей), а не квадратичной как это используется в симметричных системах.

Применение алгоритма может решить некоторые угрозы информационной безопасности в сети.

Если сравнивать самые популярных представителей асимметричного и симметричного шифрования, нужно отметить, что по скорости RSA уступает DES, да и реализация криптоалгоритма RSA сложнее. Поэтому RSA обычно используется для передачи небольших сообщений. Шифрование как таковое, частично решает проблемы защиты информации в сетях.

• генерация псевдослучайных чисел.
• Длина криптографического ключа
• поточные шифры
• блочное шифрование

Оценка статьи:

Загрузка…

Поделиться с друзьями:

Пример RSA – Практическая работа в сети .net

Алгоритм RSA является наиболее широко используемым алгоритмом асимметричного шифрования, развернутым на сегодняшний день.

Аббревиатура образована от фамилий трех математиков, создавших ее в 1977 году: Рон Р Ивест, Ади С Хамир, Леонард А Длеман.

Чтобы понять алгоритм, мы должны определить несколько терминов:

• Простое число . Число называется простым, если оно делится только на 1 и само на себя. Например: 2, 3, 5, 7, 11, 13 и т. д.

• Коэффициент — Коэффициент — это число, которое можно умножить, чтобы получить другое число. Например, множители числа 12 равны 1, 2, 3, 4, 6 и 12.

• Semi-Prime — число является Semi-Prime, если только его делители являются простыми (за исключением 1 и самого себя). Например:
  12 — это , а не полупростое число — один из его делителей равен 6, что не является простым числом.
  21   — это полупростое число — множители 21 равны 1, 3 , 7 , 21.  Если мы исключим 1 и 21, у нас останутся 3 и 7, оба из которых являются простыми.
   (Подсказка: каждый раз, когда вы умножаете два простых числа, результат всегда полупростой)

• Модули — это причудливый способ просто запросить остаток. Если представить задачу 12 MOD 5 , мы просто спрашиваем остаток при делении 12 на 5, в результате чего получается 2.

После этого мы можем перейти к самому алгоритму.

 

Генерация ключа RSA

Суть асимметричного шифрования заключается в поиске двух математически связанных значений, которые могут служить открытым и закрытым ключами. Таким образом, основная часть работы заключается в генерации таких ключей.

Чтобы получить такие ключи, выполните пять шагов:

1. Выберите два простых числа: P и Q

Это действительно так просто, как кажется. Выберите два простых числа, чтобы начать генерацию ключа. В нашем примере мы будем использовать числа 9.0005 7 и 19 , и мы будем называть их P и Q .

2. Рассчитать произведение: (P*Q)

Затем мы просто перемножаем наши два простых числа, чтобы вычислить произведение:

7 * 19 = 133

Мы будем называть это число N . Дополнительный вопрос: учитывая терминологию, которую мы рассмотрели выше, что за число такое N?

3. Вычислить общую сумму N: (P-1)*(Q-1)

При определении и приобретении Totient требуется много умной математики. Большинство из которых выходит за рамки предполагаемой области этой статьи. Итак, пока мы просто примем, что формула для получения Тотиента для полупростого числа состоит в вычислении произведения единицы, вычтенной из каждого из двух его простых множителей. Или, проще говоря, чтобы вычислить Totient полупростого числа, вычислите P-1, умноженное на Q-1.

Применительно к нашему примеру мы рассчитали бы:

(7-1)*(19-1) = 6 * 18 = 108

Далее мы будем называть это T .

4. Выберите открытый ключ

Открытый ключ — это значение, которое должно соответствовать трем требованиям:

• Он должен быть простым
• Должно быть меньше Totient
• Это НЕ должно быть фактором Totient

Давайте посмотрим, сможем ли мы обойтись числом 3:  3 действительно простое число, 3 действительно меньше 108, но, к сожалению, 3 является множителем 108, поэтому мы не можем его использовать. Можете ли вы найти другой номер, который будет работать? Вот подсказка, есть несколько значений, удовлетворяющих всем трем требованиям.

Для нашего примера мы выберем 29 в качестве нашего открытого ключа и будем называть его E в дальнейшем.

5. Выберите закрытый ключ

Наконец, с учетом того, что мы уже подсчитали, мы можем выбрать наш закрытый ключ (который мы назовем D ). Закрытый ключ должен соответствовать только одному требованию: произведение открытого ключа и закрытого ключа. при делении на Тотиент должен давать в остатке 1. Или, проще говоря, должна быть верна следующая формула:

(D*E) MOD T = 1

Есть несколько значений, которые также подходят для закрытого ключа. Но опять же, для нашего примера мы выберем 41 . Чтобы проверить это по нашей формуле, мы могли бы вычислить:

(41 * 29) MOD 108

Мы можем использовать калькулятор, чтобы проверить, действительно ли результат равен 1. Это означает, что 41 будет работать. как наш закрытый ключ.

Вот и все, мы прошли каждый из этих пяти шагов и получили следующие значения:

Теперь мы просто выбираем значение, которое будет использоваться в качестве нашего открытого сообщения, и мы можем увидеть, действительно ли асимметричное шифрование работает так, как они говорят.

В нашем примере мы будем использовать 99  в качестве открытого текста.

(на этом этапе математика становится довольно большой, если вы пытаетесь следовать, я предлагаю использовать утилиту Linux Bash Calculator)

Шифрование сообщений

Используя ключи, которые мы сгенерировали в приведенном выше примере, мы запускаем через процесс шифрования. Напомним, что при асимметричном шифровании мы шифруем с помощью открытого ключа, а расшифровываем с помощью закрытого ключа. 929 MOD 133 = 92

Результатом 92 является наш зашифрованный текст. Это значение, которое будет отправлено по сети, и только владелец коррелирующего закрытого ключа сможет расшифровать и извлечь исходное сообщение. У нас была пара ключей 29 (публичный) и 41 (закрытый). Итак, давайте посмотрим, действительно ли мы можем извлечь исходное сообщение, используя наш закрытый ключ:

Формула для расшифровки с помощью ключей RSA: Оригинал M essage = 941 MOD 133 = 99

В качестве эксперимента попробуйте подставить открытый ключ (29) в формулу расшифровки и посмотрите, принесет ли это вам что-нибудь полезное. Вы заметите, что, как было сказано ранее, невозможно использовать один и тот же ключ для шифрования и расшифровки.

Подписание сообщений

Но помните, это не все, что мы можем сделать с парой ключей. Мы также можем использовать ту же пару ключей в обратном порядке для проверки подписи сообщения.

Для этого мы будем использовать те же формулы, что и выше, за исключением того, что на этот раз мы будем уважать использование открытого и закрытого ключа. Мы собираемся зашифровать с помощью закрытого ключа и посмотреть, сможем ли мы расшифровать с помощью открытого ключа. 929 MOD 133 = 99

---

 

Вот и все. Полностью рабочий пример возможностей генерации ключей RSA, шифрования и подписи.

Здесь следует отметить, что то, что вы видите выше, считается «ванильным» RSA. При промышленном использовании шифрования RSA используемые числа на значительно больше на . Фактически, современная передовая практика RSA заключается в использовании размера ключа 2048 бит. Это коррелирует со значением N в нашем расчете выше. Два простых числа, используемые в современном RSA, должны давать произведение, равное 2048 битам.

И просто чтобы дать вам представление о том, насколько велико 2048-битное число. Ранее мы видели, что 128-битное число можно записать в десятичном виде с помощью 39 цифр. 2048-битный ключ экспоненциально длиннее — для полной записи потребуется примерно 617 цифр.

---

Предпочитаете видеоконтент тексту? Большая часть этой статьи была записана и может быть просмотрена на Youtube:

Series NavigationAnti-Replay >>Diffie-Hellman >>

RSA

RSA

В 1978 году Ривест, Шамир и Адлеман из Массачусетского технологического института предложили теоретико-числовой способ реализации криптосистемы с открытым ключом. Их метод получил широкое распространение. Базовая техника:

• Выберите два больших простых числа. номера, р и q .
• вычислить n = p * q и x = ( p -1)*( q -1)
• Выберите число относительно простое число x и назовите его d . Это означает, что д не является простым множителем числа x или кратное ему.
• Найдите e такие, что e  *  d  = 1 mod  x .

Чтобы использовать этот метод, разделите открытый текст (рассматриваемый как битовая строка) на блоков так, чтобы каждое открытое текстовое сообщение P попадает в интервал 0 <=  P  <  n . Это можно сделать, разделив его на блоки по k бит, где k — это наибольшее целое число, для которого 2 k  <  n правда.

Для шифрования: C  =  P e  (mod  n )
Для расшифровки: P 0054  =  C d  (mod  n )

Открытый ключ, используемый для шифрования, имеет следующий вид: ( e , n ) и закрытый ключ, используемый для расшифровки: ( d , n ) )

 

Пример RSA — генерация ключа

Чтобы создать открытый ключ, выберите два больших положительных простых числа. номера р и q	p  = 7,  q  = 17 Достаточно большой для нас!
Вычислить ( p -1) * ( q -1)	x  = 96
Выберите целое число E что относительно просто x	E  = 5
Вычислить n  =  p  *  q	n  = 119
К р тогда n в сочетании с E	К р  = 119, 5

 

Чтобы создать секретный ключ, вычислите D так, чтобы ( D  *  E ) mod  x  = 1

К с  = 119, 77

Пример RSA — шифрование и дешифрование

Чтобы вычислить зашифрованный текст C открытого текста P , обработайте P как числовое значение	P  = 19
C = P E мод n	С  = 66

 

Для вычисления открытого текста P из зашифрованного текста C :
P = C D мод n	P  = 19

RSA на практике

RSA работает, потому что знание открытого ключа не раскрыть закрытый ключ. Обратите внимание, что и открытый, и закрытый ключи содержат важное число n = p * q . Безопасность системы основана на том факте, что n трудно разложить на множители — то есть при большом числе (даже таком, о котором известно, что основные факторы) нет простого способа узнать, что они из себя представляют. это колодец известный математический факт. Если быстрый метод факторизации равен когда-либо обнаружен, то RSA перестанет быть полезным.

Это это очевидно возможно взломать RSA с помощью скотина атака force — просто разложите n . Чтобы сделать это трудным, это обычно рекомендуется выбирать p и q так, чтобы n было (в номера 2002 года) не менее 1024 бит.

Одной из превосходной особенностью RSA является то, что он симметричен . Мы уже знаем, что если вы зашифруете сообщение моим открытым ключом, то только я может расшифровать этот зашифрованный текст, используя мой секретный ключ. Однако оказывается также что сообщение зашифровано моим секретным ключом можно расшифровать только с помощью мой открытый ключ . Это имеет важные последствия, см. далее.

Алгоритм RSA работает с огромными числами и включает множество возведение в степень (т. е. многократное умножение) и арифметика по модулю. Такой операции вычислительно затратны (т.е. они занимают много времени время!) и поэтому шифрование и дешифрование RSA невероятно медленно , даже на быстрых компьютерах. Сравните это с операции, связанные с DES (и другие одноклавишные системы) которые состоят из повторяющихся простых XOR s и транспозиций. Типичные цифры таковы, что DES в 100 раз быстрее, чем RSA. на эквивалентном оборудовании. Кроме того, DES может быть легко реализован в выделенном аппаратное обеспечение (RSA, вообще говоря, является программной технологией), дающее повышение скорости до 10000 раз.