8-900-374-94-44
LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд
напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной.
И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и
электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
И начнём мы с расчёта самого простого LC-фильтра — колебательного контура.
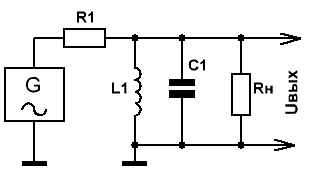
Включённый по приведённой на рис.1 схеме, он представляет собой узкополосный полосовой фильтр, настроенный на частоту
fо= 1/2π√LС.
Рис.1
На низких (звуковых) частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить тестером. Если эта попытка удалась, то Q=2πfL/R, где R – активное сопротивление катушки индуктивности.
На радиочастотах значение активного сопротивления катушки может составлять доли ома, поэтому для расчёта добротности надо — либо
найти сопротивление в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в
метрах, d — диаметр провода в мм, либо вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким
внутренним сопротивлением, и определить добротность экспериментально.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 200 омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядок меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).
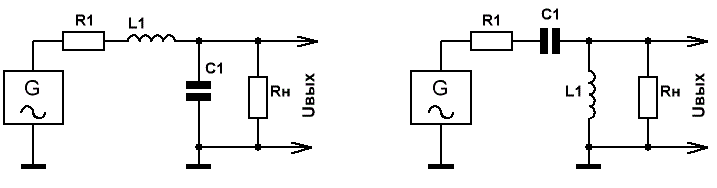
Рис.2
Крутизна спада АЧХ этих фильтров в полосе подавления — 12 дБ/октаву, коэффициент передачи в полосе пропускания К=1 при R1
Однако наилучшие параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются
при R1=Rн=ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Данные ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.
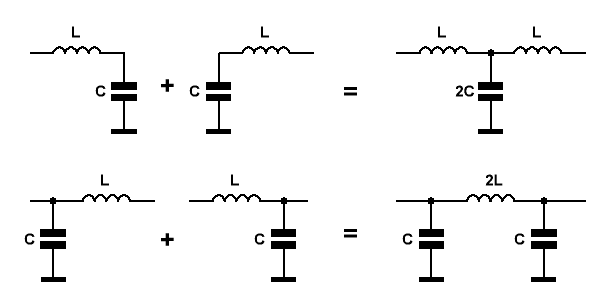
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками.
Широкополосные полосовые LC — фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.
Полосовой, он же полосно-пропускающий фильтр — это фильтр, пропускающий частоты в некоторой полосе частот,
находящейся между нижней и верхней частотами среза, и может быть легко представлен в виде последовательности,
состоящей из фильтра нижних частот и фильтра верхних частот.
Однако более рациональными с точки зрения оптимизации характеристик, являются фильтры, рассчитанные через ФНЧ-прототип.
Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами,
а индуктивностей — последовательными.
Примеры таких полосовых фильтров 3-го, 5-го и 7-го порядков приведены на Рис.1.
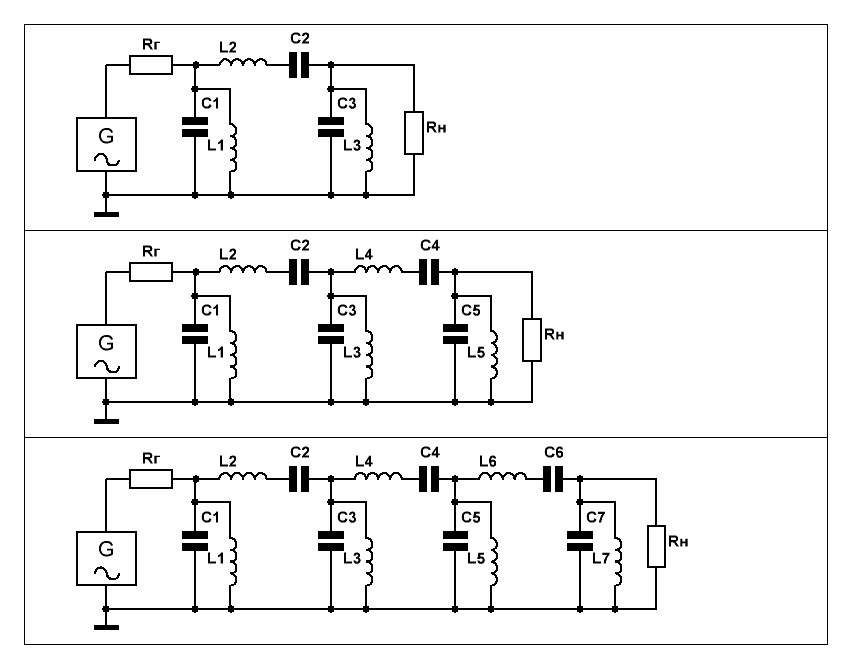
Рис.1
Расчёт поведём, используя прототипы фильтров нижних частот имени уважаемого Пафнутия Чебышева и таблицы не менее уважаемого господина Гранта Ханзела, приведённые в справочнике по расчёту фильтров.
ТАБЛИЦА РАСЧЁТА ПОЛОСОВЫХ LC ФИЛЬТРОВ.
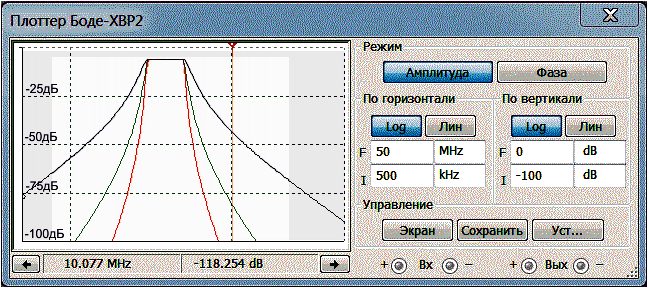
Рис.2
Характеристики затухания фильтров вне полосы пропускания симметричны и составляют величины: 38 дБ на октаву для фильтров 3-го порядка, 75 дБ — для фильтров 5-го порядка и 112 дБ — для фильтров 7-го порядка. Неравномерность в полосе пропускания — менее 0,5 дБ.
Приведённая таблица может стать хорошим подспорьем при расчёте входных диапазонных фильтров радиоприёмников и трансиверов,
однако следует учитывать маленький, но ЖИРНЫЙ «НЮАНС»:
Фильтры Чебышева значительно лучше других справляются с подавлением внеполосных сигналов, но становятся
крайне неудобными (с точки зрения критически малых значений номиналов некоторых элементов) при выборе узкой полосы
прозрачности.
А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня
на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания?
А как насчёт расчёта активных полиномиальных фильтров второго порядка на
звеньях Рауха, Сален-Ки и биквадратного звена?
«Хватит умничать, пальцем покажи!», — предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы.
И действительно. Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать!
Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.
Определимся с терминологией.
— Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы
высоких частот.
— Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
— Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.
А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).
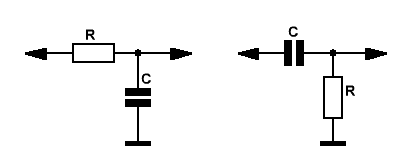
Рис.1
Крутизна спада АЧХ таких фильтров в полосе подавления — 6 дБ/октаву.
Частота среза рассчитывается по формуле:  
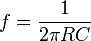
Теперь надо определиться — из каких соображений выбирать номиналы R и С.
Ёмкость посчитается нашей табличкой, а к выбору сопротивления резистора, для достижения заявленной крутизны, надо подойти со всей
ответственностью.
Номинал этого резистора должен быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.
РИСУЕМ ТАБЛИЧКУ ДЛЯ ФИЛЬТРОВ ПЕРВОГО ПОРЯДКА
ТЕПЕРЬ ТО ЖЕ САМОЕ С ДРУГИМИ ВВОДНЫМИ
Важно понимать, что хорошей крутизны спада АЧХ от таких простейших фильтров добиться не удастся. Тут нам прямая дорога к активным фильтрам, или к фильтрам на LC цепях.
Именно активные фильтры мы и рассмотрим на следующей странице.
И начнём мы с активных фильтров нижних частот (ФНЧ) и фильтров верхних частот (ФВЧ) 2-го и 3-го порядков имени товарищей Бесселя, Баттерворта и Пафнутия нашего Чебышева.
Эко нас понесло! Почему бы не удовлетвориться одним учёным мужем? К примеру, привычный с детства Баттерворт совсем не плох, к тому же широко известен в узких кругах.
Согласен, с какой стороны не возьми, Баттерворт — хорошая штука. Тут тебе и максимально гладкая АЧХ на частотах полосы пропускания, и
приличный спад характеристики в полосе подавления, однако…
Если на первый план выдвигается линейность фазо-частотной характеристики в полосе пропускания фильтра (например, в аудио-кроссоверах),
то пальма первенства в АЧХ-строении переходит к обратному многочлену профессора Фридриха Вильгельма Бесселя, ну а если ФЧХ нам
до фени, а в приоритете максимально крутой спад характеристики на частотах полосы подавления, то как ни крути, придётся с головой
окунуться в полиномы Пафнутия Львовича Чебышёва.
Фильтры построим на основе повторителей, они просты в расчётах, к тому же легко могут быть реализованы не только на операционных усилителях, но и на транзисторах.
А желающим спроектировать активный фильтр нижних частот 3-6-го порядка с перестраиваемой частотой среза, следует посетить страницу ссылка на страницу .
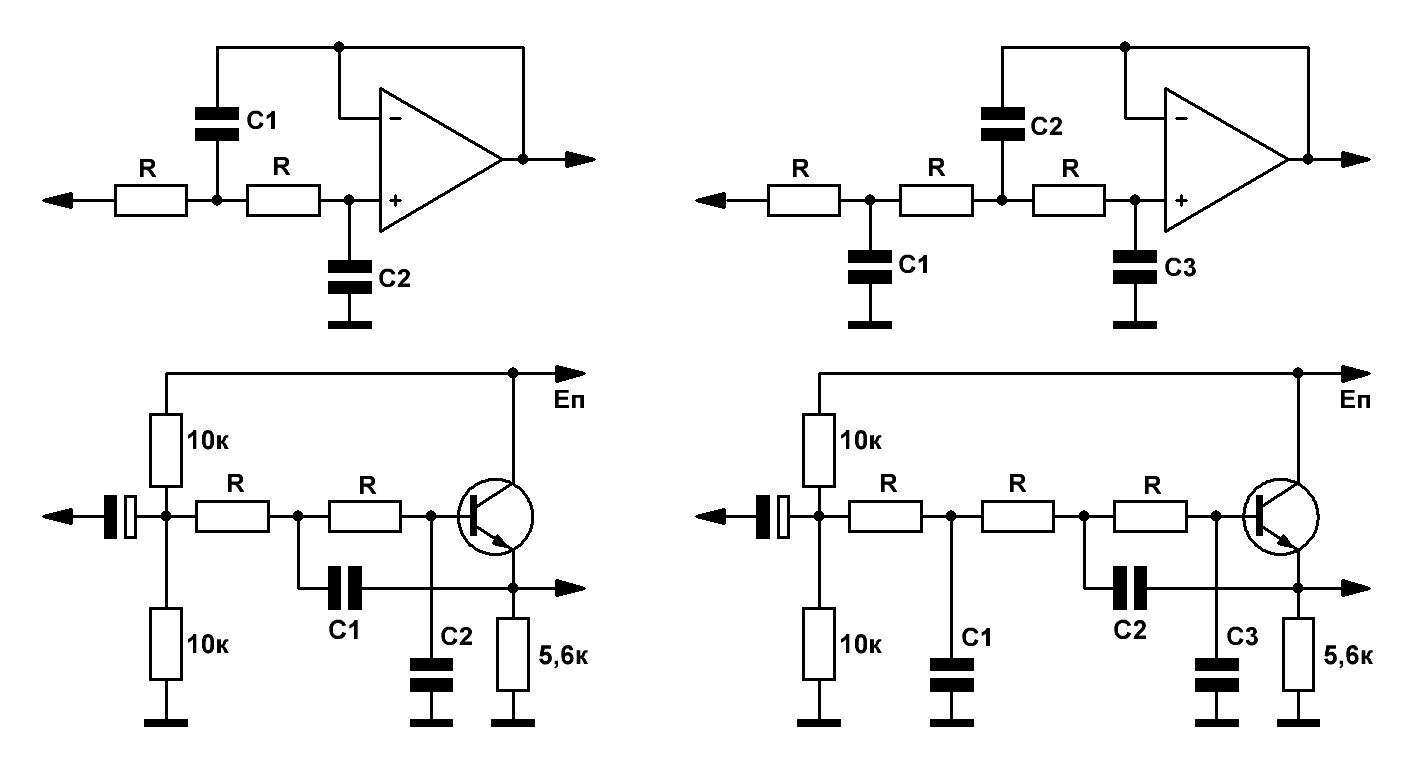
Рис.1
На Рис.1 приведены схемы активных фильтров нижних частот (ФНЧ) 2-го и 3-го порядка на ОУ и, для примера, реализация фильтра на биполярном транзисторе, отличающаяся от схем на операционниках только наличием двух резисторов, задающих необходимое напряжение смещения на базе.
Крутизна спада АЧХ этих фильтров в полосе подавления для Бесселя — около 5 дБ/октаву на каждый порядок фильтра, для
Баттерворта — 6 дБ/октаву и около 8 дБ/октаву для Чебышёва.
Коэффициент передачи в полосе пропускания К=1, а номиналы рассчитываются исходя из формул:
C1=КС1/(2π*F*R)   C2=КС2/(2π*F*R)   C3=КС3/(2π*F*R), где коэффициенты
КС1, КС2 и КС3 зависят как от порядка фильтра, так и от его принадлежности к той или иной фамилии.
К примеру для фильтров Баттерворта 2-го порядка КС1=1,114, КС2=0,707, а для фильтров Баттерворта 3-го порядка
КС1=1,393, КС2=3,549, КС3=0,202.
Критерии выбора величины сопротивления R, такие же, как и в пассивных фильтрах, она должна быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления ОУ или ЭП (на практике 1-100 кОм).
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНЫХ ФНЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
Плавно переходим к активным фильтрам верхних частот (ФВЧ) 2-го и 3-го порядка на ОУ (Рис.2). В транзисторной реализации резисторы, задающие напряжение смещения на базе, уже участвуют в формировании необходимой АЧХ фильтра, поэтому значение Rб1 ll Rб2 должно равняться значению резистора R2 в ФВЧ 2-го порядка, либо R3 в ФВЧ 3-го порядка.
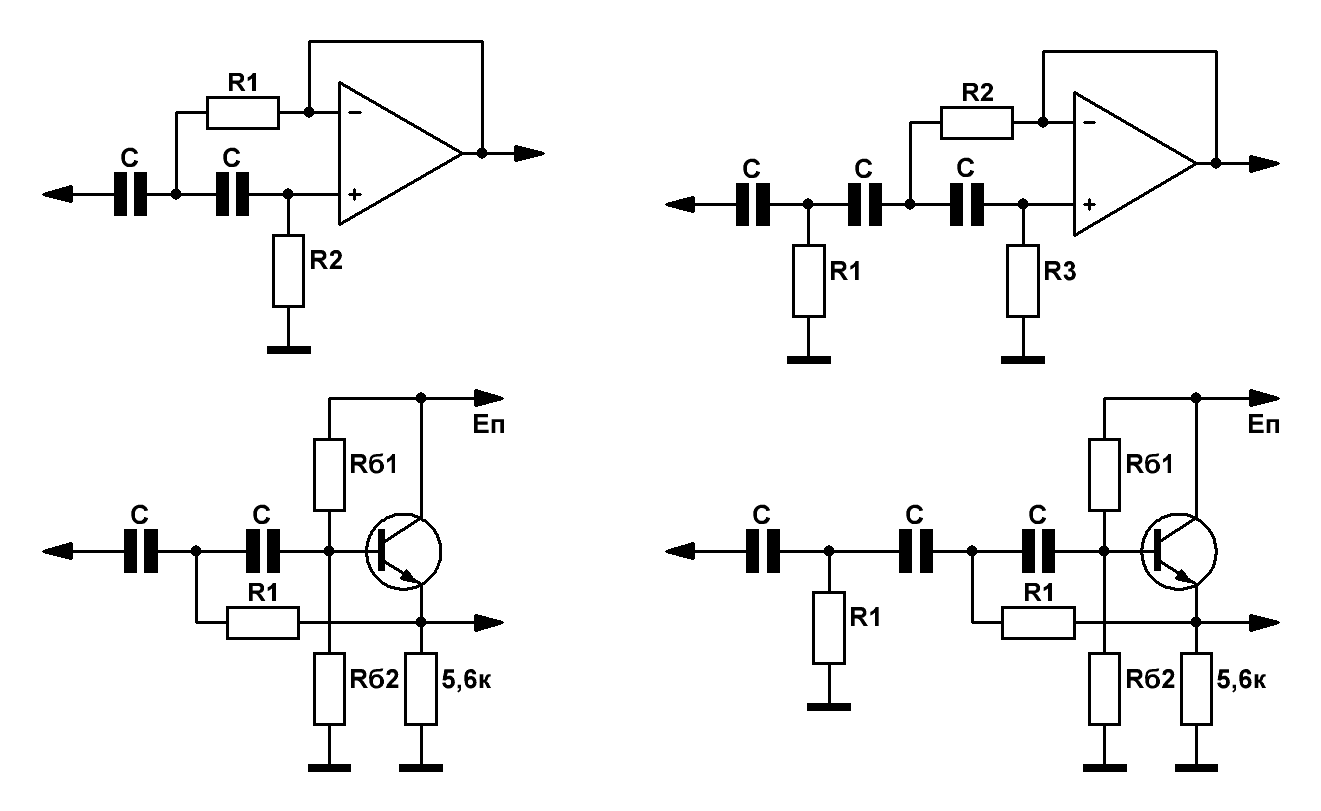
Рис.2
Номиналы элементов рассчитываются исходя из следующих формул:
R1=КR1/(2π*F*C) R2=КR2/(2π*F*C) R3=КR3/(2π*F*C)
Rrб1llRrб2=R2 для фильтров 2-го порядка, либо Rrб1llRrб2=R3 для 3-го.
Для фильтров Баттерворта 2-го порядка КR1=0,707, КR2=1,414, а для фильтров Баттерворта 3-го порядка
КR1=0,717, КR2=0,282, КR3=4,950.
И опять же, изначально надо определиться с номиналом R1, исходя из принципов, описанных в предыдущих схемах.
ТАБЛИЦА ДЛЯ РАСЧЁТА АКТИВНЫХ ФВЧ БЕССЕЛЯ, БАТТЕРВОРТА И ЧЕБЫШЕВА
И наконец, мы подобрались к схеме полосового активного фильтра.
Здесь всё несколько сложнее, поскольку, при расчёте фильтра, помимо значения центральной частоты, нам не стоит забывать
и про такие немаловажные вещи, как коэффициент передачи фильтра в полосе пропускания, да и собственно ширину самой полосы
пропускания.
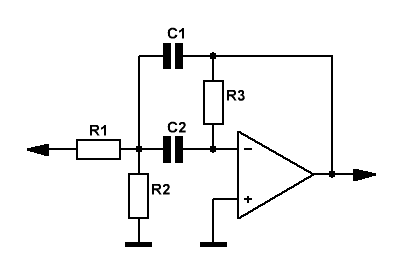Формулы, для расчёта элементов:
C1=C2=C
R1=Q/(2πF*Kп*C)
R2=Q/((2πF*C*(2Q²-Kп))
R3=2Q/(2πF*C)
Q=F/Bпр, где
Q-добротность фильтра,
Впр-полоса пропускания по уровню -3дБ,
F-центральная частота фильтра,
Кп-коэффициент передачи фильтра в полосе пропускания.
Рис.3
В фильтре, приведённом на рисунке, не стоит слишком усердствовать с высокими значениями добротности и коэффициента передачи. Как показывает практика, и тот и другой параметр следует ограничить сверху на уровне 5-6 единиц.
Как всегда, начинаем с выбора номинала резистора R1, который как минимум в 10 раз должен быть выше выходного импеданса предыдущего каскада.
РИСУЕМ ТАБЛИЦУ ДЛЯ АКТИВНОГО ПЛОСОВОГО ФИЛЬТРА 2-го ПОРЯДКА
А что делать, если полученные значения элементов не попадают в стандартную сетку?
Не беда, нарисуем ещё одну таблицу, но до этого надо поиграться коэффициентом передачи фильтра в небольших пределах (например,
сделать не 1,5, а 1,45, или 1,55) до достижения значения R3 величины, попадающей в сетку. Номинал R1 мы уже выбрали, исходя из соображений
приемлемого входного импеданса.
Предположим, нам надо рассчитать фильтры для 10-полосного эквалайзера.
Фильтры у нас получаются октавные, стандартное значение добротности для них Q=1,41.
R1 выберем номиналом 30кОм, Кпер = 1,5. Произведём расчёт для частоты 1000 Гц.
Подставив эти цифры в верхнюю таблицу, получаем С=4987пФ, R2=18,173кОм, R3=90кОм.
Пошебуршав туда-сюда Кпер, понимаем, что для получения стандартного значения R3=91кОм, коэффициент передачи фильтра должен
быть равен 1,517, что для нашего случая вообще не принципиально, тем более, что это значение Кпер будет сопровождать все фильтры,
независимо от частоты.
Итак, подставляем в нижнюю таблицу R1=30кОм, R3=91кОм, R2=18кОм, стандартное значение ёмкости С=5100пФ и естественным образом
видим, что значение резонансной частоты у нас съехало до 975Гц.
Но у нас было с собой, а именно замечательное сопротивление R2, которое никак не влияет на Кпер, и весьма скромно — на добротность.
Покрутив номинал этого резистора, получаем — 16,7кОм, центральную частоту — 999Гц и добротность — 1.46. Всё, расчёт фильтра — завершён.
ЕЩЁ ТАБЛИЦА ДЛЯ АКТИВНОГО ПОЛОСОВОГО ФИЛЬТРА
Для желающих рассчитать параметры и элементы многополосных графических эквалайзеров следует посетить страницу ссылка на страницу , а на следующей странице мы рассмотрим универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.
Одиночный LC-фильтр, как ни бейся, не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для
формирования более крутой переходной области обычно используют многозвенные LC — фильтры.
Причём фильтры чётных порядков при равенстве сопротивлений источника и нагрузки вообще теряют актуальность, ведь добавлением всего
одного конденсатора они превращаются в фильтр более высокого порядка.
В низкочастотной схемотехнике LC-фильтры фильтры решительно теряют позиции в пользу активных фильтров высоких порядков, за исключением, пожалуй, сглаживающих фильтров источников питания, LC-фильтров акустических систем, да изредка НЧ фильтров приёмников прямого преобразования.
Зато на непаханых полях радиочастотных диапазонов свободного пространства хоть отбавляй. То-то раздолье тут земледельцу!
По левую руку — входные фильтры приёмников и трансиверов, по правую — фильтры выходных каскадов передатчиков, посередине …
А что, собственно говоря, посередине?
Да всё, что угодно, поля-то — непаханые.
Описания свободных и вынужденных колебаний в электрических цепях, и иже с ними дисперсионные и характеристические уравнения систем различных аппроксимаций оставим бедолагам студентам, а сами играючи воспользуемся таблицами элементов LC фильтров-прототипов, приведённых в справочнике по расчёту фильтров Г. Ханзела.
Как правило, с точки зрения минимизации количества катушек индуктивности, в многозвенных фильтрах используют П-образную схему для ФНЧ и Т-образную для ФВЧ.
На Рис.1 приведены схемы подобных фильтров нижних и верхних частот 3-го, 5-го и 7-го порядков.
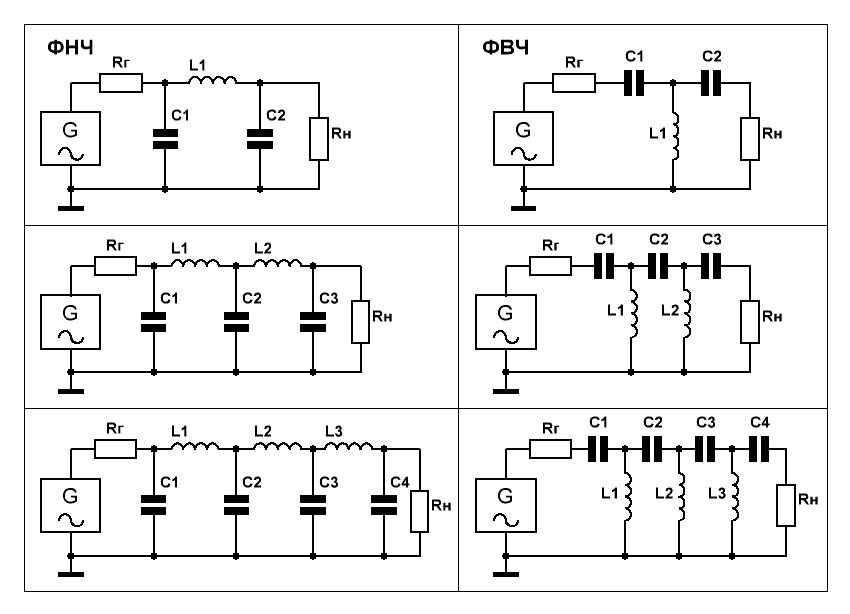
Рис.1
Расчёт поведём доверившись многочленам Пафнутия Львовича нашего Чебышёва.
Почему на сей раз Чебышева, а не вездесущего Баттерворта?
Ответ не сложен — в погоне за максимальным наклоном переходного участка, в жертву некоторой неравномерности АЧХ фильтра в полосе пропускания.
При одном и том же числе элементов схемы у фильтров Чебышева крутизна характеристики ослабления в полосе задерживания
значительно больше, чем у фильтров Баттерворта и может составлять величину 8,5дб на октаву (против менее 6 дБ/окт) на каждый порядок
фильтра.
Значение же неравномерности в полосе пропускания можно ограничивать, выбирая коэффициенты из таблицы фильтра — прототипа. Я посчитал, что
неравномерность 0,28дБ окажется вполне приемлемой.
Ну и хватит, переходим к таблице.
ТАБЛИЦА РАСЧЁТА МНОГОЗВЕННЫХ ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
И как обычно не забываем — многозвенные полосовые LC-фильтры получаются каскадным соединением ФНЧ и ФВЧ, тем более что они отлично друг с другом согласуются.
Ну а если полученный спад амплитудной характеристики не кажется слишком крутым, то нам прямая дорога к эллиптическим фильтрам, которые мы и посчитаем на следующей странице.
Что такое режекторный фильтр (он же полосно-заграждающий, он же — фильтр-пробка) и с чем его едят, мы определились на предыдущей странице, рассматривая пассивные и активные режекторные RC-фильтры.
Так же, как и в случаях с НЧ, ВЧ и полосовыми собратьями, LC режекторные фильтры обладают рядом достоинств, таких как: высокая стабильность, низкий уровень собственных шумов, а также возможность работы с широким спектром сигналов, включая СВЧ диапазоны.
Простейший представитель режекторного LC-фильтра 2-го порядка представлен на Рис.1.
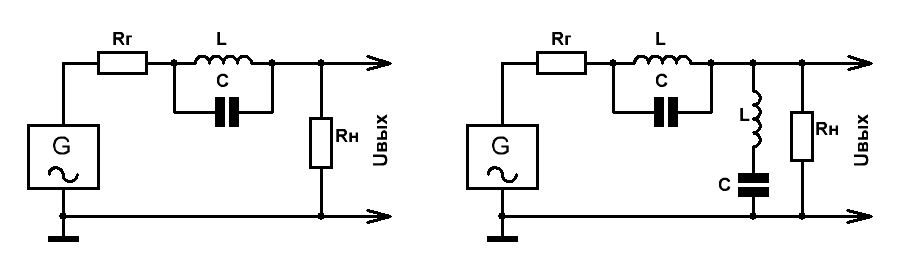
Рис.1 
Рис.2
Логика работы такого фильтра предельно проста.
На резонансной частоте fо= 1/2π√LС сопротивление параллельного
колебательного контура, образованного катушкой индуктивности L и конденсатором C, принимает максимальное значение, соответственно
максимальное значение принимает и коэффициент подавления сигнала на этой частоте.
Глубина режекции (подавления частоты fo) этого фильтра при работе на согласованную нагрузку, равную характеристическому сопротивлению
колебательного контура ρ = √L/C , достигает 45 дБ.
На Рис.2 представлена схема Г-образного режекторного фильтра 4-го порядка.
Принцип работы этого фильтра основан на использовании резонансов напряжений и токов в последовательных и параллельных
колебательных контурах.
На частоте резонанса сопротивление параллельного плеча оказывается максимальным, а последовательного – минимальным, что и
соответствует наибольшему затуханию цепи.
Глубина режекции в данной схеме уже может составлять величину 90 дБ.
Приведём таблицу для расчёта элементов этих фильтров.
Не забываем, что характеристическое сопротивление фильтра ρ
должно равняться Rг =Rн.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ LC- ФИЛЬТРОВ 2-го и 4-го ПОРЯДКОВ
Для получения больших значений подавления центральной частоты (глубины режекции) используют два или более Г-образных звеньев,
соединяя их последовательно, чтобы образовать Т-образное звено, или П-образное звено.
На Рис.3 приведены схемы типовых полосно-заграждающих LC-фильтров 6-го порядка Т-образной (слева) и П-образной (справа) структур с
глубиной режекции — около 130 дБ.
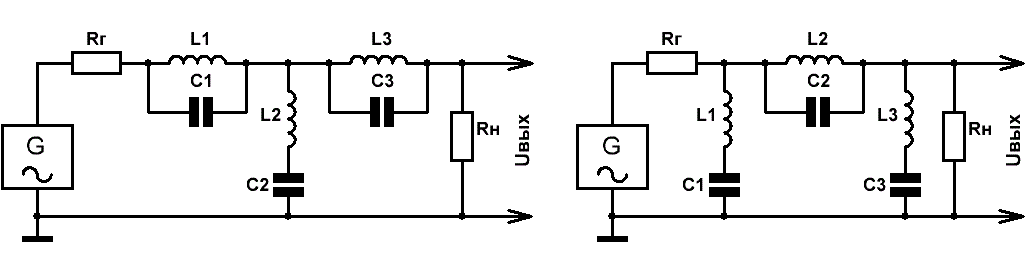
Рис.3
Ничего не изменилось — последовательная ветвь обладает минимальным полным сопротивлением и оказывает шунтирующее воздействие на
центральной частоте диапазона.
Ее полное сопротивление начинает увеличиваться по обе стороны от частоты резонанса.
Параллельная же ветвь на центральной частоте имеет максимальное сопротивление, и оно уменьшается по обе стороны резонанса.
Центральная частота режекции равна fо= 1/2π√LС,
характеристическое сопротивление ρ = √L/C ,
а значения частотозадающих элементов рассчитываются исходя из следующих равенств:
L1 = L3 = L/2, L2 = L, C1 = C3 = C×2, C2 = C
для Т-образного фильтра,
L1 = L3 = L×2, L2 = L, C1 = C3 = C/2, C2 = C
для П-образного фильтра.
Приведём таблицу для расчёта элементов и этих фильтров.
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ Т- и П-образных LC- ФИЛЬТРОВ
Ширина полосы задержания представленных режекторных LC-фильтров составляет величину, примерно равную 50% от значения центральной частоты fo.
В конце предыдущей страницы мы определились, что если крутизна спада амплитудной характеристики линейных фильтров показала себя недостаточно «круто», то прямая широкая дорога у нас лежит к эллиптическим фильтрам, называемых фильтрами Кауэра по имени немецкого деятеля наук Вильгельма Кауэра, описавшего их замечательные свойства.
Фильтры эти отличаются от классических линейных аналогов наличием дополнительных конденсаторов, включённых параллельно в ФНЧ (или последовательно в ФВЧ) катушкам индуктивности.
Если рассуждать «на пальцах» — конденсаторы эти совместно с катушками образуют режекторные фильтры, частоты которых располагаются в непосредственной близости за пределами полосы пропускания. Они-то, собственно говоря, и формируют дополнительную крутизну спада АЧХ эллиптических фильтров.
На Рис.1 приведены схемы эллиптических фильтров Кауэра нижних и верхних частот 3-го, 5-го и 7-го порядков.
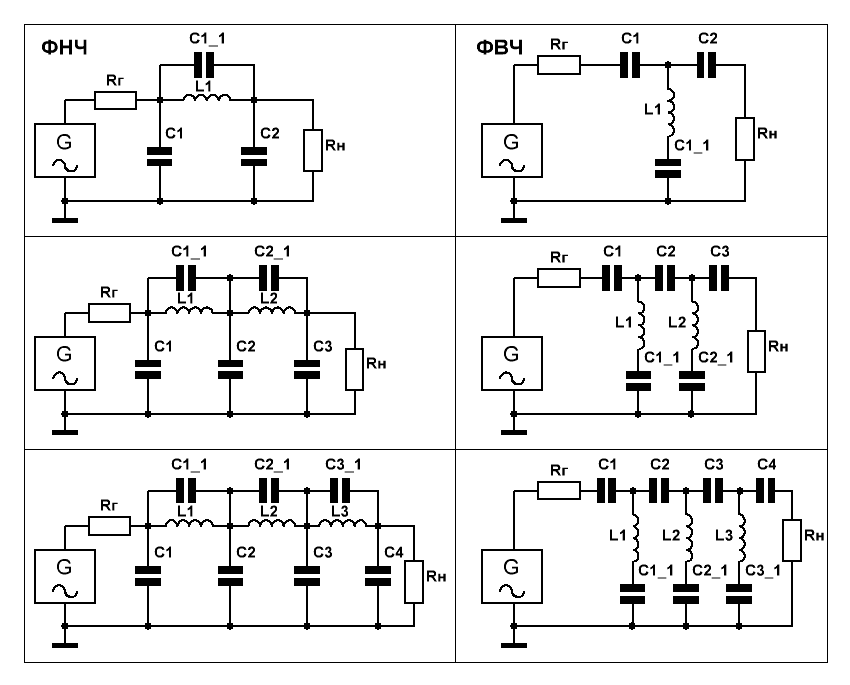
Рис.1
Эллиптические фильтры объединяют в себе свойства фильтров Чебышева первого и второго рода, поскольку АЧХ эллиптического фильтра имеет пульсации заданной величины, как в полосе пропускания, так и в полосе задерживания. За счёт этого удаётся обеспечить максимально возможную (при фиксированном порядке фильтра) крутизну ската АЧХ.
АЧХ фильтра описывается следующими параметрами: – частотой среза, – порядком фильтра, – параметрами, определяющие величины пульсаций в полосах пропускания и задерживания.
И снова, задавшись неравномерностью в полосе пропускания — менее 0,5дБ, мы доверимся одной из многочисленных таблиц уважаемого господина Ханзела, приведённых в справочнике по расчёту фильтров в далёком 1969 году.
ТАБЛИЦА РАСЧЁТА МНОГОЗВЕННЫХ ФИЛЬТРОВ КАУЭРА ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Для наглядности на Рис.2 приведены амплитудно-частотные характеристики двух вариантов фильтров нижних частот седьмого порядка,
с частотой среза 30МГц.
Синим цветом обозначена АЧХ фильтра Чебышева, описанного на предыдущей странице, красным — эллиптического фильтра Кауэра.
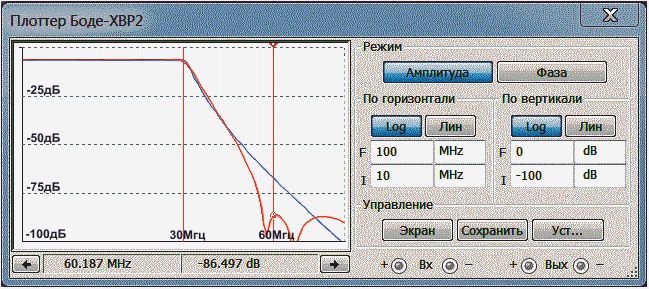
Рис.2
Для получения полосового фильтра — либо соединяем каскадно ФНЧ и ФВЧ, либо идём на следующую страницу и грамотно проектируем ПФ по умным таблицам из справочника.
90000 RF Wireless Vendors and Resources 90001 90002 About RF Wireless World 90003 90004 The 90005 RF Wireless World 90006 website is a home of RF and Wireless Vendors and Resources. The site covers articles, tutorials, vendors, terminology, source code (VHDL, Verilog, MATLAB, Labview), test and measurement, calculators, news, books, downloads and more. 90007 90004 The RF Wireless World site covers resources on various topics such as RF, wireless, vsat, satellite, radar, fiber optics, microwave, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, bluetooth, Lightwave RF, z-wave, Internet of Things (IoT), M2M, Ethernet etc.These resources are based on IEEE and 3GPP standards.It also has academic section which covers colleges and universities in engineering and MBA disciplines. 90007 90010 Articles on IoT based Systems 90011 90012 90004 90005 IoT based Fall detection system for elderly 90006: The article covers architecture of the Fall detection system used for elderly people. It mentions benefits or advantages of IoT Fall detection system. Read More➤ 90016 Also refer other articles on IoT based systems as follows: 90016 • AirCraft Lavatory Cleanliness System • Collision Impact Measuring System • Perishable Food and Vegetables Tracking System • Driver Assistance System • Smart Retail System • Water Quality monitoring System • Smart Grid System • Zigbee based Smart Lighting System • Zigbee based smart parking system • LoRaWAN based smart parking system 90007 90019 90010 RF Wireless Articles 90011 90004 This Articles section covers articles on Physical layer (PHY), MAC layer, protocol stack and network architecture based on WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit ethernet based IEEE / 3GPP etc .standards. It also covers test and measurement related articles on compliance testing used for device RF / PHY conformance tests. REFER ARTICLES INDEX >>. 90007 90019 90004 90005 5G NR physical layer 90006: The physical layer processing for 5G NR PDSCH channel and 5G NR PUSCH channel have been covered stepwise. This 5G physical layer description is as per 3GPP physical layer specifications. Read More➤ 90007 90019 90030 90004 90005 Repeater basics and repeater types 90006: It explains functions of different types of repeaters used in wireless technologies.Read More➤ 90007 90019 90004 90005 Fading basics and types 90006: This article covers small scale fading, large scale fading, slow fading, fast fading etc. used in wireless communication are explained. Read More➤ 90007 90019 90004 90005 5G Cell Phone architecture 90006: This article covers 5G Cell Phone Block diagram with internal modules of 5G Cellular phone architecture. Read More➤ 90007 90019 90046 90004 90005 Interference basics and Interference types: 90006 This article covers adjacent channel Interference, co-channel Interference, EM Interference, ICI, ISI, light Interference, Sound Interference etc.Read More➤ 90007 90019 90010 5G NR Section 90011 90004 This section covers 5G NR (New Radio) features, numerology, bands, architecture, deployment, protocol stack (PHY, MAC, RLC, PDCP, RRC) etc. 5G NR Quick reference Index >> 90016 • 5G NR Mini Slot • 5G NR Bandwidth Part • 5G NR CORESET • 5G NR DCI Formats • 5G NR UCI • 5G NR slot formats • 5G NR RRC IEs • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • 5G NR Reference Signals • 5G NR m-Sequence • 5G NR Gold Sequence • 5G NR Zadoff Chu Sequence • 5G NR Physical layer • 5G NR MAC layer • 5G NR RLC layer • 5G NR PDCP layer 90007 90019 90010 Wireless Technology tutorials 90011 90004 This section covers RF and Wireless tutorials.It covers tutorials on topics such as cellular communication, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, radar, VSAT, satellite, wlan, waveguide, antenna, femtocell, test and measurements, IoT etc. Refer TUTORIALS INDEX >> 90007 90019 90004 90005 5G tutorial 90006 -This 5G tutorial also covers following sub topics on the 5G technology: 90016 5G basics tutorial Frequency Bands millimeter wave tutorial 5G mm wave frame 5G mm wave channel sounding 4G Vs 5G 5G test equipments 5G network architecture 5G NR network interfaces channel sounding Channel types 5G FDD vs TDD 5G NR network slicing What is 5G NR 5G NR deployment modes What is 5G TF 90007 90019 90004 This 90005 GSM tutorial 90006 covers GSM basics, network architecture, network elements, system specifications, applications, GSM burst types, GSM frame structure or frame hierarchy, logical channels, physical channels, GSM physical layer or speech processing, GSM mobile phone network entry or call setup or Power ON procedure, MO call, MT call, VAMOS, AMR, MSK, GMSK modulation, physical layer, protocol stack, mobile phone basics, RF planning, PS call downlink and PS call uplink.90016 ➤Read more. 90007 90004 90005 LTE Tutorial 90006 covering LTE system architecture covering LTE EUTRAN and LTE Evolved Packet Core (EPC) basics. It provides link to LTE system overview, LTE air interface, LTE terminology, LTE UE categories, LTE frame structure, LTE physical layer, LTE protocol stack, LTE channels (logical, transport, physical), LTE throughput, LTE carrier aggregation, Voice Over LTE, LTE advanced, LTE vendors and LTE vs LTE advanced.➤Read more. 90007 90019 90010 RF Technology Stuff 90011 90004 This page of RF wireless world covers step by step design of RF frequency converter with example of 70 MHz to C band RF UP converter for microstrip board using discrete RF components viz. Mixers, Local oscillator, MMICs, synthesizer, OCXO reference oscillator, attenuator pads. ➤Read more. 90016 ➤RF Transceiver Design & Development ➤RF Filter design ➤VSAT System ➤Types & basics of microstrip ➤Waveguide basics 90007 90019 90010 Test and Measurement Section 90011 90004 This section covers T & M resources, test and measurement equipments for testing DUTs based on WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE standards.Test and Measurement INDEX >> 90016 ➤PXI system for T & M. ➤Signal generation and analysis ➤PHY layer measurements ➤WiMAX device conformance test ➤Zigbee conformance test ➤LTE UE conformance test ➤TD-SCDMA conformance test 90007 90019 90010 Fiber Optic Technology 90011 90004 90005 Fiber optic component 90006 basics including detector, optical coupler, isolator, circulator, switches, amplifier, filter, equalizer, multiplexer, connectors, de-multiplexer etc.This components are used in fiber optic communication. Optical Components INDEX >> 90016 ➤Fiber optic communication tutorial ➤APS in SDH ➤SONET basics ➤SDH Frame structure ➤SONET vs SDH 90007 90019 90010 RF Wireless Vendors, Manufacturers 90011 90004 RF Wireless World site covers manufacturers and vendors of various Rf components, systems and subsystems for vivid applications, refer Vendors INDEX >>. 90007 90103 90004 RF Component vendors covering rf isolator, rf circulator, rf mixer, rf amplifier, rf adapter, rf connector, rf modulator, rf transceiver, PLL, VCO, synthesizer, Antenna, oscillator, power divider, power combiner, filter, attenuator, diplexer, duplexer, chip resistor, chip capacitor, chip inductor, coupler, EMC stuff, RF Design Software, dielectric material, diode etc.RF Components Vendors >> 90016 ➤LTE Base station ➤RF Circulator ➤RF Isolator ➤Crystal oscillator 90007 90019 90010 MATLAB, Labview, Embedded Source codes 90011 90004 The RF Wireless World’s source code section covers MATLAB, VHDL, VERILOG and LABVIEW Programming languages related codes. These codes are useful for beginners in these languages. REFER SOURCE CODE INDEX >> 90016 ➤3 to 8 decoder VHDL code ➤Scrambler descrambler MATLAB code ➤32 bit ALU Verilog code ➤T, D, JK, SR flipflop labview codes 90016 90007 90016 90010 * General public health information * 90011 90004 Do these five simple things to help stop coronavirus (COVID-19).90016 DO THE FIVE 90016 1. HANDS: Wash them often 90016 2. ELBOW: Cough into it 90016 3. FACE: Do not touch it 90016 4. FEET: Stay more than 3ft (1m) apart 90016 5. FEEL: Sick? Stay home 90016 90007 90016 90004 Use Contact Tracing Technology >>, Follow social distancing >> guidelines and install data surveillance system >> to save hundreds of lives. Use of Telemedicine concept has become very popular in countries such as USA and China to stop the spread of COVID-19 as it is contagious disease.90007 90019 90010 RF Wireless Calculators and converters 90011 90004 The calculators and converters section covers RF calculators, wireless calculators as well as unit converters. These covers wireless technologies such as GSM, UMTS, LTE, 5G NR etc. REFER CALCULATORS Index >>. 90016 ➤5G NR Throughput calculator ➤5G NR ARFCN vs frequency conversion ➤LoRa Data Rate Calculator ➤LTE EARFCN to Frequency conversion ➤Yagi Antenna Calculator ➤5G NR sampling time calculator 90007 90019 90010 IoT-Internet of Things Wireless Technologies 90011 90004 The section on IoT covers Internet of Things wireless technologies such as WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth Low Power (BLE), NFC, RFID, INSTEON, X10, KNX, ANT +, Wavenis, Dash7, HomePlug and more.It also covers IoT sensors, IoT components and IoT companies. 90016 Refer IoT main page >> and following links. 90016 ➤THREAD ➤EnOcean ➤LoRa tutorial ➤SIGFOX tutorial ➤WHDI ➤6LoWPAN ➤Zigbee RF4CE ➤NFC ➤Lonworks ➤CEBus ➤UPB 90007 90016 90016 90010 RELATED POSTS 90011 90016 90010 RF Wireless Tutorials 90011 90016 90016 90010 Different types of sensors 90011 90016 90154 Share this page 90155 90016 90154 Translate this page 90155 90016 .90000 Narrow Band-pass Filter Calculator | Online Narrow Band-pass Filter Calculator App / Software Converter — CalcTown 90001 90002 This CalcTown calculator calculates the center frequency, quality factor and bandwidth of a narrow band-pass filter. 90003 90002 The multiple feedback bandpass filter has a simple design, but it is difficult to calculate the values for a given set of parameters. These filters are useful for equalization, analysis and other tasks such as the Sound to Light converter, vocoder, etc.90003 90002 This type of active band pass design produces a «tuned» circuit based around a negative feedback active filter through resistor R3 and capacitor C2 giving it a high Q-factor (up to 25) amplitude response and steep roll-off on either side of its center frequency. Because the frequency response of the circuit is similar to a resonance circuit, this center frequency is referred to as the resonant frequency, ƒr. 90003 90008 Narrow Band-pass Filter Calculator 90009 Capacitance, C (C1 or C2) CALCULATERESET 90002 Click here to view image 90003 90002 Where, 90003 90002 C1, C2 (C) = Capacitors 90003 90002 R1, R2, R3 = Resistors 90003 90002 Q = Quality Factor of the filter 90003 90002 BW = Bandwith of the filter 90003 90002 f 90023 c 90024 = center frequency of the filter 90003 90002 Resonant Frequency Point 90003 90002 The actual shape of the frequency response curve for any passive or active band pass filter will depend upon the characteristics of the filter circuit with the curve above being defined as an «ideal» band pass response.An active band pass filter is a 2nd Order type filter because it has «two» reactive components (two capacitors) within its circuit design. 90003 90002 As a result of these two reactive components, the filter will have a peak response or Resonant Frequency (ƒr) at its «center frequency», ƒc. The center frequency is generally calculated as being the geometric mean of the two -3dB frequencies between the upper and the lower cut-off points. 90003 90002 The «Q» or Quality Factor 90003 90002 In a Band Pass Filter circuit, the overall width of the actual pass band between the upper and lower -3dB corner points of the filter determines the Quality Factor or Q-point of the circuit.This Q Factor is a measure of how «Selective» or «Un-selective» the band pass filter is towards a given spread of frequencies. The lower the value of the Q factor the wider is the bandwidth of the filter and consequently the higher the Q factor the narrower and more «selective» is the filter. 90003.90000 Dale’s Homemade Robots — Bandpass Filter Calculator 90001 90002 Bandpass Filter Calculator 90003 90004 These are parts value calculators I wrote to help design analog active bandpass filters. They are op-amp based filters and are most useful in the audio frequency range. These parts calculators are based on formulas and tables from the book «Electronic Filter Design Handbook» by Arthur B. Williams. 90005 90004 Bandpass filters pass a contiguous range of frequencies while attenuating those above and below the passband.The calculators compute parts values for 2, 4 and 6 pole multiple-feeback bandpass (MFBP) filters. Click here for a tutorial on Bandpass filters. 90005 90004 Paul Falsted has a great online interactive Java program to help visualize filter responses with different poles and response types. Use it to see how a particular filter will perform. 90005 90004 90011 Usage 90012 90005 90004 Select the desired filter type from the drop down menu. Butterworth is optimized for flat frequency response in the pass band.Chebyshev sacrifices flatness for a steeper roll off in the stop band. This version has 0.1 dB of passband ripple. Bessel filters sacrifice both flatness and roll off for linear phase in the pass band. 90005 90004 Select the desired value for the capacitors. All the capacitors in the circuit are identical and for best results should be 1% tolerance. For midrange audio frequencies 0.01 uF is a good starting point. Note: Narrow bandwidth filters require tighter component tolerances than wide band filters.2. 90005 90004 Click COMPUTE and read the resistor values. If the values are not optimum try a different capacitor value and try again. For best results use 1% tolerance resistors. 90005 90004 Also computed are the Q and center frequency of each section of the filter. If the Q is too high parts values will be very critical and the op-amp will require higher performance. Q values up to about 20 are reasonable. Above that may result in an unstable circuit. Note: The center frequency of each section can be adjusted by varying R2 (R5 or R8).Frequency goes up as resistance goes down. 90005 90004 More information about MFBP circuits can be found with the help of Google. The source code is here. Report bugs via my contact page. 90005 90004 90011 Op-Amps 90012 90005 90004 The circuits below assume classic dual supply op-amps that use plus and minus power such as the LM348. If you use a single supply op-amp (eg: LM324) you will need to connect the grounds (R2, R5, + op-amp inputs) to a virtual ground, usually half way between real ground and Vcc.One way to do this is connect two 1K resistors in series between Vcc and ground. Connect a 10uF capacitor from the junction of the two resistors to ground. The junction of the two resistors is a virtual ground at Vcc / 2. Click here for an example. It’s for a high pass filter but the principle is the same. 90005 90004 I like to use single supply quad cmos op-amps such as LMC660 or LMC6484 because of their rail to rail output swing and wide bandwidth. The dual version is LMC6032. 90005 90004 Hit Counter = 113294 90005 90038 90039 .90000 SCHOTT Filter Transmission Calculator 90001 90002 90003 Online transmission calculator for SCHOTT optical color glass filters 90004 90005 90006 90007 90006 Our online SCHOTT-filter calculator allows you to individually calculate and analyze the transmission curves of nearly all SCHOTT color glass filter materials, which makes it easy to find out the best optical color glass filter for your application. We provide this useful tool to you for free. 90007 90006 90007 90006 90007 90006 If you like this tool, we invite you to place a direct link to this calculator on your website.Please solely use this link to refer to our calculator, and please consider our terms & conditions for the use of our optical glass filter calculator directly below. 90007 90006 90007 90003 Terms & Conditions for the use of our SCHOTT-filter calculator: 90004 90006 We do not take over any guarantee or liability for any technical data, specifications, or result. In no case, we take over guarantee or liability for the correctness of the generated curves, data, or information or any damage which might result from the use of this calculator program.The use of this optical glass filter calculator takes place entirely and solely in any implication at your own risk. All raw filter data used for this calculation program were supplied to us by the SCHOTT AG with kind permission to be used in our online calculator. 90007 90006 This calculator program is protected by national and international copyright laws and might not be copied or commercially exploited without our written permission. You might use the calculated curves for your purposes, but the curves must remain unmodified.The origin of the curve must be identifiable by a direct link to our online calculator. All measurement data used for the calculation of the filter curves are the property of the SCHOTT AG. The utilization of the data in this filter curve calculation program takes place with the kind permission of the SCHOTT AG. We reserve the right to change any technical and non-technical data without notice. 90007 90006 90007 90006 © 1994 — 2020 Präzisions Glas & Optik GmbH 90007 .