8-900-374-94-44
Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор). Для того, чтобы разобраться в этом, мы проведем простейший опыт.
Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт
Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.
Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.
Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы
Подаем напряжение с блока питания на лампу и вуаля!
Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра .
Ровнехонько 12 Вольт, как и предполагалось.
К этим же клеммах цепляем и наш осциллограф
Смотрим осциллограмму:
Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.
[quads id=1]
Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.
Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку 😉
Теперь начинается самое интересное. Берем наш ЛАТР
Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт.
Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.
Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:
Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.
Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма
и вот эта осциллограмма
Чем то похожи? Но чем???
Среднеквадратичное значение напряжения — это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном.
То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.
Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух
Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:
Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉
Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение.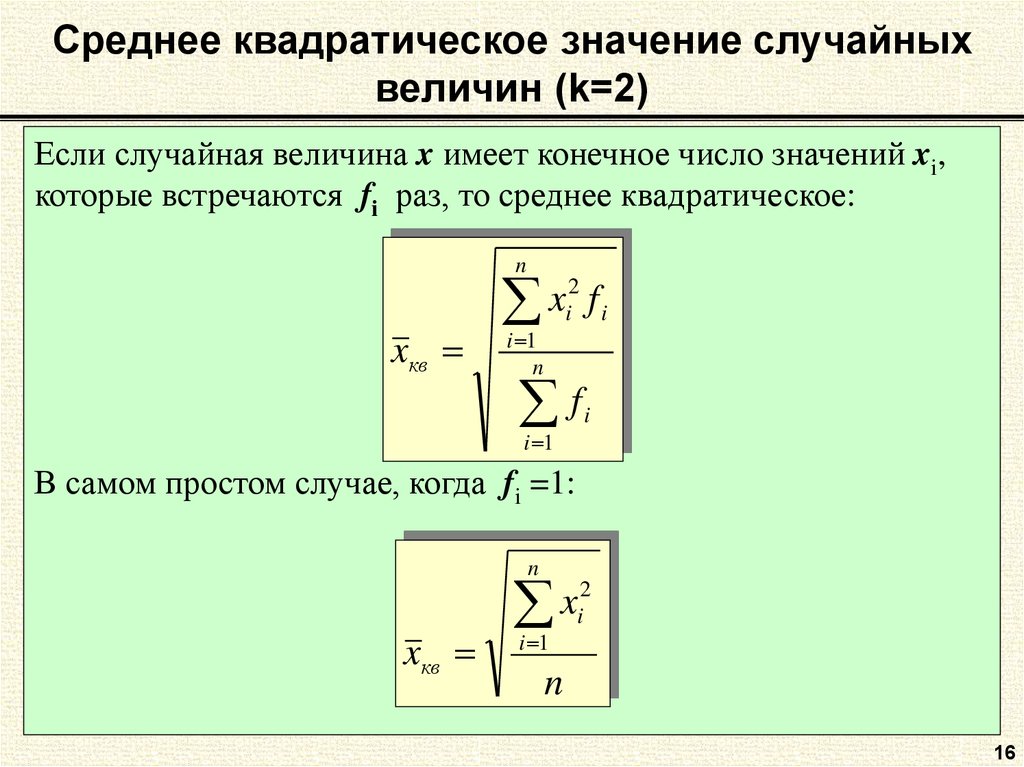
Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.
Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!
Vk — это и есть среднеквадратичное напряжение этого сигнала.
Ma — это и есть Umax.
Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт.
R.M.S. VALUE – Среднеквадратичное значение за период переменного тока, напряжения, тока, магнитного потока и т.д. Среднеквадратичное значение синусоидального тока и напряжения примерно в 2 раза меньше их амплитуды. Энциклопедический словарь
Содержание
r.m.s. (эффективное) значение переменного тока это количество постоянного тока, действие которого за один промежуток времени произведет ту же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.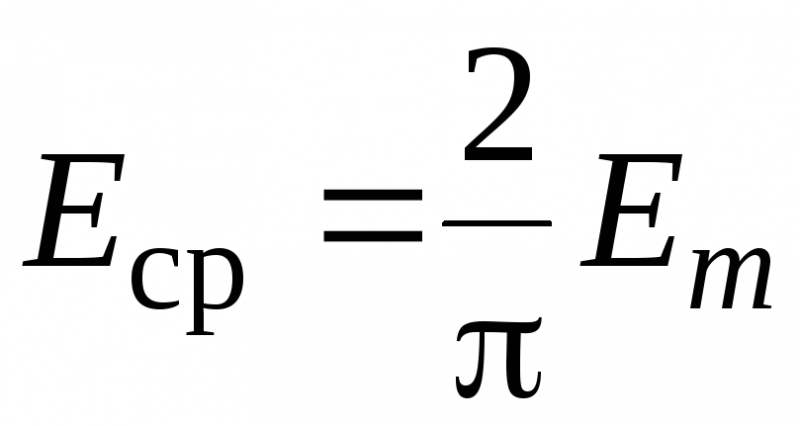
В современной литературе чаще используется математическое определение этой величины – среднеквадратичное значение переменного тока.
Другими словами, среднеквадратичное значение тока можно определить по формуле:
.
Для гармонических колебаний тока
Среднеквадратичные значения ЭДС и напряжения определяются аналогичным образом.
Количество энергии, выделяемой током с течением времени Tпериод – соответственно, равен интегралу по периоду времени Tпериод:
Уважаемые все, в прошлой статье мы затронули тему силы и работы переменного тока. Напомню, что тогда мы вычисляли его с помощью интеграла, а в самом конце статьи я сказал, что есть некоторые способы облегчить себе жизнь и часто можно обойтись без интеграла, если знать об эффективное значение текущего.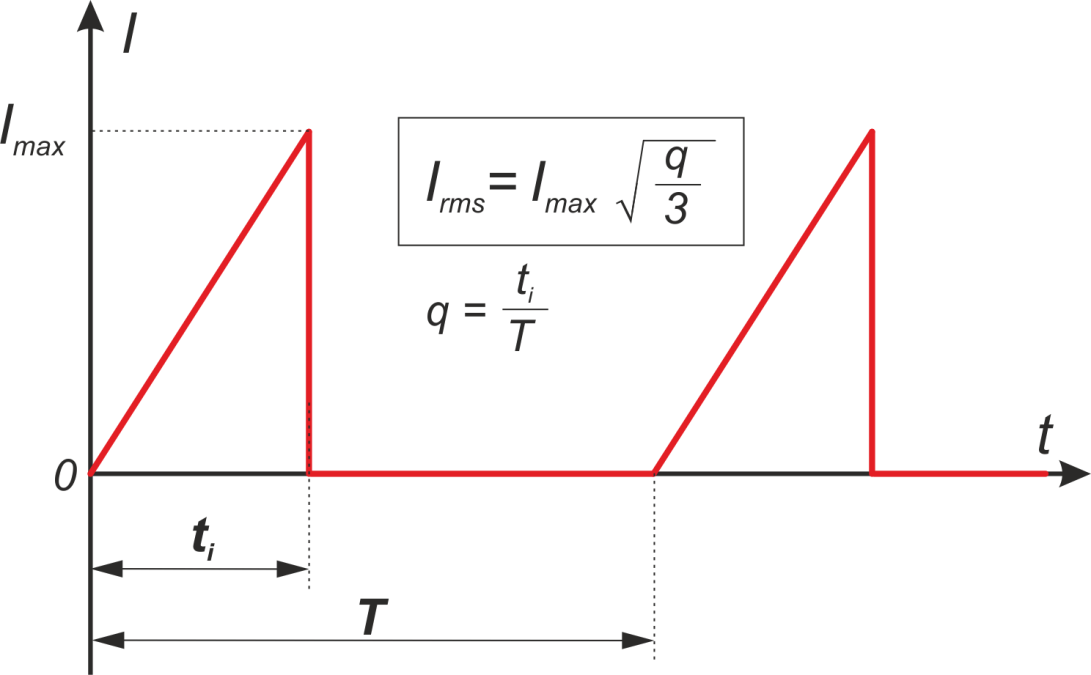
Именно об этом мы и поговорим сегодня!
Господа, наверное, ни для кого не секрет, что в природе существует множество видов переменного тока: синусоидальный, прямоугольный, треугольный и т.д. И как их вообще можно сравнивать друг с другом? По форме? Хммм… Думаю, да. Они отличаются визуально, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые люди считают, что само определение частоты применимо только к синусоидальному сигналу и не может быть применено, например, к последовательности импульсов. Формально они могут быть правы, но я не разделяю их точку зрения. Как еще его можно использовать? Например, за деньги! Неожиданно? Вовсе нет. Электроэнергия стоит денег. Вернее, электричество стоит денег. В конце концов, киловатт-часы, за которые вы все платите каждый месяц в соответствии с показаниями ваших счетчиков, – это не что иное, как работа электроэнергии. А поскольку деньги – дело серьезное, стоит ввести для них отдельный термин. Чтобы сравнить различные формы тока по количеству выполняемой ими работы, мы должны использовать термин эффективный ток.
Таким образом, Среднеквадратичное значение (или СКО) переменного тока – это значение некоторого постоянного тока, который выделит на резисторе столько же тепла, сколько выделяет наш переменный ток за время, равное периоду переменного тока. Звучит очень заумно, и, скорее всего, если вы читаете это определение впервые, вы вряд ли его поймете. Это хорошо. Когда я впервые услышал это слово в школе, мне потребовалось много времени, чтобы понять для себя, что оно означает. Поэтому сейчас я попытаюсь разобрать это определение на части, чтобы вы смогли понять, что стоит за этой запутанной фразой быстрее, чем я в свое время.
Таким образом, мы имеем дело с переменным током. Допустим, это синусоидальная волна. У него есть своя амплитуда. Аm и период Tпериод (или частота f). Фаза в данном случае не имеет значения, предположим, что она равна нулю. Этот переменный ток протекает через резистор R и энергия выделяется в этом резисторе.
За один период Tпериод нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это количество джоулей можно точно рассчитать, используя интегральные формулы, которые я приводил в прошлый раз. Предположим, мы рассчитаем, что за один период Tпериод синусоидального тока выпустит Q джоулей тепла. Обратите внимание, господа, на важный момент! Заменим переменный ток постоянным и выберем такое значение (т.е. столько ампер), чтобы на том же резисторе R в одно и то же время Tпериод одинаковое количество джоулей Q. Очевидно, что нам нужно как-то определить значение этого самого постоянного тока, эквивалентного переменному току с энергетической точки зрения. И когда мы найдем эту ценность, она будет… среднеквадратичное значение переменного тока.. Итак, господа, давайте вернемся к тому причудливому формальному определению, которое я дал в начале. Теперь это стало понятнее, не так ли?
Итак, надеюсь, суть ясна, поэтому давайте переведем вышесказанное в математику.
Как мы писали в прошлой статье, закон изменения мощности переменного тока таков
Количество энергии, выделяемой током в момент времени Tпериод – соответственно, равна интегралу от периода времени Tпериод:
Господа, теперь мы должны взять этот интеграл. Если это кажется вам слишком сложным, потому что вы не любите математику, вы можете пропустить расчеты и сразу увидеть результат. Сегодня у меня появилось настроение вспомнить молодость и тщательно проработать все эти интегралы.
Как же мы его воспринимаем? Ну, ценности, которыеm 2 и R – константы, и мы можем взять их вне знака интеграла. А для квадрата синуса мы должны использовать формулу для уменьшения степени из тригонометрии. Надеюсь, вы помните об этом. Если нет, позвольте мне напомнить вам еще раз:
Теперь разобьем интеграл на два интеграла. Мы можем использовать тот факт, что интеграл от суммы или разности равен сумме или разности интегралов.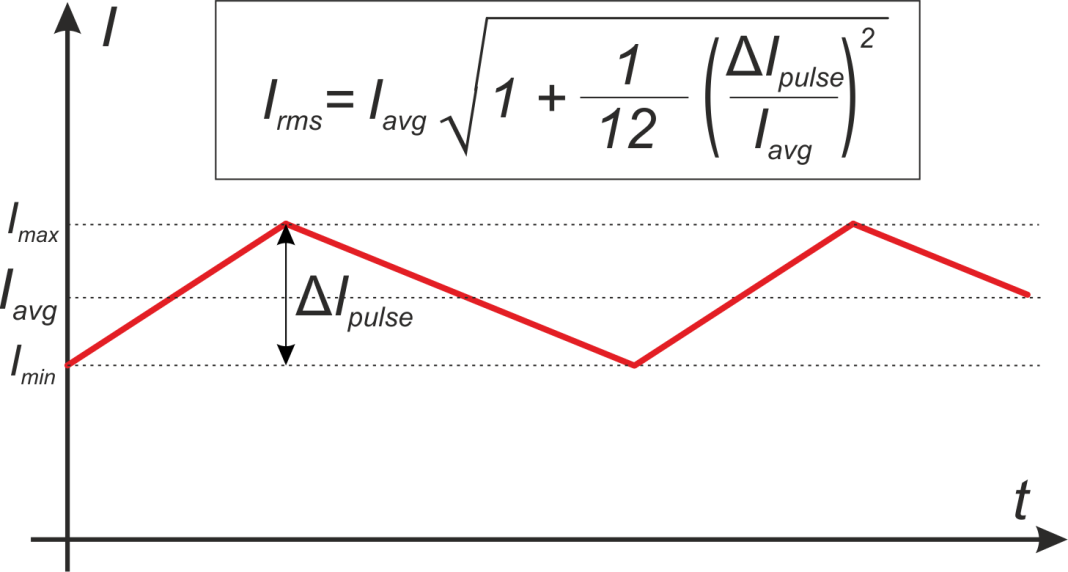
На самом деле это очень логично, если вспомнить, что интеграл – это площадь.
Господа, у меня для вас самая замечательная новость. Второй интеграл равен нулю!
Почему это так? Просто потому, что интеграл любого синуса/косинуса по кратности его периода равен нулю. Кстати, это очень полезное свойство! Я рекомендую запомнить его. Геометрически это также понятно: первая полуволна синуса проходит над осью абсцисс, и его интеграл больше нуля, а вторая полуволна проходит под осью абсцисс, поэтому его значение меньше нуля. Но они равны друг другу по модулю, поэтому их сложение (и, собственно, интеграл по всему периоду) даст в результате ноль.
Таким образом, отбросив косинусный интеграл, получаем
Не нужно быть математическим гуру, чтобы сделать вывод, что этот интеграл равен
И вот мы получаем ответ
Это дает нам количество джоулей, которые будут выделяться в резисторе R когда синусоидальный ток амплитудой Im в течение периода Tпериод.
Теперь, чтобы найти, что в данном случае среднеквадратичный ток мы должны предположить, что на том же резисторе R в одно и то же время Tпериод одинаковое количество энергии Q. Поэтому мы можем написать
Если вы не совсем понимаете, откуда берется левая часть, рекомендую повторить статью о законе Джоуля-Ленца. При этом мы выражаем среднеквадратичное значение тока I среднеквадратичное значение. от этого выражения, предварительно максимально сократив его.
Вот результат, господа. Значение r.m.s. синусоидально переменного тока в два раза меньше амплитудного значения. Хорошо запомните этот результат, это важный вывод.
В общем, никто не мешает ввести аналогию с текущими Среднеквадратичное напряжение …. В этом случае зависимость мощности от времени будет выглядеть следующим образом
Это то, что мы подставим в интеграл и выполним все преобразования.
Господа, любой из вас может сделать это на досуге, я лишь приведу конечный результат, потому что он полностью аналогичен случаю с током. Сейчас, среднеквадратичное напряжение синусоидального тока составляет
Как видите, аналогия полная. Среднеквадратичное значение напряжения также ровно в два раза больше амплитуды.
Вы можете рассчитать среднеквадратичное значение напряжения и тока практически для любой формы волны аналогичным образом: просто запишите закон мощности для сигнала и выполните физические действия, описанные выше.
Все вы, наверное, слышали, что напряжение в наших розетках составляет 220 В. Какое напряжение? Наконец, теперь у нас есть два понятия – амплитуда и среднеквадратичное значение. Оказалось, что 220 вольт в розетках – это среднеквадратичное значение! Вольтметры и амперметры в цепях переменного тока показывают среднеквадратичные значения. Форму сигнала в целом и его амплитуду в частности можно увидеть с помощью осциллографа.
Ну, мы уже говорили, что всех интересуют деньги, то есть текущая активность, а не какая-то расплывчатая амплитуда. Но давайте установим, какова амплитуда напряжения в наших сетях. Используя формулу, которую мы только что написали, мы можем написать
Это все, господа. Оказывается, в наших розетках синусоида имеет амплитуду 311 В, а не 220, как можно было бы подумать. Чтобы развеять сомнения, приведу рисунок, на котором показан закон изменения напряжения в наших розетках (напомню, что частота сети составляет 50 Гц, или, если она одинакова, период равен 20 мс). Этот закон показан на рисунке 1.
Рисунок 1 – Закон изменения напряжения в розетках
И специально для вас, джентльмены, я просмотрел напряжение на гнезде с помощью осциллографа. Я наблюдал его через делитель напряжения 1:5. Это означает, что форма сигнала будет полностью сохранена, но амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Почему я это сделал? Просто из-за большого диапазона входного напряжения все изображение не помещается на экране осциллографа.
ПРЕДУПРЕЖДЕНИЕ Если у вас нет достаточного опыта работы с высоким напряжением, если вы совершенно не представляете, как могут протекать токи во время измерений в цепях, не гальванически изолированных от сети, я определенно не рекомендую проводить такой эксперимент самостоятельно, это опасно! Дело в том, что при проведении такого рода измерений с помощью осциллографа осциллограф, подключенный к заземленной розетке существует очень высокая вероятность того, что через внутреннее заземление осциллографа произойдет короткое замыкание и прибор сгорит без возможности восстановления! И если вы сделаете эти измерения с осциллограф, подключенный к незаземленной розеткена его корпусе, кабелях и разъемах может возникнуть смертельная опасность! Это не шутка, господа, если вы не понимаете, почему это так, то лучше не делайте этого, тем более что осциллограммы уже сделаны и вы можете увидеть их на рисунке 2.
Рисунок 2 – Измерение осциллографом напряжения на розетке (делитель 1:5)
На рисунке 2 видно, что амплитуда синуса составляет около 62 В, а частота – ровно 50 Гц.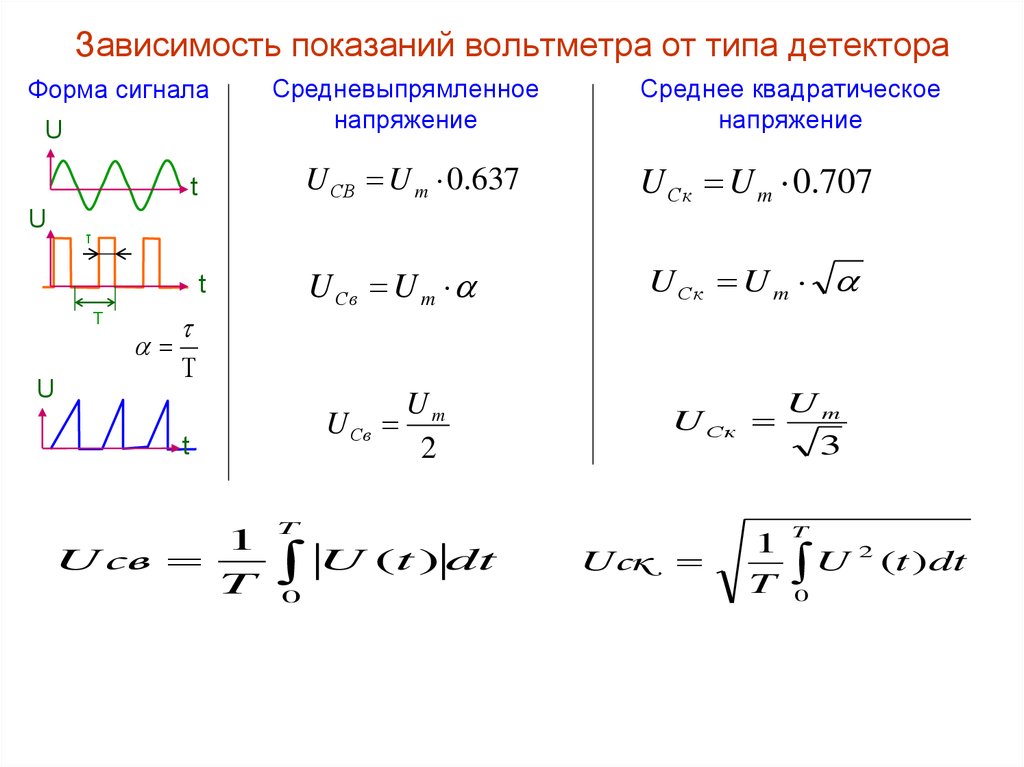
Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать фактическое значение напряжения на розетке, оно составляет
Как видите, результат измерения очень близок к теоретическому, несмотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это показывает, что все наши расчеты верны.
На сегодня это все, господа. Сегодня мы узнали, что такое r.c.m. и r.v., научились их вычислять и проверили результаты вычислений на практике. Спасибо, что прочитали это, и до встречи в будущем!
Присоединяйтесь к нашей группе в Facebook
Вопросы и предложения к администратору: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
2. Найдите постоянный ток I, который выделит такое же количество теплоты за то же время T в том же сопротивлении R. Если ток постоянен, то он равен W= = I 2 RT.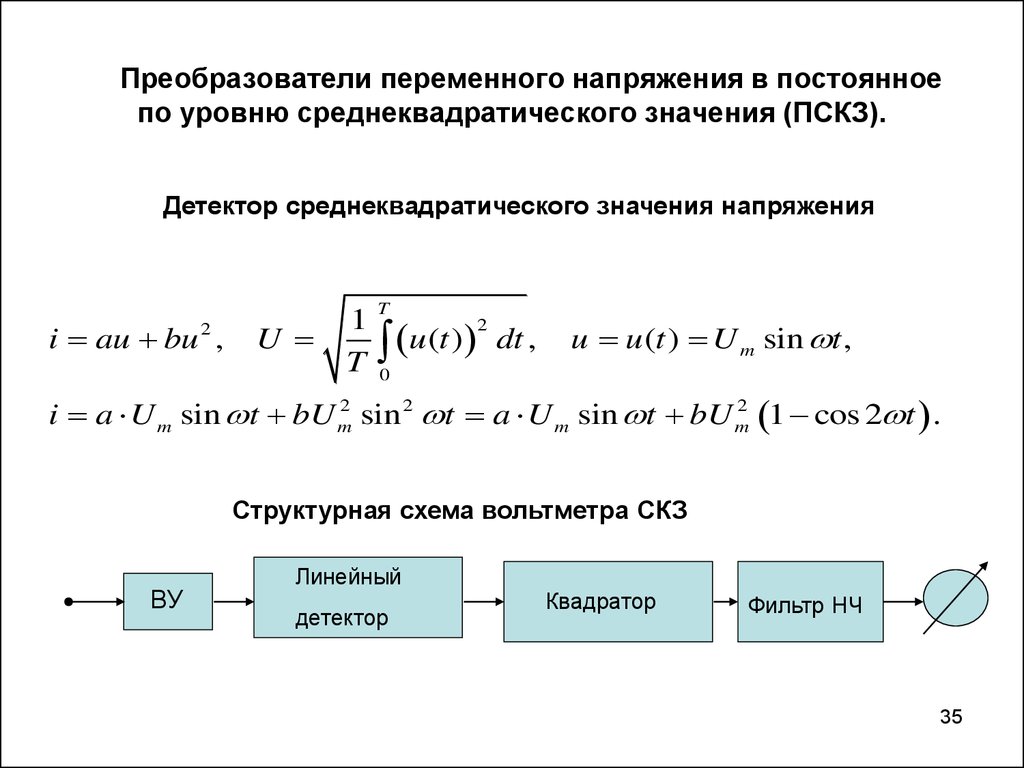
Понятие среднеквадратичного значения тока было введено из-за необходимости проведения измерений. Что можно измерить с помощью переменного тока? Если бы мы имели дело только с синусоидами – кривыми одинаковой формы – мы могли бы измерять амплитуды. На практике, однако, встречается много различных кривых, и может случиться так, что два тока разной формы имеют одинаковую амплитуду, хотя они, очевидно, будут по-разному воздействовать на электрическую цепь.
Поэтому наиболее полезно оценивать величину тока на основе работы, которую он совершает. В этой оценке сравнивается действие переменного тока с действием постоянного тока. Например, если переменный ток выделяет в цепи столько же тепла, сколько постоянный ток
10 ампер, то говорят, что этот переменный ток имеет значение 10 ампер. Это известно как среднеквадратичное значение тока.
Таким образом, значение r.m.s. переменного тока – это числовое значение такого постоянного тока, который за период времени, равный одному периоду, выделяет в резисторе такое же количество тепла, как и переменный ток.
Итак, чтобы оценить величину переменного тока, нам нужно сделать следующее.
1. Определите количество теплоты, выделяемое резистором R в момент времени T при протекании переменного тока i; это количество будет равно:
2. Выберите постоянный ток i, который отдает такое же количество теплоты за то же время T, в том же резисторе R. В случае постоянного тока это равно W= = I 2 RT.
3. Equate W≈ и W= :
Последняя формула определяет среднеквадратичное значение переменного тока.
Пример 2.1. На вход схемы подается напряжение треугольной формы импульса (рис. 2.4, а). Какова его эффективная стоимость?
Решение
Пример 2.2 . На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного полуволнового выпрямителя. Каково действующее значение напряжения, если его амплитудное значение Um был 311 V?
Решение
Пример 2.
3. Определите среднеквадратичное значение синусоидального тока.
Решение
Приведенные выше примеры показывают, что среднеквадратичное значение переменного тока зависит от его формы. Для синусоидального тока она равна амплитуде, деленной на √2.
2.4 Представление синусоидальной функции времени Предположим, что в прямоугольной системе координат существует вектор длины Imнаклоненные под углом Ψ к горизонтальной оси (рис. 2.5). Заставим этот вектор вращаться против часовой стрелки с угловой скоростью w. Затем в момент t повернется на угол wt. Проекция этого вектора на вертикальную ось имеет вид i. Из треугольника oab равен i=Im sin (ωt + Ψ)что означает, что это функция, определяющая мгновенное значение тока.
Поэтому его можно представить как проекцию на вертикальную ось вращающегося вектора. Представление тока вектором называется его векторной диаграммой. Длина вектора может быть равна амплитуде Imили до правильного значения I. Обычно вектор не показывается в произвольный момент времени tно в начальной точке (t = 0), когда угол его наклона к горизонтальной оси равен начальной фазе.
Затем, используя уравнения (2.3), строим векторную диаграмму из двух векторов – тока и напряжения (рис. 2.6).
Длины векторов равны эффективным значениям, их углы наклона к горизонтальной оси равны начальным фазам, а угол между векторами равен разности начальных фаз Ψu и Ψi, согласно уравнению (2.4), определяет сдвиг фаз напряжения и тока.
Подчеркнем, что на рисунке стрелка, указывающая на угол φвсегда направлена от вектора тока к вектору напряжения.
Теперь он направлен в положительном направлении – против часовой стрелки. Векторная диаграмма дает четкое представление о замедлении одних величин и опережении других. Если повернуть картинку, показанную на рис. 2.6, против часовой стрелки, то вектор тока будет отставать по отношению к напряжению на угол φ. Поскольку длины векторов и углы между ними не меняются при вращении, в случае, если нас не интересуют начальные фазы напряжения и тока, мы можем построить график без осей и расположить его как угодно (рис. 2.7).
Таким образом, среднеквадратичное значение тока совпадает с его среднеквадратичным значением.
Мы будем называть среднеквадратичное значение переменного тока, который создает сопротивление R во время Т в момент времени T столько же тепла, сколько переменный ток при тех же условиях. Здесь Т – период переменного тока.
Согласно закону Джоуля-Ленца, для времени dt выделяется тепло:
В течение одного периода Т выделяется тепло
– переменный ток
Уравновешивая количество выделяемого тепла, получаем где мы находим
Путем подстановки получаем
Таким образом, среднеквадратичное значение тока равно его среднеквадратичному значению.
По аналогии можно говорить о среднеквадратичных значениях ЭДС и напряжения:
Совпадение р.м.с. и р.м.с. переменного тока соответствует тому факту, что количество выделяемого тепла пропорционально квадрату силы тока.
На практике не делается различия между об.м.с. и об.п.м. переменного тока. Однако можно сказать, что р.м.с. выводится из формальных математических соображений, тогда как р.м.с. имеет вполне конкретный физический смысл.
Лист № 3.11 (312)
Переменный ток среднеквадратичного значения
Нагревательный элемент, потребляющий постоянный ток силой 5 А, доводит 1 л воды до кипения за 10 минут. Такой же эффект достигается при питании нагревателя переменным током. Определите среднеквадратичное значение переменного тока.
Подставляя значение корня из 2, получаем формулу для нахождения эффективного (среднеквадратичного) значения тока, напряжения, ЭДС – по отношению к значению амплитуды. Эта формула встречается очень часто и повсеместно используется в расчетах, касающихся цепей синусоидального переменного тока:
Что такое эффективное значение, среднеквадратичное значение, напряжение или эффективный токЧто касается величины, изменяющейся по синусоидальному (гармоническому) закону, то ее среднее значение может быть определено на половине периода.
Поскольку ток в нашей сети в подавляющем большинстве случаев синусоидальный, то для него также легко найти его среднее значение (за половину периода), просто прибегнув к операции интегрирования, установив пределы от 0 до T/2. Результат следующий:
Подставляя Pi = 3,14, находим среднее значение полупериода синусоидального тока как функцию его амплитуды. Аналогично определяется среднее значение синусоидальной ЭДС или синусоидального напряжения U:
Среднеквадратичное значение тока I или напряжения U
Однако среднее значение не так широко используется на практике, как среднеквадратичное значение синусоидального тока или напряжения. Среднеквадратичное значение изменяющейся во времени синусоидальной величины является ее действующим значением, другими словами, ее эффективной величиной.
Среднеквадратичное (или эффективное) значение тока или напряжения может быть найдено таким же образом, путем интегрирования, но с учетом квадратов и последующим извлечением квадратного корня, причем пределом интегрирования теперь является весь период синусоидальной функции.
Таким образом, для тока мы имеем:
Подставляя значение корня из 2, получаем формулу для нахождения эффективного (среднеквадратичного) значения тока, напряжения, ЭДС – относительно амплитудного значения. Эту формулу можно встретить очень часто, и она повсеместно используется в расчетах, касающихся цепей синусоидального переменного тока:
С практической точки зрения, если сравнить тепловой эффект синусоидально переменного тока с тепловым эффектом постоянного тока, за тот же период времени, при той же активной нагрузке, окажется, что тепло, выделяемое за период действия синусоидально переменного тока, равно теплу, выделяемому за тот же период времени от постоянного тока, при условии, что величина постоянного тока является корнем 2-х кратным из амплитуды переменного тока:
Это означает, что среднеквадратическое (эффективное, rms) значение синусоидального переменного тока численно равно значению постоянного тока, при котором тепловой эффект (количество выделяемого тепла) этого постоянного тока на активное сопротивление за один период синусоиды равен тепловому эффекту этого синусоидального тока за тот же период.
Аналогичным образом находится среднеквадратичное значение (эффективное, среднеквадратичное) синусоидального напряжения или синусоидальной ЭДС.
Подавляющее большинство современных портативных измерительных приборов при измерении переменного тока или напряжения отображают среднеквадратичное значение измеряемой величины, т.е. среднеквадратичное значение, а не амплитудное или среднеполупериодное.
Если на устройстве нет других спецификаций, кроме значка
U, измеряются значения тока и напряжения. Конкретные амплитудные или конкретные эффективные символы – Im (m – maximum, amplitude) или Irms (rms – Root Mean Square).
1.Определите количество теплоты, выделяемое в сопротивлении R в момент времени T при протекании переменного тока i. Это количество тепла равно:
Понятие среднеквадратичного значения тока вводится из-за необходимости проведения измерений. Что следует измерять в переменном токе? Если бы мы имели дело только с синусоидами – кривыми одинаковой формы – мы могли бы измерять амплитуды.
На практике, однако, встречаются все виды кривых, и может случиться так, что два тока разной формы имеют одинаковую амплитуду, хотя они, очевидно, будут по-разному воздействовать на электрическую цепь.
Поэтому наиболее полезно оценивать величину тока на основе работы, которую он совершает. В этой оценке сравнивается действие переменного тока с действием постоянного тока. Например, если переменный ток выделяет на участке цепи такое же количество тепла, как и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока равна 10 амперам. Это известно как среднеквадратичное значение тока.
Таким образом, значение r.m.s. переменного тока – это числовое значение такого постоянного тока, который за время, равное одному периоду, выделяет в резисторе такое же количество тепла, как и переменный ток.
Итак, чтобы оценить значение переменного тока, нам нужно сделать следующее.
1.Определите количество теплоты, выделяемое в сопротивлении R в момент времени T при протекании переменного тока i.
Это количество тепла равно:
2.Найдите постоянный ток I, который отдает такое же количество тепла в том же сопротивлении R в момент времени T. Для постоянного тока это равно: W=I2RT.
3.Мы приравниваем W=W:
Последняя формула и определяет среднеквадратичное значение переменного тока.
Пример 2.1 На вход цепи (рис. 13.1, a) подается напряжение треугольной формы. Какова его эффективная стоимость?
Рис. 13.1 – Переменные напряжения с различными формами волны
Пример 2.2 На рис. 13.1, б показана кривая напряжения на выходе однофазного полуволнового выпрямителя. Каково среднеквадратическое значение напряжения, если его амплитудное значение Um равно 311 В?
Пример 2.3 Определите среднеквадратичное значение синусоидального тока i=Imsin(ωt):
Рассмотренные примеры показывают, что среднеквадратичное значение переменного тока зависит от его формы.
Читайте далее:
Стандартные классические измерения значений напряжения (тока) основаны на двух основных методах: «среднем» и «эффективном».
«Среднее» значение функции времени — это чистая площадь функции, рассчитанная для определенного интервала времени, деленная на этот интервал времени.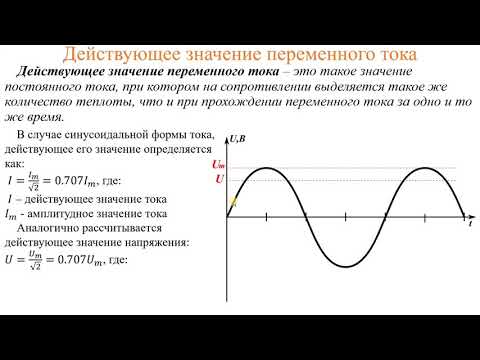
В частности,
(Уравнение 1)
Если напряжение (ток) постоянное или периодическое, то измерение его среднего значения не зависит от интервала, в течение которого производится измерение. Если, с другой стороны, функция напряжения (тока) неограниченно возрастает во времени, то среднее значение зависит от интервала измерения и не обязательно будет постоянным, т. е. среднего значения не существует. К счастью, в практическом электрическом мире значения напряжения (тока) не растут безгранично и, следовательно, имеют хорошие средние значения. Это связано с тем, что реальные источники напряжения (тока) обычно либо; (1) батареи с постоянными или медленно (экспоненциально) убывающими значениями, (2) ограниченные синусоидальные функции времени или (3) комбинации вышеперечисленного. Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение за временные интервалы, которые равны целым кратным синусоидального периода.
«Эффективное» значение симметричных периодических функций напряжения (тока) от времени основано на понятии «теплопроизводительность». Рассмотрим испытательное приспособление, показанное на рисунке 1.
Рис. 1. Тестовое приспособление
Этот сосуд изолирован и заполнен какой-либо стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия.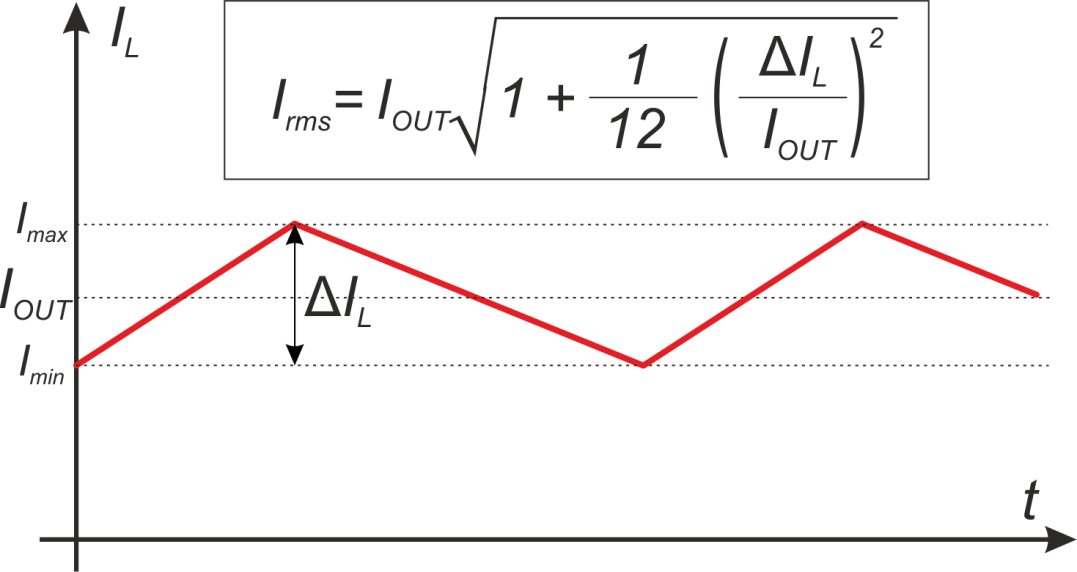
Если к внутреннему нагревателю сосуда приложить постоянное напряжение Vx, температура жидкости повысится. В конце концов, электрическая энергия, подаваемая на этот сосуд, установит равновесное состояние, при котором подведенная энергия равна потерянной энергии (теплу), а жидкость в сосуде достигнет равновесной температуры, Tx градусов.
Далее в этом экспериментальном сценарии замените источник постоянного напряжения Vx изменяющимся во времени напряжением, которое не увеличивается неограниченно. В конце концов, через некоторое время Tfinal снова установится тепловое равновесие. Если это равновесное состояние устанавливает ту же температуру Tx, которая была достигнута ранее при приложенном постоянном напряжении Vx, то можно сказать, что «эффективное» значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение «действующей стоимости». Уравнение 2 иллюстрирует это тепловое равновесие. (Уравнение 2)
Результаты этих замен показаны в уравнении 3. Уравнение 3 показывает, что эффективная эквивалентная теплоемкость ограниченной периодической функции напряжения (тока) может быть определена всего за один цикл. Это уравнение известно как старая знакомая форма «квадрата 9».0010 R является результатом M ean (среднего) S в квадрате»; отсюда и название « RMS ».
Следующие результаты могут быть показаны прямым применением уравнения 3.
Примечание: Эти примеры показывают, что форма периодической функции может определять ее среднеквадратичное значение.
Пик (гребень) функции напряжения (тока) от времени, деленный на √ 2
часто ошибочно используется для расчета среднеквадратичного значения. Этот метод может привести к ошибкам, и его явно следует избегать.
Чрезвычайно полезным фактом при определении среднеквадратичных значений является то, что любая ограниченная периодическая функция времени с хорошим поведением может быть выражена как среднее значение плюс сумма синусоид (например, теорема Фурье);
(Уравнение 4)
Где ωo — частота V(t) в радианах, а An, Bn, Ao — амплитудные коэффициенты Фурье.
Когда этот ряд подставляется в интегральное выражение (уравнение 2) для RMS, получается следующее;
(Уравнение 5)
Примечание: (A n ) 2 и (B n ) 2 /2 — квадраты среднеквадратичных значений для каждого n th Sin и Косинусная составляющая.
Ограниченная периодическая функция времени имеет среднеквадратичное значение, равное квадратному корню из суммы квадратов среднеквадратичного значения каждого отдельного компонента.
На рис. 2 показаны составные кривые, полученные путем добавления двух синусоид, одной на частоте 60 Гц и одной на частоте 180 Гц. Кривая 1 предназначена для нулевой разности фаз, а кривая 2 — для разности фаз на 90 градусов.
В частности;
Кривая 1 V(t) = 170*Sin(377*t) +50*Sin(1131*t)
Кривая 2 V(t) = 170*Sin(377*t) +50*Cos(1131*t)
Примечание: Форма комбинированной кривой определяется гармониками фазы и частоты.
Рисунок 2: Основная гармоника с добавлением третьей гармоники
Промышленные синусоидальные функции напряжения (тока) часто содержат гармоники, влияющие на форму волны и пиковые (гребенчатые) значения.
Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях с частотой 60 Гц. В недорогих устройствах для считывания среднеквадратичного значения часто используются схемы выпрямителя, фиксирующие пиковое значение, которое затем масштабируется с коэффициентом 0,707 и отображается как среднеквадратичное значение. Ясно, что этот метод может давать неверные показания среднеквадратичного значения.
В этом примере использование Vpeak ÷√2 явно дает неправильные значения.
Кривая 1: 203*0,707 = 144 В, неверное среднеквадратичное значение
Кривая 2: 155*0,707 = 110 В, неверное среднеквадратичное значение
Правильное среднеквадратичное значение для обеих составных синусоидальных функций:
[(170) 2 /2 + (50) 2 /2 ] 1/2 = 125,3 В СКЗ
Таблица 1 иллюстрирует два примера расчета среднеквадратичного значения с использованием отдельных коэффициентов Фурье и уравнения 5.
Первый пример представляет собой двухполупериодную выпрямленную синусоиду с пиковым напряжением 1 вольт. Обратите внимание, что для функции двухполупериодного выпрямления измерительному устройству, необходимому для получения показаний среднеквадратичного значения с погрешностью 0,01 %, требуется полоса пропускания, включающая пятую (5) гармонику, и разрешение для считывания уровней 10 мВ.
Другой пример, показанный в Таблице 1, представляет собой пилообразную пиковую функцию 1 В. В этом примере измерительному устройству для пилообразной функции, необходимому для получения показаний RMS с погрешностью 0,3 %, требуется полоса пропускания, включающая двадцать пятую (25) гармонику, и разрешение для считывания уровней 10 мВ.
Предположим, для наглядности, что пульсации переменного тока на выходе постоянного тока выпрямителя могут быть аппроксимированы пилообразной функцией. В таблице 1 показано, что для измерения с погрешностью 0,3 % среднеквадратичных пульсаций переменного тока на выходе постоянного тока выпрямителя с частотой 20 кГц измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для считывания уровней напряжения на 40 дБ (100 микровольт).
для пиковых пульсаций 10 мВ). Этот пример ясно показывает, что форма сигнала вместе с шириной полосы измерения и разрешением чрезвычайно важны для определения точности измерения истинного среднеквадратичного значения.
Любое устройство измерения «истинного среднеквадратичного значения» должно быть способно точно реализовать уравнение 3. Тонкость в этом утверждении заключается в том, что для электронной реализации уравнения 3 требуется, чтобы устройство имело очень большую полосу пропускания и могло разрешать малые величины.
Еще одним показателем качества, часто используемым для характеристики периодической функции напряжения (тока) во времени, является коэффициент амплитуды (CF). Крест-фактор для конкретной формы волны определяется как пиковое значение, деленное на среднеквадратичное значение. В частности,
Измерения истинного среднеквадратичного значения требуют контрольно-измерительных приборов, которые точно реализуют уравнение 3, «то самое» уравнение среднеквадратичного значения.
Эти устройства должны иметь как широкую полосу пропускания, так и хорошее низкоуровневое разрешение, чтобы поддерживать высокие коэффициенты амплитуды.
Dataforth разработала три продукта, которые удовлетворяют этим требованиям; входные модули SCM5B33, DSCA33 и 8B33 True RMS.
Эти продукты обеспечивают изолирующий барьер 1500 В среднеквадратичного значения между входом и выходом.
SCM5B33 Изолированный модуль ввода истинного среднеквадратичного значения
SCM5B33 Деталь
Технические характеристики и
Информация для заказа
(пиковое значение переменного и постоянного тока) или 10 А среднеквадратичного значения в непрерывном режимеDSCA33 Изолированный формирователь входного сигнала True RMS
DCSA33 Деталь
Технические характеристики и
Информация для заказа
90.1 Защита от переходных процессов8B33 Миниатюрный модуль ввода True RMS
8B33 Деталь
Технические характеристики и
Информация для заказа
(пиковое значение переменного и постоянного тока) или 2 действ. непрерывноВы здесь: Домашняя страница / Часто задаваемые вопросы + основы / Почему значение среднеквадратичного значения тока важно для шаговых двигателей?
Даниэль Коллинз Оставить комментарий
В большинстве прецизионных шаговых двигателей, особенно в автоматизации и управлении движением, используется метод управления, называемый микрошагом, который создает синусоидальную (или почти синусоидальную) форму волны тока, а не прямоугольная волна тока, создаваемая с типичным полноступенчатым управлением.
Номинальный ток шагового двигателя зависит от величины мощности и, следовательно, тепла, которое могут выдержать обмотки двигателя. Сила напрямую связана с сопротивлением и с числом 9.0270 квадрат тока (P = I 2 R), поэтому ток является критическим для нагрева двигателя. (Имейте в виду, что сопротивление является свойством обмоток двигателя, поэтому оно остается постоянным для данного двигателя.)
У меня 2 — доставили мотор со временем. Но поскольку синусоидальная форма волны микрошагового управления означает, что ток постоянно меняется во времени и меняет направление (с положительного на отрицательное) — во многом как форма волны переменного тока — нам нужно использовать изменяющееся во времени среднее значение тока, которое представляет собой среднеквадратичное значение или среднеквадратичное значение тока.
Среднеквадратичное значение кривой переменного тока представляет собой величину постоянного тока, которая потребуется для получения такого же количества тепла при протекании через то же сопротивление.
Среднеквадратичное значение — это статистический метод нахождения среднего значения набора значений. Чтобы найти среднеквадратичное значение, сначала возведите каждое значение в квадрат и просуммируйте квадраты. Затем разделите сумму на количество значений. Это дает вам среднее значение. Наконец, извлеките квадратный корень из среднего значения, и результатом будет среднеквадратичное значение.
Соотношение между среднеквадратичным током и пиковым током:
Это легко визуализировать, используя геометрию прямоугольного треугольника, как показано в этом посте от Lin Engineering.
Короче говоря, если вы начертите простую пошаговую последовательность (в этом примере используется 8 шагов) с током фазы A по оси X и током фазы B по оси Y, вы увидите, что максимальный или пиковый ток вдоль последовательность шагов в каждой фазе составляет 1,414 А, или 1,414-кратное среднеквадратичное значение тока 1 А. (Это упражнение работает с любым значением I СКО . Например, если I RMS равно 3 А, I пик будет 3 * 1,414 = 4,242 А.)
Изображение предоставлено Lin EngineeringГлядя на треугольник, образованный в позиции 7, и используя теорему Пифагора, вы можно вывести соотношение между пиковым и среднеквадратичным током:
Существует два основных типа шаговых приводов: приводы L/R, которые питают двигатель постоянным напряжением, и приводы с прерывателем, которые питать двигатель постоянным током. При высоких скоростях, L/R или постоянном напряжении приводы с трудом обеспечивают ток, достаточный для достижения двигателем номинального крутящего момента, из-за постоянной времени обмоток двигателя.