8-900-374-94-44
Здравствуйте, уважаемые друзья! Продолжаем изучать нашу рубрику, на очереди тема умножения и деления в Assembler. Разберемся со всеми тонкостями этих операций, конечно же, на практическом примере.
muldivИтак, как мы уже сказали, при умножении и делении в Assembler есть некоторые тонкости, о которых дальше и пойдет речь. Тонкости эти состоят в том, что от того, какой размерности регистр мы делим или умножаем многое зависит. Вот примеры:
mul bl), то значение этого регистра bl умножится на значение регистра al, а результат запишется в регистр ax, и так будет всегда, независимо от того, какой 1-байтовый регистр мы возьмем.
bl*al = axmul bx), то значение в регистре bx умножится на значение, хранящееся в регистре ax, а результат умножения запишется в регистр eax.bx*ax = eaxmul ebx), то значение в регистре ebx умножится на значение, хранящееся в регистре eax, а результат умножения запишется в 2 регистра: edx и eax.ebx*eax = edx:eaxПочти аналогично реализуется и деление, вот примеры:
div bl), то значение регистра ax поделится на значение регистра bl, результат от деления запишется в регистр al, а остаток запишется в регистр ah.
ax/bl = al, ahdiv bx), то процессор поделит число, старшие биты которого хранит регистр dx, а младшие ax на значение, хранящееся в регистре bx. Результат от деления запишется в регистр ax, а остаток запишется в регистр dx.(dx,ax)/bx = ax, dxdiv ebx), то процессор аналогично предыдущему варианту поделит число, старшие биты которого хранит регистр edx, а младшие eax на значение, хранящееся в регистре ebx. Результат от деления запишется в регистр eax, а остаток запишется в регистр edx.(edx,eax)/ebx = eax, edxДалее перейдем к примеру: он не должен вызвать у вас каких либо затруднений, если вы читали наши предыдущие статьи, особенно важна статья про вывод на экран, советую вам с ней ознакомиться.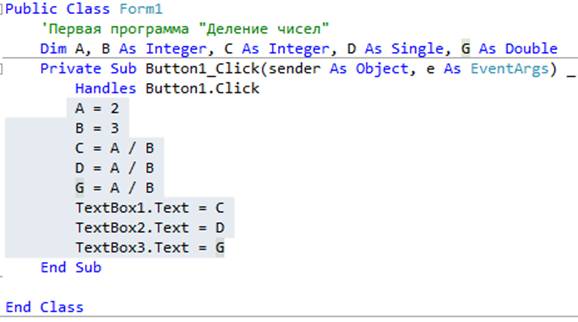
Ну а мы начнем:
.386 .model flat,stdcall option casemap:none include ..\INCLUDE\kernel32.inc include ..\INCLUDE\user32.inc includelib ..\LIB\kernel32.lib includelib ..\LIB\user32.lib BSIZE equ 15 .data ifmt db "%d", 0 ;строка формата stdout dd ? cWritten dd ? CRLF WORD ? .data? buf db BSIZE dup(?) ;буфер
Стандартное начало, в котором мы подключаем нужные нам библиотеки и объявляем переменные для вывода чисел на экран. Единственное о чем нужно сказать: новый для нас раздел .data? Знак вопроса говорит о том, что память будет выделяться на этапе компилирования и не будет выделяться в самом исполняемом файле с расширением .exe (представьте если бы буфер был большего размера) . Такое объявление — грамотное с точки зрения программирования.
.code start: invoke GetStdHandle, -11 mov stdout,eax mov CRLF, 0d0ah ;-------------------------деление mov eax, 99 mov edx, 0 mov ebx, 3 div ebx invoke wsprintf, ADDR buf, ADDR ifmt, eax invoke WriteConsoleA, stdout, ADDR buf, BSIZE, ADDR cWritten, 0 invoke WriteConsoleA, stdout, ADDR CRLF, 2, ADDR cWritten,0
В разделе кода, уже по традиции, считываем дескриптор экрана для вывода и задаем значения для перевода каретки.
Затем помещаем в регистры соответствующие значения и выполняем деление регистра ebx, как оно реализуется описано чуть выше. Думаю, тут понятно, что мы просто делим число 99 на 3, что получилось в итоге выводим на экран консоли.
;-------------------------умножение mov bx, 4 mov ax, 3 mul bx invoke wsprintf, ADDR buf, ADDR ifmt, eax invoke WriteConsoleA, stdout, ADDR buf, BSIZE, ADDR cWritten, 0 invoke ExitProcess,0 end start
Думаю, что здесь тоже все понятно и без комментариев. Как производиться умножение в Assembler вы тоже можете прочитать чуть выше, ну и результат выводим на экран.
Этот код я поместил в файл seventh.asm, сам файл поместил в папку BIN (она появляется при установке MASM32). Далее открыл консоль, как и всегда, с помощью команды cd перешел в эту папку и прописал amake.bat seventh. Скомпилировалось, затем запускаю исполняемый файл и в консоли получаются такие числа:
Как видите, мы правильно посчитали эти операции.
На этом сегодня все! Надеюсь вы научились выполнять деление и умножение на Assembler.
Скачать исходники
LOCALS .model small .stack 100h .data CrLf db 0Dh, 0Ah, '$' PromptGetX db 'Input X : ', '$' PromptGetY db 'Input Y: ', '$' KeyBuf db 7, 0, 8 dup(0) ;max,len,string,CR(0dh) msgError db 'Ошибка ввода числа', 0Dh, 0Ah, '$' X db ? Y db ? F db ? .code main proc mov ax, @data mov ds, ax @@GetX: ; ввод числа с клавиатуры (строки) lea dx, PromptGetX mov ah,09h int 21h mov ah, 0Ah mov dx, offset KeyBuf int 21h ; перевод строки (на новую строку) lea dx, CrLf mov ah,09h int 21h ; преобразование строки в число lea si, KeyBuf+1 lea di, X call Str2Num ; проверка на ошибку jnc @@GetY ; если есть ошибка ввода - напечатать сообщение об ошибке lea dx, msgError mov ah,09h int 21h jmp @@GetX @@GetY: ; ввод числа с клавиатуры (строки) lea dx, PromptGetY mov ah,09h int 21h mov ah, 0Ah mov dx, offset KeyBuf int 21h ; перевод строки (на новую строку) lea dx, CrLf mov ah,09h int 21h ; преобразование строки в число lea si, KeyBuf+1 lea di, Y call Str2Num ; проверка на ошибку jnc @@Calc ; если есть ошибка ввода - напечатать сообщение об ошибке lea dx, msgError mov ah,09h int 21h jmp @@GetY @@Calc: mov ax, 0 ;bx:=96*X mov al, X mov cl, 5 sal ax, cl mov bx, ax sal ax, 1 add bx, ax mov cl, 4 ;bx:=(96*X)/16 sar bx, cl mov bx, 9 ;ax:=Y mov al, Y sub ax, bx ;ax:=Y-(96*X)/16 call Show_AX mov ax, 4C00h int 21h main endp ; выводит число из регистра AX на экран ; входные данные: ; ax - число для отображения Show_AX proc push ax push bx push cx push dx push di mov cx, 10 xor di, di ; di - кол.цифр в числе ; если число в ax отрицательное, то ;1) напечатать '-' ;2) сделать ax положительным or ax, ax jns @@Conv push ax mov dx, '-' mov ah, 2 ; ah - функция вывода символа на экран int 21h pop ax neg ax @@Conv: xor dx, dx div cx ; dl = num mod 10 add dl, '0' ; перевод в символьный формат inc di push dx ; складываем в стэк or ax, ax jnz @@Conv ; выводим из стэка на экран @@Show: pop dx ; dl = очередной символ mov ah, 2 ; ah - функция вывода символа на экран int 21h dec di ; повторяем пока di<>0 jnz @@Show pop di pop dx pop cx pop bx pop ax ret Show_AX endp ; преобразования строки в число ; на входе: ; ds:[si] - строка с числом ; ds:[di] - адрес числа ; на выходе ; ds:[di] - число ; CY - флаг переноса (при ошибке - установлен, иначе - сброшен) Str2Num proc push ax push bx push cx push dx push ds push es push si push ds pop es mov cl, ds:[si] xor ch, ch inc si mov bx, 10 xor ax, ax ;если в строке первый символ '-' ; - перейти к следующему ; - уменьшить количество рассматриваемых символов cmp byte ptr [si], '-' jne @@Loop inc si dec cx @@Loop: mul bx ; умножаем ax на 10 ( dx:ax=ax*bx ) mov [di], ax ; игнорируем старшее слово cmp dx, 0 ; проверяем, результат на переполнение jnz @@Error mov al, [si] ; Преобразуем следующий символ в число cmp al, '0' jb @@Error cmp al, '9' ja @@Error sub al, '0' xor ah, ah add ax, [di] jc @@Error ; Если сумма больше 65535 cmp ax, 8000h ja @@Error inc si loop @@Loop pop si ;проверка на знак push si inc si cmp byte ptr [si], '-' jne @@Check ;если должно быть положительным neg ax ;если должно быть отрицательным jmp @@StoreRes @@Check: ;дополнительная проверка, когда при вводе положительного числа получили отрицательное or ax, ax ; js @@Error @@StoreRes: ;сохранить результат mov [di], ax clc pop si pop es pop ds pop dx pop cx pop bx pop ax ret @@Error: xor ax, ax mov [di], ax stc pop si pop es pop ds pop dx pop cx pop bx pop ax ret Str2Num endp end main
Арифметические команды языка Ассемблер: аддитивные и мультипликативные команды целочисленных операций.7.1. Сложение и вычитание.
7.1.1. ADD – команда для сложения двух чисел. Она работает как с числами со знаком, так и без знака.
ADD Приемник, Источник
Логика работы команды:
<Приемник> = <Приемник> + <Источник>
Возможные сочетания операндов для этой команды аналогичны команде MOV.
По сути дела, это – команда сложения с присвоением, аналогичная принятой в языке C/C++:
Приемник += Источник;
Операнды должны иметь одинаковый размер. Результат помещается на место первого операнда.
После выполнения команды изменяются флаги, по которым можно определить характеристики результата:
Примеры:
add ax,5 ;AX = AX + 5
add dx,cx ;DX = DX + CX
add dx,cl ;Ошибка: разный размер операндов.
7.1.2. SUB — команда для вычитания одного числа из другого. Она работает как с числами со знаком, так и без знака.
SUB Приемник, Источник
Логика работы команды:
<Приемник> = <Приемник> — <Источник>
Возможные
сочетания операндов для этой команды аналогичны команде MOV.
По сути дела, это – команда вычитания с присвоением, аналогичная принятой в языке C/C++:
Приемник -= Источник;
Операнды должны иметь одинаковый размер. Результат помещается на место первого операнда.
На самом деле вычитание в процессоре реализовано с помощью сложения. Процессор меняет знак второго операнда на противоположный, а затем складывает два числа.
Примеры:
sub ax,13 ;AX = AX — 13
sub ax,bx ;AX = AX + BX
sub bx,cl ;Ошибка: разный размер операндов.
7.1.3. Инкремент и декремент. Очень часто в программах используется операция прибавления или вычитания единицы. Прибавление единицы называется инкрементом, а вычитание — декрементом. Для этих операций существуют специальные команды процессора: INC и DEC. Эти команды не изменяют значение флага
Эти команды содержит один операнд и имеет следующий синтаксис:
INC Операнд
DEC Операнд
Логика работы команд:
INC: <Операнд> = < Операнд > + 1
DEC: <Операнд> = < Операнд > — 1
В качестве
инкремента допустимы регистры и память: reg, mem.
Примеры:
inc ax ;AX = AX + 1
dec ax ;AX = AX — 1
7.1.4. NEG – команда для изменения знака операнда.
Синтаксис:
NEG Операнд
Логика работы команды:
<Операнд> = – < Операнд >
В качестве декремента допустимы регистры и память: reg, mem.
Примеры:
neg ax ;AX = -AX
7.2. Сложение и вычитание с переносом.
В системе команд процессоров x86 имеются специальные команды сложения и вычитания с учётом флага переноса (CF). Для сложения с учётом переноса предназначена команда ADC, а для вычитания — SBB. В общем, эти команды работают почти так же, как ADD и SUB, единственное отличие в том, что к младшему разряду первого операнда прибавляется или вычитается дополнительно значение флага CF.
Они позволяют
выполнять сложение и вычитание многобайтных целых чисел, длина которых больше,
чем разрядность регистров процессора (в нашем случае 16 бит).
Принцип
программирования таких операций очень прост — длинные числа складываются
(вычитаются) по частям. Младшие разряды складываются(вычитаются) с помощью
обычных команд ADD и SUB, а затем последовательно складываются(вычитаются)
более старшие части с помощью команд ADC и SBB. Так как эти команды учитывают
перенос из старшего разряда, то мы можем быть уверены, что ни один бит не
потеряется. Этот способ похож на сложение(вычитание) десятичных чисел в
столбик.
На следующем рисунке показано сложение двух двоичных чисел командой ADD:
При сложении происходит перенос из 7-го разряда в 8-й, как раз на границе между байтами. Если мы будем складывать эти числа по частям командой ADD, то перенесённый бит потеряется и в результате мы получим ошибку. К счастью, перенос из старшего разряда всегда сохраняется в флаге CF. Чтобы прибавить этот перенесённый бит, достаточно применить команду ADC:
Пример:
#include <iostream.h>
#include <iomanip.h>
void main()
{
//Сложение двух чисел с учетом переноса: FFFFFFAA + FFFF
int a, b;
asm {
mov eax, 0FFFFFFAAh
mov ebx, 0FFFFh
mov edx, 0
mov ecx, 0
add eax, ebx
adc edx, ecx
mov a, edx
mov b, eax
}
cout << hex << a << setw(8) << setfill(‘0’) << b; //10000ffa9
}
7.
3. Умножение и деление.
7.3.1. MUL – команда умножения чисел без знака. У этой команды только один операнд — второй множитель, который должен находиться в регистре или в памяти. Местоположение первого множителя и результата задаётся неявно и зависит от размера операнда:
Размер операнда | Множитель | Результат |
1 байт | AL | AX |
2 байта | AX | DX:AX |
4 байта | EAX | EDX:EAX |
Отличие умножения
от сложения и вычитания в том, что разрядность результата получается в 2 раза
больше, чем разрядность сомножителей.
Примеры:
mul bl ;AX = AL * BL
mul ax ;DX:AX = AX * AX
Если старшая часть результата равна нулю, то флаги CF и ОF будут иметь нулевое значение. В этом случае старшую часть результата можно отбросить.
7.3.2. IMUL – команда умножения чисел со знаком. Эта команда имеет три формы, различающиеся количеством операндов:
1. С одним операндом — форма, аналогичная команде MUL. В качестве операнда указывается множитель. Местоположение другого множителя и результата определяется по таблице.
2. С двумя операндами — указываются два множителя. Результат записывается на место первого множителя. Старшая часть результата в этом случае игнорируется. Кстати, эта форма команды не работает с операндами размером 1 байт.
3. С тремя операндами — указывается
положение результата, первого и второго множителя. Второй множитель должен быть
непосредственным значением. Результат имеет такой же размер, как первый
множитель, старшая часть результата игнорируется.
Это форма тоже не работает с
однобайтными множителями.
Примеры:
imul cl ;AX = AL * CL
imul bx,ax ;BX = BX * AX
imul cx,-5 ;CX = CX * (-5)
imul dx,bx,134h ;DX = BX * 134h
CF = OF = 0, если произведение помещается в младшей половине результата, иначе CF = OF = 1. Для второй и третьей формы команды CF = OF = 1 означает, что произошло переполнение.
7.3.3. DIV – команда деления чисел без знака. У этой команды один операнд — делитель, который должен находиться в регистре или в памяти. Местоположение делимого, частного и остатка задаётся неявно и зависит от размера операнда:
Размер
операнда | Делимое | Частное | Остаток |
1 байт | AX | AL | AH |
2 байта | DX:AX | AX | DX |
4 байта | EDX:EAX | EAX | EDX |
При выполнении команды DIV может возникнуть прерывание (в данном курсе прерывания мы рассматривать не будем поэтому старайтесь избегать таких случаев):
Примеры:
div cl ;AL = AX / CL, остаток в AH
div di ;AX = DX:AX / DI, остаток в DX
7.3.4. IDIV – команда деления чисел со знаком. Единственным операндом является делитель. Местоположение делимого и частного определяется также, как для команды DIV. Эта команда тоже генерирует прерывание при делении на ноль или слишком большом частном.
7.3.5. NOP – ничего не делающая команда.
Синтаксис:
NOP
Примеры:
nop
Пример. (5 + 8) / (2 * 3)
#include <iostream.h>
void main()
{
asm {
mov bx, 5 //BL = 5
add bx, 8 //BL = BL + 8 | 13
sub bx, 1 //BL = BL — 1 | 12
mov al, 2 //AL = 2
mov cl, 3 //CL = 3
mul cl //AX = AL * CL | 6
//AX = 6, BL = 12
xchg bx, ax //AX = 12, BX = 6
mov dx, 0
div bx
}
}
Цель
работы: изучение операций сложения,
вычитания, умножения и деления двоичных
чисел на языке Ассемблер.
Регистры общего назначения AX, BX, CX и DX
Регистры общего назначения являются основными рабочими регистрами ассемблерных программ. Их отличает то, что к ним можно адресоваться одним словом или однобайтовым кодом. Левый байт считается старшим, а правый — младшим.
Регистр AX – является основным сумматором и применяется во всех операциях ввода/вывода, в некоторых операциях со строками и в некоторых арифметических операциях. Например, команды умножения, деления и сдвига предполагают использование регистра АХ.
АХ: \ АН \ АL\
Регистр BX — базовый регистр, единственный из регистров общего назначения, используемый в индексной адресации. Кроме того, регистр BX используется при вычислениях.
BX: \ BH \ BL \
Регистр
CX
— является счётчиком. Он необходим
для управления числом повторений циклов
и для операций сдвига влево или вправо
и для вычислений.
CX: \ CH \ CL \
Регистр DX — регистр данных. Используется в некоторых операциях ввода/вывода, в операциях умножения и деления больших чисел совместно с регистром AX.
DX: \ DH \ DL \
Любой из регистров общего назначения может быть использован для суммирования или вычитания 8- , 16- или 32- разрядных величин.
Команда MOV. Пересылка (байта или слова). Признаки не меняются. Рассмотрим примеры использования данной команды с применением имён, имён в квадратных скобках и чисел. В примерах предположено, что WORDAS определяет слово в памяти.
MOV AX , BX ; переслать содержимое ВX в регистр AX.
MOV AX , 28 ; переслать значение 28 в регистр AX.
MOV AX , WORDAS ; переслать WORDAS в регистр AX.
MOV AX , [ BX ] ; переслать содержимое памяти по адресу в регистре
MOV AX , [ 28 ] ; переслать содержимое по смещению 28.
Команда ADD (сложение) и SUB (вычитание) выполняют сложение и вычитание байтов или слов, содержащих двоичные данные. Вычитание осуществляется в компьютере по методу сложения с двоичным дополнением : для второго операнда устанавливаются обратные значения битов и прибавляется 1, а затем происходит сложение с первым операндом. Во всём, кроме первого шага операции сложения и вычитания идентичны. Оба операнда могут быть байтами или словами, и оба операнда могут быть двоичными числами со знаком или без знака.
Возможные ситуации сложения / вычитания: регистр – регистр; память – регистр; регистр – память; регистр – непосредственное значение; память – непосредственное значение. Например,
ADD BH , 10H ; непосредственное значение и регистр
ADD AX , BX ; регистр и регистр
ADD WORDAS , CX ; память и регистр
ADD AX , [DX] ; регистр и память
SUB WORDAS , BX ; регистр из памяти
SUB BX , 100H ; непосредственное значение из регистра
SUB WORDAS , 16H ; непосредственное значение из памяти
Один
байт содержит знаковый бит и семь битов
данных, т.
е. результат арифметической
операции может легко превзойти ёмкость
регистра, и возникает переполнение.
Полное слово имеет также ограничение,
что ограничивает возможности компьютера
для выполнения арифметических операций.
Поэтому используют специальные
сопроцессоры, которые быстро и эффективно
выполняют эти операции, представляя
числа в специальных кодах. Иногда вместо
команды ADD
используется команда ADC — сложения
с переносом, которая складывает два
значения и если флаг уже установлен, к
сумме прибавляется 1. Для аналогичных
целей (вычитание с заёмом) вместо команды
SUB
используется команда SBB.
Числовое содержимое поля может интерпретироваться по разному. Многие числовые поля являются беззнаковыми, например номер абонента, адрес памяти. Некоторые числовые поля предполагаются всегда положительными, например норма выплаты, день недели, число PI. Другие числовые поля являются знаковыми, так как их содержимое может быть положительным и отрицательным. Команды ADD и SUB не делают разницы между знаковыми и беззнаковыми данными, они просто складывают и вычитают биты.
Например, для беззнакового числа биты представляют число 249, а для знакового –7:
Как и все остальное в assembly, существует множество способов умножения и деления.
lea (только умножение).Разрушение мифов
потому что они требуют много циклов CPU
MUL и IMUL невероятно быстры на современных CPU, см.: http:/ / www.agner.org / optimize/instruction_tables. pdf DIV и IDIV всегда были чрезвычайно медленными.
Пример для Intel Skylake (стр. 217):
MUL, IMUL r64: задержка 3 цикла, обратная пропускная способность 1 цикл.
Обратите внимание, что это максимальная задержка для умножения двух 64 ! битовые значения.
CPU может выполнять одно из этих умножений каждый цикл CPU, если все, что он делает, — это умножение.
Если учесть, что приведенный выше пример с использованием сдвигов и сложений для умножения на 7 имеет задержку в 4 цикла (3 с использованием lea). Нет никакого реального способа победить простое умножение на современном CPU.
Умножение на обратное
Согласно инструкции ASM lib Agner Fog Страница 12 :
Деление происходит медленно на большинстве микропроцессоров. В вычислениях с плавающей запятой мы можем сделать несколько делений с одним и тем же делителем быстрее, умножив их, например, на обратное:
float a, b, d; a /= d; b /= d;может быть изменен на:
float a, b, d, r; r = 1.0f / d; a *= r; b *= r;Если мы хотим сделать что-то подобное с целыми числами, то мы должны масштабировать обратный делитель на 2n, а затем сдвинуть n мест вправо после умножения.
Умножение на обратное хорошо работает, когда вам нужно разделить на константу или если вы делите на одну и ту же переменную много раз подряд.
Вы можете найти действительно классный код assembly, демонстрирующий эту концепцию, в библиотеке assembly Агнера Фога .
Сдвиги и добавления / замены
Сдвиг вправо — это деление на два shr — (R ед.).
Сдвиг влево-это умножение на два shl — (L arger).
Вы можете добавлять и вычитать, чтобы исправить Не-степени двух по пути.
//Multiply by 7
mov ecx,eax
shl eax,3 //*8
sub eax,ecx //*7
Деление, отличное от степеней 2, с использованием этого метода быстро усложняется.
Вы можете задаться вопросом, почему я выполняю операции в странном порядке, но я пытаюсь сделать цепочку зависимостей как можно короче, чтобы максимизировать количество инструкций, которые могут выполняться параллельно.
Использование Lea
Lea-это инструкция для вычисления смещений адресов.
Он может вычислять кратные 2,3,4,5,8 и 9 в одной инструкции.
Вот так:
//Latency on AMD CPUs (K10 and later, including Jaguar and Zen)
//On Intel all take 1 cycle.
lea eax,[eax+eax] //*2 1 cycle
lea eax,[eax*2+eax] //*3 2 cycles
lea eax,[eax*4] //*4 2 cycles more efficient: shl eax,2 (1 cycle)
lea eax,[eax*4+eax] //*5 2 cycles
lea eax,[eax*8] //*8 2 cycles more efficient: shl eax,3 (1 cycle)
lea eax,[eax*8+eax] //*9 2 cycles
Обратите внимание, однако, что lea с множителем (масштабным коэффициентом) считается инструкцией ‘complex’ на AMD CPUs от K10 до Zen и имеет задержку 2 CPU циклов. На более ранних AMD CPUs (k8) lea всегда имеет 2-тактную задержку даже при простом режиме адресации [reg+reg] или [reg+disp8] .
ДРАМ
Таблицы инструкций Agner Fog неверны для AMD Zen: 3-компонентный или масштабируемый индекс LEA по-прежнему составляет 2 цикла на Zen (только 2 на тактовую пропускную способность вместо 4) в соответствии с InstLatx64 (http://instlatx64.atw.hu/ ). кроме того, как и ранее CPUs, в режиме 64-bit lea r32, [r64 + whatever] имеет задержку в 2 цикла. Таким образом, на самом деле быстрее использовать lea rdx, [rax+rax] вместо lea edx, [rax+rax] на AMD CPUs, в отличие от Intel, где усечение результата до 32 бит является бесплатным.
*4 и *8 можно сделать быстрее, используя shl , потому что простой сдвиг занимает всего один цикл.
С другой стороны, lea не изменяет флаги и позволяет свободно перемещаться в другой регистр назначения.
Поскольку lea может сдвигаться влево только на 0, 1, 2 или 3 бита (то есть умножаться на 1, 2, 4 или 8), это единственные разрывы, которые вы получаете.
Intel
На Intel CPUs (семейство Sandybridge) любой 2-компонентный LEA (только один + ) имеет задержку в один цикл. Таким образом, lea edx, [rax + rax*4] имеет задержку в один цикл, но lea edx, [rax + rax + 12] имеет задержку в 3 цикла (и худшую пропускную способность). Пример этого компромисса подробно обсуждается в коде C++ для проверки гипотезы Коллатца быстрее, чем написанный от руки assembly-почему? .
Данная группа команд реализует четыре основные арифметические операции – сложение, вычитание, умножение и деление. С точки зрения типов операндов, арифметические команды можно разделить на работающие с целыми и вещественными операндами.
Арифметические команды имеют следующий формат Fppp (для вещественных операндов) или FIppp (для целочисленных операндов), где ррр может принимать значения:
Возможны следующие комбинации операндов:
Fppp (FIppp) — выполняет операцию над ST(0) — приемник и ST(1) — источник. Результат заносится в регистр стека сопроцессора ST(0).
Fppp (FIppp) — выполняет операцию над значением ST(0) и источником. Результат заносится в регистр стека сопроцессора ST(0).
Fppp (FIppp) , — выполняет операцию над значением в регистре стека сопроцессора ST(i) и значением в вершине стека ST(0). Результат заносится в регистр ST(i).
FpppP (FIpppР) , — операция выполняется аналогично предыдущей команде, только последним действием команды является выталкивание значения из вершины стека сопроцессора ST(0). Результат сложения остается в регистре ST(i-1).
В чем заключается «обратность» вычитания и деления?
Проанализируйте описание этих двух команд и Вам все станет понятно:
FSUB st(i), st — команда вычитает значение в вершине стека SТ(0) из значения в регистре стека сопроцессора ST(i). Результат вычитания запоминается в регистре стека сопроцессора ST(i).
FSUBR st(i),st — команда вычитает значение в вершине стека ST(0) из значения в регистре стека сопроцессора ST(i). Результат вычитания запоминается в вершине стека сопроцессора — регистре ST(0).
Пример: сложение трех чисел: .data Sarray dd 1.5, 3.4, 6.6 ;объявим массив вещественных чисел, котрые мы хотим сложить Sum dd ? ;зарезервируем место для результата .code Finit ;инициализируем сопроцессор Fld Sarray ;загрузим первый элемент Sarray Fadd Sarray+4 ;прибавим к вершине второй элемнт массива Fadd Sarray+8 ;и третий туда же Fstp Sum ;выгрузим значение из вершины стека сопроцессора в переменную Sum
Дополнительные арифметические команды
В данном приложении приводятся файлы, используемые при выполнении заданий к лабораторной работе № 1. Файл hello.exe может быть запущен на исполнение для отработки простого диалога с программой, так и загружен в отладчик TD, для изучения возможностей последнего при отладке ассемблерных программ. Файлы из группы – Mov.asm, Arithmet.asm Logical.asm, LoopCall.asm – демонстрируют применение соответствующей группы команд с использованием различных видов адресации. Поэтому после трансляции их загружают только в TD с целью просмотра форматов машинных команд процессора при изучении принципов их кодирования.
%TITLE «Демонстрационный файл Hello.asm«
IDEAL
MODEL small
STACK 256
DATASEG
Promt DB ‘Это время после полудня? (Да/Нет – y/n)$’
GoodMorning DB 13,10,’Доброе утро!’,13,10,’$’
GoodAfternoon DB 13,10,’Здравствуйте!’,13,10,’$’
CODESEG
Start: mov ax,@data ;Установка в ds адреса сегмента
mov ds,ax ;данных
mov dx,OFFSET Promt ;Сообщение-запрос
mov ah,9 ;Функция DOS вывода сообщения
int 21h ;на экран
mov ah,1 ;Функция DOS ввода символа с
int 21h ;клавиатуры
cmp al,’y’ ;y?
jz IsAfternoon ;да, время после полудня
cmp al,’n’ ;n?
jz IsMorning ;нет, до полудня
IsAfternoon: mov dx,OFFSET GoodAfternoon ;Указание на «Здравствуйте»
jmp SHORT Disp
IsMorning: mov dx,OFFSET GoodMorning ;Указание на «Доброе утро»
Disp: mov ah,9 ;Функция DOS вывода сообщения на
int 21h ;экран
Exit: mov ax,4C00h ;Функция DOS- выход из программы
int 21h ;Вызов DOS. Останов программы.
END Start ;Конец программы/точка входа
%TITLE «Команды MOV и режимы адресации. Файл Mov.asm«
IDEAL
MODEL small
STACK 256
value = 528
DATASEG
b_x DB 1,2,4
w_x DW 8,16,32,64
Label b_var byte
w_var DW 1234h ;Число в памяти: 34h(мл. байт):12h(ст. байт)
CODESEG
Start: mov ax,@data ;Установка в ds адреса
mov ds,ax ;сегмента данных.
;Непосредственная адресация.
mov al,255 ;255=0FFh-беззнаковое число
mov ah,-1 ;[4] ;-1=0FFh-отрицательное число
mov ax,value/5+20 ;[5] ;Загрузка в ах константного выражения
mov bx,offset w_x; ;[6] ;Адрес переменной w_x в bx (bx=0003h)
;Регистровая и прямая адресации. Символьная переменная, заключённая в квадратные
;скобки (например [b_x]), – выполняет роль адреса этой переменной в памяти
mov dl,al ;[7]
mov al,[b_x] ;В al занести содержимое переменной b_x, т. е. al=b_x[0]=01h.
mov dx,[w_x] ;dx=w_x[0]=0008h.
mov si,[w_var] ;si=1234h
mov al,[b_var] ;al=[b_var]=34h
mov ah,[b_var+1] ;ah=[b_var+1]=12h
;Косвенная регистровая.
mov cx,[bx] ;[13] ;cx=w_x[0]=0008h, т.к. bx=offset w_x
mov [word bx],-2 ;[14] ;w_x[0]= -2=0FFFEh.
;Базовая адресация.
mov ax,[bx+2] ;[15] ;ax=w_x[1]=16=0010h.
mov [word bx+2],24 ;[16] ;w_x[1]=24=0018h.
;Индексная адресация.
mov si,1
mov al,[si+b_x] ;[18] ;al=[b_x+1]=02h.
;Базово индексная адресация.
inc si ;si=2
mov bx,1 ;bx=2
mov ax,[bx+si+w_x] ;[21] ;ax=[4+w_x]=32=0020h.
mov [word bx+si+w_x],128 ;[22] ;w_x[2]=128=0080h.
;Применение команды lea
lea bx,[w_x+si] ;[23] ;bx=offset w_x+si=offset w_x[1]=005h.
Exit: mov ax,4C00h ;Функция DOS- выход из программы.
int 21h ;Вызов DOS. Останов
END Start ;Конец программы/точка входа.
%TITLE «Команды сложения, умножения и деления. Файл Arithmet.asm«
IDEAL
MODEL small
STACK 256
DATASEG
op_1 DD 11112222h
op_2 DD 3333DDDEh
b_dst DB 32 ;20h
b_src DB 64 ;40h
w_src DW 512 ;200h
CODESEG
Start: mov ax,@data ;Установка в ds адреса
mov ds,ax ;сегмента данных.
;Сложение операндов из двойных слов.
mov di,offset op_1
mov si,offset op_2
mov ax,[di] ;Low(op_1)®ax.
add ax,[si] ;[6] ;Low(op_1)+Low(op_2)=Low(sum).
mov [di],ax ;Сохранение Low(sum).
mov ax,[di+2] ;High(op_1)®ax.
adc ax,[si+2] ;[9] ;High(op_1)+High(op_2)+cf=High(sum).
mov [di+2],ax ;Сохранение High(sum).
;Умножение и деление.
mov al,[b_dst] ;al=32=20h.
Push al
mul [b_src] ;[13] ;ax ¬al*[b_src]- беззнаковое умножение: «8*8=16»
neg [b_src] ;[14] ;[b_src]¬0-[b_src]
pop al
imul [b_src] ;[16] ;ax ¬al*[b_src]- знаковое умножение: «8*8=16»
idiv [b_src] ;[17] ;{al= Quot (ax/[b_src]), ah=Rem (ax/[b_src])} – знако-
;вое деление: «16:8=8»
cbw ;al®ax (со знаком). В данном случае ax>0
mul [w_src] ;[19 ] ;dx:ax¬ax*[w_src]- беззнаковое умножение: «16*16=32»
idiv [w_src] ;[20 ] ;{ax¬Quot (dx.ax/w_src), dx¬Rem (dx.ax/w_src)} –
;знаковое деление в формате: «32:16=16». Так как операнды положительные, то такой же
;результат можно было бы получить и с помощью команды div
Exit: mov ax,4C00h ;Функция DOS -выход из программы.
int 21h ;Вызов DOS. Останов.
END Start ;Конец программы/точка входа.
%TITLE «Логические команды и команды сдвига. Файл Logical.asm«
IDEAL
MODEL small
STACK 256
DATASEG
source DW 0ABh
w_mask DW 0F0h
oper DB 0AAh ;176
CODESEG
Start: mov ax,@data ;Установка в ds адреса сегмента
mov ds,ax ;данных.
mov ax,[source] ;Занести в ax,bx,cx, [source]=0ABh
mov bx,ax
mov cx,ax
;Стандартное применение логических команд
and ax,[w_mask] ;[6] ;Стирание соответствующих битов
or bx,[w_mask] ;[7] ;Установка соответствующих битов в «1»
xor cx,[w_mask] ;Инвертирование соответствующих битов
xor bx,bx ;bx=0. Гашение регистра
;Циклические сдвиги.
rol [oper],1 ;[10] ;[oper]=55, cf=1.
ror [oper],1 ;[oper]=AA, cf=1.
rcl [oper],1 ;[12] ;[oper]=55, cf=1.
rcr [oper],1 ;[oper]=AA, cf=1.
;Нестандартное применение – быстрое деление положительного числа сдвигами вправо.
mov al,0Eh ;al=0Eh=14
sar al,1 ;[15] ;al=07 ,cf=0,
sar al,1 ;al=03 ,cf=1,
sar al,1 ;al=01 ,cf=1,
sar al,1 ;al=00 ,cf=1.
;Быстрое умножение сдвигами влево положительного числа: A=10*x=(4+1)*2*x; x=al.
mov al,2 ;al=2
mov bl,al
sal al,1 ;[21] ;*2,
shl al,1 ;*4,
add al,bl ;*(4+1),
shl al,1 ;*10, al=10*x=20=14h.
Exit: mov ax,4C00h ;Функция DOS -выход из программы.
int 21h ;Вызов DOS. Останов.
END Start ;Конец программы/точка входа.
%TITLE «Цикл с подпрограммой. Файл LoopCall.asm«
;В программе демонстрируется организация цикла на основе команды Loop в процессе деле-
;ния каждого элемента массива Array на постоянное число с использованием соответствую-
;щей процедуры Divide
IDEAL
MODEL small
STACK 256
DATASEG
Array DB 20,25,30,35,40
LengArray = $-Array ;длина строки
CODESEG
Start: mov ax,@data ;Установка в ds адреса сегмента
mov ds,ax ;данных.
mov si,offset Array
mov cx,LengArray
L1: mov al,[si] ;al¬текущий элемент строки.
call Divide ;[6] ;Выполнение процедуры деления на 5.
mov [si],al
inc si
loop L1 ;[9] ;Повторить сх раз
Exit: mov ax,4C00h ;Функция DOS -выход из программы.
int 21h ;Вызов DOS. Останов.
;Подпрограмма деления Divide на 5. Вход: al-значение, предназначенное для деления.
;Выход: al-результат деления.
PROC Divide near ;Оператор near можно не указывать, т.к. модель
;памяти Small предполагает все переходы близкими
push bx
xor ah,ah ;Подготовка ah:al как 16-битовое
mov bl,5 ;делимое, а bl- 8-битовый делитель.
div bl ;al<quot(ax/bl), ah<-rem(ax/bl)
pop bx
ret ;[18] ;Возврат из процедуры
ENDP Divide
END Start ;Конец программы/точка входа.
Использование процессораКак и все остальное в ассемблере, есть много способов умножения и деления.
lea (только умножение).Разрушение мифов
, потому что они требуют большого количества циклов ЦП
MUL и IMUL невероятно быстры на современных процессорах, см. Http: // www.agner.org/optimize/instruction_tables.pdf
DIV и IDIV работают и всегда были чрезвычайно медленными.
Пример для Intel Skylake (стр. 217):
MUL, IMUL r64: Задержка 3 цикла, обратная пропускная способность 1 цикл.
Обратите внимание, что это максимальная задержка при умножении на два 64! битовые значения.
ЦП может выполнять одно из этих умножений в каждом цикле ЦП, если все, что он делает, — это умножения.
Если учесть, что в приведенном выше примере с использованием сдвигов и сложения для умножения на 7 задержка составляет 4 цикла (3 с использованием lea).На современном процессоре нет реального способа превзойти простое умножение.
Умножение на обратную
Согласно инструкции Agner Fog asm lib на странице 12:
Деление работает медленно на большинстве микропроцессоров. С плавающей запятой вычисления, мы можем сделать несколько делений с одним и тем же делителем быстрее, умножив на обратную, например:
поплавок a, b, d; а / = d; b / = d;можно изменить на:
поплавок a, b, d, r; г = 1.0f / d; а * = г; б * = г;Если мы хотим сделать что-то подобное с целыми числами, мы должны масштабировать обратный делитель на 2n, а затем сдвинуть n разрядов на сразу после умножения.
Умножение на обратное хорошо работает, когда вам нужно разделить на константу или если вы делите на одну и ту же переменную много раз подряд.
Вы можете найти действительно крутой ассемблерный код, демонстрирующий концепцию, в ассемблерной библиотеке Агнера Фога.
Сдвиг и добавление / подпрограмма
Сдвиг вправо — это деление на два shr — ( R educe).
Сдвиг влево — это умножение на два shl — ( L arger).
Вы можете складывать и вычитать, чтобы корректировать не степени двойки по пути.
// Умножить на 7
mov ecx, eax
shl eax, 3 // * 8
sub eax, ecx // * 7
Деление, отличное от степени двойки, при использовании этого метода быстро усложняется.
Вы можете задаться вопросом, почему я выполняю операции в странном порядке, но я пытаюсь сделать цепочку зависимостей как можно короче, чтобы максимально увеличить количество инструкций, которые могут выполняться параллельно.
Использование Lea
Lea — это инструкция для вычисления смещения адресов.
Он может вычислять кратные 2,3,4,5,8 и 9 за одну инструкцию.
Как так:
// Задержка на процессорах AMD (K10 и новее, включая Jaguar и Zen)
// На Intel все занимают 1 цикл.
lea eax, [eax + eax] // * 2 1 цикл
lea eax, [eax * 2 + eax] // * 3 2 цикла
lea eax, [eax * 4] // * на 4 цикла эффективнее: shl eax, 2 (1 цикл)
lea eax, [eax * 4 + eax] // * 5 2 цикла
lea eax, [eax * 8] // * 8 на 2 цикла эффективнее: shl eax, 3 (1 цикл)
lea eax, [eax * 8 + eax] // * 9 2 цикла
Обратите внимание, что lea с множителем (масштабным коэффициентом) считается «сложной» инструкцией на процессорах AMD от K10 до Zen и имеет задержку в 2 цикла процессора.На более ранних процессорах AMD (k8) lea всегда имеет двухцикловую задержку даже в простом режиме адресации [reg + reg] или [reg + disp8] .
AMD
Таблицы инструкций Агнера Фога неверны для AMD Zen: 3-компонентный или масштабируемый индекс LEA по-прежнему составляет 2 цикла в Zen (с пропускной способностью только 2 на такт вместо 4) в соответствии с InstLatx64 (http: // instlatx64. atw.hu/). Также, как и более ранние процессоры, в 64-битном режиме lea r32, [r64 + любой] имеет задержку в 2 цикла.Так что на самом деле быстрее использовать lea rdx, [rax + rax] вместо lea edx, [rax + rax] на процессорах AMD, в отличие от Intel, где усечение результата до 32 бит является бесплатным.
* 4 и * 8 можно сделать быстрее, используя shl , потому что простой сдвиг занимает всего один цикл.
С положительной стороны, lea не изменяет флаги и позволяет свободный переход к другому регистру назначения.
Поскольку lea может сдвигаться влево только на 0, 1, 2 или 3 бита (то есть умножение на 1, 2, 4 или 8), это единственные разрывы, которые вы получаете.
Intel
На процессорах Intel (семейство Sandybridge) любой двухкомпонентный LEA (только один + ) имеет задержку в один цикл. Итак, lea edx, [rax + rax * 4] имеет задержку в один цикл, но lea edx, [rax + rax + 12] имеет задержку в 3 цикла (и худшую пропускную способность). Пример этого компромисса подробно обсуждается в коде C ++ для проверки гипотезы Коллатца быстрее, чем рукописная сборка — почему ?.
Поскольку Z80 не имеет встроенных инструкций умножения, когда программист хочет произвести умножение, он должен выполнить это вручную.Программист может взять процедуру умножения из книги или журнала, которая не обязательно может быть оптимизирована для конкретного случая (или вообще оптимизирована), или он может даже использовать процедуру, которая работает, добавляя одно и то же значение n раз, то есть в значительной степени худшее решение проблемы.
В этой статье представлены оптимизированные методы умножения. Сначала он знакомит вас с умножением с использованием сдвигов, которые очень быстрые и могут использоваться, если один из параметров умножения является фиксированным числом.Далее, он предоставляет ряд оптимизированных общих подпрограмм умножения и деления для различной битовой глубины и даже подпрограмму извлечения квадратного корня.
Когда вы сдвигаете регистр на 1 бит влево, вы умножаете значение регистра на 2. Этот сдвиг можно выполнить с помощью инструкции SLA r. Последовательно выполняя несколько сдвигов, вы можете очень легко умножить на любую степень 2. Например:
л.д. б, 3; Умножить 3 на 4
sla b; x4
sla b; результат: b = 12
Если вы используете регистр A, вы можете быстрее умножать с помощью инструкции ADD A, A, которая составляет 5 T-состояний на инструкцию вместо 8.Таким образом, ADD A, A в точности совпадает с SLA A или умножением на два. Кстати, вместо использования ADD A, A вы также можете использовать RLCA, который фактически ведет себя так же.
л.д. а, 15; Умножить 15 на 8
добавить a, a; x8
добавить, а
добавить a, a; результат: a = 120
При программировании умножения вы всегда должны быть уверены, что результат никогда не превысит 255, другими словами, перенос может не произойти. В этом случае RLCA фактически действует иначе, чем SLA A или ADD A, A (в некоторых случаях более полезно, в некоторых случаях менее полезно).Но, как правило, это не вызывает беспокойства, потому что, когда регистр A переполняется, результат обычно не имеет особого смысла.
Если вы хотите умножить на другое значение, кроме степени двойки, вы почти всегда можете достичь желаемого результата, сохраняя промежуточные значения во время сдвига и добавляя или вычитая их впоследствии. Несколько примеров:
л.д. а, 5; Умножьте 5 на 20 (= A x 16 + A x 4)
добавить a, a; x16
добавить, а
ld b, a; Сохраните значение A x 4 в B
добавить, а
добавить, а
добавить a, b; Добавьте A x 4 к A x 16, результат: a = 100
Если вы хотите умножить на 22, вы также должны сохранить значение после первого прибавления в регистре и затем прибавить его к общей сумме.
Иногда вы также можете использовать вычитания для более быстрого достижения целей. Например, умножение A на 15. Это можно сделать, используя метод, описанный выше, однако в этом случае вам понадобятся 4 временных регистра и четыре дополнительных добавления впоследствии. Это можно было бы лучше сделать следующим образом, для чего требуется еще 1 умножение, но затем используется только 1 временный регистр и 1 вычитание:
л.д. а, 3; Умножьте 3 на 15 (= A x 16 - A x 1)
ld b, a; Сохранить значение A x 1 в B
добавить a, a; x16
добавить, а
добавить, а
добавить, а
sub b; результат: a = 45
Так вот, деление очень похоже на умножение.Если процедура умножения сложна, процедура деления еще более сложна. Однако, используя сдвиги, слишком легко разделить в Assembly. Это делается простым смещением в другую сторону, вправо. Для этого следует использовать инструкцию SRL r. Пример:
л.д. б, 3; Разделить 18 на 4
srl b; x4
srl b; результат: b = 4 (остальные 2 потеряны)
Нет реальной быстрой альтернативы сдвигу вправо при использовании регистра A. В качестве альтернативы вы можете использовать для этого RRCA.Однако при использовании RRCA необходимо убедиться, что отдыха не будет, иначе результат не будет правильным. Это может быть достигнуто операцией AND к исходному значению со значением, очищающим младшие биты (которые в противном случае были бы вывернуты), или путем использования значений, которые всегда кратны разделителю.
л.д. а, 153; Разделить 153 на 8
и a,% 11111000; Очистить биты 0–2 (равно 256–8)
rrca; / 8
rrca
rrca; результат: a = 19
Деление со значениями, отличными от степени двойки, сложнее и часто невозможно.Если вы хотите убедиться в этом сами, попробуйте построить процедуру, которая делит 100 на 20. Чтобы узнать, можно ли разделить значение, вы должны посмотреть на количество завершающих нулей в двоичном представлении этого значения. В этом случае максимальное количество RRCA, которое вы можете использовать, равно этому количеству. Если вы посмотрите на вышеупомянутое значение 100 в двоичном формате (% 01100100), вы увидите, что там два конечных нуля. Поэтому в подпрограмме деления можно использовать только 2 RRCA, тогда как для деления на 20 требуется 4 из них.
Откровенно говоря, если у вас нет очень жесткого контроля над значениями, которые задаются в качестве параметра, вряд ли возможно деление на значения, которые не являются степенью двойки.При использовании такого метода, как умножение, деление, например, на 3, конечно, возможно, но только если все входные значения четны и все кратны 3. Если любое из этих условий не выполняется, результат будет некорректным.
Есть также способы сдвига 16-битных регистров. Это делается с помощью 8-битного сдвига в сочетании с 8-битным поворотом и битом переноса. Чтобы сдвинуть регистр DE на один бит влево, вы должны использовать:
слэ
rl d
Чтобы сдвинуть его на один бит вправо (теперь с BC в качестве примера), используйте:
srl b
rr c
К сожалению, обычно эти 16-битные сдвиги довольно медленны по сравнению с 8-битными сдвигами (которые чаще всего происходят в быстром регистре A, что делает их почти в 4 раза быстрее).Однако, как и в случае с 8-битными сдвигами, есть также возможность выполнять более быстрые 16-битные сдвиги влево с помощью инструкции ADD.
доп. Гл., Гл .; сдвинуть HL на 1 бит влево ... hl = hl x 2
Итак, лучший способ умножить 16-битные значения — использовать регистр HL в сочетании с инструкциями ADD HL, HL.
Ну вот и все, что можно сказать о сдвигах и умножениях / делениях. Есть еще несколько второстепенных приемов, но на самом деле все, что я могу сказать об этом, — это просто проявить немного творчества.
Наконец, я расскажу вам, насколько мне известно, самые быстрые из возможных универсальных процедур умножения и деления. Эти процедуры следует использовать, когда:
Вы также можете использовать их, если хотите, чтобы ваш код выглядел действительно аккуратно, и не особо заботитесь о скорости.Что касается их внутреннего устройства, все, что я скажу о нем, — это то, что они работают так же, как вы научились решать умножения и деления в начальной школе. Но на самом деле это не имеет значения. Просто скопируйте их в свою программу как (развернутые) подпрограммы или, если вы хотите удалить любое понятие структурированного программирования, как встроенный код или макрос.
Да, и если у вас действительно очень низкие переменные коэффициенты умножения, вы можете использовать ужасный метод умножения на добавление x-раз-цикла.Наверное, быстрее.
Это подпрограммы умножения с вращением влево. Их скорость в основном довольно постоянна, хотя в зависимости от количества единиц в первичном множителе может быть небольшая разница в скорости (1 обычно занимает на 7 состояний больше времени, чем 0).
;
; Умножение 8-битных значений
; В: Умножить H на E
; Out: HL = результат
;
Mult8:
ld d, 0
ld l, d
ЖК б, 8
Mult8_Loop:
добавить hl, hl
младший NC, Mult8_NoAdd
добавить hl, de
Mult8_NoAdd:
djnz Mult8_Loop
Ret
;
; Умножьте 8-битное значение на 16-битное значение
; В: Умножить A на DE
; Out: HL = результат
;
Mult12:
ld l, 0
ЖК б, 8
Mult12_Loop:
добавить hl, hl
добавить, а
младший NC, Mult12_NoAdd
добавить hl, de
Mult12_NoAdd:
djnz Mult12_Loop
Ret
;
; Умножение 16-битных значений (с 16-битным результатом)
; В: Умножение BC на DE
; Out: HL = результат
;
Mult16:
ld a, b
ЖК б, 16
Mult16_Loop:
добавить hl, hl
sla c
rla
младший NC, Mult16_NoAdd
добавить hl, de
Mult16_NoAdd:
djnz Mult16_Loop
Ret
;
; Умножение 16-битных значений (с 32-битным результатом)
; В: Умножение BC на DE
; Выход: BCHL = результат
;
Mult32:
ld a, c
ld c, b
ld hl, 0
ЖК б, 16
Mult32_Loop:
добавить hl, hl
rla
rl c
младший NC, Mult32_NoAdd
добавить hl, de
adc a, 0
jp nc, Mult32_NoAdd
inc c
Mult32_NoAdd:
djnz Mult32_Loop
ld b, c
ld c, a
Ret
Умножения с правым вращением в основном не сильно отличаются от умножений с левым вращением.Они используют очень похожий процесс, и количество шагов в расчете одинаковое. Однако на Z80 умножения с левым вращением можно кодировать намного быстрее и компактнее, поэтому во всех предыдущих подпрограммах использовались варианты с левым вращением.
Однако у делений, вращающихся вправо, есть одно довольно приятное преимущество, которое состоит в том, что он должен выполнять цикл только до тех пор, пока не закончатся биты, после чего он может быть завершен без каких-либо дополнительных операций. Таким образом, если значение на самом деле использует только 4 бита (например, число 11), процедура должна выполняться только 4 цикла и может быть завершена впоследствии с помощью быстрой условной проверки, поэтому для этого потенциально большого ускорения практически не требуется дополнительных усилий.
Глядя на приведенную ниже таблицу с расчетами скорости подпрограммы Mult12R и учитывая тот факт, что оптимальный левовращающийся Mult12 (развернутый) принимает 268 T-состояний (включая состояния M1, что в основном означает 1 дополнительное состояние для каждой инструкции), вы можете увидеть, что в граница эффективности составляет 4 бита. Более того, обычный Mult12 работает быстрее. Однако 4-битный Mult12, конечно, снова будет более быстрым, поэтому, чтобы воспользоваться этим, большинство, но не все значения должны попадать в 4-битный диапазон.
Сколько времени занимает n-битное умножение (в среднем):
1-битное: 78,5 T-состояний
2-битное: 140 T-состояний
3-битное: 201,5 T-состояний
4-битное: 263 T- состояний
5-бит: 324,5 T-состояний
6-бит: 386 T-состояний
7-бит: 447,5 T-состояний
8-бит: 509 T-состояний
Важно отметить, что это может показаться быстрым, но не забывайте, что количество битов и возможные значения связаны друг с другом в логарифмической шкале. Поэтому, если вы используете случайные байтовые значения, количество значений в 4-битном диапазоне составляет только 1 из каждых 16 значений.Чтобы лучше понять, что это означает, взгляните на следующую таблицу, в которой указана средняя скорость, которую вы можете ожидать для случайного значения в определенном домене.
Средние скорости в указанном домене:
| <0,255> | 447,980 T-состояния |
| <0,127> | 386,961 T-состояния |
| <0,6322> 90,4268 -состояние | |
| <0,31> | 266.844 T-состояния |
| <0,15> | 209,188 T-состояния |
| <0,7> | 155,375 T-состояния |
| <0,3> | 109,25 T-состояния |
| <0,1> | 78,5 T-состояния |
Итак, в заключение, если вы делаете большое количество умножений, одно из значений в основном меньше 6 бит, например, если ваши данные логарифмические , использование алгоритма вращения вправо было бы самым быстрым выбором.В качестве примера реального использования эта процедура может быть применима, например, к вычислениям частотных таблиц в проигрывателе музыки, которые задаются в логарифмической шкале.
Ну вот собственно рутина. Обратите внимание, что ее можно легко преобразовать в подпрограмму Mult8R, вставив инструкцию ld d, 0 сразу после ld hl, 0, а также что развертывание этой подпрограммы не даст вам дополнительной скорости..
;
; Умножьте 8-битное значение на 16-битное значение (вращение вправо)
; В: Умножить A на DE
; Поместите наименьшее значение в A для наиболее эффективного расчета
; Out: HL = результат
;
Mult12R:
ld hl, 0
Mult12R_Loop:
srl a
jr nc, Mult12R_NoAdd
добавить hl, de
Mult12R_NoAdd:
Sla E
rl d
или
jp nz, Mult12R_Loop
Ret
Для полноты картины здесь также пример развернутой процедуры умножения с вращением влево.Это занимает немного больше места, но работает значительно быстрее. На самом деле он все еще довольно компактный, всего 41 байт. В среднем на это требуется 268 T-состояний (включая ожидания M1). Минимум — 235 состояний, максимум — 301 тик.
Между прочим, я рассмотрел возможность использования той же техники, что и при умножении с правым вращением в этой процедуре, это довольно легко сделать, поместив переходы между ними в список add hl, hl. Однако потеря скорости, вызванная дополнительными прыжками, не перевешивает выигрыш, и в любом случае это вряд ли практично, поскольку это применимо к nr.битов, используемых слева (число 128 будет использовать 1 бит, а 64 — два).
;
; Умножение 8-битного значения на 16-битное значение (развернутое)
; В: Умножить A на DE
; Out: HL = результат
;
Mult12U:
ld l, 0
добавить, а
младший NC, Mult12U_NoAdd0
добавить hl, de
Mult12U_NoAdd0:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd1
добавить hl, de
Mult12U_NoAdd1:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd2
добавить hl, de
Mult12U_NoAdd2:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd3
добавить hl, de
Mult12U_NoAdd3:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd4
добавить hl, de
Mult12U_NoAdd4:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd5
добавить hl, de
Mult12U_NoAdd5:
добавить hl, hl
добавить, а
младший NC, Mult12U_NoAdd6
добавить hl, de
Mult12U_NoAdd6:
добавить hl, hl
добавить, а
ret nc
добавить hl, de
Ret
Также стоит развернуть другие процедуры умножения.Например, для процедуры Mult8 она сохраняет 115 из 367 T-состояний в среднем, что на 31% быстрее, всего за 38 байт (14 → 52).
Прежде чем мы перейдем к реальным процедурам деления, при делении необязательно использовать (более медленные) процедуры деления. Не забывайте, умножение и деление связаны. Если вы хотите разделить на 2, вы также можете умножить на 0,5. Преобразуя это в эти подпрограммы, чтобы разделить 8-битное значение на другое 8-битное значение (как это делает Div8), вы можете вызвать подпрограмму Mult8 с параметром 1 (1 / первое 8-битное значение * 256) и параметром 2 другое 8-битное значение.Результирующее слово будет шестнадцатеричным значением с фиксированной точкой с запятой между старшим и младшим байтами.
Например, вычислите 55/11:
Вход A: # 18 (1/11 * 256 = 23,272727, округлено до 24)
Вход B: # 37 (55)
Выход: # 528 (# 5,28 или 5,15625 в десятичной системе)
Обратите внимание, что результат не совсем верное значение (которое должно было быть # 500), потому что 1/11 на самом деле не очень хорошее число, как в десятичном представлении (.0
), так и в шестнадцатеричном представлении (#.1745D1). Если бы мы округлили значение не до # .18, а до # .17, что было бы правильным округлением, результат был бы # 4F1. Это было бы более точным, чем текущий результат, однако наша цель — написать оптимальный код, и выделить правильно округленное целое число из этого результата (равного 5) было бы намного проще, если бы в результате у нас получилось # 528, потому что мы тогда можно просто взять только старший байт. Также для «правильного округления» потребуется дополнительный код. Вот почему мы округлили значение.Если взять слишком большое базовое значение, ошибка накапливается. Если вы, например, попытаетесь разделить 2200 на 11, результатом будет 206, тогда как должно было быть 200. Для решения этой проблемы вы можете либо увеличить разрешение (используйте 16-битное значение деления (# .1746) и 24 — или 32-битный результат) или разделите на значения, которые являются «аккуратными» в шестнадцатеричной системе счисления (являющиеся степенями двойки). Однако также помните, что независимо от того, какую базу вы используете, будь то 10 или 16, у вас всегда будут подразделения, которые приводят к ошибкам.Значения, с которыми это происходит, различаются, но вам придется иметь дело с ограничениями разрешения и округлением.
В любом случае. Это общие распорядки деления. Медленнее, чем процедуры умножения, но все же максимально быстро и, вероятно, очень полезно.
;
; Разделить 8-битные значения
; В: Разделить E на делитель C
; Выходы: A = результат, B = отдых
;
Div8:
xor a
ЖК б, 8
Div8_Loop:
rl e
rla
sub c
младший NC, Div8_NoAdd
добавить a, c
Div8_NoAdd:
djnz Div8_Loop
ld b, a
ld a, e
rla
cpl
Ret
;
; Разделить 16-битные значения (с 16-битным результатом)
; В: Разделить BC на делитель DE
; Аут: BC = результат, HL = отдых
;
Div16:
ld hl, 0
ld a, b
ЖК б, 8
Div16_Loop1:
rla
adc hl, hl
sbc hl, de
младший NC, Div16_NoAdd1
добавить hl, de
Div16_NoAdd1:
djnz Div16_Loop1
rla
cpl
ld b, a
ld a, c
ld c, b
ЖК б, 8
Div16_Loop2:
rla
adc hl, hl
sbc hl, de
младший NC, Div16_NoAdd2
добавить hl, de
Div16_NoAdd2:
djnz Div16_Loop2
rla
cpl
ld b, c
ld c, a
Ret
Спасибо Flyguille за подпрограмму Div16, взятую из его исходного кода MNBIOS.
Подпрограммы деления также можно развернуть, чтобы получить хороший прирост скорости. Если вы возьмете, например, подпрограмму Div16, для завершения требуется 1297 T-состояний. Однако в развернутом состоянии ему нужно всего 1070 T-состояний, что означает увеличение скорости на 18%. Дополнительная стоимость в байтах составляет 146 байтов (исходная процедура — 27 байтов).
Рикардо Биттенкур предоставил нам быструю процедуру деления на 9. Она создана для .dsk или подпрограммы ROM. Это очень быстро, но работает только в диапазоне 0–1440.
;
; деление на девять
; введите HL = число от 0 до 1440
; выход A = HL / 9
; уничтожить HL, DE
; Z80 R800
DIV9: INC HL; 7 1
LD D, H; 5 1
LD E, L; 5 1
ДОБАВИТЬ HL, HL; 12 1
ДОБАВИТЬ HL, HL; 12 1
ДОБАВИТЬ HL, HL; 12 1
SBC HL, DE; 17 2
LD E, 0; 8 2
LD D, L; 5 1
LD A, H; 5 1
ДОБАВИТЬ HL, HL; 12 1
ДОБАВИТЬ HL, HL; 12 1
ADD HL, DE; 12 1
АЦП A, E; 5 1
XOR H; 5 1
И 03FH; 8 2
XOR H; 5 1
RLCA; 5 1
RLCA; 5 1
RET; всего = 157 22
Это более быстрая процедура извлечения квадратного корня, чем та, которая была здесь ранее, результаты тестов говорят, что она на 26% быстрее.Его написал Рикардо Биттенкур, огромное ему спасибо :).
;
; Квадратный корень из 16-битного значения
; В: HL = значение
; Out: D = результат (округлено в меньшую сторону)
;
Sqr16:
ld de, # 0040
ld a, l
ld l, h
ld h, d
или
ЖК б, 8
Sqr16_Loop:
sbc hl, de
младший NC, Sqr16_Skip
добавить hl, de
Sqr16_Skip:
ccf
rl d
добавить, а
adc hl, hl
добавить, а
adc hl, hl
djnz Sqr16_Loop
Ret
Ну вот и все. Спасибо господину. Родней Закс :), за написание его книги «Программирование Z80», которая научила меня выполнять умножение на Z80 и послужила источником вдохновения для перечисленных здесь процедур.Если у вас есть предложения по повышению скорости или вы знаете другой метод, который может быть быстрее при определенных условиях, сообщите мне.
~ Grauw
Сокращенный набор команд для всех микросхем в семействе ARM — от ARM2 до StrongARM — включает странные и замечательные инструкции, такие как MLA (Умножение на Накопление: умножение на два регистров и добавить к результату содержимое трети) и ASL (арифметический сдвиг влево: полностью идентична инструкции Logical Shift Left).Более поздние чипы содержат несколько Дополнительные указания. Однако, насколько мне известно, места в набор инструкций для чего-то, что было бы очень полезно — инструкции DIV.
12 - 4 = 8 8 - 4 = 4 4-4 = 0
Когда я был совсем маленьким, мне разрешили играть со старомодными механическими счетчиками. машина. На передней панели машины было множество вертикальных циферблатов, подобных тем, что на кодовый замок, на котором вы устанавливаете числа, которые хотите вычислить, и был ручка на одной стороне, которая была намотана от вас, чтобы прибавить текущий номер к итоговое значение на дисплее или по направлению к вам, чтобы вычесть его.Чтобы осуществить разделение, нужно было установить первое число, а затем вычесть из него второе число несколько раз (считая, сколько раз вы поворачивали ручку!), как и в приведенной выше сумме. Очевидно, однако, что это могло бы быть очень медленным, если бы вы делали сумму вроде 128 ÷ 4. поскольку ответ — 32, это количество раз, которое вам придется повернуть ручку!
Было бы вполне возможно выполнить деление в коде ARM, используя эту простую технику, построив такой цикл:
MOV R1, # 128; разделить R1
MOV R2, # 4; от R2
MOV R0, # 0; инициализировать счетчик
.вычесть
SUBS R1, R1, R2; вычесть R2 из
; R1 и магазин
; результат обратно в
; R1 установка флагов
ADD R0, R0, # 1; добавить 1 к счетчику,
; НЕ устанавливаем флаги
BHI вычесть; перейти к началу
; цикл по условию
; Выше, т.е. R1 равно
; все еще больше, чем
; R2. Ответьте сейчас в R0
Поскольку даже самый медленный процессор ARM намного быстрее, чем ребенок, поворачивающий ручку, прикрепленную к жесткий набор шестерен, это может быть даже приемлемым решением.Но есть уловка обычно используется для сохранения работы на вычислительной машине — и вы также можете использовать ее на компьютере.
Используя наш пример 128 ÷ 4, вы в конечном итоге сделаете следующее:
Мы больше не можем вычесть 4 (наше исходное число), поэтому мы нашли последнюю цифру числа ответ будет 2. Другими словами, ответ будет 32, результат, который мы получили раньше, но у нас было обернуть ручку только пять раз, чтобы получить ее, а не тридцать два раза!
Вы могли заметить, что это почти тот же метод, который используется при делении с использованием ручка и бумага… «четыре в один не пойдут … четыре в двенадцать входят три раза … четыре в восемь идет дважды … ответ тридцать два «. Разница в том, что мы знаем по опыту, что 12 — это 4 × 3, а 8 — это 4 × 2. Машины, даже электронные, такие как компьютеры, не имеют этого преимущества — они не содержат справочного набора таблиц умножения, поэтому они должны делать это по-своему.
Каждый раз, когда мы сдвигаем нашу цифру один вправо, чтобы получить следующую цифру ответа, мы знаем, что сможем вычесть его либо ровно один раз, либо не вычесть вовсе. Нам только нужно выполнять одно вычитание за смену; недостатком является то, что, поскольку двоичные числа имеют много больше цифр, чем их десятичные эквиваленты, мы должны выполнить гораздо больше сдвигов.
MOV R1, # 128
MOV R0, R1, LSR # 2; смена R1 2 разряда
;Направо &
; хранить в R0
; ответьте сейчас в R0
Поскольку 4 равно 2 × 2, все, что нам нужно сделать, чтобы разделить на 4 в двоичном формате, — это сдвинуть регистр на два. местами вправо, так же как все, что нам нужно сделать, чтобы разделить на 100 (10 × 10) в десятичной дроби, это сдвинуть на два места вправо — например, от 600 пенсов получаем 6 фунтов.
Чтобы разделить 50 (% 110010) на 10 (% 1010) в двоичном формате:
Наша цифра «10» теперь сдвинута на две позиции вправо, возвращая ее к исходному значению, что является нашим сигналом к остановке и подсчету цифр в нашем ответе -% 101 в двоичном формате или «5» в десятичном, w ich — это, конечно, правильный ответ.
CMP R2, # 0 BEQ Divide_end ; проверьте деление на ноль!
MOV R0, # 0; очистить R0 для накопления результата
MOV R3, # 1; установить бит 0 в R3, который будет
; сдвинут влево, затем вправо
.Начало
CMP R2, R1
MOVLS R2, R2, LSL №1
MOVLS R3, R3, LSL # 1
BLS начало
; сдвиньте R2 влево, пока
; быть больше R1
; сдвиньте R3 влево параллельно по порядку
; чтобы отметить, как далеко нам нужно пройти
R0 будет использоваться для хранения результата. Роль R3 более сложная.
Фактически, мы используем R3, чтобы отметить, где должен находиться правый конец R2 — если мы сдвинем R2 осталось три места, это будет обозначено значением% 1000 в R3.Однако мы также добавляем его в R0 каждый раз, когда нам удается успешно вычитать, так как он отмечает позицию цифры в настоящее время рассчитывается в ответе. В приведенном выше двоичном примере (50 ÷ 10) мы сдвинул «10» на два места влево, поэтому во время первого вычитания R3 был бы % 100, во время второго (неудачного) было бы% 10, а во время третий% 1. Добавление его к R0 после каждого успешного вычитания снова дало бы нам ответ% 101!
Код ARM не имеет конкретных инструкций сдвига и поворота, присутствующих в не-RISC наборы инструкций.Вместо этого у него есть концепция «барреля-переключателя», который можно использовать для изменить значение, указанное в правом регистре для почти любой инструкции , без изменения самого регистра. Например, инструкция ADD R0, R1, R2, LSL # 2 будет сложите R1 и (R2 << 2) и загрузите результат в R0, не влияя на значение R2 никак. Это может быть очень полезно, но это означает, что если мы действительно хотим изменить значение R2, сдвигая его, как мы это делаем здесь, мы должны прибегнуть к перемещению его в себя через Переключатель: MOV R2, R2, LSL # 1.
.следующий
CMP R1, R2; перенос установлен, если R1> R2 (не спрашивайте почему)
SUBCS R1, R1, R2; вычтите R2 из R1, если это
; дать положительный ответ
ADDCS R0, R0, R3; и добавить текущий бит в R3 к
; накапливающийся ответ в R0
При вычитании кода ARM (инструкция CMP имитирует вычитание для установки флагов), если R1 — R2 дает положительный ответ и «заимствование» не требуется, флаг переноса равен и установлен .Это необходимо для правильной работы SBC (вычитание с переносом) при использовании для переноски. получается 64-битное вычитание, но это сбивает с толку!
В данном случае мы используем это в своих интересах. Флаг переноса устанавливается, чтобы указать, что возможно успешное вычитание, т. е. такое, которое не дает отрицательного результата, и две следующие инструкции выполняются только при выполнении условия Carry Set. Обратите внимание, что ‘S’ в конце этих инструкций является частью кода условия ‘CS’ и означает , а не . значит, что они устанавливают флаги!
MOVS R3, R3, LSR # 1; Сдвинуть R3 вправо во флаг переноса
MOVCC R2, R2, LSR # 1; и если бит 0 R3 был равен нулю, также
; сдвинуть R2 вправо
BCC следующий; если перенос не очищен, R3 сдвинулся
; назад туда, где все началось, и мы
; может закончиться
.Divide_end
MOV R25, R24; выход из программы
Следующие две инструкции сдвигают вправо R3, регистр «счетчик», и R2, который содержит число, на которое мы делим. Мы специально устанавливаем флаги, используя суффикс «S» при переключении R3, поскольку мы хотим знать, когда бит, хранящийся в этом регистре, достигает правой части. В течение сдвиг вправо, бит 0 передается во флаг переноса, в то время как остальные биты перемещаются вдоль. Поскольку установлен только один бит R3 (изначально он был загружен с% 1 перед сдвигом) влево, а затем вправо), когда установлен флаг переноса, он указывает, что перед сдвигом значение R3 было% 1, т.е.е. мы вернулись туда, откуда начали, и теперь R0 должен держать правую отвечать.
Как и в случае с результатами целочисленного деления в Basic, значение в R0 всегда будет округляться до next наименьшее целое число , а не до ближайшего числа.Например, 1156 ÷ 19 дает результат «60 остатков 16», который на самом деле ближе к 61, чем к 60.
Если ваша микросхема AVR поддерживает команду умножения (MUL), то умножение двух восьмибитных цифры довольно просты. MUL будет работать со всеми 32 регистрами с R0 по R31 и оставит младший байт результата в R0 и старшего байта в R1. Регистры множимого и множителя остаются без изменений. Процедура занимает около трех циклов.
.DEF ANSL = R0; Удерживать младший байт ответа
.DEF ANSH = R1; Хранить старший байт ответа
.DEF A = R16; удерживать множимое
.DEF B = R18; Удерживать множитель
LDI A, 42; Загрузить множимое в A
LDI B, 10; Загрузить множитель в B
MUL A, B; умножить содержимое A и B
; Результат 420 остался в ANSL и ANSH
Если наш AVR не поддерживает аппаратную команду MUL, нам придется вычислять умножение вручную. Если нам нужно умножить на степень двойки, например 2,4,8 и т. Д.Результат можно получить, сдвинув биты влево. Каждый сдвиг влево — это умножение на два.
Команда логического сдвига влево (LSL) используется для младшего байта, потому что она сдвиньте содержимое на один бит влево, ноль сдвинется в младший бит и самый старший бит сдвигается во флаг переноса.
10101010 Перенести [1] <- 01010100 <- 0 (LSL)
Мы используем команду «Повернуть влево, хотя переносить» (ROL) на старший байт, потому что она также сдвинет содержимое на один бит влево, но это переместит содержимое флага переноса в самый младший бит.
00000000 Перенести [0] <- 00000001 <- [1] Перенести (ROL)
Каждый раз, когда мы сдвигаем множимое влево, мы умножаем его на два. Итак, чтобы умножить на восемь, мы просто сдвигаем множимое влево три раза. Процедура занимает около десяти циклов.
.DEF ANSL = R0; Удерживать младший байт ответа
.DEF ANSH = R1; Хранить старший байт ответа
.DEF AL = R16; Для хранения младшего байта умножаемого
.DEF AH = R17; Для хранения старшего байта умножаемого
LDI AL, LOW (42); Загрузить множимое в AH: AL
LDI AH, ВЫСОКИЙ (42);
MUL8:
MOV ANSL, AL; Копировать множимое в R1: R0
MOV ANSH, AH;
LSL ANSL; Умножить на 2
ROL ANSH; Переместите Carry в R1
LSL ANSL; Умножить на 2x2 = 4
ROL ANSH; Переместите Carry в R1
LSL ANSL; Умножить на 2x2x2 = 8
РОЛ АНШ; Переместите переноску в R1
; Результат 42x8 = 336 осталось в ANSL и ANSH
Чтобы выполнить стандартное умножение, мы исследуем, как достигается двоичное умножение, мы замечаем, что когда цифра в множителе равна единице, мы добавляем сдвинутую версию множимое к нашему результату. Когда цифра множителя равна нулю, нам нужно добавить ноль, что означает, что мы ничего не делаем.
00101010 = 42 множимого
x00001010 = 10 множитель
--------
00000000
00101010
00000000
00101010
00000000
00000000
00000000
00000000
----------------
0000000110100100 = 420 результат
================
Приведенная ниже процедура имитирует аппаратное умножение (MUL), оставляя множимое и множитель не изменяется, и результат появляется в регистровой паре R1 и R0.Он сдвигает биты умножителя в бит переноса и использует содержимое переноса для сложите множимое, если оно равно единице, или пропустите его, если перенос равен нулю. Процедура занимает около шестидесяти циклов.
.DEF ANSL = R0; Удерживать младший байт ответа
.DEF ANSH = R1; Хранить старший байт ответа
.DEF A = R16; Для удержания множимого
.DEF B = R18; Удерживать множитель
.DEF C = R20; Удерживать битовый счетчик
LDI A, 42; Загрузить множимое в A
LDI B, 10; Загрузить множитель в B
MUL8x8:
LDI C, 8; Загрузить битовый счетчик в C
CLR ANSH; Очистить старший байт ответа
MOV ANSL, B; Копировать множитель в младший байт ответа
LSR ANSL; сдвинуть младший бит множителя в Carry
LOOP: BRCC SKIP; если перенос равен нулю, пропустить сложение
ADD ANSH, A; Сложить множимое для ответа
SKIP: ROR ANSH; сдвиг младшего бита старшего байта
ROR ANSL; ответа в младший байт
DEC C; Уменьшение битового счетчика
BRNE LOOP; Проверить, все ли восемь бит выполнены
; Результат 420 остался в ANSL и ANSH
Умножение двух 16-битных чисел может дать четырехбайтовый результат. Мы используем команду аппаратного умножения (MUL) для создания всех четырех перекрестных произведений. и добавьте их к 32-битному результату. Команда MUL оставляет свои результаты каждый раз в R1: R0, которые мы затем добавляем к нашему результату. Процедура занимает около двадцати циклов.
.DEF ZERO = R2; Удерживать ноль
.DEF AL = R16; Для удержания множимого
.DEF AH = R17
.DEF BL = R18; удерживать множитель
.DEF BH = R19
.DEF ANS1 = R20; Для хранения 32-битного ответа
.DEF ANS2 = R21
.DEF ANS3 = R22
.DEF ANS4 = R23
LDI AL, LOW (42); Загрузить множимое в AH: AL
LDI AH, ВЫСОКИЙ (42);
LDI BL, LOW (10); Загрузить множитель в BH: BL
LDI BH, ВЫСОКИЙ (10);
MUL16x16:
CLR ZERO; установить R2 в ноль
MUL AH, BH; Умножить старшие байты AHxBH
MOVW ANS4: ANS3, R1: R0; Переместить двухбайтовый результат в ответ
MUL AL, BL; Умножение младших байтов ALxBL
MOVW ANS2: ANS1, R1: R0; Переместить двухбайтовый результат в ответ
MUL AH, BL; Умножить AHxBL
ДОБАВИТЬ ANS2, R0; Добавить результат к ответу
АЦП ANS3, R1;
ADC ANS4, ZERO; добавить несущий бит
MUL BH, AL; Умножить BHxAL
ДОБАВИТЬ ANS2, R0; Добавить результат к ответу
АЦП ANS3, R1;
ADC ANS4, ZERO; добавить несущий бит
Умножение двухбайтовых чисел вместе может дать результат шириной четыре байта (32 бита). С помощью этой процедуры мы добавляем множимое к старшим байтам нашего результата для каждого, что появляется в нашем 16-битном умножителе, затем сдвинем результат в младшие байты нашего результата шестнадцать раз, один раз для каждого бита нашего множителя. Процедура занимает около 180 циклов.
.DEF AL = R16; Для удержания множимого
.DEF AH = R17
.DEF BL = R18; удерживать множитель
.DEF BH = R19
.DEF ANS1 = R20; Для хранения 32-битного ответа
.DEF ANS2 = R21
.DEF ANS3 = R22
.DEF ANS4 = R23
.DEF C = R24; Битовый счетчик
LDI AL, LOW (42); Загрузить множимое в AH: AL
LDI AH, ВЫСОКИЙ (42);
LDI BL, LOW (10); Загрузить множитель в BH: BL
LDI BH, ВЫСОКИЙ (10);
MUL16x16:
CLR ANS3; Обнулить старшие байты результата
CLR ANS4;
LDI C, 16; битовый счетчик
LOOP: LSR BH; множитель сдвига вправо
ROR BL; сдвинуть самый младший бит в флаг переноса
BRCC SKIP; если перенос равен нулю, пропустить добавление
ADD ANS3, AL; Добавить множимое в старшие байты
ADC ANS4, AH; результата
SKIP: ROR ANS4; Повернуть старшие байты результата в
ROR ANS3; младшие байты
ROR ANS2;
ROR ANS1;
DEC C; Проверить, все ли 16 бит обработаны
BRNE LOOP; Если нет, то вернитесь назад
Следующая процедура умножит два 32-битных числа на 64-битный (8-байтовый) результат. Процедура занимает около 500 тактов.
.DEF ANS1 = R0; 64-битный ответ
.DEF ANS2 = R1;
.DEF ANS3 = R2;
.DEF ANS4 = R3;
.DEF ANS5 = R4;
.DEF ANS6 = R5;
.DEF ANS7 = R6;
.DEF ANS8 = R7;
.DEF A1 = R16; Множаемое
.DEF A2 = R17;
.DEF A3 = R18;
.DEF A4 = R19;
.DEF B1 = R20; Множитель
.DEF B2 = R21;
.DEF B3 = R22;
.DEF B4 = R23;
.DEF C = R24; Счетчик циклов
LDI A1, НИЗКИЙ ($ FFFFFFFF)
LDI A2, BYTE2 ($ FFFFFFFF)
LDI A3, BYTE3 ($ FFFFFFFF)
LDI A4, BYTE4 ($ FFFFFFFF)
LDI B1, НИЗКИЙ ($ FFFFFFFF)
LDI B2, BYTE2 ($ FFFFFFFF)
LDI B3, BYTE3 ($ FFFFFFFF)
LDI B4, BYTE4 ($ FFFFFFFF)
MUL3232:
CLR ANS1; инициализировать ответ нулем
CLR ANS2;
CLR ANS3;
CLR ANS4;
CLR ANS5;
CLR ANS6;
CLR ANS7;
SUB ANS8, ANS8; очистить ANS8 и флаг переноса
MOV ANS1, B1; Копировать множитель для ответа
MOV ANS2, B2;
MOV ANS3, B3;
MOV ANS4, B4;
LDI C, 33; Установить счетчик циклов на 33
ПЕТЛЯ:
ROR ANS4; множитель сдвига вправо
ROR ANS3;
ROR ANS2;
ROR ANS1;
DEC C; счетчик цикла уменьшения
BREQ DONE; Проверить, все ли биты обработаны
BRCC SKIP; If Carry Clear пропустить добавление
ДОБАВИТЬ ANS5, A1; Добавить мультипис. В ответ
АЦП ANS6, A2;
АЦП ANS7, A3;
АЦП ANS8, A4;
ПРОПУСКАТЬ:
ROR ANS8; сдвиг старших байтов ответа
ROR ANS7;
ROR ANS6;
ROR ANS5;
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
Поскольку команды аппаратного разделения нет, нам придется делать это вручную. Если нам нужно разделить на степень двойки, например 2,4,8 и т. Д. Результат может быть достигнут сдвигом битов вправо. Каждый сдвиг вправо - это деление на два.
Команда логического сдвига вправо (LSR) используется для старшего байта, потому что она сдвигает содержимое на один бит вправо, ноль сдвигается в старший бит, а младший бит сдвигается во флаг переноса.
01010101
0 -> 00101010 -> [1] Перенести
Мы используем команду «Повернуть вправо, хотя переносить» (ROR) для младшего байта, потому что она также сдвинет содержимое на один бит вправо, но это переместит содержимое флага переноса в самый старший бит.
00000000 Перенести [1] -> 10000000 -> [0] Перенести (ROL)
Каждый раз, когда мы сдвигаем множимое вправо, мы делим его на два. Итак, чтобы разделить на восемь, мы просто сдвигаем множимое вправо три раза.Процедура занимает около десяти циклов.
.DEF ANSL = R0; Удерживать младший байт ответа
.DEF ANSH = R1; Хранить старший байт ответа
.DEF AL = R16; Для хранения младшего байта умножаемого
.DEF AH = R17; Для хранения старшего байта умножаемого
LDI AL, LOW (416); Загрузить множимое в A
LDI AH, ВЫСОКИЙ (416);
DIV8:
MOVW ANSH: ANSL, AH: AL; Копировать множимое в результат
ЛСР АНШ; Разделить на 2
ROR ANSL; Сдвинуть флаг переноса на R0
ЛСР АНШ; Разделить на 4 (2x2)
ROR ANSL; Сдвинуть флаг переноса в R0
ЛСР АНШ; Разделить на 8 (2x2x2)
ROR ANSL; Сдвинуть флаг переноса в R0
; Результат 416/8 = 52 осталось в ANSL и ANSH
Точно так же, как умножение может быть достигнуто с помощью сдвига и сложения. Деление можно осуществить сдвигом и вычитанием. Приведенная ниже процедура пытается многократно вычесть делитель. Если результат отрицательный, процесс отменяется, и дивиденды сдвигаются влево, чтобы повторить попытку. Процедура занимает около 90 циклов.
.DEF ANS = R0; Удерживать ответ
.DEF REM = R2; Для удержания остатка
.DEF A = R16; Держать дивиденды
.DEF B = R18; удерживать делитель
.DEF C = R20; Битовый счетчик
LDI A, 255; Загрузить делимое в A
LDI B, 5; Делитель нагрузки в B
DIV88:
LDI C, 9; счетчик битов загрузки
SUB REM, REM; Очистить остаток и перенести
MOV ANS, A; Копировать дивиденд в ответ
LOOP: ROL ANS; сдвиньте ответ влево
DEC C; счетчик уменьшения
BREQ DONE; выйти, если выполнено восемь бит
ROL REM; сдвинуть остаток влево
SUB REM, B; Попробуйте вычесть делитель из остатка
BRCC SKIP; Если результат отрицательный, то
ADD REM, B; обратное вычитание, чтобы повторить попытку
CLC; Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP; обратная петля
SKIP: SEC; Установить флаг переноса на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
Предыдущая подпрограмма может быть расширена для обработки двухбайтовых чисел в диапазоне от нуля до 65 535. Процедура занимает около 230 циклов.
.DEF ANSL = R0; Удерживать младший байт ответа
.DEF ANSH = R1; Хранить старший байт ответа
.DEF REML = R2; Для хранения младшего байта остатка
.DEF REMH = R3; Для хранения старшего байта остатка
.DEF AL = R16; Для хранения младшего байта дивиденда
.DEF AH = R17; Хранить старший байт дивиденда
.DEF BL = R18; Для хранения младшего байта делителя
.DEF BH = R19; Для хранения старшего байта делителя
.DEF C = R20; Битовый счетчик
LDI AL, LOW (420); Загрузить младший байт делимого в AL
LDI AH, HIGH (420); Загрузить старший байт делимого в AH
LDI BL, LOW (10); Загрузить младший байт делителя в BL
LDI BH, HIGH (10); Загрузить старший байт делителя в BH
DIV1616:
MOVW ANSH: ANSL, AH: AL; Скопировать делимое в ответ
LDI C, 17; битовый счетчик нагрузки
SUB REML, REML; очистить остаток и перенести
CLR REMH;
LOOP: ROL ANSL; сдвиньте ответ влево
РОЛ АНШ;
DEC C; счетчик уменьшения
BREQ DONE; выйти, если выполнено шестнадцать бит
ROL REML; Сдвинуть остаток влево
ROL REMH;
SUB REML, BL; Попробуйте вычесть делитель из остатка
SBC REMH, BH
BRCC SKIP; Если результат отрицательный, то
ADD REML, BL; отмените вычитание, чтобы повторить попытку
ADC REMH, BH;
CLC; Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP; обратная петля
SKIP: SEC; Установить флаг переноса на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
Предыдущая подпрограмма может быть расширена для обработки 32-битного числа, деленного на 16-битное число, Это означает, что числа в диапазоне от нуля до 4 294 967 295 (4,3 миллиарда) разделены на числа в диапазоне от нуля до 65 535. Процедура занимает около 700 циклов.
.DEF ANS1 = R0; Удерживать младший байт ответа
.DEF ANS2 = R1; Для хранения второго байта ответа
.DEF ANS3 = R2; Для хранения третьего байта ответа
.DEF ANS4 = R3; Для хранения четвертого байта ответа
.DEF REM1 = R4; для хранения первого байта остатка
.DEF REM2 = R5; Для хранения второго байта остатка
.DEF REM3 = R6; Для хранения третьего байта остатка
.DEF REM4 = R7; Для хранения четвертого байта остатка
.DEF ZERO = R8; Удерживать нулевое значение
.DEF A1 = R16; Для хранения младшего байта дивиденда
.DEF A2 = R17; Для хранения второго байта делимого
.DEF A3 = R18; Для хранения третьего байта дивиденда
.DEF A4 = R19; Для хранения четвертого байта делимого
.DEF BL = R20; Для хранения младшего байта делителя
.DEF BH = R21; Для хранения старшего байта делителя
.DEF C = R22; Битовый счетчик
LDI A1, LOW (420); Загрузить младший байт делимого в A1
LDI A2, BYTE2 (420); Загрузить второй байт делимого в A2
LDI A3, BYTE3 (420); Загрузить третий байт делимого в A3
LDI A4, BYTE4 (420); загрузить четвертый байт делимого в A4
LDI BL, LOW (10); Загрузить младший байт делителя в BL
LDI BH, HIGH (10); Загрузить старший байт делителя в BH
DIV3216:
CLR ZERO
MOVW ANS2: ANS1, A2: A1; Скопировать делимое в ответ
MOVW ANS4: ANS3, A4: A3;
LDI C, 33; битовый счетчик нагрузки
SUB REM1, REM1; очистить остаток и перенести
CLR REM2;
CLR REM3;
CLR REM4;
LOOP: ROL ANS1; сдвиньте ответ влево
ROL ANS2;
ROL ANS3;
ROL ANS4;
DEC C; счетчик уменьшения
BREQ DONE; выйти, если выполнено 32 бита
ROL REM1; Сдвинуть остаток влево
ROL REM2;
ROL REM3;
ROL REM4;
SUB REM1, BL; Попробуйте вычесть делитель из остатка
SBC REM2, BH;
SBC REM3, ZERO;
SBC REM4, ZERO;
BRCC SKIP; Если результат отрицательный, то
ADD REM1, BL; отмените вычитание, чтобы повторить попытку
ADC REM2, BH;
АЦП REM3, НУЛЬ;
АЦП REM4, НУЛЬ;
CLC; Очистить флаг переноса, чтобы ноль сместился в A
RJMP LOOP; обратная петля
SKIP: SEC; Установить флаг переноса на A
ПЕТЛЯ RJMP
ВЫПОЛНЕНО:
Если мы изучим приведенную выше таблицу, то заметим, что квадратный корень из числа равен количество суммированных нечетных чисел. Мы просто создаем процедуру, которая отслеживает общее количество вычтенных нечетных чисел. Процедура занимает от пятнадцати до ста циклов.
.DEF ANS = R0; Удерживать ответ .DEF A = R16; Удерживать квадрат .DEF B = R18; Сумма, Рабочее пространство. LDI A, 100; Загрузите квадрат в A КОРЕНЬ: ПЕТЛЯ: SUB A, B; вычесть B из квадрата BRCS DONE; Если больше, чем sqaure, мы закончили INC ANS; Увеличить ответ SUBI B, -2; Приращение B на два ПЕТЛЯ RJMP
Мы могли бы расширить описанную выше процедуру для обработки квадратного корня из шестнадцатибитного числа. но количество тактовых циклов может достигать 3750. Приведенная ниже процедура обрабатывает два бита за раз, начиная с самых высоких битов и также предоставляет остаток. Он использует около 160 тактов.
.DEF ANSL = R0; Квадратный корень (ответ)
.DEF ANSH = R1;
.DEF REML = R2; Остаток
.DEF REMH = R3;
.DEF AL = R16; Квадрат для укоренения (ввод)
.DEF AH = R17;
.DEF C = R20; Счетчик циклов
LDI AL, НИЗКИЙ ($ FFFF)
LDI AH, ВЫСОКИЙ ($ FFFF)
SQRT16:
PUSH AL; Сохранить площадь для последующего восстановления
PUSH AH;
CLR REML; инициализировать остаток до нуля
CLR REMH;
CLR ANSL; Инициализировать корень до нуля
CLR ANSH;
LDI C, 8; установить счетчик циклов на восемь
ПЕТЛЯ:
LSL ANSL; Умножить корень на два
РОЛ АНШ;
LSL AL; сдвиг на два старших бита квадрата
ROL AH; в остаток
ROL REML;
ROL REMH;
LSL AL; сдвиг второго старшего бита Sqaure
ROL AH; в остаток
ROL REML;
ROL REMH;
CP ANSL, REML; Сравнить корень с остатком
CPC ANSH, REMH;
BRCC SKIP; если остаток меньше или равен корневому
INC ANSL; Приращение корня
SUB REML, ANSL; вычесть корень из остатка
SBC REMH, ANSH;
INC ANSL; Приращение корня
ПРОПУСКАТЬ:
DEC C; счетчик цикла уменьшения
BRNE LOOP; Проверить, все ли биты обработаны
LSR ANSH; Разделить корень на два
ROR ANSL;
POP AH; Восстановить исходную площадь
ПОП АЛЬ
ПЕТЛЯ RJMP
Мы можем расширить предыдущую процедуру для обработки 32-битных чисел. Для завершения требуется от 500 до 580 тактов.
.DEF ANS1 = R0; Квадратный корень (ответ)
.DEF ANS2 = R1;
.DEF ANS3 = R2;
.DEF ANS4 = R3;
.DEF REM1 = R4; Остаток
.DEF REM2 = R5;
.DEF REM3 = R6;
.DEF REM4 = R7;
.DEF A1 = R16; Квадрат (ввод)
.DEF A2 = R17;
.DEF A3 = R18;
.DEF A4 = R19;
.DEF C = R20; Счетчик циклов
LDI A1, НИЗКИЙ ($ FFFFFFFF)
LDI A2, BYTE2 ($ FFFFFFFF)
LDI A3, BYTE3 ($ FFFFFFFF)
LDI A4, BYTE4 ($ FFFFFFFF)
sqrt16:
НАЖМИТЕ A1; Сохранить квадрат для последующего восстановления
PUSH A2;
НАЖАТЬ A3;
PUSH A4;
CLR REM1; инициализировать остаток до нуля
CLR REM2;
CLR REM3;
CLR REM4;
CLR ANS1; инициализировать корень до нуля
CLR ANS2;
CLR ANS3;
CLR ANS4;
LDI C, 16; Установить счетчик циклов на шестнадцать
ПЕТЛЯ:
LSL ANS1; Умножить корень на два
ROL ANS2;
ROL ANS3;
ROL ANS4;
LSL A1; сдвиг на два старших бита квадрата
ROL A2; в остаток
ROL A3;
ROL A4;
ROL REM1;
ROL REM2;
ROL REM3;
ROL REM3;
LSL A1; сдвиг второго старшего бита Sqaure
ROL A2; в остаток
ROL A3;
ROL A4;
ROL REM1;
ROL REM2;
ROL REM3;
ROL REM4;
CP ANS1, REM1; Сравнить корень с остатком
КТК ANS2, REM2;
КТК ANS3, REM3;
КТК ANS4, REM4;
BRCC SKIP; если остаток меньше или равен корневому
INC ANS1; Увеличение корня
SUB REM1, ANS1; вычесть корень из остатка
SBC REM2, ANS2;
SBC REM3, ANS3;
SBC REM4, ANS4;
INC ANS1; Увеличение корня
ПРОПУСКАТЬ:
DEC C; счетчик цикла уменьшения
BRNE LOOP; Проверить, все ли биты обработаны
LSR ANS4; Разделить корень на два
ROR ANS3;
ROR ANS2;
ROR ANS1;
POP A4; Восстановить исходную площадь
POP A3
POP A2
POP A1
Команды M (RX) и MR (RR) выполняют умножение двоичных полных слов операндов.Инструкции умножения использовать четно-нечетную регистровую пару для хранения первого операнда и продукта. Пара четно-нечетных регистров пара последовательных регистров, которая начинается с четного регистра, например регистры 2 и 3, регистры 6 и 7 или регистры 10 и 11.
Чтобы произвести умножение, множимое загружается в нечетный регистр четно-нечетной пары. Чётный регистр — это один, указанный в инструкции умножения. После умножения продукт находится в четно-нечетной паре.Если вы знаете, что продукт подойдет один регистр, тогда он будет в нечетном регистре пары.Команды D (RX) и DR (RR) выполняют деление двоичных полных слов операндов. В инструкциях по разделению используется четно-нечетная регистровая пара для хранения первого операнда, частного и остатка.
Для выполнения деления делимое загружается в нечетный регистр четно-нечетной пары. Чётный регистр также должен быть инициализирован; если дивиденд положительный, в четном регистре должны быть установлены двоичные нули, и если делимое отрицательное значение, четный регистр должен быть установлен в двоичном формате.В стандартный способ сделать это — загрузить дивиденд, а затем умножить его на один, чтобы сделать делимое 8-байтовым числом. Чётный регистр — это один, упомянутый в инструкции разделения. После разделения нечетный регистр содержит частное, а четный регистр содержит остаток.
| Версия C ++ | Версия ассемблера |
|---|---|
| А = В * С; | L 5, B M 4, C ST 5, A |
| А = В * С; | L 7, B L 11, C MR 6,11 ST 7, A |
| А = В / С; | L 7, B M 6, = F’1 ‘ D 6, C ST 7, A |
| А = В / С; | L 11, B L 3, C M 10, = F’1 ‘ DR 10,3 ST 11, A |
| A = B% C; | L 3, B M 2, = F’1 ‘ D 2, C ST 2, A |
| A = B% C; | L 9, B L 7, C M 8, = F’1 ‘ DR 8,7 ST 8, A |
Напишите мне | Часы работы офиса | Моя домашняя страница | Департамент Главная | Домашняя страница MCC
© Авторское право Emmi Schatz 2003
В этой главе описывается стандартное умножение целых чисел и расширение инструкции деления, которое называется «M» и содержит инструкции, которые умножают или делят значения, содержащиеся в двух целых числах регистры.
MUL выполняет умножение XLEN-бит × XLEN-бит RS1 на RS2 и размещает младшие биты XLEN в регистре назначения. МУЛ, МУЛХУ и МУЛХУ выполнить то же умножение, но вернуть старшие биты XLEN полный 2 × XLEN-битный продукт, для подписанных × подписанных, беззнаковый × беззнаковый и подписанный rs1 × беззнаковый rs2 умножение, соответственно. Если старшие и младшие биты одного и того же продукта равны требуется, то рекомендуемая кодовая последовательность: MULH [[S] U] rdh, RS1, RS2 ; MUL rdl, rs1, rs2 (спецификаторы регистра источника должны быть в том же порядке и rdh не может быть таким же, как rs1 или RS2 ).Микроархитектуры могут затем объединить их в единое целое. операция умножения вместо выполнения двух отдельных операций умножения.
MULW — это инструкция RV64, которая умножает младшие 32 бита источника. регистры, помещая знаковое расширение младших 32 бит результата в регистр назначения.
DIV и DIVU выполняют биты XLEN на биты XLEN целое число со знаком и без знака деление RS1 на RS2 с округлением до нуля.REM и REMU обеспечивают оставшуюся часть соответствующей операции деления. Для REM знак результата равен знаку дивиденда.
Если и частное, и остаток требуются из того же подразделения, рекомендуемая кодовая последовательность: DIV [U] rdq, RS1, RS2 ; REM [U] rdr, rs1, rs2 ( rdq не может быть таким же, как RS1 или RS2 ). Микроархитектуры могут затем объедините их в одну операцию разделения вместо выполнения два отдельных дивизиона.
DIVW и DIVUW — это инструкции RV64, которые делят младшие 32 бита RS1 младшими 32 битами RS2 , обрабатывая их как целые числа со знаком и без знака соответственно, помещая 32-битный частное в rd , расширенное знаком до 64 бит. REMW и REMUW инструкции RV64, которые предоставляют соответствующие знаковые и беззнаковые операции остатка соответственно. И REMW, и REMUW всегда расширяет 32-битный результат до 64 бит, в том числе на делим на ноль.
Семантика деления на ноль и переполнения при делении кратко изложена в Таблица [вкладка: divby0]. Для частного деления на ноль установлены все биты, и остаток от деления на ноль равен дивиденду. Переполнение подписанного деления происходит только тогда, когда самое отрицательное целое число делится на — 1. Частное от знаковое деление с переполнением равно дивиденду, а остаток равен нуль. Переполнение беззнакового деления не может произойти.
| Деление на ноль | x | 0 | 2 L — 1 | x | — 1 | x |
| Переполнение (только с подписью) | — 2 L — 1 | — 1 | – | – | — 2 L — 1 | 0 |
С возвращением,
Прежде чем мы начнем, я хочу сказать вам, что мы используем библиотеки Irvine и процессор 86x для выполнения таких операций, как упомянуто выше!
Я использую Irvine Library в Visual Studio 2010 Professional для запуска ассемблера для выполнения моего кода!
ДЛЯ ЛУЧШЕГО ПОНИМАНИЯ:
«Процессор имеет только регистрацию в использовании i.е. eax , который используется для отображения, чтобы вы могли хранить данные в других регистрах, но не забудьте поместить свой окончательный результат в регистр eax , чтобы ваша программа не содержала ошибок, вся эта игра сборки передает значения в свободный регистр и правый регистр, где eax — аккумулятор «
»Предположим, значение: 8 + 2 => 10
Предположим, значение: 8-2 => 10
Предположим, значение: 8 * 2 => 10
Сложение + умножение и деление вместе, фокус «ПРОХОДНЫЕ ЗНАЧЕНИЯ»
Предположим, уравнение: (3 * 4) + (6/2) + (5 * 2) = 25
.mov 3 в eax и mov 4 в ebx и используйте mul ebx, чтобы поместить 12 в eax
теперь переместите eax в ecx, как показано в коде!
mov 6 в eax и mov 2 в ebx и div ebx, чтобы поместить ответ в eax
теперь используйте add ecx, eax означает, что ответ 3 * 4 + 6/2 находится в регистре ecx
eax свободен, теперь поместите 5 в eax и снова 2 в ebx!
снова используйте mul ebx и добавьте eax, равный 5 * 2 = 10, в ecx, чтобы получить ответ, равный 25!
.