8-900-374-94-44
| Библиотека: | Базовые |
| Введён в: | 2.0 Beta 1 для Исключающее ИЛИ/Нечётность/Чётность; 2.0 Beta 6 для Исключающее ИЛИ-НЕ |
| Внешний вид: |
Элементы Исключающее ИЛИ, Исключающее ИЛИ-НЕ, Нечётность и Чётность вычисляют соответствующую функцию от значений на входах и выдают результат на выход.
По умолчанию, неподключенные входы игнорируются — то есть, если входы действительно не имеют ничего подключенного к ним — даже провода. Таким образом, вы можете добавить 5-входовый элемент, но подключить только два входа, и он будет работать как 2-входовый элемент; это избавляет вас от необходимости беспокоиться о настройке количества входов каждый раз при создании элемента. (Если все входы не подключены, то на выходе значение ошибки X.
Ошибка для неопределённых входовдля
Выход элемента при неопределённости.
Двухвходовая таблица истинности для элементов следующая.
| x | y | Исключающее ИЛИ | Исключающее ИЛИ-НЕ | Нечётность | Чётность |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Как вы можете видеть, элементы Нечётность и Исключающее ИЛИ ведут себя одинаково в случае двух входов; аналогично, элементы Чётность и Исключающее ИЛИ-НЕ ведут себя одинаково.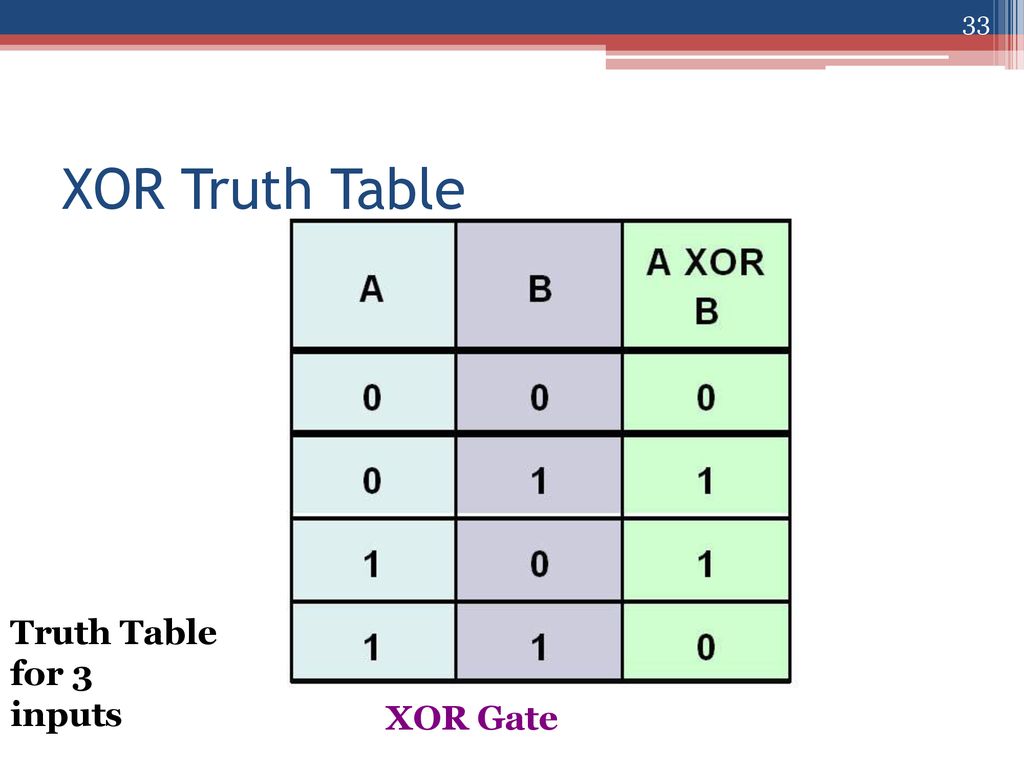
Но если входов с определённым значением больше двух, то элемент Исключающее ИЛИ будет давать на выходе 1, когда единица строго на одном входе, тогда как элемент Нечётность даст на выходе 1, когда единица на нечётном количестве входов. Элемент Исключающее ИЛИ-НЕ будет давать на выходе 1, когда входов с единицей строго не один, тогда как элемент Чётность даст 1, когда входов с единицей чётное количество. Элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ имеют атрибут, названный Многовходовое поведение, который позволяет настроить их на использование поведения элементов Нечётность и Чётность.
Если на каких-либо входах значение ошибки (например, если противоречивые значения поступают на один и тот же провод) или плавающее значение, то на выходе будет значение ошибки.
Многобитные версии каждого элемента будут выполнять свои однобитные преобразования над входами поразрядно.
Примечание: многие специалисты утверждают, что поведение фигурного элемента Исключающее ИЛИ должно соответствовать поведению элемента Нечётность, но по этому вопросу нет согласия.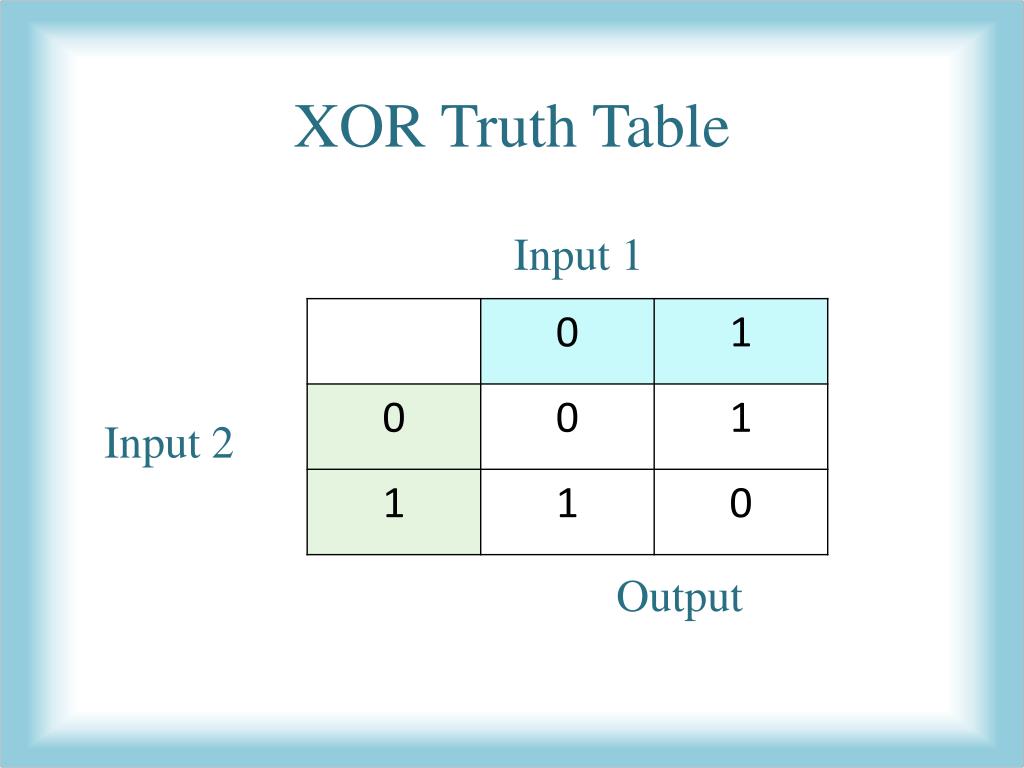
Поведение Logisim по умолчанию для элемента Исключающее ИЛИ основано на стандарте IEEE 91. Это также согласуется с интуитивным пониманием термина Исключающее ИЛИ: официант, спрашивающий, хотите вы гарнир из картофельного пюре, моркови, зеленого горошка, или шинкованной капусты, примет только один выбор, а не три, независимо от того, что вам могут сказать некоторые специалисты. (Должен признать, однако, что я не подвергал это заявление серьезным испытаниям.) Вы можете настроить элементы Исключающее ИЛИ и Исключающее ИЛИ-НЕ на использование одного из вариантов, меняя его атрибут Многовходовое поведение
.
Входы компонента. Их будет столько, сколько указано в атрибуте Количество входов.
Заметьте, что если вы используете фигурные элементы, то западный край элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет искривлён.
Тем не менее, входные контакты расположены вряд. Logisim отрисовывает короткие отрезки чтобы показать это; если вы перекроете отрезок, программа будет без предупреждений предполагать, что вы не хотели перекрыть его. При использовании «Вида для печати», эти отрезки не будут отрисованы, если не подключены к проводам.
Выход элемента, значение на котором вычисляется на основании текущих значений на входах, как описано выше.
Когда компонент выбран, или уже добавлен, клавиши от 0 до 9 меняют его атрибут Количество входов
, комбинации от Alt-0 до Alt-9 меняют его атрибут Биты данных
, а клавиши со стрелками меняют его атрибут Направление
.
Нет.
Нет.
Назад к Справке по библиотеке
Я знаю, что оператор XOR в базе 2 для двух битов A и B равен (A + B)% 2.
Если я хочу вычислить таблицу истинности для операции XOR в троичной системе (база 3), это то же самое, что и сложение по модулю 3? Например: в системе base 3 2 XOR 2 = 1 (так как (2 + 2)% 3 = 1)?
Я прочитал эту ссылку, в которой указано, что 2 XOR 2 в базовой системе 3 равно 2, и я не могу понять формулу этого?
Вообще, для любой базы ‘x’, является ли операция XOR для этой базы — сложением по модулю x?
2
Bugaboo 5 Мар 2017 в 02:27
Лучший ответ
Что ж, XOR означает e X кластер ИЛИ , и это логическая операция. И эта операция определяется только в двоичной логике. В вашей ссылке автор определяет совершенно другой оператор, который работает так же, как XOR для двоичной базы.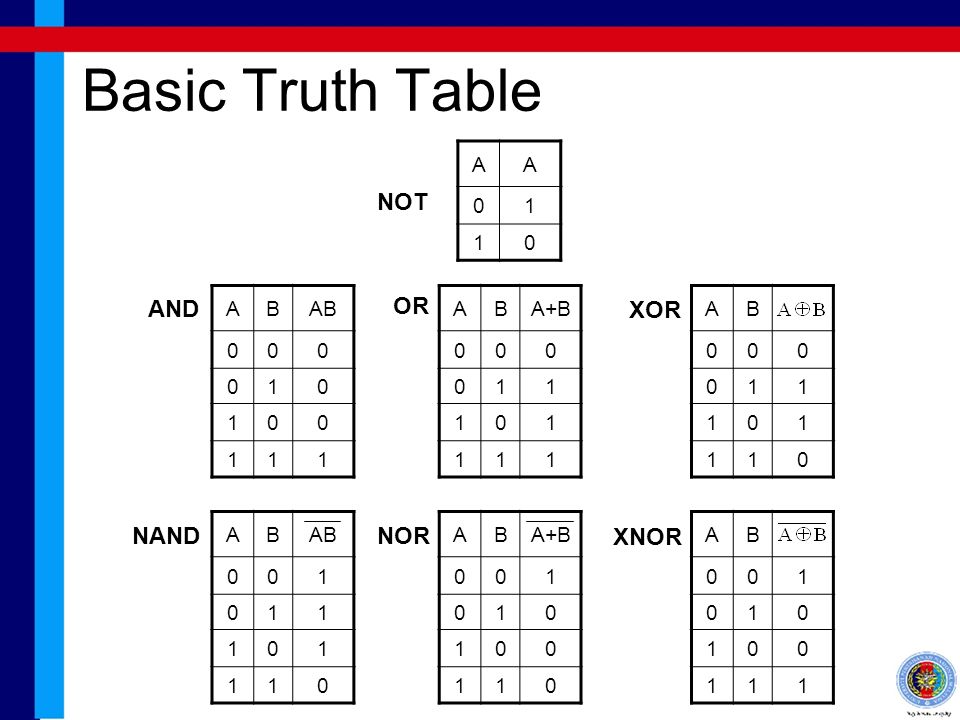
A ⊕ b = (a + b) мод 2
В этом случае ваш «расширенный XOR» для базы 3 будет производить вывод 1 для входов 2, 2. Но этот XOR3 больше не будет удовлетворять другим уравнениям, которые работают для стандартного XOR, например, вот эти:
A ⊕ b ⊕ b = a
A ⊕ b ⊕ a = b
Если вы решите «сохранить» их, вы получите операцию по вашей ссылке. Вы также можете сохранить некоторые другие свойства XOR, скажем,
A ⊕ a = 0
И получить другую операцию, которая отличается от первых двух.
Итак, короткий ответ: фраза «XOR-функция для недвоичных оснований» не имеет никакого смысла. Оператор XOR определяется только в двоичной логике. Если вы хотите расширить его для недвоичных оснований или нецелых чисел или комплексных чисел или чего-либо еще, вы можете сделать это и определить некоторую функцию расширения с любым поведением и любой «таблицей истинности», которую вы хотите.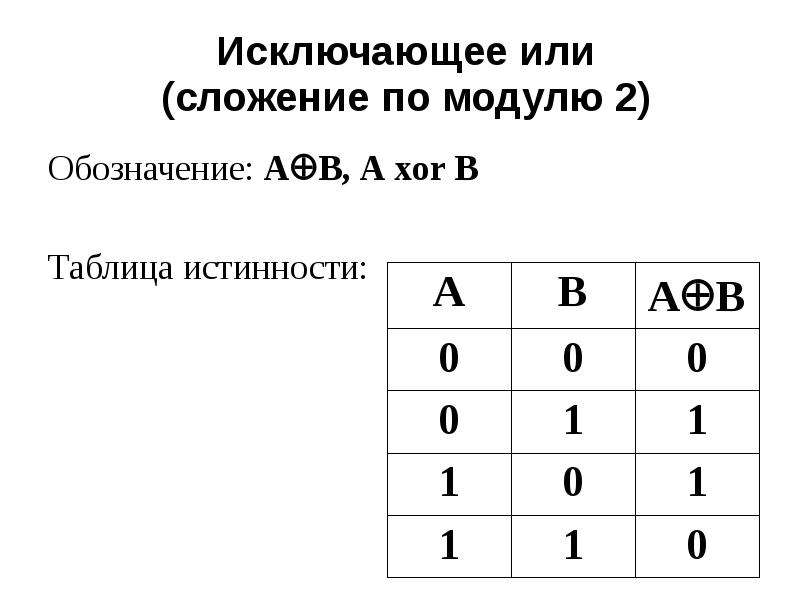
Но это расширение больше не будет функцией XOR.
1
Dim_ov 5 Мар 2017 в 00:18
Хотя я не знаю, что XOR технически был определен в более высоких основаниях, свойства XOR могут поддерживаться в более высоких основаниях, так что:
A ⊕ b ⊕ b = a
A ⊕ b ⊕ a = b
Как показывает сообщение в блоге, использование (base - (a + b) % base) % base работает. Часть, которую вы пропустили, является первым экземпляром base . В примере 2 ⊕ 2 в базе 3 мы получаем (3 - (2 + 2) % 3) % 3), который дает 2. Эта формула работает только с однозначными числами. Если вы хотите расширить до нескольких цифр, вы должны использовать одну и ту же формулу с каждой парой цифр, точно так же, как стандартный двоичный код XOR делает это поразрядно.
Например, 185 × 42 в базе 10 при запуске для каждой пары цифр (то есть сотен, десятков, единиц) дает нам:
(10 - (1 + 0) % 10) % 10 => 9
(10 - (8 + 4) % 10) % 10 => 8
(10 - (5 + 2) % 10) % 10 => 3
Или 983, когда вместе взятые.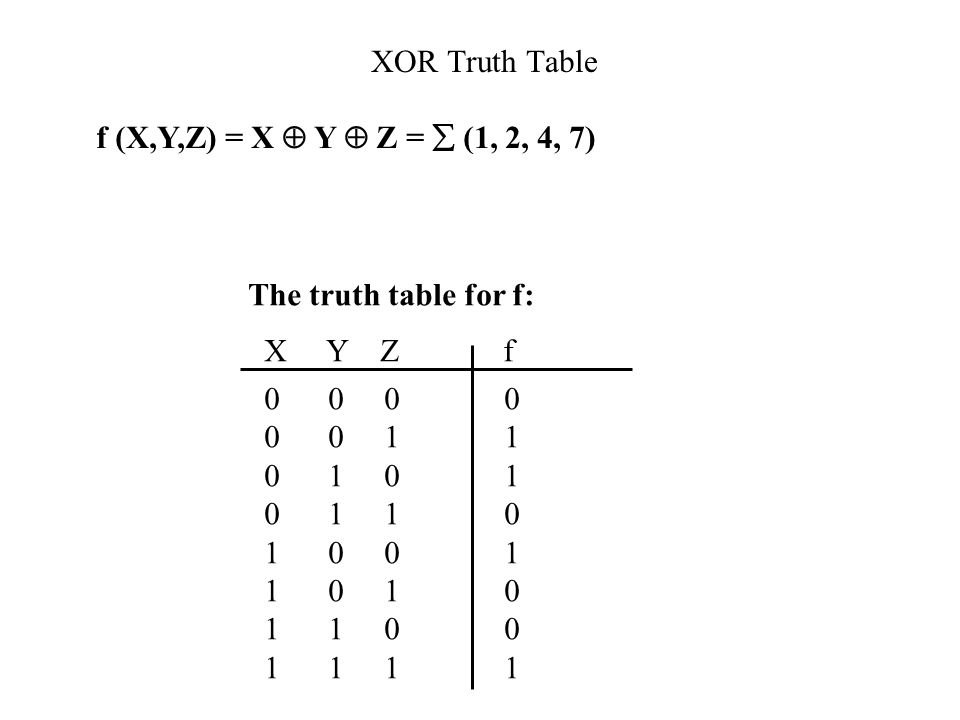
1
Sean 11 Сен 2019 в 17:11
Доступно с лицензией Image Analyst.
Доступно с лицензией Spatial Analyst.
Для выполнения этой функции необходимо наличие двух входных значений.
Порядок входных данных не имеет значения для этой функции.
Если входной тип данных – это значения с плавающей точкой, значения преобразуются в целые числа путем округления до выполнения побитовой операции.
У всех побитовых операций есть общие особенности:
Если целое число положительное, битовая позиция равна нулю; если оно отрицательное, битовая позиция равна единице.Операция побитового XOr обрабатывает знаковый разряд как и любой другой бит. Если одно или оба входных значения в местоположении пиксела отрицательные, выходное значение отрицательное; если оба входных значения положительные, выходное значение положительное.
Если оба входных растра являются одноканальными или на входе имеется константа, на выходе получится одноканальный растр.
Если оба входных растра являются многоканальными или на входе есть константа, выходной растр будет многоканальным. Количество каналов в каждом входном многоканальном растре должно быть одинаковым.
Функция будет выполнять операцию для каждого канала одного растра и соответствующего канала другого растра. Если один из входных растров является многоканальным, а другие входные данные — константа, функция выполнит операцию с постоянным значением для каждого канала многоканального входного растра.
Побитовые инструменты оценивают бинарные представления входных значений по принципу пиксел-за-пикселом. Для каждого бита в побитовом представлении выполняется булева операция.
Логика работы различных побитовых инструментов показана в следующих сценариях. Стрелки используются для обозначения хода операции конвертации входных значений в бинарные представления по основанию 2, анализа и возвращения результата в виде десятичных 10) значений.
Для функции Xor (побитовый) для каждого бита, где одно входное значение 1, а другое 0, выходное значение равно 1. Если оба бита равны 1 или оба равны 0, выходным значением бита будет 0.
Пример побитовых операторов , And, Or и Xor .
Оператором называется знак или символ, указывающий на тип вычислений, которые выполняются в выражении.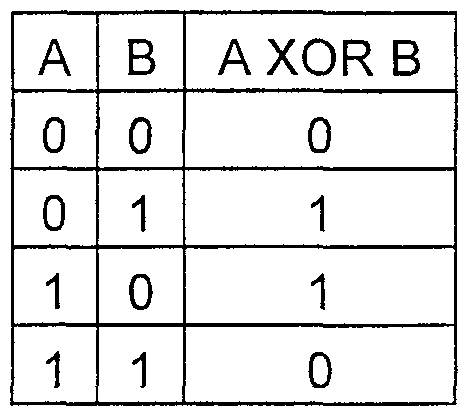
Существуют математические, логические операторы, а также операторы сравнения и ссылок. Access поддерживает различные операторы, включая арифметические операторы, такие как +, —, умножение (*) и деление (/), а также операторы для сравнения значений, текстовые операторы для сцепления текста и логические операторы для определения значений «Истина» и «Ложь». Эта статья содержит сведения об использовании таких операторов.
Примечание: В Access 2010 и более поздних версий построитель выражений включает функцию IntelliSense, которая указывает требуемые аргументы.
|
Арифметические операторы используется для вычисления значения на основе нескольких чисел или изменения знака числа из положительного в отрицательный и наоборот.
|
К началу страницы
Операторы сравнения позволяют сравнивать значения. Они возвращают результат «Истина», «Ложь» или Null.
Оператор | Назначение | Пример |
|---|---|---|
|
< |
Возвращает значение «Истина», если первое значение меньше второго. |
значение1 < значение2 |
|
<= |
Возвращает значение «Истина», если первое значение не больше второго. |
значение1 <= значение2 |
|
> |
Возвращает значение «Истина», если первое значение больше второго. |
значение1 > значение2 |
|
>= |
Возвращает значение «Истина», если первое значение не меньше второго. |
значение1 >= значение2 |
|
= |
Возвращает значение «Истина», если первое значение равно второму. |
значение1 = значение2 |
|
<> |
Возвращает значение «Истина», если первое значение не равно второму. |
значение1 <> значение2 |
Примечание: Если первое или второе значение в любом из случаев равно Null, результатом также является Null. Так как Null представляет собой неизвестное значение, результат сравнения со значением Null также неизвестен.
К началу страницы
|
Используйте логические операторы для объединения двух логических значений и возврата результата «Истина», «Ложь» или Null. Логические операторы также называются булевыми.
|
К началу страницы
|
Операторы объединения позволяют объединить два текстовых значения в одно.
|
К началу страницы
|
Специальные операторы возвращают результат «Истина» или «Ложь», как описано в таблице ниже.
|
Часто, для того чтобы продемонстрировать ограниченные возможности однослойных персептронов при решении задач прибегают к рассмотрению так называемой проблемы XOR – исключающего ИЛИ.
Суть задачи заключаются в следующем. Дана логическая функция XOR – исключающее ИЛИ. Это функция от двух аргументов, каждый из которых может быть нулем или единицей.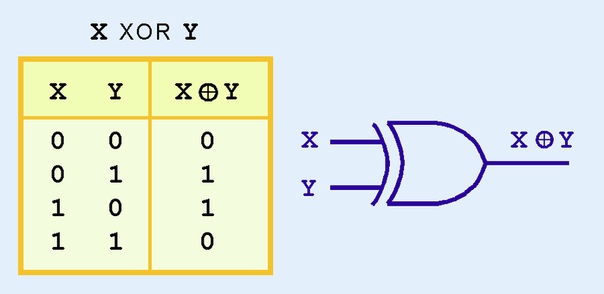
Она принимает значение , когда один из аргументов равен единице, но не оба, иначе . Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рисунке ниже.
Обозначим один вход через , а другой через , тогда все их возможные комбинации будут состоять из четырех точек на плоскости. Таблица ниже показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены и , единичный выход – и .
Один нейрон с двумя входами может сформировать решающую поверхность в виде произвольной прямой. Для того, чтобы сеть реализовала функцию XOR, заданную таблицей выше, нужно расположить прямую так, чтобы точки были с одной стороны прямой, а точки – с другой. Попытавшись нарисовать такую прямую на рисунке ниже, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, однослойная нейронная сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции XOR.
Однако функция XOR легко формируется уже двухслойной сетью, причем многими способами. Рассмотрим один из таких способов. Модернизуем сеть на рисунке, добавив еще один скрытый слой нейронов:
Отметим, что данная сеть дана как есть, т.е. можно считать, что она уже обучена. Цифры над стрелками показывают значения синаптических весов. В качестве функции активации применим функцию единичного скачка с порогом , имеющую следующий график:
Тогда результат работы такой нейронной сети можно представить в виде следующей таблицы:
Каждый из двух нейрон первого слоя формирует решающую поверхность в виде произвольной прямой (делит плоскость на две полуплоскости), а нейрон выходного слоя объединяет эти два решения, образуя решающую поверхность в виде полосы, образованной параллельными прямыми нейронов первого слоя :
Нейронная сеть, используемая в этой статье для решения задачи XOR, примитивна и не использует всех возможностей многослойных сетей. Очевидно, что многослойные нейронные сети обладают большей представляющей мощностью, чем однослойные, только в случае присутствия нелинейности. А в данной сети применена пороговая линейная функция активации. Такую сеть нельзя будет обучить, например, применив алгоритм обратного распространения ошибки.
| Название | Кнопка | Графический символ | Описание |
|---|---|---|---|
| Функция | Блок представляет собой функцию — действие или набор действий, выполняемых над исходным объектом (документом, ТМЦ и прочим) с целью получения заданного результата. Внутри блока помещается наименование функции. Временная последовательность выполнения функций задается расположением функций на диаграмме процесса сверху вниз. | ||
| Событие | | Событие — состояние, которое является существенным для целей управления бизнесом и оказывает влияние или контролирует дальнейшее развитие одного или более бизнес-процессов. Элемент отображает события, активизирующие функции или порождаемые функциями. Внутри блока помещается наименование события. | |
| Стрелка | Стрелка отображает связи элементов диаграммы процесса EPC между собой. Связь может быть направленной и ненаправленной в зависимости от соединяемых элементов и типа связи. | ||
| Оператор AND («И») | Оператор «И» используется для обозначения слияния/ветвления как функций, так и событий. Если завершение выполнения функции должно инициировать одновременно несколько событий, то это обозначается с помощью оператора «И», следующего после функции и перед событиями. На рисунке (Рис.1) завершение выполнения Функции одновременно инициирует события: Событие 1 и Событие 2. Рисунок 1 Если событие происходит только после обязательного завершения выполнения нескольких функций, то это обозначается с помощью оператора «И», следующего после функций и перед одиночным событием. На рисунке (Рис.2) Событие произойдет только после обязательного завершения Функции 1 и Функции 2. Рисунок 2 Если функция может начать выполняться только после того, как произойдут несколько событий, то это обозначается с помощью оператора «И», следующего после событий и перед функцией. На рисунке (Рис.3) Функция начнет выполняться только после того, как произойдут Событие 1 и Событие 2. Рисунок 3 Если одно событие может инициировать одновременное выполнение нескольких функций, то это обозначается с помощью оператора «И», следующего после события и перед функциями. На рисунке (Рис.4) Событие одновременно инициирует выполнение Функции 1 и Функции 2. Рисунок 4 | ||
| Оператор OR («ИЛИ») | Оператор «ИЛИ» используется для обозначения слияния/ветвления функций и для слияния событий. По правилам нотации EPC после одиночного события не может следовать разветвляющий оператор «ИЛИ». Если завершение выполнения функции может инициировать одно или несколько событий, то это обозначается с помощью оператора «ИЛИ», следующего после функции и перед событиями. На рисунке (Рис.5) завершение выполнения Функции 1 может инициировать 3 вида ситуаций: только Событие 1, только Событие 2, одновременно и Событие 1, и Событие 2. Рисунок 5 Если событие происходит после завершения выполнения одной или нескольких функций, то это обозначается с помощью оператора «ИЛИ», следующего после функций и перед одиночным событием. На рисунке (Рис.6) Событие может произойти либо после завершения выполнения Функции 1, либо после завершения выполнения Функции 2, либо после завершения выполнения и Функции 1, и Функции 2. Рисунок 6 Если функция может начать выполняться после того, как произойдет одно или несколько событий, то это обозначается с помощью оператора «ИЛИ», следующего после событий и перед функцией. На рисунке (Рис.7) Функция может начать выполняться либо после того, как произойдет Событие 1, либо после того, как произойдет Событие 2, либо после того, как произойдут оба события: Событие 1, и Событие 2. Рисунок 7 | ||
| Оператор XOR («Исключающее ИЛИ») | Оператор «Исключающее ИЛИ» используется для обозначения слияния/ветвления функций и для слияния событий. По правилам нотации EPC после одиночного события не может следовать разветвляющий оператор «Исключающее ИЛИ». Если завершение выполнения функции может инициировать только одно из событий в зависимости от условия, то это обозначается с помощью оператора «Исключающее ИЛИ», следующего за функцией и перед событиями. На рисунке (Рис.8) Функция инициирует либо только Событие 1, либо только Событие 2. Рисунок 8 Если событие происходит сразу после завершения выполнения либо одной функции, либо другой, то это обозначается с помощью оператора «Исключающее ИЛИ», следующего после функций и перед одиночным событием. На рисунке (Рис.9) Событие может произойти либо сразу после завершения выполнения Функции 1, либо сразу после завершения выполнения Функции 2. Рисунок 9 Если функция может начать выполняться сразу после того, как произойдет либо одно событие, либо другое, то это обозначается с помощью оператора «Исключающее ИЛИ», следующего после нескольких событий и перед функцией. На рисунке (Рис.10) Функция может начать выполняться сразу после того, как произойдет либо Событие 1, либо Событие 2. Рисунок 10 | ||
| Интерфейс процесса | Элемент, обозначающий внешний (по отношению к текущей диаграмме) процесс или функцию. Используется для указания взаимосвязи процессов: — обозначает предыдущий или следующий процесс по отношению к диаграмме рассматриваемого процесса; — обозначает процесс, откуда поступил или куда передается объект. Внутри блока помещается наименование внешнего процесса. На рисунке (Рис.11) показано, что договор является результатом выполнения процесса «Заключение договора». Рисунок 11 На рисунке (Рис.12) показано, что после окончания Процесса 1 (и наступления Событие 1) начинает выполняться Процесс 2. Рисунок 12. Диаграмма Процесса 1 На диаграмме Процесса 2 (Рис.13) показано, что перед началом Процесса 2 был завершен Процесс 1, инициировавший Событие 1. Рисунок 13. Диаграмма Процесса 2 | ||
| Субъект | Используется для отображения на диаграмме организационных единиц (должности, подразделения, роли, внешнего субъекта) — исполнителей, владельцев или участников функций. Внутри блока помещается наименование организационной единицы. | ||
| Бумажный документ | Используется для отображения на диаграмме бумажных документов, сопровождающих выполнение функции. Внутри блока помещается наименование бумажного документа. | ||
| Электронный документ | Используется для отображения на диаграмме электронных документов, сопровождающих выполнение функции. Внутри блока помещается наименование электронного документа. | ||
| ТМЦ | Используется для отображения на диаграмме товарно-материальных ценностей (ТМЦ), сопровождающих выполнение функции. Внутри блока помещается наименование ТМЦ. | ||
| Информация | Используется для отображения на диаграмме информационных потоков, сопровождающих выполнение функции. Внутри блока помещается наименование информационного потока. | ||
| Информационная система | Используется для отображения на диаграмме информационной системы, поддерживающей выполнение функции. Внутри блока помещается наименование информационной системы. | ||
| Модуль информационной системы | Используется для отображения на диаграмме модуля информационной системы, поддерживающего выполнение функции. Внутри блока помещается наименование модуля информационной системы. | ||
| Функция информационной системы | Используется для отображения на диаграмме функции информационной системы, поддерживающей выполнение функции. Внутри блока помещается наименование функции информационной системы. | ||
| База данных | Используется для отображения на диаграмме базы данных, сопровождающей выполнение функции. Внутри блока помещается наименование базы данных. | ||
| Термин | Используется для отображения на диаграмме объектов, сопровождающих выполнение функции. Наименования этих объектов — термины, используемые в организации. Внутри блока помещается наименование термина. Элемент может быть использован для обозначения данных, передаваемых между процессами или обрабатываемых при выполнении процессов. Элемент может быть также использован для обозначения статусов бумажных/электронных документов и других элементов справочника «Объекты деятельности». На рисунке (Рис.14) статус документа «Акт выполненных работ» устанавливается с помощью термина «Подписанный». Рисунок 14 | ||
| Набор объектов | Используется для отображения на диаграмме наборов объектов, сопровождающих выполнение функции, например, «Документация по проекту». Внутри блока помещается наименование набора объектов. | ||
| Прочее | Используется для отображения на диаграмме потоков объектов, которые нельзя отнести ни к одной из предопределенных групп справочника «Объекты деятельности». Внутри блока помещается наименование прочего объекта. |
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними.» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
Операция исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Wikimedia Foundation. 2010.
Мы узнаем о Ex OR Gate в этом руководстве. Ворота Ex OR — это ворота Exclusive OR. Это не часто используется как включающий вентиль ИЛИ, который является не чем иным, как обычным вентилем ИЛИ. Гейт XOR имеет собственное значение. Мы изучим символ, таблицу истинности шлюза XOR, реализацию с использованием других вентилей (AND, OR, NAND, NOR), популярные ИС XOR и некоторые важные приложения Exclusive OR Gate (XOR Gate).
Шлюз исключающего ИЛИ, также известный как вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ или вентиль исключающего ИЛИ, является важным цифровым логическим вентилем, который реализует логику исключающего ИЛИ.е., выход ВЫСОКИЙ, если и только если один из входов ВЫСОКИЙ. Если оба входа — НИЗКИЙ или ВЫСОКИЙ, то выход — НИЗКИЙ.
Существует несколько стандартов для определения электронного компонента. Как правило, мы следуем стандартам IEEE (Институт инженеров по электротехнике и электронике) и IEC (Международной электротехнической комиссии). Символ логики XOR в стандартах IEEE и IEC показан ниже.
Логическое выражение для логического элемента XOR не может быть определено напрямую, как логические элементы AND, OR.Поскольку это гибридный вентиль, логическое выражение выхода элемента XOR дается путем объединения умножения, сложения и инвертирования входов. Мы должны использовать карты Карно или K-карты вместе с таблицей истинности, чтобы получить логическое выражение логического элемента XOR.
Таблица истинности логического элемента XOR показана в таблице ниже. Из этого ясно, что вентиль XOR создает логический LOW, то есть логический «0» на своем выходе, когда оба входа одинаковы (оба могут быть LOW или оба могут быть HIGH).
Низкая логика, которая является логическим «0», на его выходе, когда когда два входа различны, он создает высокое логическое значение, то есть логическую «1» на своем выходе.
| Входы | Выход | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Представление K-карты приведенной выше таблицы истинности шлюза XOR показано ниже. .
Используя приведенную выше таблицу истинности и соответствующую K-карту, мы можем теперь вывести логическое выражение для шлюза XOR. Если A и B являются входами логического элемента XOR, его выход представлен как:
AB + AB
Выход XOR представлен как:
A ⊕ B
Его также можно записать как:
(A + B) (A + B)
Применяя закон Де Моргана, вышеупомянутое логическое выражение также можно записать как:
(A + B) (AB)
Элемент EX-OR определяется как гибридный логический вентиль с 2 входами для выполнения операции исключительного разъединения.Из приведенных выше вычислений основное логическое выражение логического элемента XOR:
A B + A B
Итак, схема XOR с 2 входами разработана с использованием логических элементов AND, OR и NOT, как показано ниже.
Выход логического элемента XOR с двумя входами ВЫСОКИЙ только тогда, когда один из его входов ВЫСОКИЙ. Если оба входа одинаковы, то выход НИЗКИЙ.
Если конкретный вентиль недоступен напрямую, мы можем спроектировать вентиль XOR, используя несколько вентилей.Логический элемент EX-OR может быть спроектирован с использованием основных логических вентилей, таких как вентиль И-НЕ и вентиль ИЛИ-НЕ, поскольку они являются универсальными вентилями.
Давайте теперь посмотрим, как мы можем реализовать ворота XOR, используя ворота NOR. Для этого мы должны переписать приведенное выше логическое уравнение XOR.
Q = AB + AB
Q = AB + AB + AA + BB
Q = (A + B) (A + B)
Q = (A + B) (A + B) = (A ‘ + B ‘) (A + B)
Взяв дополнение с обеих сторон, получаем:
Q = ((A’ + B ‘) (A + B))
Используя закон де Моргана, получаем:
Q = (A ‘+ B’) + (A + B) = (A ‘+ B’) ‘+ (A + B)’
Еще раз взяв дополнение с обеих сторон, получаем:
Q = (( A ‘+ B’) ‘+ (A + B)’) = ((A ‘+ B’) ‘+ (A + B)’) ‘
Это уравнение выглядит так, как будто оно может быть реализовано с помощью NOR Gates.Всего нам нужно пять вентилей NOR (два для инвертирования A и B, один для NOR A и B, один для NOR A ’и B’ и последний для получения приведенного выше уравнения). На следующем изображении показан вентиль XOR, реализованный с использованием шлюзов NOR.
Давайте теперь посмотрим, как мы можем реализовать ворота XOR с помощью шлюзов NAND. Для этого мы должны переписать приведенное выше логическое уравнение XOR.
Q = AB + AB
Q = AB + AB + AA + BB
Q = (A + B) (A + B)
Q = (A + B) (A + B) = (A + B) (A ‘+ B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) (AB)
Теперь нам нужно реализовать эту схему с использованием NAND. ворота.
Q = A (AB) + B (AB) = A (AB) ‘+ B (AB)’
Взяв дополнение с обеих сторон, получаем:
Q = (A (AB) + B (AB) ) ‘= (A (AB)’ + B (AB) ‘)
Q = (A (AB))’ (B (AB)) ‘= (A (AB)’) (B (AB) ‘)
Наконец, еще раз нанесите дополнение с обеих сторон.
Q = (A (AB) ‘)’ (B (AB) ‘)’ = ((A (AB) ‘)’ (B (AB) ‘)’) ‘
Это уравнение выглядит так, как будто его можно реализовать с использованием NAND Gates. Нам полностью нужны наши ворота NAND. На следующем изображении показан вентиль XOR, реализованный с использованием шлюзов NAND.
Давайте теперь посмотрим, как мы можем реализовать вентиль XOR, используя вентили И, И и ИЛИ. Для этого мы должны переписать приведенное выше логическое уравнение XOR.
Q = AB + AB
Q = AB + AB + AA + BB
Q = (A + B) (A + B)
Q = (A + B) (A + B) = (A + B) (A ‘+ B’)
Применяя закон де Моргана ко второму члену в приведенном выше уравнении, мы получаем:
Q = (A + B) (AB)
Первый член в приведенном выше уравнении требует Логический элемент ИЛИ, второй член требует логического элемента И-НЕ, и окончательное уравнение может быть получено с использованием логического элемента И.
Импульсный режим 2 входного логического элемента XOR показан ниже.
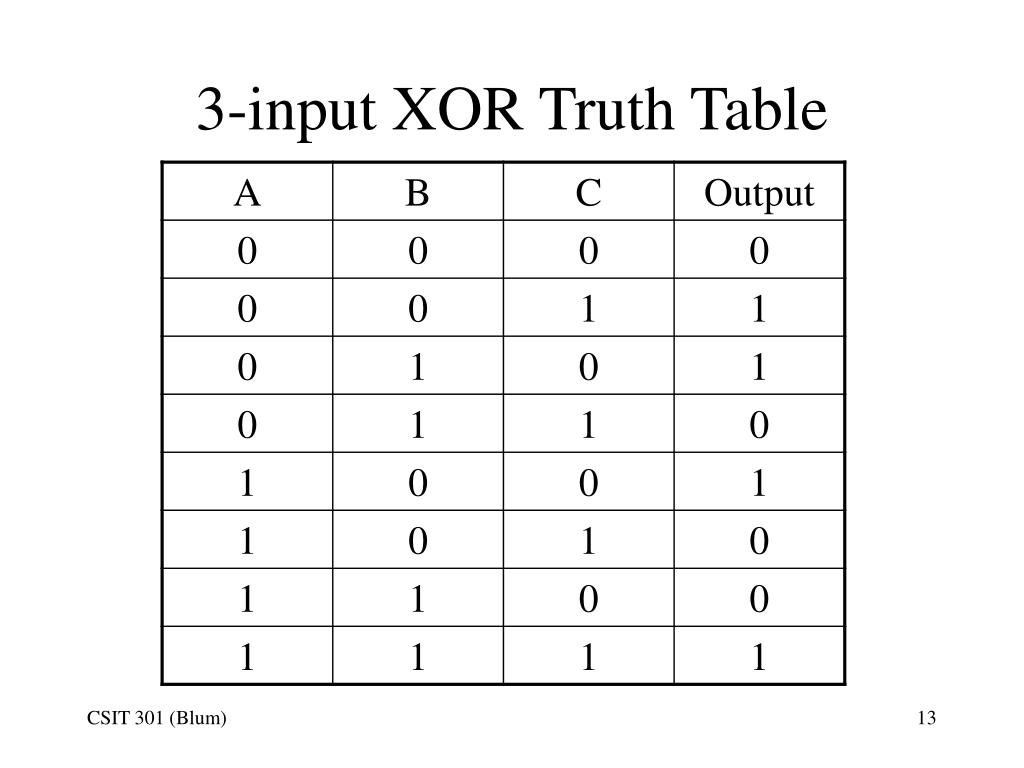
В некоторых случаях нам нужны шлюзы XOR с более чем 2 входами. Функция XOR для более чем двух входов называется «Нечетная функция» или «Сумма по модулю 2». Логическая функция для элемента XOR с 3 входами:
Q = A ⊕ B ⊕ C = A B C + A B C + A B C + A B C
Таблица истинности и логический символ для элемента XOR с 3 входами приведены ниже.
Для 3-входных вентилей XOR мы можем иметь HIGH вход, когда нечетные числа входов находятся на HIGH уровне. Таким образом, вентиль ИЛИ с 3 входами называется «логическим элементом ИЛИ с нечетной функцией».
| Входы | Выход | ||
| A | B | C | Q |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Ниже приводится список некоторых из них. общедоступные ИС XOR.
| Номер микросхемы | Описание |
| 4030 | Четырехходовые ворота XOR с двумя входами |
| 4070 | Четырехходовые ворота XOR с двумя входами |
| 7486 | Quad 2- Входные ворота XOR |
| 74LS86 | Четыре входа XOR с двумя входами |
| 741G86 | Одиночные ворота с двумя входами Ex-OR |
| 74136 | Четыре входа XOR с двумя входами и выходами с открытым коллектором |
| 74386 | Quad 2-Input XOR Gates |
Из них самой популярной ИС EX-OR на основе логики TTL является 74LS86, которая представляет собой Quad 2-input XOR IC.Что касается микросхемы XOR Gate IC на основе логики CMOS, то популярным выбором является четырехвходовая микросхема CD4030 с двумя входами XOR.
IC 7486 представляет собой элемент с четырьмя входами XOR с 2 входами, т.е.содержит четыре логических элемента XOR с 2 входами в одном корпусе. Схема выводов и описание выводов ИС показаны ниже.
| Номер контакта | Описание |
| 1 | Строб 1 Вход A |
| 2 | Строб 1 Вход B |
| 3 | Строб 1 Выход Y |
| 4 | Строб 2 Вход A |
| 5 | Строб 2 Вход B |
| 6 | Строб 2 Выход Y |
| 7 | Земля |
| 8 | Выход 3 Выход Y |
| 9 | Строб 3, вход A |
| 10 | Строб 3, вход B |
| 11 | Строб 4, выход Y |
| 12 | Строб 4, вход A |
| 13 | Затвор 4 Вход B |
| 14 | Положительное питание |
Логический вентиль XOR используется во многих приложениях.Некоторые из них описаны ниже.
Мы можем разработать однобитовый сумматор (также известный как полусумматор), который будет складывать два бита и производить однобитовый вывод. Ниже показан однобитовый сумматор, созданный с использованием логического элемента XOR.
Например, если мы сложим два бита «1» и «1» в двоичном сложении, мы получим ответ «10», а в методе десятичного сложения мы получим 2. Основной принцип полусумматоров заключается в том, что конечная сумма достигается выходом логического элемента XOR, а бит переноса вычисляется логическим элементом AND.
Мы можем каскадировать множество схем одноразрядного сумматора, чтобы сформировать схему n-разрядного сумматора, чтобы вычислить сумму более длинных двоичных чисел.
Линейные регистры сдвига также называются генераторами псевдослучайных чисел (PNR). Чтобы сгенерировать случайные числа, мы располагаем логический вентиль XOR в определенном порядке, формируя регистр сдвига с линейной обратной связью.
Логический элемент XOR может создавать входной сигнал низкого уровня i.е., 0, когда все его входы ВЫСОКИЙ или НИЗКИЙ. Когда мы ищем конкретную последовательность битов в длинной последовательности данных, мы используем вентили XOR, чтобы найти требуемую последовательность битов данных.
Точность нахождения требуемой строки битов данных в целевой последовательности определяется путем вычисления количества полученных нулей. Во многих устройствах связи, таких как декодеры и приемники CDMA, мы используем сопутствующие устройства, которые используются для извлечения четности определенной последовательности псевдослучайных чисел в группе последовательности PRN.
Полное руководство по эксклюзивному OR Gate (XOR Gate). Вы изучили символ, таблицу истинности и логическое выражение шлюза XOR, реализацию шлюза XOR с использованием вентилей NOR и NAND, трехвходовой вентиль XOR, его символ, таблицу истинности и логическое выражение, некоторые общие и популярные ИС XOR, а также некоторые важные приложения XOR Gate.
Учебное пособие по таблице истинности логической алгебрыВсе мы любим компьютеры.Они могут делать так много удивительных вещей. За пару десятилетий компьютеры полностью изменили почти все аспекты жизни человека.
Они могут выполнять задачи разной степени сложности, просто переворачивая нули и единицы. Замечательно видеть, как такое простое действие может привести к такой сложности.
Но я уверен, что вы все знаете, что такая сложность не может быть достигнута (практически) простым случайным переворачиванием чисел. За этим действительно есть какие-то доводы.Существуют правила, регулирующие то, как это должно быть сделано. В этой статье мы обсудим эти правила и увидим, как они управляют «мышлением» компьютеров.
Правила, о которых я говорил выше, описываются в области математики, называемой булевой алгеброй.
В своей книге 1854 года британский математик Джордж Буль предложил систематический набор правил для манипулирования ценностями истины. Эти правила дали математическую основу для работы с логическими предложениями.Эти наборы основ привели к развитию булевой алгебры.
Чтобы лучше понять булеву алгебру, мы сначала должны понять сходства и различия между булевой алгеброй и другими формами алгебры.
Алгебра, в общем, занимается изучением математических символов и операций, которые могут быть выполнены с этими символами.
Эти символы не имеют самостоятельного значения. Они представляют собой какое-то другое количество. Именно эта величина придает значение этим символам, и именно с этой величиной фактически выполняются операции.
Логическая алгебра также имеет дело с символами и правилами, которые управляют операциями с этими символами, но разница заключается в , что эти символы представляют .
В случае обычной алгебры символы представляют действительные числа, тогда как в булевой алгебре они представляют значения истины.
На изображении ниже показан весь набор вещественных чисел. Набор действительных чисел включает натуральные числа (1, 2, 3, 4 ….), целые числа (все натуральные числа и 0), целые числа (…..- 2, -1, 0, 1, 2, 3 …) и так далее. Обычная алгебра имеет дело со всем этим набором чисел.
Значения «Истина» для сравнения состоят из набора только двух значений: «Ложь» и «Истина». Здесь я хотел бы указать на тот факт, что мы можем использовать любой другой символ для представления этих значений.
Например, в информатике мы чаще всего представляем эти значения, используя 0 и 1. 0 используется для False и 1 для True.
Вы также можете сделать это более изящными способами, представив значения истинности некоторыми другими символами, такими как Кошки и Собаки или Бананы и Апельсины.
Дело в том, что внутреннее значение этих символов останется неизменным независимо от того, какой символ вы используете. Но убедитесь, что вы не меняете символы при выполнении операций.
Теперь вопрос в том, что если (Истина и Ложь), (0 и 1) — это просто представления, то что они пытаются представить?
Значение, лежащее в основе значений истинности, исходит из области логики, где значения истинности используются, чтобы определить, является ли предложение «Истинным» или «Ложным».Здесь значения истинности представляют отношение предложения к истине, то есть, является ли предложение истинным или ложным.
Предложение — это просто утверждение вроде «Все кошки милые».
Если вышеприведенное утверждение верно, то мы присваиваем ему значение истинности «Истина» или «1», в противном случае мы присваиваем ему «Ложь» или «0».
В цифровой электронике истинные значения используются для представления состояний «включено» и «выключено» электронных схем. Мы обсудим это подробнее позже в этой статье.
Как и в обычной алгебре, в булевой алгебре есть операции, которые можно применять к значениям для получения некоторых результатов. Хотя эти операции не похожи на операции в обычной алгебре, потому что, как мы обсуждали ранее, булева алгебра работает со значениями истины, а не с действительными числами.
OR : Также известен как Disjunction . Эта операция выполняется с двумя логическими переменными.Результатом операции ИЛИ будет 0, когда оба операнда равны 0, в противном случае — 1.
Чтобы получить более четкое представление о том, что делает эта операция, мы можем визуализировать ее с помощью приведенной ниже таблицы истинности .
Степень
07.07# And #31.12.07# Таблицы истинности дают нам подробное представление о том, что делают логические операции, а также они служат удобным инструментом для выполнения логических операций.
ИЛИ Операция
Переменная-1 Переменная-2 Выход
0 0 0
0 1 1
1 0 1
1 1 1 И : Также известна как Соединение .Эта операция выполняется с двумя логическими переменными. Результатом операции И будет 1, когда оба операнда равны 1, в противном случае — 0. Таблица истинности представлена следующим образом.
И Работа
Переменная-1 Переменная-2 Выход
0 0 0
0 1 0
1 0 0
1 1 1 НЕ : Также известно как Отрицание . Эта операция выполняется только с одной переменной. Если значение переменной равно 1, то эта операция просто преобразует его в 0, а если значение переменной равно 0, то оно преобразует его в 1.
Не работает
Выход переменной-1
0 1
1 0 После своего первоначального развития булева алгебра в течение очень долгого времени оставалась одним из тех понятий в математике, которые не имели каких-либо значительных практических приложений.
В 1930-х годах американский математик Клод Шеннон понял, что булеву алгебру можно использовать в схемах, где двоичные переменные могут представлять сигналы «низкого» и «высокого» напряжения или состояния «включено» и «выключено».
Эта простая идея создания схем с помощью булевой алгебры привела к развитию цифровой электроники, которая внесла большой вклад в разработку схем для компьютеров.
Цифровые схемы реализуют логическую алгебру с помощью логических вентилей. Логические ворота — это схемы, которые представляют собой логическую операцию. Например, вентиль ИЛИ будет представлять операцию ИЛИ. То же самое касается ворот НЕ и И.
Наряду с основными логическими вентилями у нас также есть логические вентили, которые могут быть созданы с использованием комбинации базовых логических вентилей.
И-НЕ : вентиль И-НЕ образован комбинацией вентилей НЕ и И. Логический элемент И-НЕ дает на выходе 0, если оба входа равны 1, в противном случае — 1.
Элемент И-НЕ содержит свойство функциональной полноты, что означает, что любая логическая функция может быть реализована только с использованием комбинации элементов И-НЕ.
NAND Gate
Переменная-1 Переменная-2 Выход
0 0 1
0 1 1
1 0 1
1 1 0 NOR : ворота NOR образованы комбинацией элементов NOT и OR.Логический элемент ИЛИ-НЕ дает на выходе 1, если оба входа равны 0, в противном случае — 0.
Элемент ИЛИ-НЕ, как и элемент И-НЕ, обладает свойством функциональной полноты, что означает, что любая логическая функция может быть реализована просто с помощью комбинации элементов ИЛИ-НЕ. Только.
NOR Ворота
Переменная-1 Переменная-2 Выход
0 0 1
0 1 0
1 0 0
1 1 0 Большинство цифровых схем построено с использованием логических элементов И-НЕ или ИЛИ-ИЛИ из-за их функциональной полноты, а также из-за того, что их легко изготовить.
Помимо вышеупомянутых ворот, у нас также есть некоторые особые ворота, которые служат определенной цели. Это следующие элементы:
XOR : вентиль XOR или вентиль Исключающее ИЛИ — это особый тип логического элемента, который дает 0 на выходе, если оба входа равны 0 или 1, в противном случае он дает 1.
XOR Ворота
Переменная-1 Переменная-2 Выход
0 0 0
0 1 1
1 0 1
1 1 0 XNOR : вентиль XNOR или вентиль Exclusive-NOR — это особый тип логического элемента, который дает 1 на выходе, когда оба входа равны 0 или 1, в противном случае он дает 0.
Ворота XNOR
Переменная-1 Переменная-2 Выход
0 0 1
0 1 0
1 0 0
1 1 1 Итак, со всем этим мы можем закончить здесь обсуждение булевой алгебры. Я надеюсь, что теперь у вас есть достойное представление о том, что такое булева алгебра.
Это определенно не все, что вам нужно знать о булевой алгебре. Булева алгебра содержит множество концепций и деталей, которые мы не смогли обсудить в этой статье.
До сих пор вы счастливо жили в мире всего с тремя основными логическими воротами. Пора разрушить это восприятие! Приготовьтесь к открытию … эксклюзивной модели OR .
Исключающее ИЛИ, сокращенное до XOR, похоже на логический элемент ИЛИ с одним важным отличием. Можете ли вы сказать по таблице истинности ?:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Когда мы говорим эксклюзивный , мы имеем в виду именно это.XOR производит только 1, когда одиночный вход также равен 1. Если два или более входов равны 1, вентиль XOR выдает 0.
Оказывается, вентиль XOR — невероятно полезная функция в цифровой логике. Фактически настолько полезен, что он получает свой собственный символ схемы — своего рода модифицированный вентиль ИЛИ с вогнутой линией, предшествующей вентилю, к которому мы привыкли:
Как и все предыдущие эксперименты, вентиль XOR может быть реализован с помощью трех основных цифровых логических вентилей. Сочетание НЕ, И и ИЛИ:
Давайте LogicBlock it!
Создайте XOR, как показано ниже:
Выход схемы логических блоков XOR представлен желтым светодиодом на последнем логическом элементе ИЛИ .
Подтвердите истинность таблицы истинности XOR, переключив оба входа. Светодиод на блоке ИЛИ должен загореться только тогда, когда у вас включен один или другой из входов .
Помните NAND и NOR? Что ж, у XOR есть собственное дополнение… XNOR . Как и два других отрицательных логических элемента, XNOR имеет собственную схему с пузырьками:
Таблица истинности для 2-входного XNOR выглядит следующим образом:
| Вход A | Вход B | Выход |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 |
Что действительно здорово в XNOR, так это то, что он оказывается верным только тогда, когда , оба входа совпадают, .Поэтому мы называем этот оператор логическим равенством . Вы даже можете использовать знак равенства (=) в качестве оператора XNOR. Оператор равенства используется повсюду в электронике и программировании. Если вам когда-нибудь понадобится проверить, равны ли два оператора, будет задействован XNOR.
Эй, у нас завалялся еще один НЕ Блок, давайте сделаем схему XNOR LogicBlocks! Замените силовой блок на НЕ блок и подключите силовой блок к его концу.
Выход этой схемы представлен красным светодиодом на последнем блоке НЕ .
| XOR | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | В | К | Д | E | Факс |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | B | А | D | С | F | E |
| 2 | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 | А | B | 8 | 9 | E | F | С | D |
| 3 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 | B | А | 9 | 8 | F | E | D | С |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | С | D | E | F | 8 | 9 | А | B |
| 5 | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 | D | С | F | E | 9 | 8 | B | А |
| 6 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 | E | F | С | D | А | B | 8 | 9 |
| 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | С | B | А | 9 | 8 |
| 8 | 8 | 9 | А | B | С | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 9 | 8 | B | А | D | С | F | E | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 |
| А | А | B | 8 | 9 | E | F | С | D | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 |
| B | B | А | 9 | 8 | F | E | D | С | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 |
| К | С | D | E | F | 8 | 9 | А | B | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| Д | D | С | F | E | 9 | 8 | B | А | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 |
| E | E | F | С | D | А | B | 8 | 9 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 |
| Ф. | F | E | D | С | B | А | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Идентификационные данные: х ⊕ 0 = х (т.е., 0 ⊕ 0 = 0, 1 ⊕ 0 = 1) | ||||||||||||||||
И ТАБЛИЦА (ШЕСТИГР.)
| И | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | В | К | Д | E | Факс |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 2 | 2 | 0 | 0 | 2 | 2 | 0 | 0 | 2 | 2 | 0 | 0 | 2 | 2 |
| 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
| 4 | 0 | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 0 | 0 | 0 | 0 | 4 | 4 | 4 | 4 |
| 5 | 0 | 1 | 0 | 1 | 4 | 5 | 4 | 5 | 0 | 1 | 0 | 1 | 4 | 5 | 4 | 5 |
| 6 | 0 | 0 | 2 | 2 | 4 | 4 | 6 | 6 | 0 | 0 | 2 | 2 | 4 | 4 | 6 | 6 |
| 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 9 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 8 | 9 | 8 | 9 | 8 | 9 | 8 | 9 |
| А | 0 | 0 | 2 | 2 | 0 | 0 | 2 | 2 | 8 | 8 | А | А | 8 | 8 | А | А |
| B | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 8 | 9 | А | B | 8 | 9 | А | B |
| К | 0 | 0 | 0 | 0 | 4 | 4 | 4 | 4 | 8 | 8 | 8 | 8 | С | С | С | С |
| Д | 0 | 1 | 0 | 1 | 4 | 5 | 4 | 5 | 8 | 9 | 8 | 9 | С | D | С | D |
| E | 0 | 0 | 2 | 2 | 4 | 4 | 6 | 6 | 8 | 8 | А | А | С | С | E | E |
| Ф. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F |
| Идентификационные данные: x • 0 = 0 (т. Е.е., 0 • 0 = 0, 1 • 0 = 0) | ||||||||||||||||
ИЛИ ТАБЛИЦА (HEX)
| ИЛИ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | В | К | Д | E | Факс |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F |
| 1 | 1 | 1 | 3 | 3 | 5 | 5 | 7 | 7 | 9 | 9 | B | B | D | D | F | F |
| 2 | 2 | 3 | 2 | 3 | 6 | 7 | 6 | 7 | А | B | А | B | E | F | E | F |
| 3 | 3 | 3 | 3 | 3 | 7 | 7 | 7 | 7 | B | B | B | B | F | F | F | F |
| 4 | 4 | 5 | 6 | 7 | 4 | 5 | 6 | 7 | С | D | E | F | С | D | E | F |
| 5 | 5 | 5 | 7 | 7 | 5 | 5 | 7 | 7 | D | D | F | F | D | D | F | F |
| 6 | 6 | 7 | 6 | 7 | 6 | 7 | 6 | 7 | E | F | E | F | E | F | E | F |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | F | F | F | F | F | F | F | F |
| 8 | 8 | 9 | А | B | С | D | E | F | 8 | 9 | А | B | С | D | E | F |
| 9 | 9 | 9 | B | B | D | D | F | F | 9 | 9 | B | B | D | D | F | F |
| А | А | B | А | B | E | F | E | F | А | B | А | B | E | F | E | F |
| B | B | B | B | B | F | F | F | F | B | B | B | B | F | F | F | F |
| К | С | D | E | F | С | D | E | F | С | D | E | F | С | D | E | F |
| Д | D | D | F | F | D | D | F | F | D | D | F | F | D | D | F | F |
| E | E | F | E | F | E | F | E | F | E | F | E | F | E | F | E | F |
| Ф. | F | F | F | F | F | F | F | F | F | F | F | F | F | F | F | F |
| Идентификационные данные: х + 0 = х (т.е., 0 + 0 = 0, 1 + 0 = 1) | ||||||||||||||||
ОБЩИЕ ИДЕНТИФИКАЦИИ
| XOR | И | ИЛИ | |
|---|---|---|---|
| Икс ? 0 | х ⊕ 0 = х | x • 0 = 0 | х + 0 = х |
| Икс ? 1 | x ⊕ 1 = ¬x | x • 1 = x | х + 1 = 1 |
| Икс ? х | х ⊕ х = 0 | х • х = х | х + х = х |
| Икс ? ¬x | х ⊕ ¬x = 1 | x • ¬x = 0 | x + ¬x = 1 |
Отправлено НК У Сарада Анушка | 1711086
Логический вентиль — это устройство, которое действует как строительный блок для цифровых схем. Они выполняют основные логические функции, которые являются фундаментальными для цифровых схем. В большинстве электронных устройств, которые мы используем сегодня, есть логические вентили. Например, логические вентили могут использоваться в таких технологиях, как смартфоны, планшеты или в устройствах памяти.
В схеме логические вентили будут принимать решения на основе комбинации цифровых сигналов, поступающих с их входов.Большинство логических вентилей имеют два входа и один выход. Логические вентили основаны на булевой алгебре. В любой момент каждый терминал находится в одном из двух двоичных состояний: ложно, или истинно, . Ложь представляет 0, а истина представляет 1. В зависимости от типа используемого логического элемента и комбинации входов двоичный выход будет отличаться. Логический вентиль можно представить себе как выключатель света, в котором в одном положении выход выключен — 0, а в другом — включен — 1. Логические вентили обычно используются в интегральных схемах (IC).
Базовые логические элементыСуществует семь основных логических вентилей: И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕ, И-НЕ, ИЛИ-ИЛИ и ИСКЛЮЧИТЕЛЬНОЕ ИЛИ.
И | ИЛИ | XOR | НЕ | NAND | NOR | XNOR
Логический элемент И назван так потому, что, если 0 называется «ложным», а 1 — «истинным», этот элемент действует так же, как логический оператор «И». На следующем рисунке и в таблице показаны символы схемы и логические комбинации для логического элемента И. (В символе входные клеммы слева, а выходные клеммы справа.) Выход «истина», когда оба входа «истина». В противном случае вывод будет «ложным». Другими словами, выход равен 1 только тогда, когда оба входа один И два равны 1.
И ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логический элемент ИЛИ получил свое название благодаря тому факту, что он ведет себя по образцу логического включающего «или».«Выход -« истина », если один или оба входа равны« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода будет 1, по крайней мере, вход один ИЛИ два должны быть 1.
OR ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
Шлюз XOR ( исключающее ИЛИ, ), логический элемент , действует так же, как логическое «или / или».«Выход -« истина », если один из входов, но не оба,« истина ». Выход« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
ворота XOR
| Вход 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический инвертор , иногда называемый вентилем НЕ , чтобы отличать его от других типов электронных инверторных устройств, имеет только один вход.Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Инвертор или НЕ вентильЛогический элемент И-НЕ работает как логический элемент И, за которым следует вентиль НЕ. Он действует как логическая операция «и» с последующим отрицанием. На выходе будет «ложь», если оба входа «истина». В противном случае на выходе будет «истина».
логический элемент NAND
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический элемент ИЛИ представляет собой комбинацию логического элемента ИЛИ, за которым следует инвертор.Его выход будет «истина», если оба входа «ложь». В противном случае вывод будет «ложным».
NOR ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Логический элемент XNOR (исключающее ИЛИ) — это комбинированный вентиль XOR, за которым следует инвертор.Его вывод — «истина», если входы одинаковые, и «ложь», если входы разные.
Вентиль XNOR
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Сложные операции могут выполняться с использованием комбинаций этих логических вентилей.Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Высокий или низкий двоичные состояния представлены разными уровнями напряжения.Логическое состояние терминала может и обычно часто изменяется по мере того, как схема обрабатывает данные. В большинстве логических вентилей низкое состояние составляет приблизительно ноль вольт (0 В), а высокое состояние — приблизительно пять вольт положительного напряжения (+5 В).
Логические вентили могут быть выполнены из резисторов и транзисторов или диодов. Резистор обычно можно использовать как подтягивающий или понижающий резистор. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логического элемента для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы подключены к земле (0 В).
Обычно используются логические вентили TTL и CMOS. ИС TTL или транзисторно-транзисторной логики будут использовать биполярные переходные транзисторы типа NPN и PNP. КМОП, или дополнительные металл-оксидно-кремниевые ИС, построены из полевых транзисторов типа MOSFET или JFET. ИС TTL обычно обозначают как микросхемы серии 7400, в то время как ИС КМОП часто обозначают как микросхемы серии 4000.
| Библиотека: | Base |
| Введено: | 2.0 Beta 1 для XOR / Odd / Even; 2.0 Beta 6 для XNOR |
| Внешний вид: |
Шлюзы XOR, XNOR, четности и нечетной четности для каждого вычисления соответствующая функция входов, и вывести результат на выход.Таблица истинности с двумя входами для ворот следующая.
| x | y | XOR | XNOR | Нечетный | Четный |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
Любые неуказанные входы (т. Е. Плавающие) игнорируются. Я упал входы с плавающей точкой, то выход тоже с плавающей точкой. Если какой-либо из входы — это значение ошибки (например,g., если в тот же провод), то на выходе также будет значение ошибки.
Многобитовые версии каждого логического элемента будут выполнять свои однобитовые побитовое преобразование на его входах.
Примечание: Многие авторитетные источники утверждают, что сформированный XOR поведение гейта должно соответствовать вентилю нечетной четности, но есть нет согласия по этому поводу. Поведение Logisim для вентилей XOR основано на по стандарту IEEE 91. Это также согласуется с интуитивно понятным значение, лежащее в основе термина эксклюзив или : официант спрашивает хотите ли вы гарнир из картофельного пюре, моркови, гороха или капусты slaw примет только один вариант, а не три, каковы бы ни были некоторые авторитеты могу вам сказать.(Я должен признать, однако, что я не подвергал это заявление к строгой проверке.)
Обратите внимание, что если вы используете профилированные ворота, западная сторона XOR и Ворота XNOR будут изогнутыми. Тем не менее, входные контакты выстроены в линию. Logisim нарисует короткие отрезки, иллюстрирующие это; и если вы промахнетесь заглушка, он будет молча предположить, что вы не хотели его промахнуть.В «вид принтера», эти заглушки не будут отображаться, если они не подключены к проводам.
Нет.
Нет.