8-900-374-94-44
Разность потенциалов между двумя точками в схеме представляет собой разность их напряжений (относительно общей точки, обычно земли). Например, разность потенциалов между точками А и В на рис. 1.8 VAВ = (VA — VВ), где VA — напряжение в точке А и VВ — напряжение в точке В. Напряжения Уд и Уд измеряются относительно провода Е, имеющего нулевой потенциал. Напряжение в любой точке электрической схемы измеряется относительно нулевого провода, корпуса или земли.
Например, если VA = 5 В и VВ = 3 В, то VAВ = VA — VВ = 5 — 3 = 2 В (рис. 1.9(а)).
Напряжения могут отличаться по знаку — быть отрицательными и положительными. Разность потенциалов между двумя точками, имеющими напряжения с противоположными знаками, равна сумме этих напряжений.
Например, если VС = 3 В, а VD = -2 В, то V = VС + VD = 3 + 2 = 5 В (рис. 1.9(б)).
Итак, если два напряжения имеют одинаковую полярность, или одинаковые знаки, то разность потенциалов между ними равна их разности. Если же напряжения имеют разные знаки, то разность потенциалов между ними равна их сумме.
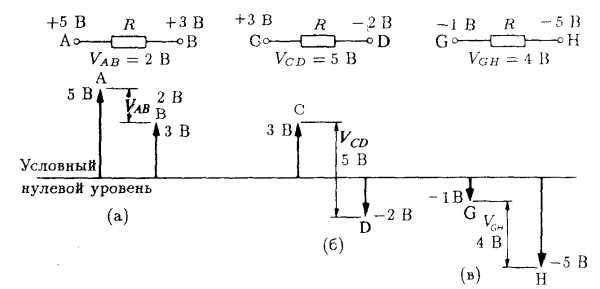
Рис. 1.9. Наглядное представление напряжений с разными знаками относительно линии нулевого потенциала
Параллельное соединение резисторов
На рис. 1.10 изображены два резистора, R1 и R2 соединенные параллельно. Ток I от батареи разветвляется в точке А на ток I1, протекающий через сопротивление R1, и ток I2, протекающий через сопротивление R2. В точке В эти токи складываются и образуют полный ток I = I1 + I2.
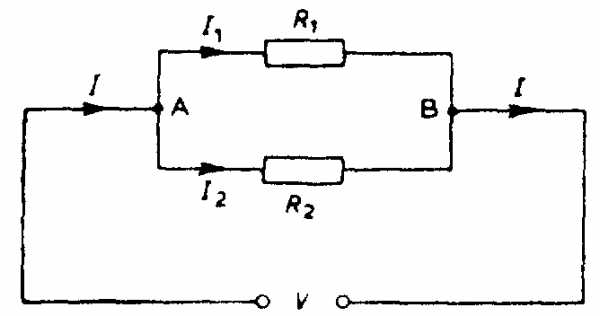
Рис. 1.10. Два резистора, соединенные параллельно
С другой стороны, к каждому резистору приложено полное напряжение V, т. е.
Полное напряжение V = напряжению на R1
= напряжению на R2.
Общее сопротивление
Общее сопротивление (R) двух резисторов, соединенных параллельно, определяется формулой:
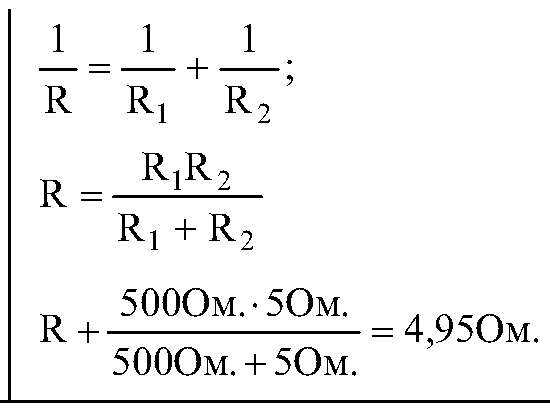
Заметим, что общее сопротивление двух параллельных резисторов всегда меньше, чем сопротивление меньшего из них. Общее сопротивление двух параллельно соединенных резисторов, имеющих одинаковое сопротивление, равно половине сопротивления одного из них.
Параллельное соединение трех и более резисторов
В общем случае общее сопротивление произвольного числа резисторов, соединенных параллельно, можно определить по формуле выше.
Пример 4
Определить общее сопротивление схемы, изображенной на рис. 1.11(а).
Решение
R1 и R2 соединены последовательно и их общее сопротивление RТ1 = R1 + R2 = 6 + 8 = 14 Ом.
Теперь, после замены резисторов R1 и R2 их общим сопротивлением RТ1, (схема на рис. 1.11(б)), резистор R3 оказался включенным параллельно с RТ1, равным ему по величине. Следовательно, их общее сопротивление RТ2 вполовину меньше каждого из них. Теперь схема примет вид, как показано на рис. 1.11(в), где RТ2 = 7 Ом и соединено последовательно с R4. Отсюда общее сопротивление схемы между точками А и В равно RТ2 + R4 = 7 + 3 = 10 Ом
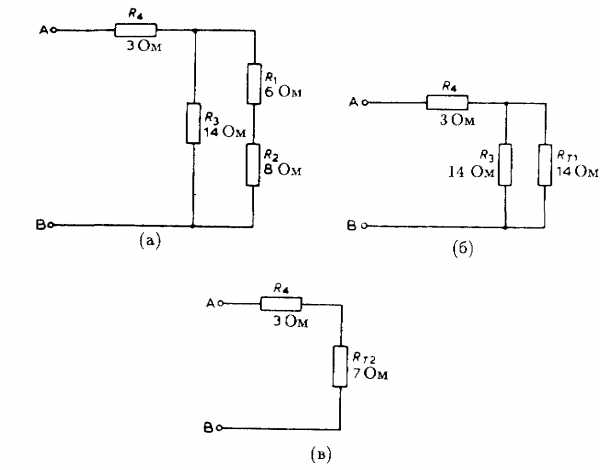
Рис. 1.11
radiolubitel.net
Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.
Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
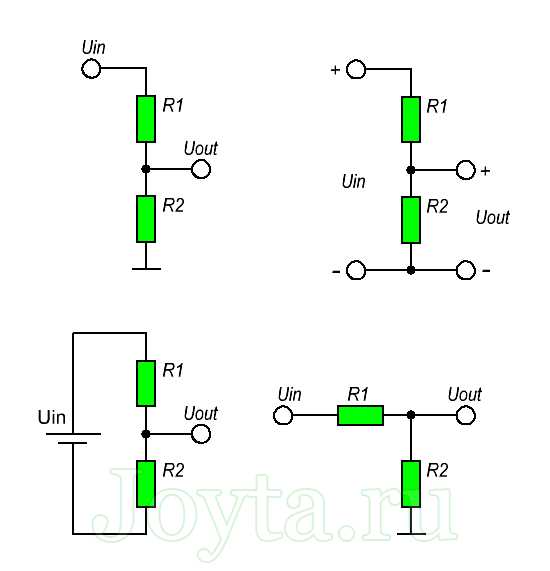Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.
Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.
Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:
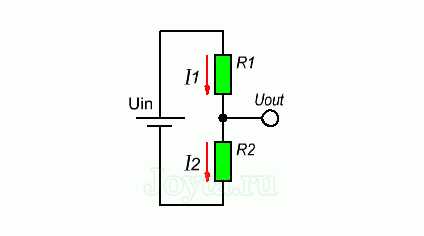Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:
Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:
Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:
И, на какое-то время, мы можем упростить схему:
Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:
А так как I1 равно I2, то:
Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.
Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.
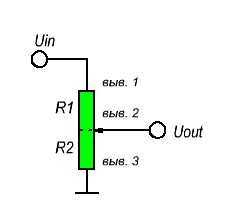
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.
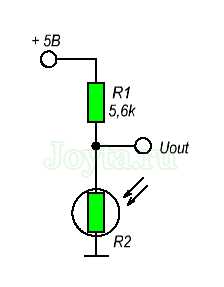
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.
www.joyta.ru
Делитель напряжения это цепь или схема соединения резисторов, применяемая для получения разных напряжений от одного источника питания.
Рассмотрим цепь из двух последовательно соединенных резисторов с разными сопротивлениями (рис. 1).
Рисунок 1. Последовательная цепь есть простейший делитель напряжения.
Согласно закону Ома если приложить к такой цепи напряжение, то падение напряжения на этих резисторах будет тоже разным.
UR1=I*R1;
UR2=I*R2.
Схема, изображенная на рисунке 1, и есть простейший делитель напряжения на резисторах . Обычно делитель напряжения изображают, как это показано на рисунке 2.
Рисунок 2. Классическая схема делителя напряжения.
Для примера разберем простейший делитель напряжения, изображенный на рисунке 2. В нем R1 = 2 кОм, R2 = 1 кОм и напряжение источника питания, оно же и есть входное напряжения делителя Uвх = 30 вольт. Напряжение в точке А равно полному напряжению источника, т. е. 30 вольт. Напряжение Uвых, то есть в точке В равно напряжению на R2.Определим напряжение Uвых.
Общий ток в цепи равен:
(1)
Для нашего примера I=30 В/ (1 кОм + 2 кОм) = 0,01 А = 10 мА.
Напряжение на R2 будет равно:
(2)
Для нашего примера UR2 = 0,01 А*1000 Ом = 10 В.
Выходное напряжение можно вычислить вторым способом, подставив в выражение (2) значение тока (1), тогда получим:
(3)
UR2 = 30 В*1 кОм/(1 кОм + 2 кОм) = 10 В.
Второй способ применим для любого делителя напряжения, состоящего из двух и более резисторов, включенных последовательно. Напряжение в любой точке схемы можно вычислить с помощью калькулятора за один прием, минуя вычисление тока.
Если делитель напряжения состоит из двух одинаковых резисторов, то приложенное напряжение делится на них пополам.
Uвых = Uвх/2
На рисунке 3 изображен делитель напряжения, состоящий из трех одинаковых резисторов сопротивлением в 1 кОм каждый. Вычислим напряжение в точках А и В относительно точки Е.
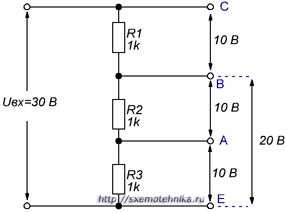
Рисунок 3. Делитель напряжения из трех резисторов.
Общее сопротивление R= R1+R2+R3 = 1 кОм + 1 кОм + 1 кОм = 3 кОм
Напряжение в точке А относительно точки Е будет равно:
Тгда Ua-e =30 В/(1 кОм + 1 кОм + 1 кОм)*1 кОм = 10 В.
Напряжение в точке В относительно точки Е будет равно:
Тгда Ub-e =30 В/(1 кОм + 1 кОм + 1 кОм)*(1 кОм + 1 кОм) = 20 В.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
www.sxemotehnika.ru
Общий провод (земля, корпусной провод) – это обозначение точки, потенциал которой принимается за ноль. В се остальные потенциалы и напряжения измеряются относительно этого потенциала, то общего провода.
Все открытые токоведущие части приборов и цепей обычно заземлены с помощью защитного заземляющего устройства, которое подключается к общему проводу приборов. Таким образом, между этими приборами не может возникнуть разность потенциалов, и не будет течь опасный для жизни ток.
На рисунке 1. показано, как на силовом распределительном щите все приборы соединены общей нулевой точкой с помощью толстых медных проводов на медную шину, которая соединена с заземлителем вкопанным в землю. Это и есть общий провод схемы.
Рисунок 1.Общий провод в распределительном щите.
Заземлитель или заземляющее устройство защищает человека от поражения электрическим током.
Заземление используется так же в автомобилях. В этом случае в качестве общего провода используется шасси. Если заглянуть под капот автомобиля, то вы увидите, как минусовой провод аккумулятора подключен прямо к раме авто (рис 2.).
Рисунок 2. Общий провод в автомобиле.
Это и есть земля или общий провод электрооборудования автомобиля.
Еще раз повторим, что земля это точка цепи, потенциал которой принимается за ноль и относительно этой точки измеряются все напряжения.
В электронном оборудовании металлический корпус или шасси также служит общим проводом или землей.
В небольших электронных схемах, выполненных на печатных платах, которые размещаются в пластмассовом корпусе, общим земляным проводом является медная подложка. Так же общие корпусные проводники на печатных платах обычно выполняются как можно с большей площадью (рис 3).
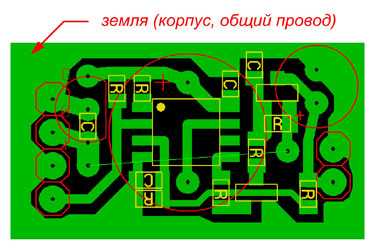
Рисунок 3. Общий провод на печатной плате.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
www.sxemotehnika.ru
5 правильных ответов на 6 вопросов(класс,хоть в одном наврать можно.Вот спасибо )и,наверно, прошивочка наша,товарищи.
Мужчины,помогите. пожалуйста
Тест.
1.Что изображено на картинке?
а)обрывник
б)пусковой элемент
в)разрядник
г)дроссель
2.Лампочка загорится если замкнуть точки:
а)1-2
б)3-4
в)1-3
г)загорится для каждого из вариантов
3.Определить напряжение в точке А относительно общего провода:
4.Какой тип корпуса у данной микросхемы?
5.Расположить правильно элементы стабилизатора:
6. Браслет надеваемый на руку при ремонте выполняет функцию:
а)фиксирует руку монтажника для уменьшения колебаний при монтаже-демонтаже
б)указывает на тип выполняемых работ
в)имеет медицинскую функцию
г)снимает статический заряд с тела
Часовой пояс: UTC + 5 часов
Сейчас, в связи с более — менее определившейся начинкой моего робота, и желанием привести все в нормальный вид, собрав все в единую конструкцию, озаботился его системой питания. Для чего и решил выделить отдельную тему.
Пока только все начиналось (несколько лет уже назад), и потребление было незначительным, из модулей — только ходовой да бамперы, а ассортимент доступных мне батарей — невелик.
На то время (2007г), оптимальными оказались свинцовые аккумуляторы 12v 1,3Ач.
Panasonic LC-V12 1R3PJ , 98×52(56)x46мм 580гр. Покупал по 4 бакса.
Также были 6-вольтовые, тоже 1,3Ач, по габаритам — примерно в половину толщины 12-вольтового.
SOLOMON SL-M613 6V1.3AH 98×52(56)x25мм 305гр.
HUAYU 6V1.3AH 98×52(56)x25мм 313гр.
Цена почти такая же (около 5 баксов).
Поскольку у меня ходовые движки — ДПМ-25-Н1-07Т , 27V,
При 27V — по паспорту:
В реальности, при питании от 12v, получилось:
При установке в роботе весом
2 КГ, с колесами D=78мм, и питании через драйвер L293 c ШИМ 1КГц нормально бегает при 120-150мА на движок.
Для нормальной нагрузки на ведущие колеса батарея весом около 600Г размещалась в коробке робота возле движков.
Несомненными преимуществами свинцовых аккумуляторов являются их неприхотливость, простые режимы заряда, отсутствие эффекта памяти, что позволяет использовать частичные режимы подзаряда, в том числе и сравнительно большими токами.
Сейчас появились вполне дешевые, а главное — доступные (появился модельный магазин в моем городе), литиевые батареи. Несмотря на более сложное обращение с ними и более высокую опасность при несоблюдении требований, они все же имеют много преимуществ.
Главные из которых — большая удельная емкость, возможность работы при больших токах, возможность быстрого (20-30 минут — до 100% емкости!) заряда большими токами. Так же — отсутствие эффекта памяти, возможность нормально работать при частичных подзарядах.
Что вполне компенсирует некоторые неудобства и более высокую, чем у свинцовых, стоимость.
Кроме того, появление в составе робота платы ЦК довольно большого размера, делает желательным уменьшение высоты батареи, чтобы не увеличивать высоту корпуса.
Если движки в корпусе занимают всего около 30мм высоты вместе с ред
art-lus.ru
Схема основного не инвертирующего включения приведена на рис.85.
Как видно из схемы сохранилась цепь отрицательной обратной связи. Но левый по схеме вывод входного резистора R1 подключен к общему проводу, а входное напряжение подается на неинвертирующий вход. Выполним вывод уравнения для определения выходного напряжения.
Определим напряжение в точке а. Ua = U¯ = (Uвых*R1)/(R0 + R1). Напряжение на неинверти рующем входе равно входному напряжению U+ = Uвх. Рассмотрим основное уравнение операционного усилителя Uвых = Ку*( U+ — U¯). Если правую и левую части уравнения поделим на Ку, то получим Uвых / Ку = (U+ — U¯) → 0. Это близко к истине, так как Ку величина большая и теоретически стремиться к бесконечности, Uвых конечна и не может быть больше напряжения питания. Отсюда получаем U+ = U¯, Uвх = (Uвых*R1)/(R0 + R1). Полученное выражение разрешим относительно выходного напряжения . В данном случае коэффициент передачи Ксос = (R0 + R1)/R0, и не может быть меньше единицы.
Выходное сопротивление схемы определяется также как и в предыдущей схеме.
Входное сопротивление схемы значительно больше, чем в предыдущем случае, так как оно определяется входным током операционного усилителя. Если используется ОУ 140УД7 с входным током 200нА, то при Uвх = 10в получим Rвхос = 10В/200нА = 50 мегом.
Модификацией основного не инвертирующего включения является схема без резистивной цепи обратной связи показанная на рис.83.
Эта схема характеризуется тем, что:
— для нее выполняется соотношение Uвых = Uвх, т.е. она является повторителем напряжения,
-она имеет высокое входное сопротивление,
-она имеет низкое выходное сопротивление.
В соответствии с указанными особенностями эта схема часто используется в качестве преобразователя импеданса (полного сопротивления).
Выводы основных соотношений для включений ОУ выполнены на постоянном токе (с целью упрощения), однако полученные результаты могут быть распространены и на частотную область. Для частотной области будем иметь:
— инвертирующее включение ,
— не инвертирующее включение .
Приведенные выражения позволяют просто получить выражения передаточных функций , которые подтверждают ранее полученный вывод о том, что при использовании усилителей с большим коэффициентом усиления передаточная функция определяется цепь обратной связи.
Передаточные функции будут иметь вид
— для инвертирующего включения ,
— для не инвертирующего включения .
Следовательно, если известна схема цепи обратной связи, то можно определить полные сопротивления и передаточную функцию.
Решающие элементы аналоговых вычислительных машин (АВМ).
Под решающими элементами будем понимать электронные устройства, предназначенные для выполнения вычислительных операций над переменными АВМ и построенные с применением ОУ.
Необходимость применения ОУ обоснована тем, что только большое значение коэффициента усиления (десятки, сотни тысяч) позволяет определить передаточную функцию только цепью обратной связи. Причем обратная связь должна быть отрицательной для получения устойчивой работы.
Сумматор.
Сумматор – решающий элемент, выполняющий операцию суммирования. Схема сумматора показана на рис.87. По известной методике сделаем вывод зависимости выходного напряжения в зависимости от входных напряжений.
обобщая полученный результат для схемы с N входами, будем иметь . Как видно из выражения выходное напряжение для такой схемы равно сумме произведений входных напряжений на коэффициент определяемый отношением сопротивления обратной связи и входным сопротивлением. Если выбрать все резисторы равными между собой, то все коэффициенты станут равными 1 и схема будет выполнять операцию суммирования. Если оставить один вход и коэффициент сделать равным 1, то получаем схему описываемую выражением Uвых = — Uвх. Получили схему, изменяющую знак входного напряжения – инвертор.
Интегратор.
Если в схеме сумматора резистор обратной связи R01 заменить на конденсатор, то получаем новый решающий элемент, выполняющий операцию интегрирования – интегратор (рис.88). Определим зависимость между входным и выходным напряжениями. Для достижения этой цели составим уравнение по первому закону Кирхгофа для точки a. При этом будем считать, что резистор и конденсатор выбраны таким образом, что ток протекающий через них значительно (например, в 1000 раз) больше входного тока операционного усилителя. Это дает нам возможность сделать допущение – пренебречь входным током операционного усилителя. При выводе воспользуемся законом Ома для участка цепи.
. В этом уравнении не определена переменная Ua. Для ее определения воспользуемся основным уравнением операционного усилителя . В зтом выражении , и, следовательно, Ua = -Uвых/Ку. Выходное напряжение всегда величина конечная, не превышающая напряжение питания, а коэффициент усиления Ку величина большая в пределе стремящаяся к бесконечности, и, следовательно, будем иметь Ua = — Uвых/(Ку → ∞) = → 0. Выполняя подстановку и разрешая уравнение относительно выходного напряжения, получаем . Полученное уравнение показывает, что выходное напряжение интегратора равно интегралу от входного умноженного на постоянный коэффициент 1/(R1C0). Учитывая, что у интегратора можно организовать несколько входов и предварительно зарядить конденсатор обратной связи общее уравнение будет иметь вид . Интегратор имеющий несколько входов называют – интегросумматор. Предварительный заряд конденсатора обратной связи используют для задания начальных условий.
Дифференциатор.
Если в схеме интегратора резистор и конденсатор поменять местами, то получим элемент выполняющий операцию дифференцирования – дифференциатор (рис.).
Составляя уравнение по первому закону Кирхгофа для точки а, получим . Принимая допущения сделанные при выводе уравнения интегратора, и разрешая уравнение относительно выходного напряжения получаем уравнение описывающее дифференциатор. , уравнение показывает, что данная схема выполняет операцию дифференцирования входного напряжения. В связи с высокой чувствительностью дифференциатора к импульсным помехам применение его ограничено.
Рассмотренные решающие элементы являются основными и позволяют решать с их использованием дифференциальные уравнения. Поэтому далее рассмотрим, как же можно решать дифференциальные уравнения. Для простоты понимания покажем это на примере.
infopedia.su
Провода в электрических схемах
До сих пор мы с вами анализировали электрические цепи (состоящие из одной батареи и одного сопротивления) без учета проводов, соединяющих компоненты этих цепей и формирующих полную схему. И вот тут-то, когда мы вспомнили про провода, сразу навязывается вопрос: а как их длина и форма прокладки повлияют на все наши вычисления? Чтобы выяснить это, давайте посмотрим на пару конфигураций электрических схем:
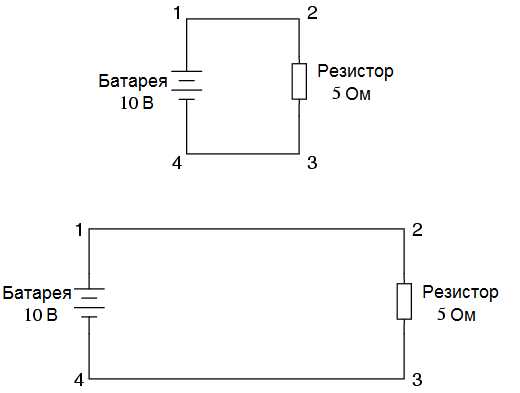
При разработке и анализе электрических схем на бумаге, мы обычно считаем что провода, соединяющие компоненты этих схем, имеют очень незначительное сопротивление, которое не оказывает заметного влияния на общее сопротивление схемы. Поэтому единственное сопротивление, с которым мы считаемся, это сопротивление электронных компонентов (радиодеталей). В приведенных выше схемах сопротивление (величиной 5 Ом) порождается только резисторами, и только это сопротивление мы будем учитывать во всех наших расчетах. В реальности, металлические провода действительно обладают некоторым сопротивлением, но его величина намного меньше сопротивления других компонентов схемы, в связи с чем мы со спокойной совестью можем его игнорировать. Исключение из этого правила составляет силовая электропроводка, где даже небольшое сопротивление провода может создать значительное падение напряжения.
Если сопротивление соединительного провода очень мало или вовсе отсутствует, мы можем рассматривать соединяемые им точки схемы как электрически общие. То есть, точки 1 и 2 в приведенных выше схемах могут быть непосредственно соединены между собой, а могут отстоять друг от друга на расстоянии длины соединяющего их провода, и это не будет влиять на величины напряжения и сопротивления, измеряемых по отношению к этим точкам. То же самое относится и к точкам 3 и 4. Это означает, что вы можете перерисовать любой провод на схеме так, как вам будет удобно, или при необходимости укоротить или удлинить провода в реальной схеме без заметного воздействия на ее функции.
Величина напряжения, измеряемого между наборами «электрически общих» точек, будет одинакова. То есть, напряжение между точками 1 и 4 (на контактах батареи) будет таким же, как и напряжение между точками 2 и 3 (на выводах резистора). Теперь внимательно посмотрите на следующую схему, и попытайтесь определить, какие точки здесь будут электрически общими:
Эта схема, не считая проводов, содержит два компонента: батарею и резистор. Несмотря на то, что провода при формировании облика схемы принимают замысловатый путь, мы можем увидеть две группы электрически общих точек. Общими по отношению друг к другу здесь являются точки 1,2,3, потому что они связаны одним проводом, и точки 4,5,6, которые связаны между собой другим проводом.
Напряжение между точками 1 и 6 составляет 10 В, это напряжение на клеммах батареи. В связи с тем, что точки 4 и 5 являются электрически общими по отношению к точке 6, а точки 2 и 3 — по отношению к точке 1, напряжение между любыми двумя точками этих групп так же будет равно 10 вольтам:
Напряжение между точками 1 и 4 = 10 вольт
Напряжение между точками 2 и 4 = 10 вольт
Напряжение между точками 3 и 4 = 10 вольт (напряжение на резисторе)
Напряжение между точками 1 и 5 = 10 вольт
Напряжение между точками 2 и 5 = 10 вольт
Напряжение между точками 3 и 5 = 10 вольт
Напряжение между точками 1 и 6 = 10 вольт (напряжение батареи)
Напряжение между точками 2 и 6 = 10 вольт
Напряжение между точками 3 и 6 = 10 вольт
Теперь мы рассмотрим электрически общие точки. Так как эти точки связаны между собой одним проводом (имеющим нулевое сопротивление), то между ними не будет никакого напряжения, независимо от величины тока, проходящего по этому проводу от одной его точки до другой. Таким образом, если мы измерим напряжение между этими точками, то оно будет равно нулю:
Напряжение между точками 1 и 2 = 0 вольт Точки 1, 2, и 3 являются
Напряжение между точками 2 и 3 = 0 вольт электрически общими
Напряжение между точками 1 и 3 = 0 вольт
Напряжение между точками 4 и 5 = 0 вольт Точки 4, 5, и 6 являются
Напряжение между точками 5 и 6 = 0 вольт электрически общими
Напряжение между точками 4 и 6 = 0 вольт
Нулевые значения напряжения можно подтвердить математическими расчетами. При напряжении батареи 10 вольт и сопротивлении резистора 5 Ом, сила тока в нашей цепи будет равна 2 амперам. Так как провод имеет нулевое сопротивление, то падение напряжение между двумя любыми его точками по Закону Ома будет равно:
Из этого уравнения видно, что напряжение между двумя точками одного провода, обладающего нулевым сопротивлением, вне зависимости от величины тока равно нулю. (Результатом умножения любого числа на ноль, всегда будет ноль).
В связи с тем, что электрически общие точки при измерениях показывают одинаковые значения напряжения и сопротивления, провода, соединяющие эти точки, очень часто имеют одинаковые обозначения:
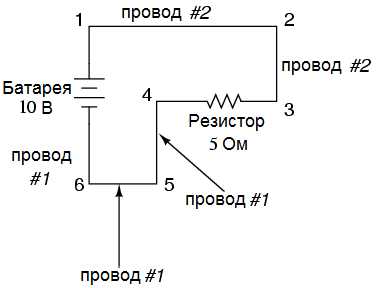
В этой схеме точки 1, 2 и 3 являются электрически общими, поэтому провод соединяющий точки 1 и 2 (провод #2) имеет такое же обозначение, как и провод соединяющий точки 2 и 3 (провод #2). В реальной цепи, провод соединяющий точки 1 и 2 может отличаться по цвету и размеру от провода, соединяющего точки 2 и 3, но оба эти повода будут иметь одинаковое обозначение. То же самое касается и проводов, соединяющих точки 6, 5 и 4.
Знание того, что между электрически общими точками напряжение всегда равно нулю, может помочь вам в поиске неисправностей схемы. Если вы уверены, что измеряете напряжение между электрически общими точками, а прибор показывает напряжение отличное от нуля, то между этими точками существует обрыв провода.
Примечание: в подавляющем большинстве практических случаев, мы с вами можем считать, что провода обладают нулевым сопротивлением на всем своем протяжении. В действительности, если провода не являются сверхпроводимыми, то они обладают небольшим сопротивлением. Зная это, мы должны иметь в виду, что принципы электрически общих точек действительны в значительной степени, но не абсолютно. То есть, правило, согласно которому электрически общие точки имеют нулевое напряжение между собой, можно сформулировать поточнее: между электрически общими точками существует очень маленькое напряжение. Такое напряжение практически неизбежно вследствие того, что небольшая величина сопротивления соединительного провода не может не породить небольшое напряжение при прохождении тока по этому проводу. Теперь, когда вы понимаете, что правила основываются на идеальных условиях, вы не будете озадачены, если столкнетесь с некоторыми условиями, кажущимися исключением из правил.
Краткий обзор:
Соединительные провода в цепи, как предполагается, имеют нулевое сопротивление, если не указано иное.
Провода в схеме можно укоротить или удлинить, и это не повлияет на ее функционирование.
Точки цепи, непосредственно связанные между собой проводом с нулевым сопротивлением, называются электрически общими.
Напряжение между электрически общими точками, вне зависимости от величины тока, будет равно нулю (в идеале).
Напряжение или сопротивление между группами электрически общих точек будет одинаково.
Все эти правила описывают идеальные условия, где предполагается, что соединительные провода имеют абсолютно нулевое сопротивление. В реальности дела обстоят не совсем так. Чтобы эти правила выполнялись, провода должны обладать очень маленьким сопротивлением.
www.radiomexanik.spb.ru