8-900-374-94-44
Все типы используемых АЦП можно разделить по признаку измеряемого значения напряжения на две группы: АЦП мгновенных значений напряжения и АЦП средних значений напряжения (интегрирующие АЦП).
АЦП мгновенных значений можно разделить на следующие основные виды: последовательного счета, последовательного приближения, параллельные, параллельно-последовательные и с промежуточным преобразованием в интервал времени.
Структурная схема АЦП последовательного счета приведена на рис. 7 а. Она содержит компаратор, при помощи которого выполняется сравнение входного напряжения с напряжением обратной связи. На прямой вход компаратора поступает входной сигнал uвх, а на инвертирующий — напряжение u5 обратной связи. Работа преобразователя начинается с приходом импульса «ПУСК» от схемы управления (на рисунке она не показана), который замыкает ключ
Когда выходное напряжение ЦАП сравняется с входным напряжением, произойдет переключение компаратора и по его выходному сигналу «СТОП» разомкнется ключ S. В результате импульсы от генератора перестанут поступать на вход счетчика. Выходной код, соответствующий равенству ивх = и5, снимается с выходного регистра счетчика.
Графики, иллюстрирующие процесс преобразования напряжения в цифровой код, приведены на рис. 7 б. Из этих графиков видно, что время преобразования переменное и зависит от уровня входного сигнала. При числе двоичных разрядов счетчика, равном п, и периоде следования счетных импульсов Т максимальное время преобразования можно определить по формуле:
(7)
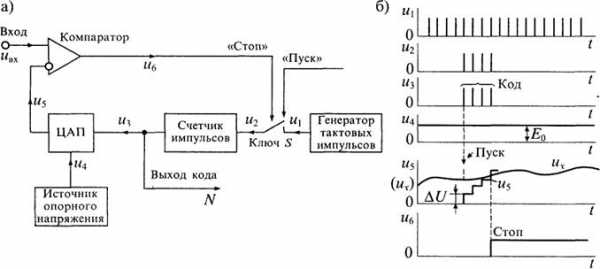
Рис. 7. Структурная схема АЦП последовательного счета (а) и графики процесса преобразования (б)
Так, например, при п = 10 разрядов и T = 1мкс (т.е. при тактовой частоте 1 МГц) максимальное время преобразования равно
что обеспечивает максимальную частоту преобразования около 1 кГц.
Уравнение преобразования АЦП последовательного счета можно записать в виде:
где 0 ≤ k ≤ n — число ступеней до момента сравнения, ∆
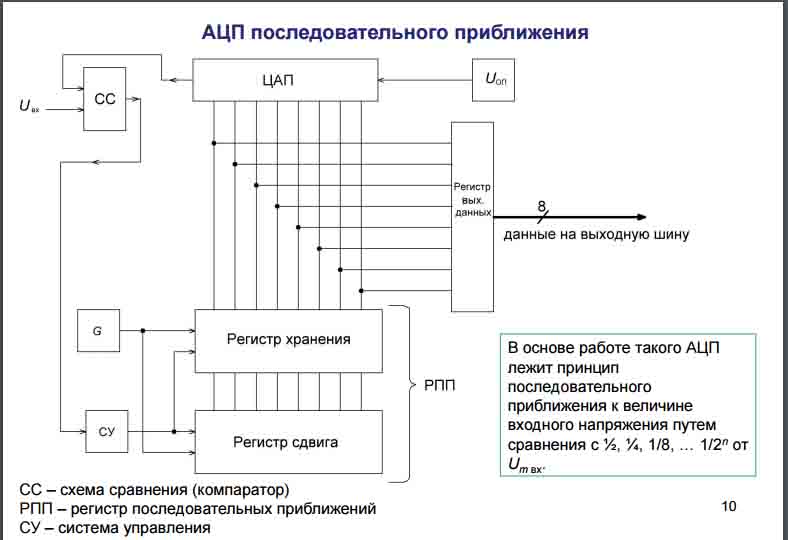
Структурная схема АЦП последовательного приближения приведена на рис. 8 а. По сравнению со схемой АЦП последовательного счета в ней сделано одно существенное изменение — вместо счетчика введен регистр последовательного приближения (РПП). Это изменило алгоритм уравновешивания и сократило время преобразования.
В основе работы АЦП с РПП лежит принцип дихотомии, т. е. последовательного сравнения преобразуемого напряжения uВХ с 1/2, 1/4, 1/8 и т. д. возможного максимального его значения Это позволяет для n-разрядного АЦП выполнить весь процесс преобразования за п последовательных шагов приближения (итераций) вместо (2n-1) при использовании последовательного счета и получить существенный выигрыш в быстродействии. График процесса преобразования АЦП с РПП показан на рис. 8 б.
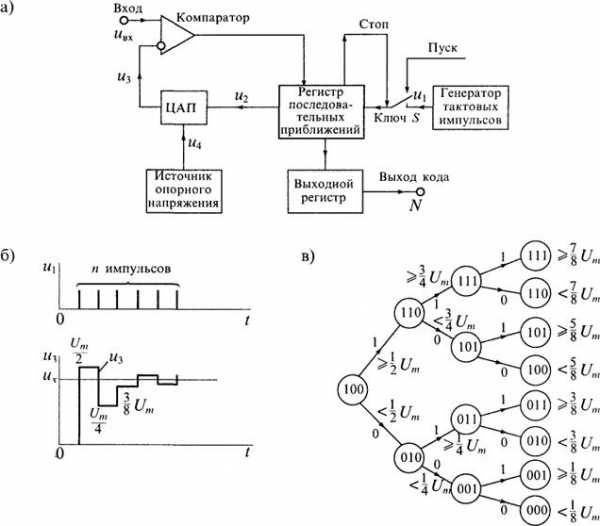
Рис. 8. Структурная схема АЦП последовательного приближения (а), графики процесса преобразования (б) и диаграмма последовательности переходов для трехразрядного АЦП (в)
В качестве примера на рис. 8 в показана диаграмма переходов для трехразрядного АЦП последовательного приближения. Поскольку на каждом шаге производится определение значения одного разряда, начиная со старшего, то такой АЦП часто называют АЦП поразрядного уравновешивания. При первом сравнении определяется — больше или меньше напряжение uBX, чем Um/2 На следующем шаге определяется, в какой четверти диапазона находится uвх. Каждый последующий шаг вдвое сужает область возможного результата.
При каждом шаге сравнения компаратор формирует импульсы, соответствующие состоянию «больше-меньше» (1 или 0), управляющие регистром последовательных приближений.
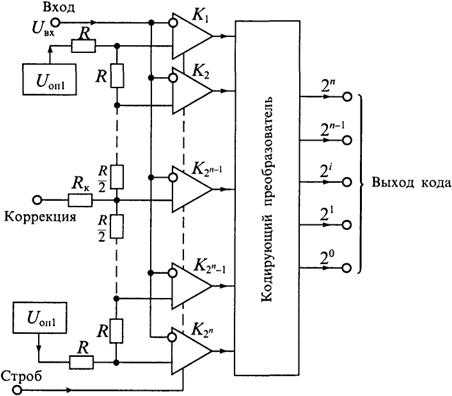
Рис. 9. Структурная схема параллельного АЦП
Для преобразования унитарного кода в двоичный (или двоично-десятичный) используют кодирующий преобразователь. При работе в двоичном коде все резисторы делителя имеют одинаковые сопротивления R. Время преобразования такого преобразователя составляет один такт, т. е. Тпр = Т. Параллельные преобразователи являются в настоящее время самыми быстрыми и могут работать с частотой дискретизации свыше 100МГц. Для получения более широкой полосы пропускания компараторы обычно делают стробируемыми.
Делитель опорного напряжения представляет собой набор низкоомных резисторов с сопротивлением около 1 Ом. По выводу «Коррекция» возможно проведение коррекции напряжения смещения нулевого уровня на входе, а по выводу Uon2 — абсолютной погрешности преобразования в конечной точке шкалы. Номинальные значения опорных напряжений имеют значения: Uon1 =-0,075 …0В, и Uon2 = — 2,l …-1,9В. Типовая задержка срабатывания компараторов около 7нс.
studfiles.net
Параллельные АЦП (их ещё называют ПНК считывания) представляют собой группу параллельно-включенных компараторов.
Аналоговый входной сигнал Uвх прикладывается ко всем компараторам одновременно. Один из входов каждого компаратора подключается к собственному опорному напряжению.
Значения опорных напряжений компараторов отличаются друг от друга на напряжение, соответствующее младшему двоичному разряду.
Все компараторы, для которых Uвх > Uоп изменяют состояние своих входов после подключения Uвх. Остальные компараторы, для которых Uвх < Uоп не меняют свое состояние. Выходы компараторов подключены к декодирующей схеме, которая преобразует совокупность состояний компараторов, после приложения Uвх в позиционный двоичный код.
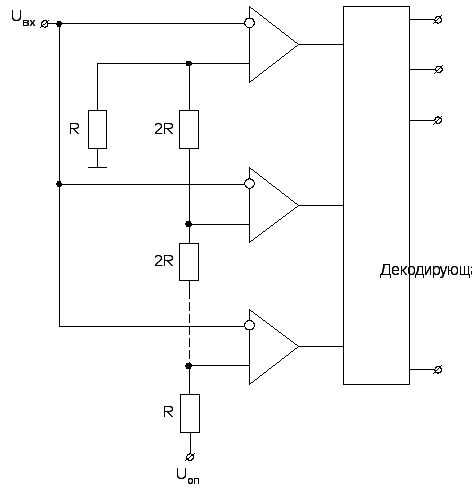
Рис. 132. Структурная схема АЦП параллельного действия
Для уяснения работы данного АЦП рассмотрим двухразрядный АЦП со схемой декодирования.
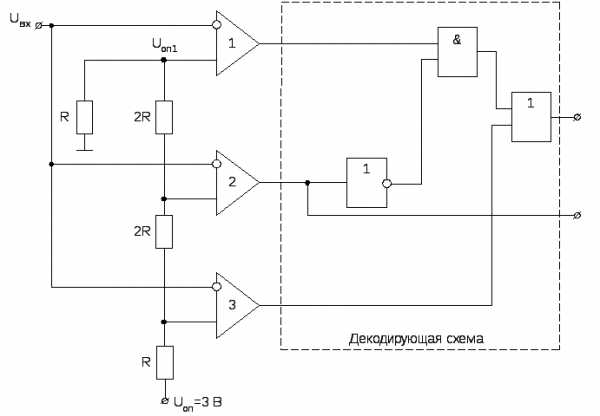
Рис. 133. Схема двухразрядного АЦП
Опорные напряжения, прикладываемые к компараторам, начинаются от значения Uоп1, равного половине младшего разряда.
Для двух разрядов необходимо компаратора. ЕслиUоп=3, то половина младшего разряда будет 0,5 В.
Далее значение Uоп каждого разряда увеличивается на величину двоичного веса.
Считаем
до 3, значит вес одного разряда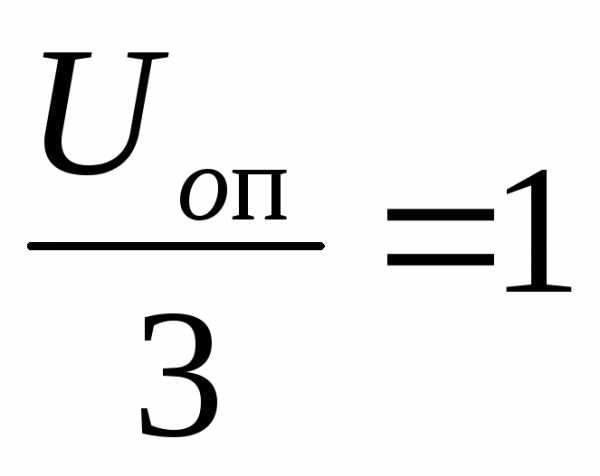 
В.
Для В,В.
Если Uвх < 0,5 В, то все выходы компараторов имеют низкий уровень и цифровой код будет 00.
Если 0,5 < Uвх < 1,5 В, то выход компаратора №1 приобретает высокий уровень, а выходы второго и третьего – низкий. Выход компаратора №2 после инвертирования поступает на схему совпадения, на первый вход которой поступает высокий уровень с компаратора №1 и высокий уровень со схемы совпадения через ИЛИ приводит к появлению кода 01.
Если 1,5 < Uвх < 2,5 В, то выход компаратора №2 приобретает высокий уровень, в выход «И» низкий, при этом код 10.
Если Uвх > 2,5 В, то выходы всех компараторов приобретают высокий уровень и код 11.
Основным достоинством схемы параллельного АЦП является высокое быстродействие (< 30 нс). Это объясняется тем, что цифровой код появляется практически сразу по истечении времени переключения компараторов. Но при этом имеет место разное время задержки для различных разрядов за счет разброса времени срабатывания компараторов и различного числа каскадов логических схем для различных разрядов.
Поэтому значения разрядных кодов передаются в выходной регистр кода по сигналу стробирования, с задержкой, необходимой для уверенного срабатывания всех компараторов и с учетом максимальной задержки на логических элементах.
Основной недостаток в том, что для реализации многоразрядного АЦП требуется очень большое количество оборудования:
,
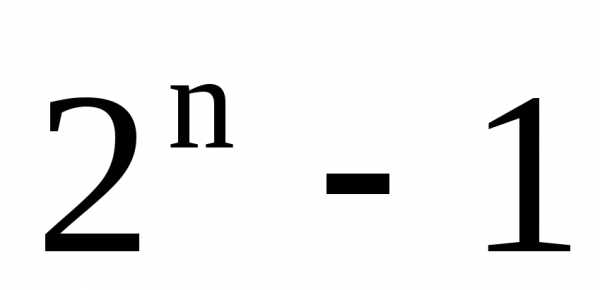еслиn
= 8, то
компараторов и надо формировать 255 опорных уровней и иметь громоздкую декодирующую схему.{1107ПВ1}.
Поразрядное взвешивание является наиболее распространенным методом аналого-цифрового преобразования.
Эти АЦП имеют достаточную скорость (для n-разрядного требуется n тактов) и не так .много оборудования. То есть в сравнении с быстродействующими (параллельными АЦП) и точными, но медленными (двухтактными интегрирующими АЦП) они как бы занимают промежуточное положение.
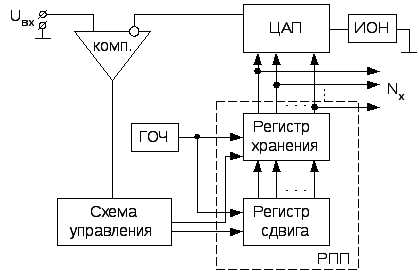
Рис. 134. Структурная схема и временные диаграммы работы АЦП
В данном преобразователе для формирования эталонных уровней напряжения используется ЦАП. В данном АЦП кодирование входного напряжения осуществляется путем последовательного сравнения его с суммой эталонных напряжений, формируемых ЦАП. Процесс кодирования похож на подбор гирь при взвешивании на весах, поэтому АЦП данного типа называют преобразователями взвешивания или АЦП последовательных приближений.
Преобразователь состоит из источника опорного напряжения (ИОН), генератора тактовых импульсов (ГОЧ), ЦАП, компаратора и регистра последовательных приближений. Регистр последовательных приближений (РПП) состоит из регистра хранения, регистра сдвига и схемы управления. В качестве РПП могут использоваться серийные микросхемы К155ИР7 на 12 разрядов или К564ИР13.
Преобразование
начинается с установки в «1» в старшем
разряде регистра хранения и «0» во все
остальные. ЦАП преобразует старший
разряд в аналоговое напряжение, равное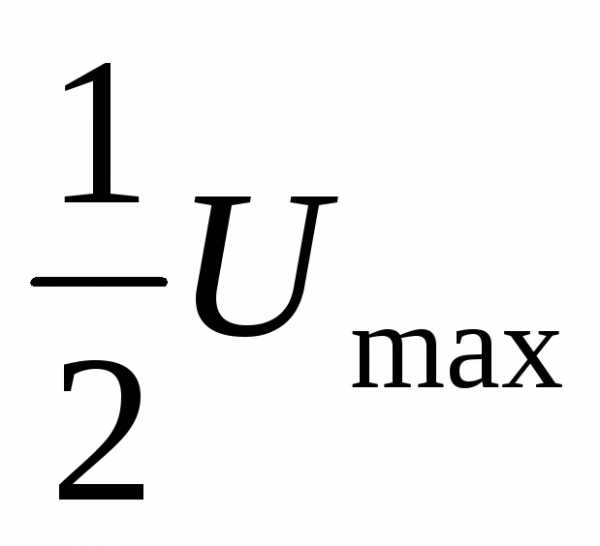 
или половине полной шкалыUоп.
Компаратор сравнивает выход ЦАП с аналоговым входным сигналом. Если входное напряжение больше, чем выходное ЦАП, то в ячейке старшего разряда сохраняется «1», в противном случае в этом разряде устанавливается «0».
Регистр
сдвига в начале следующего такта сдвигает
«1» в следующий младший разряд. Выходное
напряжение ЦАП при этом 
().
Если выходное напряжение ЦАП при этом меньше, чем Uвх, то в следующем разряде установится «1», в нашем примере Uвх < UЦАП, поэтому во втором разряде установится «0». Процесс продолжается до тех пор, пока не будут проверены все разряды.
Поэтому полное время преобразования n-разрядного АЦП пропорционально n тактам взвешивания. Кроме того, на считывание кода и подготовку к следующему циклу затрачивается еще один такт преобразования.
При реализации АЦП в интегральном исполнении длительность такта tгоч < 1 мкс.
Статическая ошибка АЦП определяется в основном точностью используемого ЦАП и компаратора.
При этом стандартным требованием по точности является следующее: ошибки, вносимые за счет погрешностей используемых элементов, не должны превышать половины младшего разряда кода, откуда можно и определить требования к погрешности регистров и ключей ЦАП, стабильности ИОН и чувствительности компаратора.
Так
для 10-ти разрядного АЦП с Umax = 10 В, можно найти, что относительные
погрешности РМ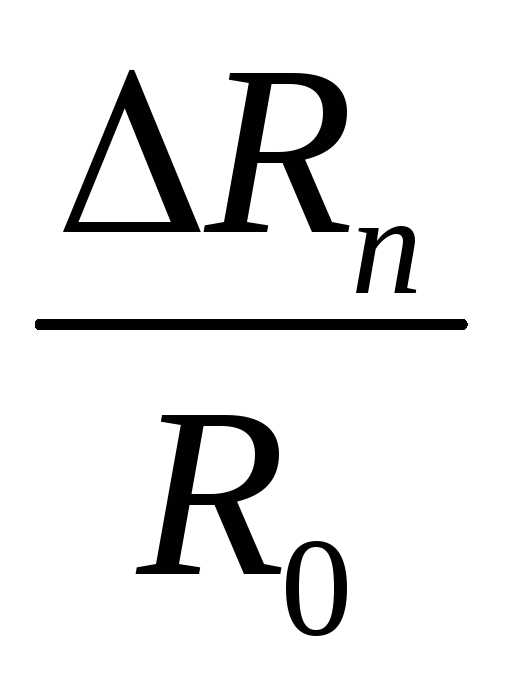 
и ИОН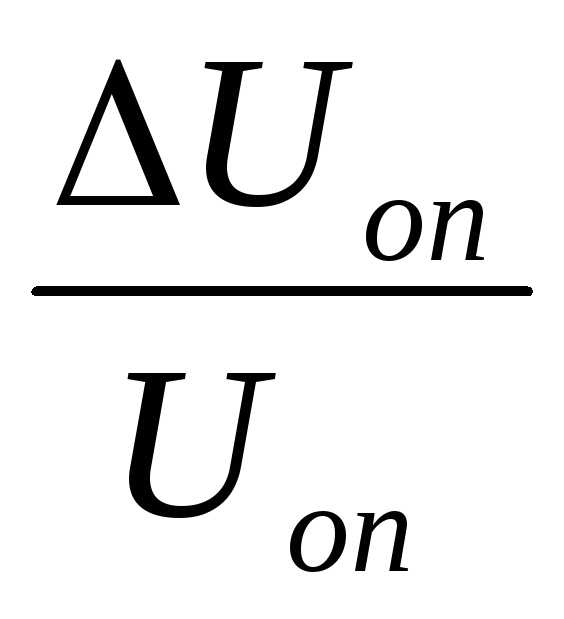
должны быть
,
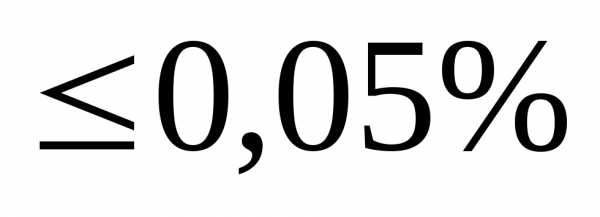а чувствительность компаратора
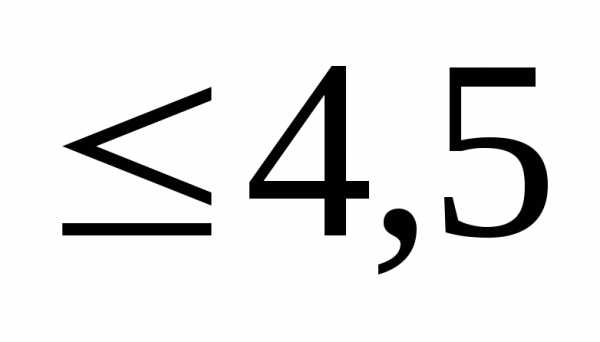мВ. В противном случае младшие разряды
кода будут не достоверны.
В случае, если за время преобразования входной сигнал может измениться более чем на половину младшего разряда, на вход АЦП необходимо включить устройство выборки и запоминания, иначе в преобразователе устанавливается такое напряжение на выходе ЦАП, которое не уравновешивает входной сигнал.№№
Преобразователи взвешивания могут обеспечивать точность до 0,005%, что соответствует 14 15 двоичным разрядам кода, при времени преобразования – единицы микросекунд.
Контрольные вопросы
1. Преимущества и особенности применения преобразователей слежения.
2. АЦП параллельного действия.
3. Принцип работы и особенности АЦП поразрядного кодирования.
studfiles.net
Аналогово-цифровой преобразователь (АЦП) — один из самых важных электронных компонентов в измерительном и тестовом оборудовании. АЦП преобразует напряжение (аналоговый сигнал) в код, над которым микропроцессор и программное обеспечение выполняют определенные действия. Даже если Вы работаете только с цифровыми сигналами, скорее всего Вы используете АЦП в составе осциллографа, чтобы узнать их аналоговые характеристики.
Существует несколько основных типов архитектуры АЦП, хотя в пределах каждого типа существует также множество вариаций. Различные типы измерительного оборудования используют различные типы АЦП. Например, в цифровом осциллографе используется высокая частота дискретизации, но не требуется высокое разрешение. В цифровых мультиметрах нужно большее разрешение, но можно пожертвовать скоростью измерения. Системы сбора данных общего назначения по скорости дискретизации и разрешающей способности обычно занимают место между осциллографами и цифровыми мультиметрами. В оборудовании такого типа используются АЦП последовательного приближения либо сигма-дельта АЦП. Существуют также параллельные АЦП для приложений, требующих скоростной обработки аналоговых сигналов, и интегрирующие АЦП с высокими разрешением и помехоподавлением.
На рис.1. показаны возможности основных архитектур АЦП в зависимости от разрешения и частоты дискретизации.
Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5Г (5*109) отсчетов/сек для стандартных устройств и 20Г отсчетов/сек для оригинальных разработок. Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10-ти разрядные версии.
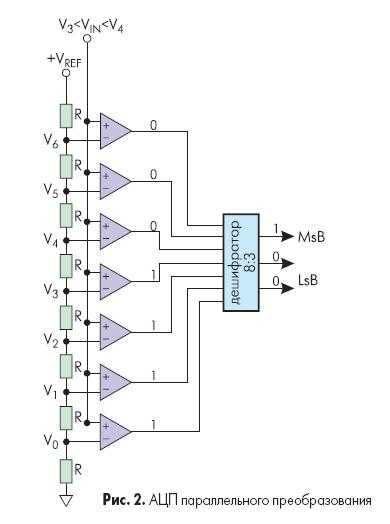
Рис. 2 показывает упрощенную блок-схему 3-х разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется). Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным VREF /23. В результате для 3-х разрядного АЦП требуется 23-1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (28-1)) компараторов.
С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рис. 2 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе «1», а верхние три компаратора — «0». Дешифратор преобразует (23-1) — разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код.
Параллельные АЦП — достаточно быстрые устройства, но они имеют свои недостатки. Из-за необходимости использовать большое количество компараторов параллельные АЦП потребляют значительную мощность, и их нецелесообразно использовать в приложениях с батарейным питанием.
Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 100К (1х103) до 1М (1х106) отсчетов/сек.
Рис. 3 показывает упрощенную блок-схему АЦП последовательного приближения. В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0, за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением.
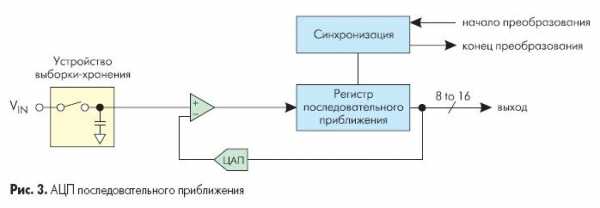
Например, для 8-разрядного АЦП последовательного приближения (рис. 4) выходы регистра при этом устанавливаются в «10000000». Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0. Это дает регистру последовательного приближения команду переключить свои выходы в состояние «01000000», что соответственно приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в «0», то выходы регистра переключились бы в состояние «00100000». Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение (рис. 4), и компаратор переключается в состояние логической 1. Это предписывает регистру последовательного приближения сохранить «1» во втором разряде и подать «1» на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования.
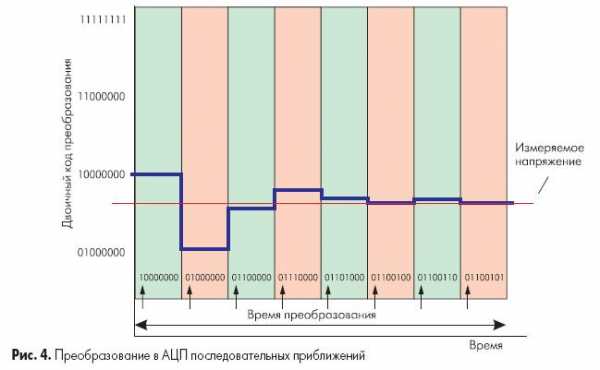
Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП. Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа.
Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100К отсчетов/сек, а при 24 разрядах эта частота падает до 1К отсчетов/сек и менее, в зависимости от устройства.
Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов.
Принцип работы сигма-дельта АЦП сложнее для понимания. Эта архитектура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8М отсчетов/сек.
Блок-схема сигма-дельта АЦП первого порядка приведена на рис. 5. Аналоговый сигнал подается на интегратор, выходы которого подсоединены к компаратору, который в свою очередь присоединен к 1-разрядному ЦАП в петле обратной связи. Путем серии последовательных итераций интегратор, компаратор, ЦАП и сумматор дают поток последовательных битов, в котором содержится информация о величине входного напряжения.
Результирующая цифровая последовательность затем подается на фильтр нижних частот для подавления компонентов с частотами выше частоты Котельникова (она составляет половину частоты дискретизации АЦП). После удаления высокочастотных составляющих следующий узел — дециматор — прореживает данные. В рассматриваемом нами АЦП дециматор будет оставлять 1 бит из каждых полученных 128 в выходной цифровой последовательности.
Так как внутренний цифровой ФНЧ в сигма-дельта АЦП представляет собой неотъемлемую часть для осуществления процесса преобразования, время установления ФНЧ становится фактором, который необходимо учитывать при скачкообразном изменении входного сигнала. Например, при переключении входного мультиплексора или при переключении предела измерения прибора необходимо подождать, пока пройдут несколько отсчетов АЦП, и лишь потом считывать корректные выходные данные.
Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП.
И последний тип АЦП, о котором пойдет здесь речь — АЦП двухтактного интегрирования. В цифровых мультиметрах, как правило, используются именно такие АЦП, т.к. в этих измерительных приборах необходимо сочетание высокого разрешения и высокого помехоподавления. Идея преобразования в таком интегрирующем АЦП гораздо менее сложна, чем в сигма-дельта АЦП.
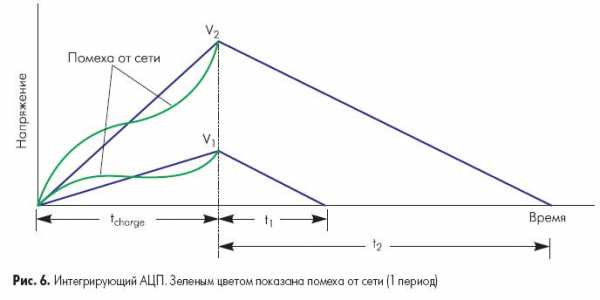
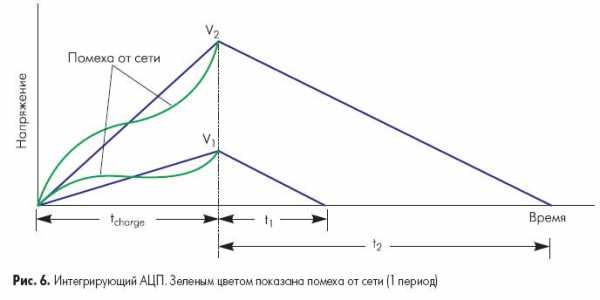
На рисунке 6 показан принцип работы АЦП двухтактного интегрирования. Входной сигнал заряжает конденсатор в течение фиксированного периода времени, который обычно составляет один период частоты питающей сети (50 или 60Гц) или кратен ему. При интегрировании входного сигнала в течение промежутка времени такой длительности высокочастотные помехи подавляются. Одновременно исключается влияние нестабильности напряжения сетевого источника питания на точность преобразования. Это происходит потому, что значение интеграла от синусоидального сигнала равно нулю, если интегрирование осуществляется во временном интервале, кратном периоду изменения синусоиды.
По окончании времени заряда АЦП разряжает конденсатор с фиксированной скоростью, в то время как внутренний счетчик подсчитывает количество тактовых импульсов за время разряда конденсатора. Большее время разряда, таким образом, соответствует большему значению показаний счетчика и большему измеряемому напряжению (рис.6).
АЦП двухтактного интегрирования имеют высокую точность и высокую разрешающую способность, а также имеют сравнительно простую структуру. Это дает возможность выполнять их в виде интегральных микросхем. Основной недостаток таких АЦП — большое время преобразования, обусловленное привязкой периода интегрирования к длительности периода питающей сети. Например, для 50 Гц — оборудования частота дискретизации АЦП двухтактного интегрирования не превышает 25 отсчетов/сек. Конечно, такие АЦП могут работать и с большей частотой дискретизации, но при увеличении последней помехозащищенность падает.
Существуют общие определения, которые принято использовать в отношении аналого-цифровых преобразователей. Тем не менее, характеристики, приводимые в технической документации производителей АЦП, могут показаться довольно путаными. Правильный же выбор оптимального по сочетанию своих характеристик АЦП для конкретного приложения требует точной интерпретации данных, приводимых в технической документации.
Наиболее часто путаемыми параметрами являются разрешающая способность и точность, хотя эти две характеристики реального АЦП крайне слабо связаны между собой. Разрешение не идентично точности, 12-разрядный АЦП может иметь меньшую точность, чем 8-разрядный. Для АЦП разрешение представляет собой меру того, на какое количество сегментов может быть поделен входной диапазон измеряемого аналогового сигнала (например, для 8-разрядного АЦП это 28=256 сегментов). Точность же характеризует суммарное отклонение результата преобразования от своего идеального значения для данного входного напряжения. То есть, разрешающая способность характеризует потенциальные возможности АЦП, а совокупность точностных параметров определяет реализуемость такой потенциальной возможности.
АЦП преобразует входной аналоговый сигнал в выходной цифровой код. Для реальных преобразователей, изготавливаемых в виде интегральных микросхем, процесс преобразования не является идеальным: на него оказывают влияние как технологический разброс параметров при производстве, так и различные внешние помехи. Поэтому цифровой код на выходе АЦП определяется с погрешностью. В спецификации на АЦП указываются погрешности, которые дает сам преобразователь. Их обычно делят на статические и динамические. При этом именно конечное приложение определяет, какие характеристики АЦП будут считаться определяющими, самыми важными в каждом конкретном случае.
В большинстве применений АЦП используют для измерения медленно изменяющегося, низкочастотного сигнала (например, от датчика температуры, давления, от тензодатчика и т.п.), когда входное напряжение пропорционально относительно постоянной физической величине. Здесь основную роль играет статическая погрешность измерения. В спецификации АЦП этот тип погрешности определяют аддитивная погрешность (Offset), мультипликативная погрешность (Full-Scale), дифференциальная нелинейность (DNL), интегральная нелинейность (INL) и погрешность квантования. Эти пять характеристик позволяют полностью описать статическую погрешность АЦП.
Передаточная характеристика АЦП — это функция зависимости кода на выходе АЦП от напряжения на его входе. Такой график представляет собой кусочно-линейную функцию из 2N «ступеней», где N — разрядность АЦП. Каждый горизонтальный отрезок этой функции соответствует одному из значений выходного кода АЦП (см. рис. 7). Если соединить линиями начала этих горизонтальных отрезков (на границах перехода от одного значения кода к другому), то идеальная передаточная характеристика будет представлять собой прямую линию, проходящую через начало координат.
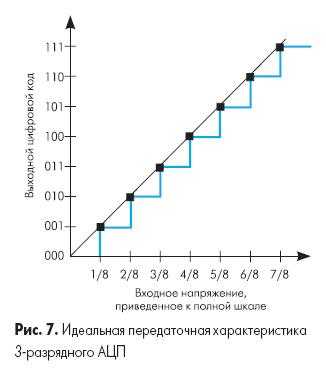
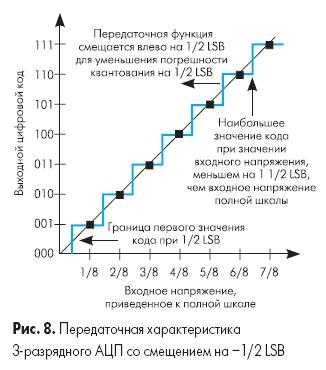
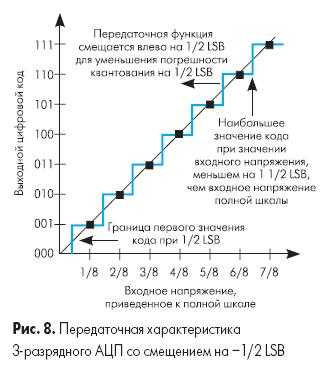
Рис. 7 иллюстрирует идеальную передаточную характеристику для 3-х разрядного АЦП с контрольными точками на границах перехода кода. Выходной код принимает наименьшее значение (000b) при значении входного сигнала от 0 до 1/8 полной шкалы (максимального значения кода этого АЦП). Также следует отметить, что АЦП достигнет значения кода полной шкалы (111b) при 7/8 полной шкалы, а не при значении полной шкалы. Т.о. переход в максимальное значение на выходе происходит не при напряжении полной шкалы, а при значении, меньшем на наименьший значащий разряд (LSB), чем входное напряжение полной шкалы. Передаточная характеристика может быть реализована со смещением -1/2 LSB. Это достигается смещением передаточной характеристики влево, что смещает погрешность квантования из диапазона -1… 0 LSB в диапазон -1/2 … +1/2 LSB.
Из-за технологического разброса параметров при изготовлении интегральных микросхем реальные АЦП не имеют идеальной передаточной характеристики. Отклонения от идеальной передаточной характеристики определяют статическую погрешность АЦП и приводятся в технической документации.
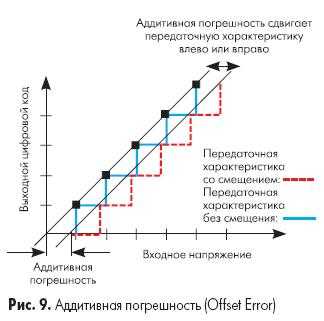
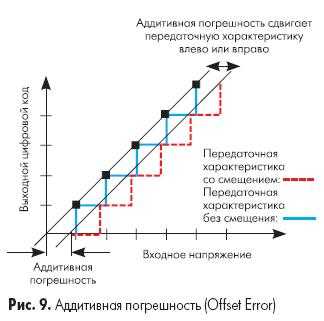
Идеальная передаточная характеристика АЦП пересекает начало координат, а первый переход кода происходит при достижении значения 1 LSB. Аддитивная погрешность (погрешность смещения) может быть определена как смещение всей передаточной характеристики влево или вправо относительно оси входного напряжения, как показано на рис.9. Таким образом, в определение аддитивной погрешности АЦП намеренно включено смещение 1/2 LSB.
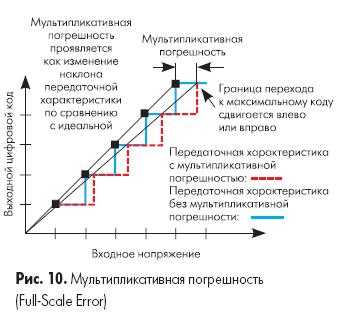
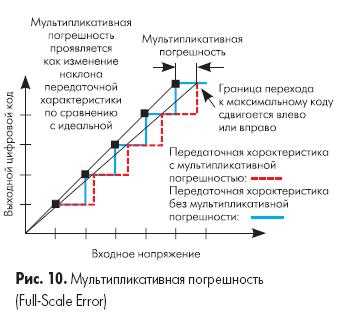
Мультипликативная погрешность (погрешность полной шкалы) представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии нулевой аддитивной погрешности (смещение отсутствует). Это проявляется как изменение наклона передаточной функции, что иллюстрирует рис. 10.
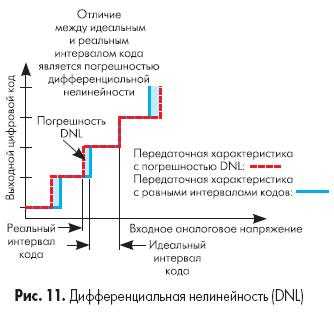
У идеальной передаточной характеристики АЦП ширина каждой «ступеньки» должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из 2N «ступеней» представляет собой дифференциальную нелинейность (DNL).
Величина наименьшего значащего разряда у АЦП составляет Vref/2N, где Vref — опорное напряжение, N — разрешение АЦП. Разность напряжений между каждым кодовым переходом должна быть равна величине LSB. Отклонение этой разности от LSB определяются как дифференциальная нелинейность. На рисунке это показано как неравные промежутки между «шагами» кода или как «размытость» границ переходов на передаточной характеристике АЦП.
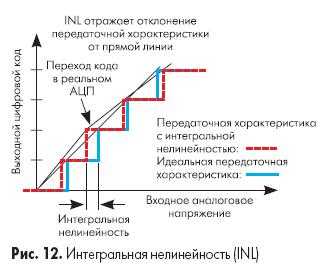
Интегральная нелинейность (INL) — это погрешность, которая вызывается отклонением линейной функции передаточной характеристики АЦП от прямой линии, как показано на рис. 12. Обычно передаточная функция с интегральной нелинейностью аппроксимируется прямой линией по методу наименьших квадратов. Часто аппроксимирующей прямой просто соединяют наименьшее и наибольшее значения. Интегральную нелинейность определяют путем сравнения напряжений, при которых происходят кодовые переходы. Для идеального АЦП эти переходы будут происходить при значениях входного напряжения, точно кратных LSB. А для реального преобразователя такое условие может выполняться с погрешностью. Разность между «идеальными» уровнями напряжения, при которых происходит кодовый переход, и их реальными значениями выражается в единицах LSB и называется интегральной нелинейностью.
Одна из наиболее существенных составляющих ошибки при измерениях с помощью АЦП — погрешность квантования -является результатом самого процесса преобразования. Погрешность квантования — это погрешность, вызванная значением шага квантования и определяемая как ½ величины наименьшего значащего разряда (LSB). Она не может быть исключена в аналого-цифровых преобразованиях, так как является неотъемлемой частью процесса преобразования, определяется разрешающей способностью АЦП и не меняется от АЦП к АЦП с равным разрешением.
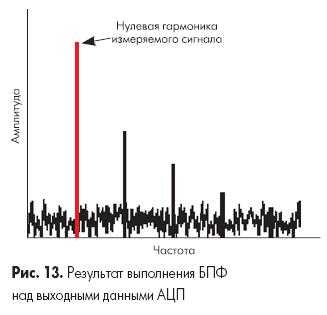
Динамические характеристики АЦП обычно определяют с помощью спектрального анализа, по результатам выполнения быстрого преобразования Фурье (БПФ) над массивом выходных значений АЦП, соответствующих некоторому тестовому входному сигналу.
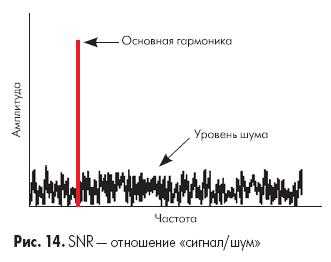
На рис. 13 представлен пример частотного спектра измеряемого сигнала. Нулевая гармоника соответствует основной частоте входного сигнала. Все остальное представляет собой шум, который содержит гармонические искажения, тепловой шум, шум 1/f и шум квантования. Некоторые составляющие шума генерируются самим АЦП, некоторые могут поступать на вход АЦП из внешних цепей. Гармонические искажения, например, могут содержаться в измеряемом сигнале и одновременно генерироваться АЦП в процессе преобразования.
Отношение «сигнал/шум» (SNR) — это отношение среднеквадратического значения величины входного сигнала к среднеквадратическому значению величины шума (за исключением гармонических искажений), выраженное в децибелах:
SNR(dB) = 20 log [ Vsignal(rms)/ Vnoise(rms) ]
Это значение позволяет определить долю шума в измеряемом сигнале по отношению к полезному сигналу.
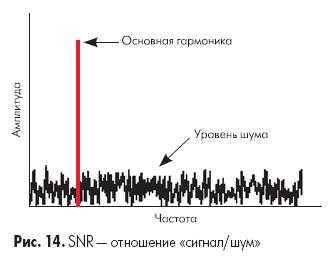
Шум, измеряемый при расчете SNR, не включает гармонические искажения, но включает шум квантования. Для АЦП с определенным разрешением именно шум квантования ограничивает возможности преобразователя теоретически лучшим значением отношения сигнал/шум, которое определяется как:
SNR(db) = 6.02 N + 1.76,
где N — разрешение АЦП.
Спектр шума квантования АЦП стандартных архитектур имеет равномерное распределение по частоте. Поэтому величина этого шума не может быть уменьшена путем увеличения времени преобразования и последующего усреднения результатов. Шум квантования может быть снижен только путем проведения измерений с помощью АЦП большей разрядности.
Особенность сигма-дельта АЦП состоит в том, что спектр шума квантования у него распределен по частоте неравномерно — он смещен в сторону высоких частот. Поэтому, увеличивая время измерения (и, соответственно, количество выборок измеряемого сигнала), накапливая и затем усредняя полученную выборку (фильтр нижних частот), можно получить результат измерений с более высокой точностью. Естественно, при этом общее время преобразования будет возрастать.
Другие источника шума АЦП включают тепловой шум, шум составляющей 1/f и джиттер опорной частоты.
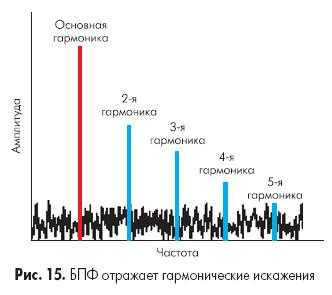
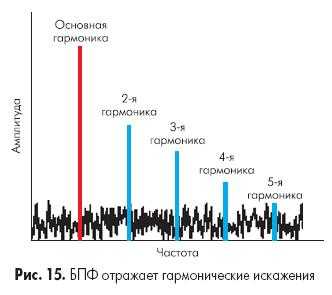
Нелинейность в результатах преобразования данных приводит к появлению гармонических искажений. Такие искажения наблюдаются как «выбросы» в спектре частот на четных и нечетных гармониках измеряемого сигнала (рис. 15).
Эти искажения определяют как общие гармонические искажения (THD). Они определяются как:
Величина гармонических искажений уменьшается на высоких частотах до точки, в которой амплитуда гармоник становится меньше, чем уровень шума. Таким образом, если мы анализируем вклад гармонических искажений в результаты преобразования, это можно делать либо во всем спектре частот, ограничивая при этом амплитуду гармоник уровнем шума, либо ограничивая полосу частот для анализа. Например, если в нашей системе стоит ФНЧ, то высокие частоты нам просто неинтересны и высокочастотные гармоники не подлежат учету.
Отношение «сигнал/шум и искажения» (SiNAD) более полно описывает шумовые характеристики АЦП. SiNAD учитывает величину как шума, так и гармонических искажений по отношению к полезному сигналу. SiNAD рассчитывается по следующей формуле:
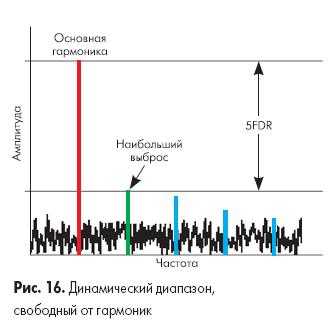
Динамический диапазон, свободный от гармоник, представляет собой разницу между величиной измеряемого сигнала и наибольшим пиком искажений (см. рис.16). Этот динамический диапазон обозначается как SFDR. Он ограничен снизу амплитудой максимальной гармоники паразитных выбросов на выходе АЦП в диапазоне его рабочих частот.
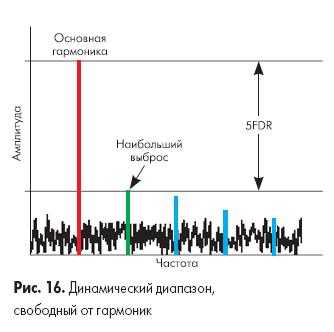
Спецификация АЦП, приводимая в технической документации на микросхемы, помогает обоснованно выбрать преобразователь для конкретного применения. В качестве примера рассмотрим спецификацию АЦП, интегрированного в новый микроконтроллер C8051F064 производства фирмы Silicon Laboratories.
Кристалл C8051F064 представляет собой скоростной 8-разрядный микроконтроллер для совместной обработки аналоговых и цифровых сигналов с двумя интегрированными 16-разрядными АЦП последовательных приближений. Встроенные АЦП могут работать в однопроводном и дифференциальном режимах при максимальной производительности до 1М отсчетов/сек. На рис. 17 приведены основные характеристики АЦП микроконтроллера C8051F064. Для самостоятельной оценки возможностей C8051F064 по цифровой и аналоговой обработке данных можно воспользоваться недорогим оценочным комплектом C8051F064EK (рис. 18). Комплект содержит оценочную плату на базе C8051F064, USB-кабель, документацию, а также программное обеспечение для тестирования аналоговых динамических и статических характеристик интегрированного высокоточного 16-разрядного АЦП.
| Параметры | Условия | Мин. | Типичное | Макс. | Единицы измерения |
| Характеристики на постоянном токе | |||||
| Разрядность | 16 | бит | |||
| Интегральная нелинейность | Однопроводный | ±0.75 | ±2 | LSB | |
| Однопроводный | ±0.5 | ±1 | LSB | ||
| Дифференциальная нелинейность | Гарантированная монотонность | ±+0.5 | LSB | ||
| Аддитивная погрешность (смещение) | 0.1 | мВ | |||
| Мультипликативная погрешность | 0.008 | % F.S. | |||
| Температурный коэффициент усиления | 0.5 | ppm/°C | |||
| Динамические характеристики (Частота дискретизации 1 Msps, AVDD, AV+ = 3.3 В) | |||||
| Сигнал/шум и искажения | Fin = 10 кГц, однопроводный | 86 | дБ | ||
| Fin = 100 кГц, однопроводный | 84 | дБ | |||
| Fin = 10 кГц, дифференциальный | 89 | дБ | |||
| Fin = 100 кГц, дифференциальный | 88 | дБ | |||
| Общие гармонические искажения | Fin = 10 кГц, однопроводный | 96 | дБ | ||
| Fin = 100 кГц, однопроводный | 84 | дБ | |||
| Fin = 10 кГц, дифференциальный | 103 | дБ | |||
| Fin = 100 кГц, дифференциальный | 93 | дБ | |||
| Динамический диапазон, свободный от гармоник | Fin = 10 кГц, однопроводный | 97 | дБ | ||
| Fin = 100 кГц, однопроводный | 88 | дБ | |||
| Fin = 10 кГц, дифференциальный | 104 | дБ | |||
| Fin = 100 кГц, дифференциальный | 99 | дБ | |||
Cписок литературы.
lab201.jimdo.com
Вольфганг Райс (Wolfgang Reis, WBC GmbH)
Журнал «Компоненты и технологии», № 3’2005
В статье рассказывается об устройстве и принципах действия аналогово-цифровых преобразователей различных типов, а также об их основных характеристиках, указываемых производителями в документации.
Аналогово-цифровой преобразователь (АЦП) — один из самых важных электронных компонентов в измерительном и тестовом оборудовании. АЦП преобразует напряжение (аналоговый сигнал) в код, над которым микропроцессор и программное обеспечение выполняют определенные действия. Даже если Вы работаете только с цифровыми сигналами, скорее всего Вы используете АЦП в составе осциллографа, чтобы узнать их аналоговые характеристики.
Существует несколько основных типов архитектуры АЦП, хотя в пределах каждого типа существует также множество вариаций. Различные типы измерительного оборудования используют различные типы АЦП. Например, в цифровом осциллографе используется высокая частота дискретизации, но не требуется высокое разрешение. В цифровых мультиметрах нужно большее разрешение, но можно пожертвовать скоростью измерения. Системы сбора данных общего назначения по скорости дискретизации и разрешающей способности обычно занимают место между осциллографами и цифровыми мультиметрами. В оборудовании такого типа используются АЦП последовательного приближения либо сигма-дельта АЦП. Существуют также параллельные АЦП для приложений, требующих скоростной обработки аналоговых сигналов, и интегрирующие АЦП с высокими разрешением и помехоподавлением.
На рис.1. показаны возможности основных архитектур АЦП в зависимости от разрешения и частоты дискретизации.
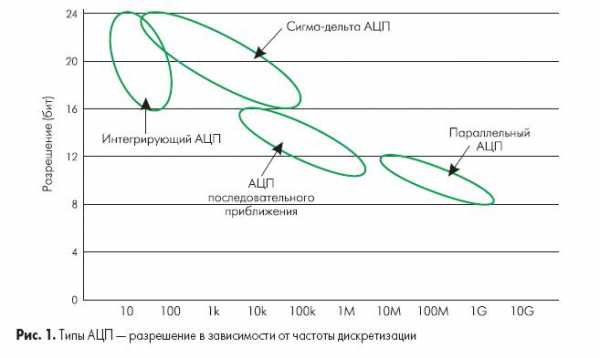
Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5Г (5*109) отсчетов/сек для стандартных устройств и 20Г отсчетов/сек для оригинальных разработок. Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10-ти разрядные версии.
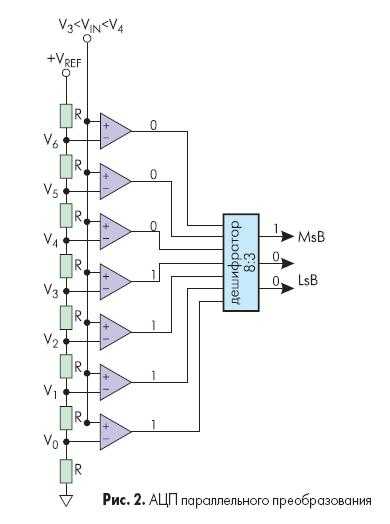
Рис. 2 показывает упрощенную блок-схему 3-х разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется). Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным VREF /23. В результате для 3-х разрядного АЦП требуется 23-1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (28-1)) компараторов.
С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рис. 2 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе «1», а верхние три компаратора — «0». Дешифратор преобразует (23-1) — разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код.
Параллельные АЦП — достаточно быстрые устройства, но они имеют свои недостатки. Из-за необходимости использовать большое количество компараторов параллельные АЦП потребляют значительную мощность, и их нецелесообразно использовать в приложениях с батарейным питанием.
Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 100К (1х103) до 1М (1х106) отсчетов/сек.
Рис. 3 показывает упрощенную блок-схему АЦП последовательного приближения. В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0, за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением.
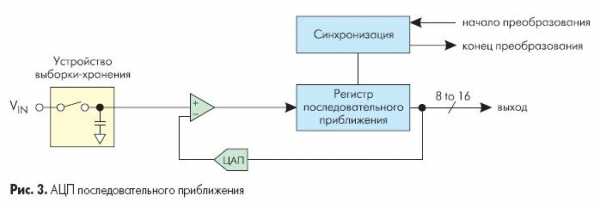
Например, для 8-разрядного АЦП последовательного приближения (рис. 4) выходы регистра при этом устанавливаются в «10000000». Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0. Это дает регистру последовательного приближения команду переключить свои выходы в состояние «01000000», что соответственно приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в «0», то выходы регистра переключились бы в состояние «00100000». Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение (рис. 4), и компаратор переключается в состояние логической 1. Это предписывает регистру последовательного приближения сохранить «1» во втором разряде и подать «1» на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования.
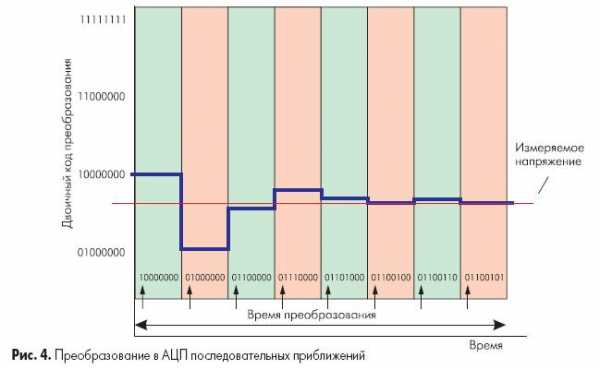
Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП. Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа.
Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100К отсчетов/сек, а при 24 разрядах эта частота падает до 1К отсчетов/сек и менее, в зависимости от устройства.
Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов.
Принцип работы сигма-дельта АЦП сложнее для понимания. Эта архитектура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8М отсчетов/сек.
Блок-схема сигма-дельта АЦП первого порядка приведена на рис. 5. Аналоговый сигнал подается на интегратор, выходы которого подсоединены к компаратору, который в свою очередь присоединен к 1-разрядному ЦАП в петле обратной связи. Путем серии последовательных итераций интегратор, компаратор, ЦАП и сумматор дают поток последовательных битов, в котором содержится информация о величине входного напряжения.
Результирующая цифровая последовательность затем подается на фильтр нижних частот для подавления компонентов с частотами выше частоты Котельникова (она составляет половину частоты дискретизации АЦП). После удаления высокочастотных составляющих следующий узел — дециматор — прореживает данные. В рассматриваемом нами АЦП дециматор будет оставлять 1 бит из каждых полученных 128 в выходной цифровой последовательности.
Так как внутренний цифровой ФНЧ в сигма-дельта АЦП представляет собой неотъемлемую часть для осуществления процесса преобразования, время установления ФНЧ становится фактором, который необходимо учитывать при скачкообразном изменении входного сигнала. Например, при переключении входного мультиплексора или при переключении предела измерения прибора необходимо подождать, пока пройдут несколько отсчетов АЦП, и лишь потом считывать корректные выходные данные.
Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП.
И последний тип АЦП, о котором пойдет здесь речь — АЦП двухтактного интегрирования. В цифровых мультиметрах, как правило, используются именно такие АЦП, т.к. в этих измерительных приборах необходимо сочетание высокого разрешения и высокого помехоподавления. Идея преобразования в таком интегрирующем АЦП гораздо менее сложна, чем в сигма-дельта АЦП.
На рисунке 6 показан принцип работы АЦП двухтактного интегрирования. Входной сигнал заряжает конденсатор в течение фиксированного периода времени, который обычно составляет один период частоты питающей сети (50 или 60Гц) или кратен ему. При интегрировании входного сигнала в течение промежутка времени такой длительности высокочастотные помехи подавляются. Одновременно исключается влияние нестабильности напряжения сетевого источника питания на точность преобразования. Это происходит потому, что значение интеграла от синусоидального сигнала равно нулю, если интегрирование осуществляется во временном интервале, кратном периоду изменения синусоиды.
По окончании времени заряда АЦП разряжает конденсатор с фиксированной скоростью, в то время как внутренний счетчик подсчитывает количество тактовых импульсов за время разряда конденсатора. Большее время разряда, таким образом, соответствует большему значению показаний счетчика и большему измеряемому напряжению (рис.6).
АЦП двухтактного интегрирования имеют высокую точность и высокую разрешающую способность, а также имеют сравнительно простую структуру. Это дает возможность выполнять их в виде интегральных микросхем. Основной недостаток таких АЦП — большое время преобразования, обусловленное привязкой периода интегрирования к длительности периода питающей сети. Например, для 50 Гц — оборудования частота дискретизации АЦП двухтактного интегрирования не превышает 25 отсчетов/сек. Конечно, такие АЦП могут работать и с большей частотой дискретизации, но при увеличении последней помехозащищенность падает.
Существуют общие определения, которые принято использовать в отношении аналого-цифровых преобразователей. Тем не менее, характеристики, приводимые в технической документации производителей АЦП, могут показаться довольно путаными. Правильный же выбор оптимального по сочетанию своих характеристик АЦП для конкретного приложения требует точной интерпретации данных, приводимых в технической документации.
Наиболее часто путаемыми параметрами являются разрешающая способность и точность, хотя эти две характеристики реального АЦП крайне слабо связаны между собой. Разрешение не идентично точности, 12-разрядный АЦП может иметь меньшую точность, чем 8-разрядный. Для АЦП разрешение представляет собой меру того, на какое количество сегментов может быть поделен входной диапазон измеряемого аналогового сигнала (например, для 8-разрядного АЦП это 28=256 сегментов). Точность же характеризует суммарное отклонение результата преобразования от своего идеального значения для данного входного напряжения. То есть, разрешающая способность характеризует потенциальные возможности АЦП, а совокупность точностных параметров определяет реализуемость такой потенциальной возможности.
АЦП преобразует входной аналоговый сигнал в выходной цифровой код. Для реальных преобразователей, изготавливаемых в виде интегральных микросхем, процесс преобразования не является идеальным: на него оказывают влияние как технологический разброс параметров при производстве, так и различные внешние помехи. Поэтому цифровой код на выходе АЦП определяется с погрешностью. В спецификации на АЦП указываются погрешности, которые дает сам преобразователь. Их обычно делят на статические и динамические. При этом именно конечное приложение определяет, какие характеристики АЦП будут считаться определяющими, самыми важными в каждом конкретном случае.
В большинстве применений АЦП используют для измерения медленно изменяющегося, низкочастотного сигнала (например, от датчика температуры, давления, от тензодатчика и т.п.), когда входное напряжение пропорционально относительно постоянной физической величине. Здесь основную роль играет статическая погрешность измерения. В спецификации АЦП этот тип погрешности определяют аддитивная погрешность (Offset), мультипликативная погрешность (Full-Scale), дифференциальная нелинейность (DNL), интегральная нелинейность (INL) и погрешность квантования. Эти пять характеристик позволяют полностью описать статическую погрешность АЦП.
Передаточная характеристика АЦП — это функция зависимости кода на выходе АЦП от напряжения на его входе. Такой график представляет собой кусочно-линейную функцию из 2N «ступеней», где N — разрядность АЦП. Каждый горизонтальный отрезок этой функции соответствует одному из значений выходного кода АЦП (см. рис. 7). Если соединить линиями начала этих горизонтальных отрезков (на границах перехода от одного значения кода к другому), то идеальная передаточная характеристика будет представлять собой прямую линию, проходящую через начало координат.
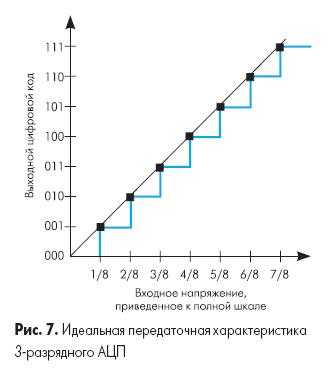
Рис. 7 иллюстрирует идеальную передаточную характеристику для 3-х разрядного АЦП с контрольными точками на границах перехода кода. Выходной код принимает наименьшее значение (000b) при значении входного сигнала от 0 до 1/8 полной шкалы (максимального значения кода этого АЦП). Также следует отметить, что АЦП достигнет значения кода полной шкалы (111b) при 7/8 полной шкалы, а не при значении полной шкалы. Т.о. переход в максимальное значение на выходе происходит не при напряжении полной шкалы, а при значении, меньшем на наименьший значащий разряд (LSB), чем входное напряжение полной шкалы. Передаточная характеристика может быть реализована со смещением -1/2 LSB. Это достигается смещением передаточной характеристики влево, что смещает погрешность квантования из диапазона -1… 0 LSB в диапазон -1/2 … +1/2 LSB.
Из-за технологического разброса параметров при изготовлении интегральных микросхем реальные АЦП не имеют идеальной передаточной характеристики. Отклонения от идеальной передаточной характеристики определяют статическую погрешность АЦП и приводятся в технической документации.
Идеальная передаточная характеристика АЦП пересекает начало координат, а первый переход кода происходит при достижении значения 1 LSB. Аддитивная погрешность (погрешность смещения) может быть определена как смещение всей передаточной характеристики влево или вправо относительно оси входного напряжения, как показано на рис.9. Таким образом, в определение аддитивной погрешности АЦП намеренно включено смещение 1/2 LSB.
Мультипликативная погрешность (погрешность полной шкалы) представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии нулевой аддитивной погрешности (смещение отсутствует). Это проявляется как изменение наклона передаточной функции, что иллюстрирует рис. 10.
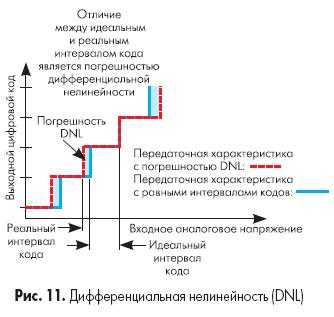
Дифференциальная нелинейность
У идеальной передаточной характеристики АЦП ширина каждой «ступеньки» должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из 2N «ступеней» представляет собой дифференциальную нелинейность (DNL).
Величина наименьшего значащего разряда у АЦП составляет Vref/2N, где Vref — опорное напряжение, N — разрешение АЦП. Разность напряжений между каждым кодовым переходом должна быть равна величине LSB. Отклонение этой разности от LSB определяются как дифференциальная нелинейность. На рисунке это показано как неравные промежутки между «шагами» кода или как «размытость» границ переходов на передаточной характеристике АЦП.
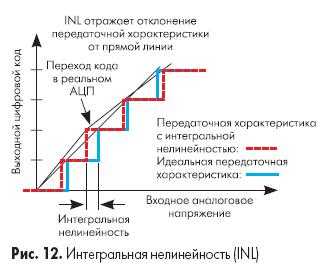
Интегральная нелинейность (INL) — это погрешность, которая вызывается отклонением линейной функции передаточной характеристики АЦП от прямой линии, как показано на рис. 12. Обычно передаточная функция с интегральной нелинейностью аппроксимируется прямой линией по методу наименьших квадратов. Часто аппроксимирующей прямой просто соединяют наименьшее и наибольшее значения. Интегральную нелинейность определяют путем сравнения напряжений, при которых происходят кодовые переходы. Для идеального АЦП эти переходы будут происходить при значениях входного напряжения, точно кратных LSB. А для реального преобразователя такое условие может выполняться с погрешностью. Разность между «идеальными» уровнями напряжения, при которых происходит кодовый переход, и их реальными значениями выражается в единицах LSB и называется интегральной нелинейностью.
Одна из наиболее существенных составляющих ошибки при измерениях с помощью АЦП — погрешность квантования -является результатом самого процесса преобразования. Погрешность квантования — это погрешность, вызванная значением шага квантования и определяемая как ½ величины наименьшего значащего разряда (LSB). Она не может быть исключена в аналого-цифровых преобразованиях, так как является неотъемлемой частью процесса преобразования, определяется разрешающей способностью АЦП и не меняется от АЦП к АЦП с равным разрешением.
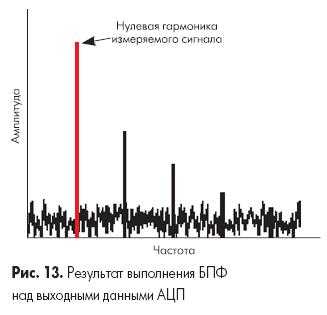
Динамические характеристики АЦП обычно определяют с помощью спектрального анализа, по результатам выполнения быстрого преобразования Фурье (БПФ) над массивом выходных значений АЦП, соответствующих некоторому тестовому входному сигналу.
На рис. 13 представлен пример частотного спектра измеряемого сигнала. Нулевая гармоника соответствует основной частоте входного сигнала. Все остальное представляет собой шум, который содержит гармонические искажения, тепловой шум, шум 1/f и шум квантования. Некоторые составляющие шума генерируются самим АЦП, некоторые могут поступать на вход АЦП из внешних цепей. Гармонические искажения, например, могут содержаться в измеряемом сигнале и одновременно генерироваться АЦП в процессе преобразования.
Отношение «сигнал/шум» (SNR) — это отношение среднеквадратического значения величины входного сигнала к среднеквадратическому значению величины шума (за исключением гармонических искажений), выраженное в децибелах:
SNR(dB) = 20 log [ Vsignal(rms)/ Vnoise(rms) ]
Это значение позволяет определить долю шума в измеряемом сигнале по отношению к полезному сигналу.
Шум, измеряемый при расчете SNR, не включает гармонические искажения, но включает шум квантования. Для АЦП с определенным разрешением именно шум квантования ограничивает возможности преобразователя теоретически лучшим значением отношения сигнал/шум, которое определяется как:
SNR(db) = 6.02 N + 1.76,
где N — разрешение АЦП.
Спектр шума квантования АЦП стандартных архитектур имеет равномерное распределение по частоте. Поэтому величина этого шума не может быть уменьшена путем увеличения времени преобразования и последующего усреднения результатов. Шум квантования может быть снижен только путем проведения измерений с помощью АЦП большей разрядности.
Особенность сигма-дельта АЦП состоит в том, что спектр шума квантования у него распределен по частоте неравномерно — он смещен в сторону высоких частот. Поэтому, увеличивая время измерения (и, соответственно, количество выборок измеряемого сигнала), накапливая и затем усредняя полученную выборку (фильтр нижних частот), можно получить результат измерений с более высокой точностью. Естественно, при этом общее время преобразования будет возрастать.
Другие источника шума АЦП включают тепловой шум, шум составляющей 1/f и джиттер опорной частоты.
Нелинейность в результатах преобразования данных приводит к появлению гармонических искажений. Такие искажения наблюдаются как «выбросы» в спектре частот на четных и нечетных гармониках измеряемого сигнала (рис. 15).
Эти искажения определяют как общие гармонические искажения (THD). Они определяются как:
Величина гармонических искажений уменьшается на высоких частотах до точки, в которой амплитуда гармоник становится меньше, чем уровень шума. Таким образом, если мы анализируем вклад гармонических искажений в результаты преобразования, это можно делать либо во всем спектре частот, ограничивая при этом амплитуду гармоник уровнем шума, либо ограничивая полосу частот для анализа. Например, если в нашей системе стоит ФНЧ, то высокие частоты нам просто неинтересны и высокочастотные гармоники не подлежат учету.
Отношение «сигнал/шум и искажения» (SiNAD) более полно описывает шумовые характеристики АЦП. SiNAD учитывает величину как шума, так и гармонических искажений по отношению к полезному сигналу. SiNAD рассчитывается по следующей формуле:
Динамический диапазон, свободный от гармоник, представляет собой разницу между величиной измеряемого сигнала и наибольшим пиком искажений (см. рис.16). Этот динамический диапазон обозначается как SFDR. Он ограничен снизу амплитудой максимальной гармоники паразитных выбросов на выходе АЦП в диапазоне его рабочих частот.
Спецификация АЦП, приводимая в технической документации на микросхемы, помогает обоснованно выбрать преобразователь для конкретного применения. В качестве примера рассмотрим спецификацию АЦП, интегрированного в новый микроконтроллер C8051F064 производства фирмы Silicon Laboratories.
Кристалл C8051F064 представляет собой скоростной 8-разрядный микроконтроллер для совместной обработки аналоговых и цифровых сигналов с двумя интегрированными 16-разрядными АЦП последовательных приближений. Встроенные АЦП могут работать в однопроводном и дифференциальном режимах при максимальной производительности до 1М отсчетов/сек. На рис. 17 приведены основные характеристики АЦП микроконтроллера C8051F064. Для самостоятельной оценки возможностей C8051F064 по цифровой и аналоговой обработке данных можно воспользоваться недорогим оценочным комплектом C8051F064EK (рис. 18). Комплект содержит оценочную плату на базе C8051F064, USB-кабель, документацию, а также программное обеспечение для тестирования аналоговых динамических и статических характеристик интегрированного высокоточного 16-разрядного АЦП.
| Параметры | Условия | Мин. | Типичное | Макс. | Единицы измерения |
| Характеристики на постоянном токе | |||||
| Разрядность | 16 | бит | |||
| Интегральная нелинейность | Однопроводный | ±0.75 | ±2 | LSB | |
| Однопроводный | ±0.5 | ±1 | LSB | ||
| Дифференциальная нелинейность | Гарантированная монотонность | ±+0.5 | LSB | ||
| Аддитивная погрешность (смещение) | 0.1 | мВ | |||
| Мультипликативная погрешность | 0.008 | % F.S. | |||
| Температурный коэффициент усиления | 0.5 | ppm/°C | |||
| Динамические характеристики (Частота дискретизации 1 Msps, AVDD, AV+ = 3.3 В) | |||||
| Сигнал/шум и искажения | Fin = 10 кГц, однопроводный | 86 | дБ | ||
| Fin = 100 кГц, однопроводный | 84 | дБ | |||
| Fin = 10 кГц, дифференциальный | 89 | дБ | |||
| Fin = 100 кГц, дифференциальный | 88 | дБ | |||
| Общие гармонические искажения | Fin = 10 кГц, однопроводный | 96 | дБ | ||
| Fin = 100 кГц, однопроводный | 84 | дБ | |||
| Fin = 10 кГц, дифференциальный | 103 | дБ | |||
| Fin = 100 кГц, дифференциальный | 93 | дБ | |||
| Динамический диапазон, свободный от гармоник | Fin = 10 кГц, однопроводный | 97 | дБ | ||
| Fin = 100 кГц, однопроводный | 88 | дБ | |||
| Fin = 10 кГц, дифференциальный | 104 | дБ | |||
| Fin = 100 кГц, дифференциальный | 99 | дБ | |||
Cписок литературы.
mymcu.ru
Аналого-цифровой преобразователь[1][2][3] (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал). Обратное преобразование осуществляется при помощи ЦАП (цифро-аналогового преобразователя, DAC).
Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.
Итальянский математик Фибоначчи сформулировал задачу наименьшего числа гирь целочисленного веса для взвешивания грузов наибольшего диапазона на рычажных весах, которая стала известна под названием задача о гирях[4] (задача Баше — Менделеева). Фибоначчи пришёл к выводу, что, при взвешивании с разрешением класть гири только на одну чашу весов, наименьшее число гирь получается при выборе весов гирь из ряда 1, 2, 4, 8, 16,… (степени 2), что соответствует весам разрядов в двоичной системе счисления, при взвешивании с разрешением класть гири на обе чаши весов, наименьшее число гирь получается при выборе весов гирь из ряда 1, 3, 9, 27, 81,… (степени 3, последовательность A000244 в OEIS) что соответствует весам разрядов в троичных системах счисления[5].
Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП — связано с его разрядностью. В случае единичного измерения без учёта шумов разрешение напрямую определяется разрядностью АЦП.
Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП измеряется в битах, в троичных АЦП измеряется в тритах. Например, двоичный 8-ми разрядный АЦП, способен выдать 256 дискретных значений (0…255), поскольку , троичный 8-ми разрядный АЦП, способен выдать 6561 дискретное значение, поскольку .
Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений. Например:
На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (effective number of bits, ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. Для достижения заявленной разрядности отношение С/Ш входного сигнала должно быть примерно 6 дБ на каждый бит разрядности (6 дБ соответствует двукратному изменению уровня сигнала).
По способу применяемых алгоритмов АЦП делят на:
Передаточная характеристика АЦП — зависимость числового эквивалента выходного двоичного кода от величины входного аналогового сигнала. Говорят о линейных и нелинейных АЦП. Такое деление условное. Обе передаточные характеристики — ступенчатые. Но для «линейных» АЦП всегда возможно провести такую прямую линию, чтобы все точки передаточной характеристики, соответствующие входным значениям delta*2^k (где delta — шаг дискретизации, k лежит в диапазоне 0..N, где N — разрядность АЦП) были от неё равноудалены.
Большинство АЦП считаются линейными, хотя аналого-цифровое преобразование по сути является нелинейным процессом (поскольку операция отображения непрерывного пространства в дискретное — операция нелинейная).
Термин линейный применительно к АЦП означает, что диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением, то есть выходное значение k достигается при диапазоне входных значений от
до
где m и b — некоторые константы. Константа b, как правило, имеет значение 0 или −0.5. Если b = 0, АЦП называют квантователь с ненулевой ступенью (mid-rise), если же b = −0,5, то АЦП называют квантователь с нулём в центре шага квантования (mid-tread).
Если бы плотность вероятности амплитуды входного сигнала имела равномерное распределение, то отношение сигнал/шум (применительно к шуму квантования) было бы максимально возможным. По этой причине обычно перед квантованием по амплитуде сигнал пропускают через безынерционный преобразователь, передаточная функция которого повторяет функцию распределения самого сигнала. Это улучшает достоверность передачи сигнала, так как наиболее важные области амплитуды сигнала квантуются с лучшим разрешением. Соответственно, при цифро-аналоговом преобразовании потребуется обработать сигнал функцией, обратной функции распределения исходного сигнала.
Это тот же принцип, что и используемый в компандерах, применяемых в магнитофонах и различных коммуникационных системах, он направлен на максимизацию энтропии. (Не путать компандер с компрессором!)
Например, голосовой сигнал имеет лапласово распределение амплитуды. Это означает, что окрестность нуля по амплитуде несёт больше информации, чем области с большей амплитудой. По этой причине логарифмические АЦП часто применяются в системах передачи голоса для увеличения динамического диапазона передаваемых значений без изменения качества передачи сигнала в области малых амплитуд.
8-битные логарифмические АЦП с a-законом или μ-законом обеспечивают широкий динамический диапазон и имеют высокое разрешение в наиболее критичном диапазоне малых амплитуд; линейный АЦП с подобным качеством передачи должен был бы иметь разрядность около 12 бит.
Имеется несколько источников погрешности АЦП. Ошибки квантования и (считая, что АЦП должен быть линейным) нелинейности присущи любому аналого-цифровому преобразованию. Кроме того, существуют так называемые апертурные ошибки которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта).
Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд. В приведённом выше примере 8-битного двоичного АЦП ошибка в 1 МЗР составляет 1/256 от полного диапазона сигнала, то есть 0,4 %, в 5-тритном троичном АЦП ошибка в 1 МЗР составляет 1/243 от полного диапазона сигнала, то есть 0,412 %, в 8-тритном троичном АЦП ошибка в 1 МЗР составляет 1/6561, то есть 0,015 %.
Ошибки квантования являются следствием ограниченного разрешения АЦП. Этот недостаток не может быть устранён ни при каком типе аналого-цифрового преобразования. Абсолютная величина ошибки квантования при каждом отсчёте находится в пределах от нуля до половины МЗР.
Как правило, амплитуда входного сигнала много больше, чем МЗР. В этом случае ошибка квантования не коррелирована с сигналом и имеет равномерное распределение. Её среднеквадратическое значение совпадает с среднеквадратичным отклонением распределения, которое равно . В случае 8-битного АЦП это составит 0,113 % от полного диапазона сигнала.
Всем АЦП присущи ошибки, связанные с нелинейностью, которые являются следствием физического несовершенства АЦП. Это приводит к тому, что передаточная характеристика (в указанном выше смысле) отличается от линейной (точнее от желаемой функции, так как она не обязательно линейна). Ошибки могут быть уменьшены путём калибровки.
Важным параметром, описывающим нелинейность, является интегральная нелинейность (INL) и дифференциальная нелинейность (DNL).
Пусть мы оцифровываем синусоидальный сигнал . В идеальном случае отсчёты берутся через равные промежутки времени. Однако в реальности время момента взятия отсчёта подвержено флуктуациям из-за дрожания фронта синхросигнала (clock jitter). Полагая, что неопределённость момента времени взятия отсчёта порядка , получаем, что ошибка, обусловленная этим явлением, может быть оценена как
Легко видеть, что ошибка относительно невелика на низких частотах, однако на больших частотах она может существенно возрасти.
Эффект апертурной погрешности может быть проигнорирован, если её величина сравнительно невелика по сравнению с ошибкой квантования. Таким образом, можно установить следующие требования к дрожанию фронта сигнала синхронизации:
где — разрядность АЦП.
| Разрядность АЦП | Максимальная частота входного сигнала | ||||
|---|---|---|---|---|---|
| 44,1 кГц | 192 кГц | 1 МГц | 10 МГц | 100 МГц | |
| 8 | 28,2 нс | 6,48 нс | 1,24 нс | 124 пс | 12,4 пс |
| 10 | 7,05 нс | 1,62 нс | 311 пс | 31,1 пс | 3,11 пс |
| 12 | 1,76 нс | 405 пс | 77,7 пс | 7,77 пс | 777 фс |
| 14 | 441 пс | 101 пс | 19,4 пс | 1,94 пс | 194 фс |
| 16 | 110 пс | 25,3 пс | 4,86 пс | 486 фс | 48,6 фс |
| 18 | 27,5 пс | 6,32 пс | 1,21 пс | 121 фс | 12,1 фс |
| 24 | 430 фс | 98,8 фс | 19,0 фс | 1,9 фс | 190 ас |
Из этой таблицы можно сделать вывод о целесообразности применения АЦП определённой разрядности с учётом ограничений, накладываемых дрожанием фронта синхронизации (clock jitter). Например, бессмысленно использовать прецизионный 24-битный АЦП для записи звука, если система распределения синхросигнала не в состоянии обеспечить ультрамалой неопределённости.
Вообще, качество тактового сигнала чрезвычайно важно не только по этой причине. Например, из описания микросхемы AD9218 (Analog Devices):
Any high speed ADC is extremely sensitive to the quality of the sampling clock provided by the user. A track-and-hold circuit is essentially a mixer. Any noise, distortion, or timing jitter on the clock is combined with the desired signal at the analog-to-digital output.
То есть, любой высокоскоростной АЦП крайне чувствителен к качеству оцифровывающей тактовой частоты, подаваемой пользователем. Схема выборки и хранения, по сути, является смесителем (перемножителем). Любой шум, искажения, или дрожание фазы тактовой частоты смешиваются с полезным сигналом и поступают на цифровой выход.
Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала. Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП.
Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации) и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции. Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова — Шеннона точное восстановление возможно только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала.
Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным по крайней мере от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения (УВХ). УВХ, как правило, хранит входное напряжение на конденсаторе, который соединён со входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение. Многие АЦП, выполненные в виде интегральных микросхем содержат встроенное УВХ.
Все АЦП работают путём выборки входных значений через фиксированные интервалы времени. Следовательно, выходные значения являются неполной картиной того, что подаётся на вход. Глядя на выходные значения, нет никакой возможности установить, как вёл себя входной сигнал между выборками. Если известно, что входной сигнал меняется достаточно медленно относительно частоты дискретизации, то можно предположить, что промежуточные значения между выборками находятся где-то между значениями этих выборок. Если же входной сигнал меняется быстро, то никаких предположений о промежуточных значениях входного сигнала сделать нельзя, а следовательно, невозможно однозначно восстановить форму исходного сигнала.
Если последовательность цифровых значений, выдаваемая АЦП, где-либо преобразуется обратно в аналоговую форму цифро-аналоговым преобразователем, желательно, чтобы полученный аналоговый сигнал был максимально точной копией исходного сигнала. Если входной сигнал меняется быстрее, чем делаются его отсчёты, то точное восстановление сигнала невозможно, и на выходе ЦАП будет присутствовать ложный сигнал. Ложные частотные компоненты сигнала (отсутствующие в спектре исходного сигнала) получили название alias (ложная частота, побочная низкочастотная составляющая). Частота ложных компонент зависит от разницы между частотой сигнала и частотой дискретизации. Например, синусоидальный сигнал с частотой 2 кГц, дискретизованный с частотой 1.5 кГц был бы воспроизведён как синусоида с частотой 500 Гц. Эта проблема получила название наложение частот (aliasing).
Для предотвращения наложения спектров сигнал, подаваемый на вход АЦП, должен быть пропущен через фильтр нижних частот для подавления спектральных компонент, частота которых превышает половину частоты дискретизации. Этот фильтр получил название anti-aliasing (антиалиасинговый) фильтр, его применение чрезвычайно важно при построении реальных АЦП.
Вообще, применение аналогового входного фильтра интересно не только по этой причине. Казалось бы, цифровой фильтр, который обычно применяется после оцифровки, имеет несравненно лучшие параметры. Но, если в сигнале присутствуют компоненты, значительно более мощные, чем полезный сигнал, и достаточно далеко отстоящие от него по частоте, чтобы быть эффективно подавленными аналоговым фильтром, такое решение позволяет сохранить динамический диапазон АЦП: если помеха на 10 дБ сильнее сигнала, на неё впустую будет тратиться, в среднем, три бита разрядности.
Хотя наложение спектров в большинстве случаев является нежелательным эффектом, его можно использовать во благо. Например, благодаря этому эффекту можно обойтись без преобразования частоты вниз при оцифровке узкополосного высокочастотного сигнала (смотри смеситель). Для этого, однако, входные аналоговые каскады АЦП должны иметь значительно более высокие параметры, чем это требуется для стандартного использования АЦП на основной (видео или низшей) гармонике. Также для этого необходимо обеспечить эффективную фильтрацию внеполосных частот до АЦП, так как после оцифровки, нет никакой возможности идентифицировать и/или отфильтровать большинство из них.
Некоторые характеристики АЦП могут быть улучшены путём использования методики подмешивания псевдослучайного сигнала (англ. dither). Она заключается в добавлении к входному аналоговому сигналу случайного шума (белый шум) небольшой амплитуды. Амплитуда шума, как правило, выбирается на уровне половины МЗР. Эффект от такого добавления заключается в том, что состояние МЗР случайным образом переходит между состояниями 0 и 1 при очень малом входном сигнале (без добавления шума МЗР был бы в состоянии 0 или 1 долговременно). Для сигнала с подмешанным шумом вместо простого округления сигнала до ближайшего разряда происходит случайное округление вверх или вниз, причём среднее время, в течение которого сигнал округлён к тому или иному уровню зависит от того, насколько сигнал близок к этому уровню. Таким образом, оцифрованный сигнал содержит информацию об амплитуде сигнала с разрешающей способностью лучше, чем МЗР, то есть происходит увеличение эффективной разрядности АЦП. Негативной стороной методики является увеличение шума в выходном сигнале. Фактически, ошибка квантования размазывается по нескольким соседним отсчётам. Такой подход является более желательным, чем простое округление до ближайшего дискретного уровня. В результате использования методики подмешивания псевдослучайного сигнала мы имеем более точное воспроизведение сигнала во времени. Малые изменения сигнала могут быть восстановлены из псевдослучайных скачков МЗР путём фильтрации. Кроме того, если шум детерминирован (амплитуда добавляемого шума точно известна в любой момент времени), то его можно вычесть из оцифрованного сигнала, предварительно увеличив его разрядность, тем самым почти полностью избавиться от добавленного шума.
Звуковые сигналы очень малых амплитуд, оцифрованные без псевдослучайного сигнала, воспринимаются на слух очень искажёнными и неприятными. При подмешивании псевдослучайного сигнала истинный уровень сигнала представлен средним значением нескольких последовательных отсчётов.
Однако с 2009 года, в связи с удешевлением 24-битных АЦП, имеющих даже без dither’а динамический диапазон более 120 дБ, что на несколько порядков превышает полный воспринимаемый человеком диапазон слуха, данная технология потеряла актуальность в звукотехнике. При этом она используется в ВЧ- и СВЧ-технике, где битность АЦП обычно мала из-за высокой частоты дискретизации.
Похожий процесс, также называемый dither или диффузия ошибок, применяется для представления полутонов изображений в компьютерной графике при малом количестве бит на пиксел. При этом изображение становится зашумлённым, но визуально воспринимается реалистичнее, чем то же изображение, полученное простым квантованием.
Как правило, сигналы оцифровываются с минимально необходимой частотой дискретизации из соображений экономии, при этом шум квантования является белым, то есть его спектральная плотность мощности равномерно распределена во всей полосе. Если же оцифровать сигнал с частотой дискретизации, гораздо большей, чем по теореме Котельникова — Шеннона, а затем подвергнуть цифровой фильтрации для подавления спектра вне частотной полосы исходного сигнала, то отношение сигнал/шум, будет лучше, чем при использовании всей полосы. Таким образом можно достичь эффективного разрешения большего, чем разрядность АЦП.
Передискретизация также может быть использована для смягчения требований к крутизне перехода от полосы пропускания к полосе подавления антиалиасингового фильтра. Для этого сигнал оцифровывают, например, на вдвое большей частоте, затем производят цифровую фильтрацию, подавляя частотные компоненты вне полосы исходного сигнала, и, наконец, понижают частоту дискретизации путём децимации.
Ниже перечислены основные способы построения электронных АЦП:
Параллельные АЦП прямого преобразования — самые быстрые, но обычно имеют разрешение не более 8 бит, так как влекут за собой большие аппаратные затраты ( компараторов). АЦП этого типа имеют очень большой размер кристалла микросхемы, высокую входную ёмкость, и могут выдавать кратковременные ошибки на выходе. Часто используются для видео или других высокочастотных сигналов, а также широко применяются в промышленности для отслеживания быстро изменяющихся процессов в реальном времени.
Неэлектронные АЦП обычно строятся на тех же принципах.
Как правило, выпускаются в виде микросхем.
Для большинства АЦП разрядность составляет от 6 до 24 бит, частота дискретизации до 1 МГц. Мега- и гигагерцовые АЦП также доступны (февраль 2002). Мегагерцовые АЦП требуются в цифровых видеокамерах, устройствах видеозахвата и цифровых ТВ-тюнерах для оцифровки полного видеосигнала. Коммерческие АЦП обычно имеют выходную ошибку от ±0,5 до ±1,5 МЗР.
Один из факторов увеличивающих стоимость микросхем — это количество выводов, поскольку они вынуждают делать корпус микросхемы больше, и каждый вывод должен быть присоединён к кристаллу. Для уменьшения количества выводов часто АЦП, работающие на низких частотах дискретизации, имеют последовательный интерфейс. Применение АЦП с последовательным интерфейсом зачастую позволяет увеличить плотность монтажа и создать плату с меньшей площадью.
Часто микросхемы АЦП имеют несколько аналоговых входов, подключённых внутри микросхемы к единственному АЦП через аналоговый мультиплексор. Различные модели АЦП могут включать в себя устройства выборки-хранения, инструментальные усилители или высоковольтный дифференциальный вход и другие подобные цепи.
АЦП встроены в большую часть современной звукозаписывающей аппаратуры, поскольку обработка звука делается, как правило, на компьютерах; даже при использовании аналоговой записи АЦП необходим для перевода сигнала в PCM-поток, который будет записан на компакт-диск.
Современные АЦП, используемые в звукозаписи, могут работать на частотах дискретизации до 192 кГц. Многие люди, занятые в этой области, считают, что данный показатель избыточен и используется из чисто маркетинговых соображений (об этом свидетельствует теорема Котельникова — Шеннона). Можно сказать, что звуковой аналоговый сигнал не содержит столько информации, сколько может быть сохранено в цифровом сигнале при такой высокой частоте дискретизации, и зачастую для Hi-Fi-аудиотехники используется частота дискретизации 44,1 кГц (стандартная для компакт-дисков) или 48 кГц (типична для представления звука в компьютерах). Однако широкая полоса упрощает и удешевляет реализацию антиалиасинговых фильтров, позволяя делать их с меньшим числом звеньев или с меньшей крутизной в полосе заграждения, что положительно сказывается на фазовой характеристике фильтра в полосе пропускания.
Аналого-цифровые преобразователи для звукозаписи имеют широкий диапазон цен — от 100 до 10 тыс. долл. и выше за двухканальный АЦП.
АЦП для звукозаписи, используемые в компьютерах, бывают внутренние и внешние. Также существует свободный программный комплекс PulseAudio для Linux, позволяющий использовать вспомогательные компьютеры как внешние ЦАП/АЦП для основного компьютера с гарантированным временем запаздывания.
Аналого-цифровое преобразование используется везде, где требуется принимать аналоговый сигнал и обрабатывать его в цифровой форме.
dic.academic.ru
Аналого-цифровые преобразователи (АЦП)
|
Рис. 1. Идеальная (сплошная зеленая линия) и реальная функция преобразования АЦП |
Интегральная нелинейность Iint характеризует отклонение реальной функции преобразования (штрихпунктир) от идеальной линейной (сплошная линия) (см. рис. 1). Интегральная нелинейность Iint определяется следующим образом
Iint% = 100(Vnom — Vact)/Vmax,
где (Vnom — Vact) — максимальное
отклонение от линейности.
Дифференциальная нелинейность Idif
характеризует неоднородность ширин каналов АЦП и определяется следующим образом.
Idif% = 50(Wmax — Wmin)/Wavg,
где Wmax, Wmin и Wavg —
максимальная, минимальная и средняя ширины каналов.
У качественных АЦП дифференциальная нелинейность ~1%, а
интегральная <0.05% при 12-разрядном (4096 каналов) преобразовании.
В промышленной электронике было разработано много методов преобразования аналоговых величин в цифровой код. Однако в ядерной электронике используются только некоторые из них. В основном используются АЦП вилкинсоновского типа и АЦП поразрядного взвешивания. В последнее время в ядерной электронике стали использоваться и параллельные АЦП, входящие в состав цифровых процессоров сигналов.
|
Рис. 2. Сигналы в АЦП во время измерения. |
|
| а) | |
| б) | |
Рис. 3. Циклы работы АЦП вилкинсоновского типа. |
Принцип работы АЦП вилкинсоновского типа (D.H Wilkinson)
основан на преобразовании амплитуда — время. Входной импульс поступает на
дискриминатор нижнего уровня, уровень дискриминации которого обычно
устанавливается выше уровня шумов (см. рис. 2). Когда уровень входного сигнала
достигнет уровня дискриминации, линейные ворота открываются, и накопительная
емкость C соединяется с входом (рис. 3а). Начинается заряд емкости до
амплитудного значения входного сигнала. Когда емкость зарядится, линейные
ворота закрываются, накопительная емкость отсоединяется от входа и
присоединяется к источнику постоянного тока (рис. 3б). Начинается линейный
разряд емкости. В это же время таймирующий (времязадающий) генератор
подключается к адресному счетчику, который начинает считать импульсы
таймирующего генератора. Частота генератора обычно 100 — 200 МГц. Когда емкость
полностью разрядится, накопительная емкость отсоединяется от источника
постоянного тока, а таймирующий генератор отсоединяется от адресного счетчика
(рис. 3в) и начинается цикл записи в память. Число сосчитанных во время разряда
емкости импульсов определяет время разряда накопительной емкости, а время
линейного разряда пропорционально амплитуде анализируемого импульса. Полученное
в адресном счетчике число (код) используется для адресации соответствующей
ячейки памяти, куда добавляется единица.
Мертвое время у
этого АЦП
складывается из
= Tr + Tc + Tmc,
где Tr — время достижения максимума импульса, Tc —
время конверсии, Tmc — время цикла записи. Времена Tr и Tmc
около 1 мкс. Основной вклад в мертвое время вносит время конверсии, которое
зависит от амплитуды входного импульса или соответственно от номера канала n (Tc = nTgen),
где Tgen — период таймирующего генератора. Так Tc = 10 мкс
при частоте генератора 100 МГц и n = 1000.
У АЦП вилкинсоновского типа малые интегральная и
дифференциальная нелинейности, однако относительно большое мертвое время,
которое к тому же зависит от амплитуды.
Принцип работы АЦП поразрядного взвешивания заключается в последовательном сравнении амплитуды анализируемого сигнала (Vin) с напряжением цифро-аналогово преобразователя (VDAC), уровень которого задается регистром.
| Номер канала | Состояние регистра | Диапазон амплитуд |
| 8 | 000 | Vmax>V>7/8(Vmax) |
| 7 | 111 | 7/8(Vmax)>V>6/8(Vmax) |
| 6 | 110 | 6/8(Vmax)>V> 5/8(Vmax) |
| 5 | 101 | 5/8(Vmax)>V> 4/8(Vmax) |
| 4 | 100 | 4/8(Vmax)>V> 3/8(Vmax) |
| 3 | 011 | 3/8(Vmax)>V> 2/8(Vmax) |
| 2 | 010 | 2/8(Vmax)>V> 1/8(Vmax) |
| 1 | 001 | 1/8(Vmax)>V |
Для простоты рассмотрим работу трехразрядного АЦП. В
начальном состоянии в старшем бите регистра установлена единица (100). Согласно
этой установке цифро-аналоговый преобразователь (ЦАП) устанавливает напряжение
равное половине динамического диапазона (VDAC = Vmax/2).
Это напряжение сравнивается с величиной измеряемой амплитуды Vin.
Если Vin > Vmax/2, то в регистре следующий бит (110), а в
ЦАП соответственно устанавливается напряжение 6/8(Vmax). Если Vin < Vmax/2,
то в регистре старший бит зануляется, а единица устанавливается в следующем бите
(010), что соответствует напряжению ЦАП 2/8(Vmax). После еще одного
(третьего) сравнения преобразование заканчивается, при этом |Vin — VDAC| < Vmax/8,
а конечное состояние регистра определяет адрес ячейки памяти, куда добавляется
единица. В 12-разрядном АЦП (4096 каналов) проводится соответственно 12
сравнений. Время преобразования и, соответственно, мертвое время АЦП
поразрядного взвешивания не зависит от амплитуды как в АЦП вилкинсоновского
типа, а определяется количеством сравнений, т.е. разрядностью. Мертвое время АЦП
поразрядного взвешивания ~1 мкс. Дифференциальная нелинейность таких АЦП
несколько хуже, чем у АЦП вилкинсоновского типа.
Улучшить дифференциальную нелинейность можно с помощью
метода сдвигающейся шкалы (sliding scale linearization). Его также называют
методом статистического разравнивания. Сущность этого метода заключается в
следующем. К входному сигналу добавляется ступенька напряжения примерно равная
ширине канала, к следующему входному сигналу — удвоенная ступенька и т.д.
m раз, после чего система возвращается в исходное состояние*. В адресном
регистре каждый раз формируется число, которое на m больше, чем должно было бы
быть без добавления «ступенек». Затем из адресного регистра это число m
вычитается. Таким образом, происходит статистическое усреднение ширины каналов,
и дифференциальная нелинейность уменьшается в (m+1) раз.
__________________________________________________
* Это похоже на измерение расстояний при помощи линейки, нулевая отметка у
которой от измерения к измерению сдвигается на одно деление.
Успехи микроэлектроники позволили создать параллельные АЦП, с помощью которых можно снимать профили аналоговых сигналов, т.е. получать развертку сигнала во времени в цифрах. В параллельном АЦП содержится большое количество (2k), где k — разрядность АЦП, параллельно включенных дискриминаторов с последовательно увеличивающимися порогами дискриминации
Vn = Vn-1 + V.
Количество сработавших дискриминаторов собственно и есть результат преобразования аналоговой информации (напряжения) в цифру. Неоспоримым преимуществом таких АЦП является то, что они очень быстрые. Параллельные АЦП в частности нашли применение в цифровых процессорах спектрометрических сигналов. Для большинства применений такие АЦП должны иметь 12 разрядов и оцифровывать с частотой ~100 МГц. Для временных измерений с быстрыми сцинтилляторами требуются 8-разрядные АЦП с частотой ~1 ГГц.
[ОГЛАВЛЕНИЕ]
nuclphys.sinp.msu.ru
В большинстве случаев получаемый непосредственно от источника информации сигнал оказывается представленным в форме непрерывно меняющегося по своему значению напряжения либо тока (рис. 10.69). Таков, в частности, характер электрического сигнала, соответствующего телефонным, телевизионным и другим видам сообщения. Для передачи таких сообщений по линии связи или для их обработки (например, при отфильтровании помех) могут быть использованы две формы: аналоговая или цифровая. Аналоговая форма предусматривает оперирование со всеми значениями сигнала, цифровая форма с отдельными его значениями, представленными в форме кодовых комбинаций.
Преобразование сигналов из аналоговой формы в цифровую выполняется в устройстве, называемом аналого-цифровым преобразователем (АЦП).
В преобразователе сигналов из аналоговой формы в цифровую можно выделить следующие процессы: дискретизацию, квантование, кодирование. Рассмотрим сущность этих процессов. При этом для определенности в последующем изложении будем считать, что преобразование в цифровую форму осуществляется над сигналом, представленным в форме меняющегося во времени напряжения.
Дискретизация непрерывных сигналов.
Процесс дискретизации заключается в том, что из непрерывного во времени сигнала выбираются отдельные его значения, соответствующие моментам времени, следующим через определенный временной интервал Т (на рис. 10.69 моменты). Интервал Т называется тактовым интервалом времени, а моменты временив которые берутся отсчеты, — тактовыми моментами времени.
Дискретные значения сигнала следует отсчитывать с таким малым тактовым интервалом Т, чтобы по ним можно было бы восстановить сигнал в аналоговой форме с требуемой точностью. 14.1.2. Квантование и кодирование. Сущность этих операций заключается в следующем. Создается сетка так называемых уровней квантования (рис. 10.70), сдвинутых друг относительно друга на •величину Д, называемую шагом квантования. Каждому уровню квантования можно приписать порядковый номер (0, 1, 2, 3 и т.д.). Далее, полученные в результате дискретизации значения исходного аналогового напряжения заменяются ближайшими к ним уровнями квантования. Так, на диаграмме рис. 10.70 значение напряжения в момент заменяется ближайшим к нему уровнем квантования с номером 3, в тактовый моментзначение напряжения ближе к уровню 6 и заменяется этим уровнем и т. д.
Описанный процесс носит название операции квантования, смысл которого состоит в округлении значений аналогового напряжения, выбранных в тактовые моменты времени. Как и всякое округление, процесс квантования приводит к погрешности (к ошибкам квантования) в представлении дискретных значений напряжения, создавая так называемый шум квантования. При проектировании АЦП стремятся снизить шум квантования до такого уровня, при котором он еще обеспечивает требуемую точность представления сигнала. Подробнее шум квантования будет рассмотрен далее.
рис 10.70
рис 10.71
Следующая операция, выполняемая при аналого-цифровом преобразовании сигналов, — кодирование. Смысл ее состоит в следующем. Округление значения напряжения, осуществляемое при операции квантования, позволяет эти значения представлять числами — номерами соответствующих уровней квантования. Для диаграммы, представленной на рис. 10.70, образуется последовательность чисел: 3, 6, 7, 4, 1, 2 и т.д. Далее, получаемая таким образом последовательность чисел представляется двоичным кодом.
Вернемся к искажениям, связанным с процессом квантования, названным шумом квантования. При телефонной связи шум квантования воспринимается ухом человека действительно в виде шума, сопровождающего речь.
Так как в процессе квантования значение напряжения в каждый тактовый момент времени округляется до ближайшего уровня квантования, ошибка в представлении значений напряжения оказывается в пределах.
Следовательно, чем больше шаг квантования, тем больше ошибки квантования. Считая, что в указанных пределах любые значенияравновероятны, можно получить выражение среднеквадратичного значения ошибки квантования.
рис 10.72
рис 10.73
Уменьшение шума квантования достигается только уменьшением шага квантования . Так как- промежуток между соседними уровнями квантования, то с уменьшением, очевидно, должно возрасти число уровней квантования в заданном диапазоне значений напряжения. Пусть- ширина диапазона изменений напряжения. Тогда требуемое число уровней квантова.ния. Обычнои.
Отсюда видно, что уменьшение шума квантования путем уменьшения приводит к увеличению числа уровней квантования N. Это увеличивает число разрядов при представлении номеров уровней квантования двоичными кодами.
При организации телефонной связи номера уровней квантования обычно выражают семи-восьмиразрядными двоичными числами, а число уровней квантования оказывается равным .
Наряду с рассмотренными выше погрешностями — погрешностями квантования — при аналого-цифровом преобразовании возникают погрешности аппаратурные, связанные с неточностью работы отдельных узлов АЦП. Эти погрешности будут выявляться далее при рассмотрении различных схемных построений АЦП.
studfiles.net