
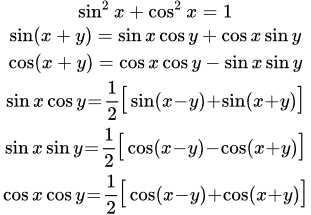
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
|BD| — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.
Определение
Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
;
;
.
;
;
.
Функции y = sin x и y = cos x периодичны с периодом 2π.
Функция синус – нечетная. Функция косинус – четная.
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | –1 ≤ y ≤ 1 | –1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = –1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Далее мы полагаем, что – целое число.
;
;
;
.
;
;
;
.
; .
При , имеем:
; .
При :
; .
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
;
;
;
; . Вывод формул > > >
Производные n-го порядка:
; .
;
См. также раздел Таблица неопределенных интегралов >>>
{ –∞ < x < +∞ }
{ –∞ < x < +∞ }
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Вычислите с точностью [latex]\varepsilon[/latex] значение функции [latex]f\left( x \right) = \text{sh}x[/latex]. При вычислениях допустимо использовать только арифметические операции.
В одной строке задано два числа [latex]x[/latex] и [latex]E[/latex].
В одной строке вывести значение функции [latex]f\left( x \right) = \text{sh}x[/latex] и [latex]\text{sinh}x[/latex] (для проверки).
[latex]\text{sh} \left( x \right) = x — \frac {x^{3}}{3!}+\frac{x^{5}}{5!} — \cdots = \displaystyle\sum_{n=0}^{\infty}\frac{1}{(2n+1)!}x^{ 2n+1 },x\in{C}[/latex]
| Входные данные | Выходные данные (мои и стандартной функции) |
| 1.57 1e-10000 | 2.2993 2.2993 |
| 3.14 1e-100000 | 11.5303 11.5303 |
| 0 0.1 | 0 0 |
| 1.05 1e-1000 | 1.25386 1.25386 |
| 0.785 0 | 0.868144 0.868144 |
| 0.52 0.01 | 0.543435 0.543754 |
#include <iostream> #include <cmath> using namespace std; int main() { int i=0; double x, E; cin >> x >> E; double sh=x, a=x; while((a*=(x*x/(2*i+2)/(2*i+3)))>E) { sh+=a; i++; } cout << sh << ‘ ‘ << sinh(x); return 0; } |
cpp.mazurok.com
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
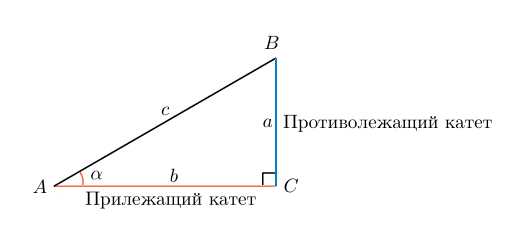
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
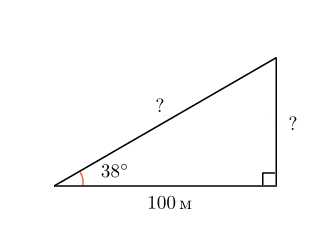
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
Поскольку , .
2. В треугольнике угол равен , , . Найдите .
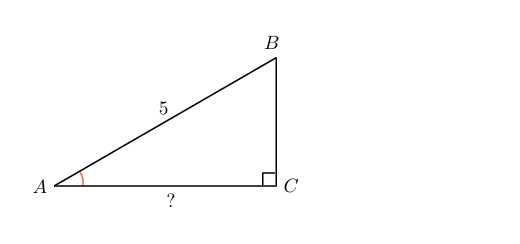
Имеем:
Отсюда
Найдем по теореме Пифагора.
Задача решена.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
1. Определения синуса, косинуса, тангенса и котангенса угла.
Синус угла (обозначается ) – ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинус угла (обозначается ) – абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенс угла (обозначается ) – отношение синуса угла к его косинусу, т.е.
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :
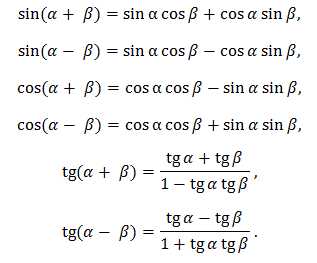
umath.ru
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функцийСинус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Опред
zaochnik.com
subjects:mathematics:тригонометрические_выражения_и_формулы
Отметим на координатной оси Ох справа от точки О точку А и построим окружность с центром в точке О и радиусом ОА (так называемым начальным радиусом).
Рис.1
Пусть при повороте на угол a против часовой стрелки начальный радиус ОА переходит в радиус ОВ.
Тогда:
Синусом (sin α) угла α называется отношение ординаты точки В к длине радиуса.
Косинусом (cos α) угла α называется отношение абсциссы точки В к длине радиуса.
Тангенсом (tg α) угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом (ctg α) угла α называется отношение абсциссы точки В к ее ординате.
Секанс определяется как sec α = 1/(cos α)
Косеканс определяется как cosec α = 1/(sin α)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x
Если координаты точки В равны x и y, то:
$$\sin{\alpha} = \frac{y}{R}\;;\; \cos{\alpha} = \frac{x}{R}\;;\; {\rm tg}\, \alpha = \frac{y}{x}\;;\; {\rm ctg}\, \alpha = \frac{x}{y}$$
Приведем таблицу значений тригонометрических функций некоторых углов (прочерк сделан, когда выражение не имеет смысла):
| Таблица значений sin α, cos α, tg α, ctg α | ||||||||
| 0º 0 рад | 30º $$\frac{\pi}{6}$$ | 45º $$\frac{\pi}{4}$$ | 60º $$\frac{\pi}{3}$$ | 90º $$\frac{\pi}{2}$$ | 180º $$\pi$$ | 270º $$\frac{3\pi}{2}$$ | 360º $$2\pi$$ | |
|---|---|---|---|---|---|---|---|---|
| $$\sin \alpha$$ | 0 | $$\frac{1}{2}$$ | $$\frac{\sqrt{2}}{2}$$ | $$\frac{\sqrt{3}}{2}$$ | 1 | 0 | -1 | 0 |
| $$\cos \alpha$$ | 1 | $$\frac{\sqrt{3}}{2}$$ | $$\frac{\sqrt{2}}{2}$$ | $$\frac{1}{2}$$ | 0 | -1 | 0 | 1 |
| $${\rm tg}\, \alpha$$ | 0 | $$\frac{1}{\sqrt{3}}$$ | 1 | $$\sqrt{3}$$ | — | 0 | — | 0 |
| $${\rm ctg}\, \alpha$$ | — | $$\sqrt{3}$$ | 1 | $$\frac{1}{\sqrt{3}}$$ | 0 | — | 0 | — |
Свойства синуса (sin), косинуса (cos), тангенса(tg) и котангенса(ctg):
Определение знака
Если α-угол I или II координатной четверти, то sin α > 0;
Если α-угол III или IV координатной четверти, то sin α < 0;
Если α-угол I или IV координатной четверти, то cos α > 0;
Если α-угол II или III координатной четверти, то cos α < 0;
Если α-угол I или III координатной четверти, то tg α > 0 и ctg α > 0;
Если α-угол II или IV координатной четверти, то tg α < 0 и ctg α < 0.
Синус, тангенс и котангенс — нечетные функции; косинус — четная функция.
Для чётной функции справедливо равенство: y(-x) = y(x). Примеры чётных функций: y = cos(x), y = x2.
Для НЕчётной функции справедливо равенство: y(-x) = -y(x). Примеры НЕчётных функций: y = sin(x), y = x.
При изменении угла на целое число оборотов значения тригонометрических функций не меняются.
1 радиан — это мера центрального угла, которому соответствует длина дуги, равная длине радиуса окружности.
Связь радианов с градусами: $1° =\frac{\pi}{180}\text{рад; 1 рад }=\frac{180°}{\pi}$.
| X | $\frac{\pi}{2}-\alpha$ | $\frac{\pi}{2}+\alpha$ | $\pi-\alpha$ | $\pi+\alpha$ | $\frac{3\pi}{2}-\alpha$ | $\frac{3\pi}{2}+\alpha$ | $2\pi-\alpha$ | $2\pi+\alpha$ |
|---|---|---|---|---|---|---|---|---|
| sin x | cos α | cos α | sin α | -sin α | -cos α | -cos α | -sin α | sin α |
| cos x | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg x | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg x | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Формулы двойного угла или двойного аргумента:
Формулы половинного аргумента (для sin и cos — формулы понижения степени):
Один из способов использования: свести всё к tg(x/2) и путём замены получить обычное алгебраическое выражение.
subjects/mathematics/тригонометрические_выражения_и_формулы.txt · Последние изменения: 2014/02/26 22:10 — ¶
www.wiki.eduvdom.com
Многочлены Чебышева, как упоминалось в другом ответе, являются многочленами, где наибольшее различие между функцией и полиномом как можно меньше. Это отличный старт.
В некоторых случаях максимальная ошибка — это не то, что вас интересует, а максимальная относительная ошибка. Например, для синусоидальной функции ошибка вблизи x = 0 должна быть намного меньше, чем для больших значений; вам нужна небольшая относительная ошибка. Таким образом, вы вычисляете полином Чебышева для sin x/x и умножаем этот многочлен на x.
Затем вам нужно выяснить, как оценить многочлен. Вы хотите оценить его таким образом, чтобы промежуточные значения были небольшими, и поэтому ошибки округления небольшие. В противном случае ошибки округления могут стать намного большими, чем ошибки в полиноме. И с функциями, такими как функция синуса, если вы небрежны, возможно, результат, который вы вычисляете для sin x, больше, чем результат для sin y, даже когда x < у. Поэтому необходим тщательный выбор порядка расчета и вычисления верхних границ погрешности округления.
Например, sin x = x — x ^ 3/6 + x ^ 5/120 — x ^ 7/5040… Если вы наивно вычисляете sin x = x * (1 — x ^ 2/6 + x ^ 4/120 — x ^ 6/5040…), то эта функция в круглых скобках уменьшается, и произойдет, что если y — следующее большее число к x, то иногда sin y будет меньше, чем sin x. Вместо этого вычислите sin x = x — x ^ 3 * (1/6 — x ^ 2/120 + x ^ 4/5040…), где этого не может быть.
При расчете полиномов Чебышева, например, обычно нужно округлить коэффициенты до двойной точности. Но в то время как полином Чебышева оптимален, полином Чебышева с коэффициентами, округленными до двойной точности, не является оптимальным полиномом с коэффициентами двойной точности!
Например, для sin (x), где вам нужны коэффициенты для x, x ^ 3, x ^ 5, x ^ 7 и т.д., вы делаете следующее: Вычислите наилучшее приближение sin x с полиномом (ax + bx ^ 3 + cx ^ 5 + dx ^ 7) с более высокой, чем двойной точностью, затем округляя до двойной точности, давая A. Разница между a и A будет довольно большой. Теперь вычислим наилучшее приближение (sin x — Ax) с полиномом (b x ^ 3 + cx ^ 5 + dx ^ 7). Вы получаете разные коэффициенты, потому что они приспосабливаются к разности между a и A. Круглый b для двойной точности B. Тогда приближенно (sin x — Ax — Bx ^ 3) с полиномом cx ^ 5 + dx ^ 7 и т.д. Вы получите полином, который почти так же хорош, как и оригинальный полином Чебышева, но намного лучше, чем Чебышев, округленный до двойной точности.
Далее следует учитывать ошибки округления при выборе полинома. Вы нашли многочлен с минимальной ошибкой в полиноме, игнорируя ошибку округления, но вы хотите оптимизировать ошибку полинома плюс округление. Когда у вас есть полином Чебышева, вы можете рассчитать границы ошибки округления. Скажем, что f (x) — ваша функция, P (x) — многочлен, а E (x) — ошибка округления. Вы не хотите оптимизировать | f (x) — P (x) |, вы хотите оптимизировать | f (x) — P (x) +/- E (x) |. Вы получите немного другой полином, который пытается сохранить ошибки полинома, где ошибка округления велика, и немного ослабляет ошибки полинома, где ошибка округления мала.
Все это позволит вам легко округлять ошибки не более чем в 0,55 раза по сравнению с последним битом, где +, -, *,/имеют ошибки округления не более 0,50 раз больше последнего бита.
qaru.site