8-900-374-94-44
Режекторный фильтр — не частый гость в наших краях. Зверь редкий, нелюдимый, но для радиолюбительского хозяйства — весьма полезный. Внешне напоминает полосовых собратьев, но охотится исключительно за сигналами вокруг центральной частоты и мало активен на частотах, выходящих за пределы отведённого ему диапазона.
Для начала определимся с терминологией.
Полосно-заграждающий фильтр (он же — режекторный фильтр, он же — фильтр-пробка) — электронный или любой другой фильтр,
не пропускающий сигналы со входа на выход в определённой полосе частот, но имеющий близкий к единице коэффициент передачи при
более низких и более высоких частотах.
Эта полоса подавления характеризуется шириной полосы заграждения и расположена вокруг центральной частоты подавления fо.
Заграждающий фильтр, предназначенный для подавления одной определённой частоты, называется узкополосным заграждающим фильтром
или фильтром-пробкой.
Для описания режекторных фильтров используют следующие параметры:
центральная частота подавления fо;
две граничных частоты – нижняя fн и верхняя fв, при которых Кu = 0,7mах;
диапазон частот Δf = fв − fн, называемый полосой задержания;
параметр Q = (fв + fн)/(2Δf), называемый добротностью.
Простейшие Т-образные фильтры и их амплитудно-частотная характеристика приведены на Рис.1.
Рис.1
Центральная частота подавления этих фильтров рассчитывается по формуле: fо = 1/(2π*R*C) при R1=R2=R, C1=C2=C. Глубина режекции — всего 10 дБ, а полоса задержания составляет значение, в 5-6 раз превышающее fо.
Именно в силу указанных выше хилых характеристик — подобные простейшие цепи уступили позиции двойным Т-образным RC-фильтрам (Рис.2), часто называемым 2ТФ.
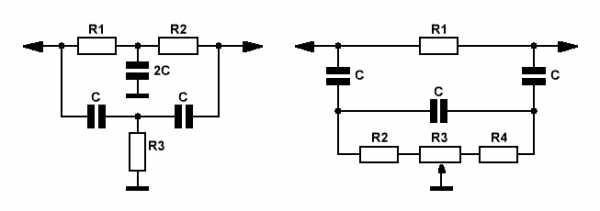
Рис.2 Рис.3
Двойной Т-образный RC-фильтр при определённых условиях (симметрия моста, точный подбор элементов, согласование входа и выхода) почти полностью подавляет центральную частоту fo. Глубина режекции (подавления частоты fo) при работе на высокоомную нагрузку достигает 50 дБ. Добротность Q — около 0,3.
На Рис.2 приведена классическая схема двойного Т-образного режекторного фильтра, на Рис.3 — с возможностью плавной регулировки центральной частоты подавления.
Начнём с нерегулируемой схемы.
Обычно выбираются следующие соотношения элементов R2=R1, R3=R1/2.
Номиналы этих резисторов должны быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.
Ничего не изменилось, центральная частота вычисляется по формуле fо = 1/(2π*R*C).
РИСУЕМ ТАБЛИЦУ ДЛЯ ДВОЙНЫХ Т-ОБРАЗНЫХ RC-ФИЛЬТРОВ
При желании ввести регулировку центральной частоты подавления fо с диапазоном перекрытия по частоте более чем в 2 раза, при сохранении параметров, присущих двойным Т-образным режекторным фильтрам, имеет смысл воспользоваться схемой, приведённой на Рис.3.
Значение резистора R1 должно в 6 раз превышать суммарную величину R2, R3 и R4, поэтому его следует выбирать номиналом — не менее 100 кОм.
Формула для расчёта частоты подавления fо = 1/(2πС√3×R3_1×R3_2),
где R3_1 — сумма сопротивлений слева от регулирующего вывода R3, а R3_2 — справа.
Рисуем таблицу и для таких фильтров.
ТАБЛИЦА ДЛЯ ПЕРЕСТРАИВАЕМЫХ РЕЖЕКТОРНЫХ RC-ФИЛЬТРОВ
Дальнейшего улучшения параметров режекторных фильтров можно добиться введением в схему на Рис.2
положительной обратной связи, подаваемой в точки, идущие к земляной шине.
В результате подобных действий фильтры становятся активными и приобретают следующий вид.
Рис.4 Рис.5
На Рис.4 приведена схема активного режекторного фильтра на основе простого двойного Т-моста.
Значение добротности определяется отношением значений резисторов K=R5/R4. При изменении этого отношения в диапазоне К=0.01-0.2 добротность Q меняется практически линейно и принимает значения от 30 до 2. Дальнейшее увеличение параметра К не приветствуется, в связи с ухудшением неравномерности АЧХ в полосе пропускания.
Для желающих же регулировать значение добротности в более широких пределах на Рис.5 приведена схема активного режекторного фильтра на двух операционных усилителях. Здесь переменный резистор R4 позволяет изменять добротность в пределах 50 — 0.3.
А при необходимости получить перестраиваемый по частоте активный режекторный фильтр, регулирующий вывод переменного резистора R3 на Рис.3, точно таким же образом подключается к выходу операционного усилителя. Результатом является схема, изображённая на Рис.6 .
Рис.6 Рис.7
На Рис.7 приведена схема режекторного фильтра, позволяющая регулировать как частоту подавления, так и добротность в широких пределах.
Обе таблицы для расчёта частотозадающих элементов остаются в силе!
Ну, да и хватит, на следующей странице будем мурыжить режекторные LC фильтры.
vpayaem.ru
Фильтр нижних частот (ФНЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.
Фильтр высших частот (ФВЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.
Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.
Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить исходя из коэффициента деления с импедансом Z.
Импеданс — комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ; Z = √(R² + X²) , где Х — реактивное сопротивление.
Тогда на выводах резистора напряжение UR будет составлять:
XC – реактивное сопротивление конденсатора, равное 1/2πfC
При равенстве R = XC на частоте f, выражение упростится сокращением
Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:
τ — постоянная времени цепи RC равна произведению RC
Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.
Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).
Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ) спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.
Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) — красная линия на рисунке, или фильтр высших частот (ФВЧ) — синяя линия.
Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.
Частоту f = 1/(2π τ) называют граничной частотой fгр или частотой среза fср фильтра.
Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Пост. времени τ RC и частота среза RC-фильтра |
Похожие страницы с расчётами:
Расчёт импеданса.
Расчёт резонансной частоты колебательного контура.
Расчёт компенсации реактивной мощности.
Замечания и предложения принимаются и приветствуются!
tel-spb.ru
Сложную отрицательную обратную связь можно использовать для построения полосовых фильтров. Соответствующая схема приведена на рис.4.2.
Рис.4.1. Амплитудно—частотная характеристика
полосового фильтра второго порядка
fР –резонансная (центральная) частота, определяемая выражением
fР = 
,
где fl –нижняя частота по уровню –3 дБ; fh –верхняя частота по уровню –3 дБ.
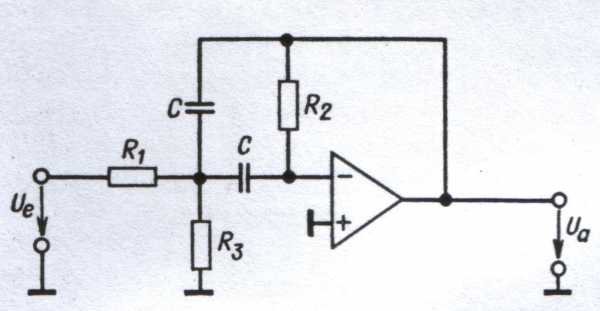
Рис.4.2. Полосовой фильтр со сложной отри-
цательной обратной связью. (фильтр Баттеворта)
Передаточная функция полосового фильтра имеет вид
f (S) =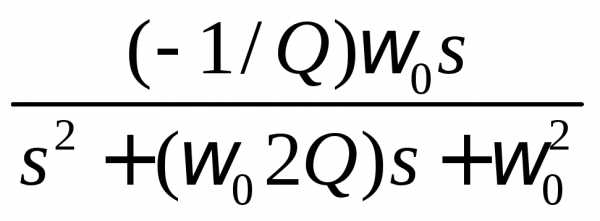 
,
(4.1)
где 
=2, 
s
– оператор Лапласа.
Отсюда находим резонансную частоту:
fР =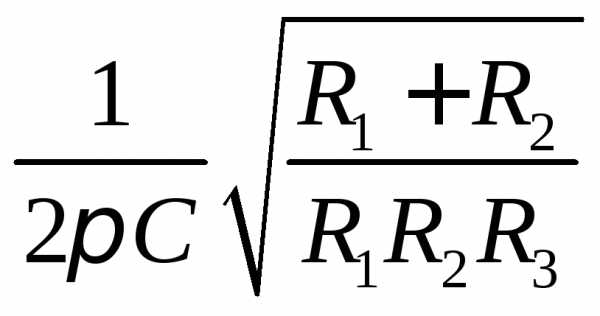 
.
(4.2), (резонансная частота)
Коэффициент передачи на резонансной частоте –АV = R2 / 2R1.
Добротность Q = R2CfР
Ширина полосы В = 1 / R2C. (4.4)
Подставив это выражение для резонансной частоты о передаточную функцию и приравняв соответствующие коэффициенты, получим остальные формулы для вычисления характеристик фильтра:
AV = R2 / 2R1 , (4.5.)
Q =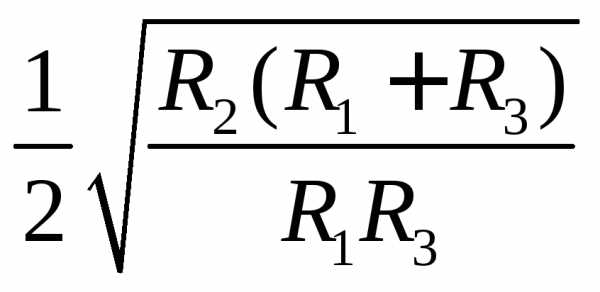
= R2CfР , (4.6)
из которых видно, что коэффициент передачи , добротность и резонансная частота рассматриваемого фильтра могут выбираться произвольно.
Выражение для полосы пропускания фильтра получим из формулы (4.6)
В = fР / Q = 1 / R2C (4.7)
Таким образом, величина В не зависит от R1 и R3. Из формулы (4.5) следует, что AV не зависит от R3. Поэтому можно изменять резонансную частоту fР , варьируя величину сопротивления R3 , что не приведет к изменению ширины пропускания фильтра и коэффициента передачи AV .
Основное уравнение можно записать из (4.1) в виде:
fР = 0,159 Q / R1C1 , (4.8)
и по соглашению
R2 = R1R3 / (4Q2R1—R3), R3 = 2R1 , C1=C2. (4.9)
Пример 4.1. Спроектируем фильтр, имеющий верхнюю частоту по уровню –3 дБ, равную 525 Гц, а нижнюю частоту по уровню –3 дБ, равную
475 Гц. Положим С2 = 1 мкФ.
fр = 
500
Гц (приблизительно)
Согласно (4.7 ),
Q = 500 / (525-475),
f = 500 / 50 = 10 (ширина полосы пропускания)
Согласно (4.9),
R1 = 0,159*10 / (500*1*10-6),
R1 = 3180 Ом,
По соглашению
R3 = 6360 Ом,
С1 = 1 мкФ,
R 3 = 3180*6380 / (4*102*3180—6380),
R3 =16 Ом
Электропитание
большинства электронных схем осуществляется
от стабилизированных источников
постоянного напряжения в пределах от
5В до 25В. Для питания ряда схем (например,
операционных усилителей) требуется
симметричное относительно общей точки
(«земли») напряжение 
±9В,
±12В или ±15В.
На рис.5.1 показан широко используемый в маломощных устройствах диодный выпрямитель переменного тока в сочетании с изолирующим сетевым трансформатором и емкостным фильтром.
Рис.5.1. Схема однофазного выпрямителя переменного тока
В таблице 5.1 приведены основные соотношения между напряжением и током
Таблица 5.1 Соотношения для схемы рис.5.1
Параметр | Соотношение |
Выходное напряжение Udc | 1,41Uac |
Входной ток Idc | 0,62Iac |
Входное напряжение Uac | 0,71Udc |
Входной ток Iac | 1,61Idc |
Минимальная емкость фильтрового конденсатора, мкФ*А | 2200Idc |
Для увеличения надежности схемы рекомендуется выбирать конденсатор с рабочим напряжением 2Udc .
Большинство источников электропитания включает в себя интегральный стабилизатор, позволяющий уменьшать пульсации напряжения и обеспечивающий возможность его регулирования. Для нормального функционирования регулятора на нем падает напряжение порядка 2 В. Учитывая нестабильность первичного источника (промышленная сеть, аккумуляторная батарея), необходимо выбирать напряжение на регуляторе в пределах от 3 до 6 В. Очевидно, чем выше это напряжение, тем большая мощность выделяется в регуляторе и тем труднее его охлаждать. Обычно
3 В ≤ UРЕГ ≤ 6 В
Если Udc – напряжение на входе регулятора, а UH –напряжение на нагрузке, то можно записать
UРЕГ = Udc – UH .
Мощность, выделяющаяся в регуляторе, определяется из соотношения
PРЕГ = IH UРЕГ = IH (Udc –UH),
где IH – ток нагрузки.
Пример 5.1. Требуется обеспечить напряжение 12 В на нагрузке, потребляющей ток 1 А. Первичная сеть переменного тока питается напряжением 220 В, которое может изменяться в пределах ±15%. В схеме используется стабилизатор К142 ЕН 12.
Тогда минимальное напряжение на стабилизаторе выбираем равным 3 В.
Тогда минимальное напряжение на выходе выпрямителя переменного напряжения тока при минимальном напряжении в первичной сети
Udc min = UРЕГ + UH = 3 + 12 = 15 B;
при максимальном напряжении в первичной сети
Udc max = 20,3 В.
В этом случае на стабилизаторе будет напряжение
UРЕГ = Udc –UH = 20,3 – 12 = 8,3 B/
При номинальном напряжении сети
Udc = 17,7 B.
напряжение регулятора
UРЕГ = Udc –UH = 17,7 –12 = 5,7 B.
Если в качестве выпрямителя использовать мостовую схему, то на диодах будет теряться напряжение около 1 В. Это нужно учесть при расчете трансформатора. Напряжение действующее напряжение на вторичной обмотке трансформатора
Udc = 0,71(Udc + 1B) = 0,71*18,7 = 13,3 B.
Максимальный ток вторичной обмотки трансформатора
Iac = IH (Udc max – UH) = 1 (20,3 – 12 ) = 8,3 Вт.
Конденсатор фильтра С1 выбираем К50—35 –2200 мкФ – 64 В.
Стабилизатор
необходимо установить на радиатор с
тепловым сопротивлением не выше 3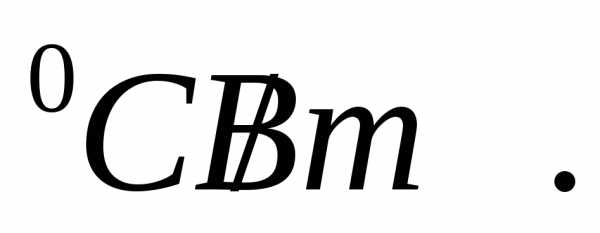 
Схема источника электропитания приведена
на рис.5.2.
Рис.5.2. Стабилизированный источник питания
studfiles.net
Не буду я описывать все страдания продвинутых аудиофилов по поводу необходимости (или, наоборот, вредоносности) использования этих девайсов в
составе высококачественной звуковоспроизводящей аппаратуры.
Пока братва дискутирует, современные производители дорогих многоканальных ресиверов всё чаще снабжают их встроенными эквалайзерами и
регуляторами фаз, которые в купе с выносным микрофоном производят анализ всех параметров воспроизведения звука в конкретном помещении
и автоматически выполняют все нужные коррекции для обеспечения наилучшего звучания.
А звукорежиссёры — виртуозы кнопок, фейдеров и крутилок? Они давно как оприходовали многоканальные эквалайзеры для обеспечения настройки
звука в студиях и концертных залах, имея целью ослабление влияния особенностей используемого помещения на звук.
Тут важно понимать, что эквалайзер не является продвинутым регулятором тембра, его главное предназначение — скорректировать
неравномерности АЧХ помещений и акустических систем. Скорректировали, возрадовались радостью весьма великою и забыли.
В этой статье мы поведём речь о графических эквалайзерах, есть ещё параметрические, но о них как-нибудь в другой раз.
Итак, преимущества графических эквалайзеров:
— Простое и быстрое воздействие на спектр.
— Одновременное изменение АЧХ разных участков спектра, как в плюс, так и в минус.
— Удобство применения и графическая наглядность.
Центральные частоты полосовых фильтров графического эквалайзера обычно равномерно распределены по октавным интервалам. Существуют эквалайзеры с «шагом» в одну октаву, половину, треть или одну шестую октавы. Никто не запрещает сделать это шаг и две, а то и больше октав, но это уже будет больше похоже на многополосный регулятор тембра.
Что нам нужно знать в первую очередь при расчёте полосовых фильтров графического эквалайзера, после того, как мы определились
с общим частотным диапазоном, обрабатываемым устройством, и количеством полос?
Добротность фильтров! Этот параметр в большинстве схем, увиденных мной в интернете, посчитан от вольного. Так, в наиболее
популярных среди радиолюбителей 10-ти полосных октавных эквалайзерах значение этой добротности, в зависимости от источника, принимало
замысловатые значения от 1 до 2, а ведь в умных книжках чёрным по белому написано Q=√ K/(K-1),
где К=21/M, а М — количество частотных полос на октаву. Для октавных фильтров М=1, подставляем,
делим и получаем Q=1,41.
Так вот, для того чтобы не допускать подобных просчётов, а заодно и филигранно уложить наши полосовые фильтры в заданный частотный
диапазон, весьма полезной окажется приведённая ниже программа.
Обратите внимание, что значения частот вводятся и выводятся в герцах, поэтому если Вы хотите указать 20кГц, надо вводить цифру 20000.
vpayaem.ru
При построении электронных схем достаточно часто используются фильтры полосового типа. Они широко применяются в резонансных контурах при построении схем приема и передачи радиосигнала и т.д. Для фильтрации частот низкого типа наиболее целесообразным является применение полосовых фильтров, в качестве активного элемента в которых выступает операционный усилитель.
Преимущественным достоинством полосовых фильтров, создаваемых на основе ОУ, является минимальное количество используемых компонентов. Поэтому такие фильтры легки в проектировании и построении, но при этом достаточно производительны.
Назначение и особенности полосовых фильтров
Полосовой фильтр создается с целью пропускания только частот заданного диапазона и погашения всех остальных частот. Основными характеристиками такого фильтра являются:
В идеале фильтр должен содержать резкое разграничение полос пропускания и затухания, обеспечивая беспрепятственное прохождения сигнала внутри полосы и полное его погашение вне данного диапазона.
На самом деле создать фильтр с идеальными характеристиками невозможно. В любом случае, сигнал, проходящий вне полосы пропускания, но в непосредственной близости к ней, будет погашаться только частично. Данную область именуют крутизной спада фильтра, ее измерение осуществляется в дБ затухания/октава. Чем уже область спада, тем эффективнее будет работать фильтр, что следует учитывать при его проектировке.
Расчет полосового фильтра
Построение полосового фильтра, обеспечивающего эффективную фильтрацию частот, – занятие достаточно сложное. Но вполне возможно создать фильтр на ОУ, оптимально совмещающий простую конструкцию и достаточно высокую производительность. Примером такого фильтра может послужить схема, содержащая помимо ОУ, 2 резистора и 3 конденсатора.
Максимальное и минимальное значение полосы пропускания определяются в зависимости от резонансной частоты (f) и добротности (Q):
fmax — fmin = f/Q .
Так, при значении f=20 Гц, Q=10, разница между максимальным и минимальным значением частот составляет 2 Гц, соответственно fmax=21 Гц, fmin=19 Гц.
Для упрощения расчетов в схеме лучше использовать конденсаторы одинаковой емкости. Допустим, C1=C2=C=1мкФ.
Для расчета сопротивления воспользуемся формулами:
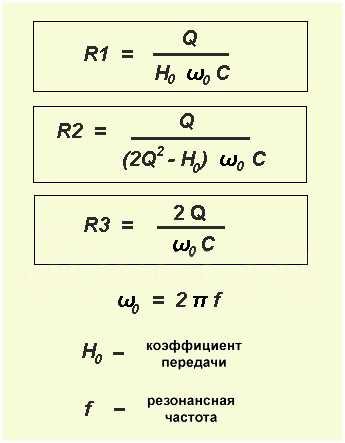
Выполним расчеты для случая H0= 5. Вообще, приступая к расчетам следует учесть, что для построения полосного фильтра, содержащего только один операционный усилитель, значение коэффициента усиления не должно быть более 5, а добротности – более 10.
Выполнив вычисления, получим: R1=15,9 кОм; R2=408кОм; R3=159,2 кОм.
Чем ближе будут характеристики резисторов и конденсаторов к полученным при расчете значениям, тем качественнее будет функционировать фильтр, созданный по вашей схеме.
В каталоге нашей компании можно приобрести полосовые фильтры, а также ознакомиться с их функциональными особенностями и характеристиками. Цены на представленные модели можно уточнить, связавшись с менеджером «СпецТехКонсалтинг».
pro-spec.ru
Полосовые фильтры используются во многих областях электроники. Особенно они широко используется в схемах радиоприема и радиопередачи, в частности в резонансных контурах. Однако и для низких частот, активный полосовой фильтр является эффективным средством выделения сигнала промежуточных частот. Для этих фильтров наиболее широко используемым активным элементом является операционный усилитель (ОУ).
Полосовые фильтры на ОУ легко проектировать и строить, поскольку для этого необходимо минимум компонентов. В дополнение к этому, они обеспечивают очень высокий уровень производительности.
Как следует из названия, полосовой фильтр фильтрует все частоты, пропуская только частоты находящиеся в определенном диапазоне. Все частоты за пределами данного частотного диапазона ослабляются.
Есть два основных параметра определяющие характеристики полосового фильтра: полоса пропускания, где фильтр пропускает сигналы и полоса затухания, в которой сигналы ослабляются.
Идеальный полосовой фильтр имеет ровную полосу пропускания (усиление и отсутствие затухания сигнала по всей полосе пропускания) и полное затухание вне полосы пропускания. Кроме того, переход из полосы пропускания абсолютно резкий.
Но на практике невозможно создать идеальный полосовой фильтр. Реальный фильтр неспособен полностью задержать все частоты за границами желаемого диапазона частот. В частности, имеется область в непосредственной близости у границы заданного диапазона, где сигнал частично ослабляется, но не отфильтровывается полностью. Эта область носит название крутизна спада фильтра, и измеряется в дБ затухания на октаву. Как правило, при проектировании, стремятся сделать данный спад как можно более узким, что позволяет получить фильтр максимально приближенным к заданным параметрам.
Расчет полосового фильтра может стать очень сложным занятием даже при использовании операционных усилителей. Тем не менее можно немного упростить методику расчета, и в то же время сохранить производительность полосового фильтра на ОУ на приемлемом уровне.
Данная схема и методика расчета представляют собой хороший баланс между производительностью и простотой конструкцией фильтра.
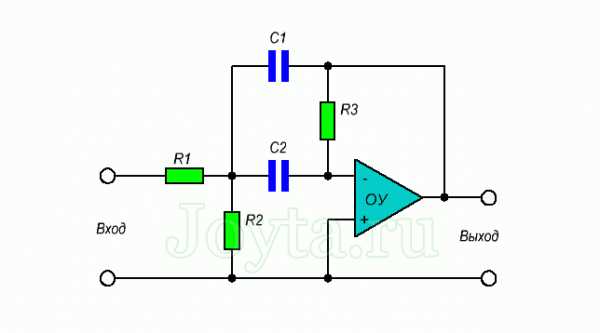
Из рисунка видно, что помимо операционного усилителя схема еще содержит два конденсатора и три резистора.
Входные данные:
Так как fmax – fmin = f / Q = 2Гц,
то полоса пропускания составит fmax = 21 Гц, fmin=19 Гц.
Будем исходить из того, что C1=C2=C=1мкФ
Тогда сопротивления резисторов можно рассчитать по следующим формулам:
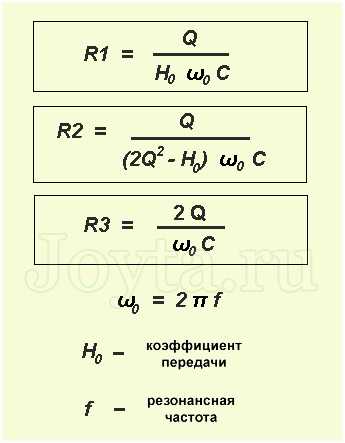
В нашем случае получим следующие результаты:
R1 = 10 / (5*2*3,14*20*0,000001) = 15,9 кОм
R2 = 10 / ((2*10*10-5)*2*3,14*20*0,000001) = 408 Ом
R3 = 2*10 / (2*3,14*20*0,000001) = 159,2 кОм
В схеме с одним операционным усилителем, желательно, чтобы коэффициент передачи не превышал 5 и добротность была не более 10. Для получения качественного фильтра параметры резисторов и конденсаторов должны как можно ближе соответствовать расчетным значениям.
www.joyta.ru
С целью снижения интермодуляционных искажений при звуковоспроизведении громкоговорители Hi-Fi систем составляют из низкочастотных, среднечастотных и высокочастотных динамических головок. Их подключают к выходам усилителей через разделительные фильтры, представляющие собой комбинации LC фильтров нижних и верхних частот.
Ниже приведена методика расчета трехполосного разделительного фильтра по наиболее распространенной схеме.
Частотная характеристика разделительного фильтра трехполосного громкоговорителя в общем виде показана на рис. 1. Здесь: N — относительный уровень напряжения на звуковых катушках головок: fн и fв — нижняя и верхняя граничные частоты воспроизводимой громкоговорителем полосы; fр1 и fр2 — частоты раздела.
В идеальном случае выходная мощность на частотах раздела должна распределяться поровну между двумя головками. Это условие выполняется, если на частоте раздела относительный уровень напряжения, поступающего на соответствующую головку, снижается на 3 дБ по сравнению с уровнем в средней части ее рабочей полосы частот.
Частоты раздела следует выбирать вне области наибольшей чувствительности уха (1… 3 кГц). При невыполнении этого условия, из-за разности фаз колебаний, излучаемых двумя головками на частоте раздела одновременно, может быть заметно «раздвоение» звука. Первая частота раздела обычно лежит в интервале частот 400… 800 Гц, а вторая — 4… 6 кГц. При этом низкочастотная головка будет воспроизводить частоты в диапазоне fн…fp1. среднечастотная — в диапазоне fp1… fр2 и высокочастотная — в диапазоне fр2…fв.
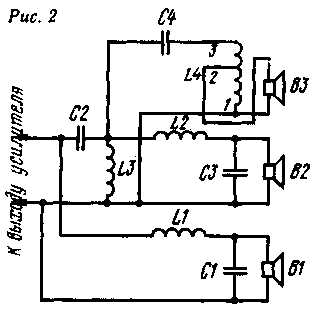
Один из распространенных вариантов электрической принципиальной схемы трехполосного громкоговорителя приведен на рис. 2. Здесь: B1 — низкочастотная динамическая головка, подключенная к выходу усилителя через фильтр нижних частот L1C1; В2 — среднечастотная головка, соединенная с выходом усилителя через полосовой фильтр, образованный фильтрами верхних частот C2L3 и нижних частот L2C3. На высокочастотную головку В3 сигнал подается через фильтры верхних частот C2L3 и C4L4.
Расчет емкостей конденсаторов и индуктивностей катушек производят исходя из номинального сопротивления головок громкоговорителя. Поскольку номинальные сопротивления головок и номинальные емкости конденсаторов образуют ряды дискретных значений, а частоты раздела могут варьироваться в широких пределах, то расчет удобно производить в такой последовательности. Задавшись номинальным сопротивлением головок, подбирают емкости конденсаторов из ряда номинальных емкостей (или суммарную емкость нескольких конденсаторов из этого ряда) такими, чтобы получившаяся частота раздела попадала в указанные выше частотные интервалы.
| Тип конденсатора | Емкость, мкФ |
| МБМ | 0,6 |
| МБГО, МВГП | 1; 2; 4; 10 |
| МБГП | 15; 26 |
| МБГО | 20; 30 |
{mospagebreak}Емкости конденсаторов фильтров С1…С4 для различных сопротивлений головок и соответствующие значения частот раздела приведены в табл 2.
| Zг,0м | 4.0 | 4.5 | 5.0 | 6.5 | 8.0 | 12,5 | 15 |
| С1,C2, мкф | 40 | 30 | 30 | 20 | 20 | 15 | |
| fp1, Гц | 700 | 840 | 790 | 580 | 700 | — | 520 |
| С3,С4, мкф | 5 | 5 | 4 | 4 | 3 | 2 | 1,5 |
| fр2,кГц | 5,8 | 5,2 | 5 | 4,4 | 4,8 | 4,6 | 5,4 |
Легко видеть, что все значения емкостей могут быть либо непосредственно взяты из номинального ряда емкостей. либо получены параллельным соединением не более чем двух конденсаторов (см. табл. 1).
После того как емкости конденсаторов выбраны, определяют индуктивности катушек в миллигенри по формулам:
В обеих формулах: Zг-в омах; fp1, fр2 — в герцах.
Поскольку полное сопротивление головки является частотнозависимой величиной, для расчета обычно принимают указанное в паспорте головки номинальное сопротивление Zг, оно соответствует минимальному значению полного сопротивления головки в диапазоне частот выше частоты основного резонанса до верхней граничной частоты рабочей полосы. При этом надо иметь в виду, что фактическое номинальное сопротивление различных образцов головок одного и того же типа может отличаться от паспортного значения на ±20%.
В некоторых случаях радиолюбителям приходится использовать в качестве высокочастотных головок имеющиеся динамические головки с номинальным сопротивлением, отличающимся от номинальных сопротивлений низкочастотной и высокочастотной головок. При этом согласование сопротивлений осуществляют, подключая высокочастотную головку В3 и конденсатор С4 к различным выводам катушки L4 (рис. 2), т. е. эта катушка фильтра играет одновременно роль согласующего автотрансформатора. Катушки можно намотать на круглых деревянных, пластмассовых или картонных каркасах с щечками из гетинакса. Нижнюю щечку следует сделать квадратной; так ее удобно крепить к основанию — гетинаксовой плате, на которой крепят конденсаторы и катушки. Плату крепят шурупами ко дну ящика громкоговорителя. Во избежание дополнительных нелинейных искажений катушки должны выполняться без сердечников из магнитных материалов.
В качестве низкочастотной головки громкоговорителя используется динамическая головка 6ГД-2, номинальное сопротивление которой Zг=8 Ом. в качестве среднечастотной — 4ГД-4 с таким же значением Zг и в качестве высокочастотной — ЗГД-15, для которой Zг=6,5 Ом. Согласно табл. 2 при Zг=8 Ом и емкости С1=С2=20 мкф fp1=700 Гц, а при емкости С3=С4=3 мкф fр2=4,8 кГц. В фильтре можно применить конденсаторы МБГО со стандартными емкостями (С3 и С4 составляют из двух конденсаторов).
По приведенным выше формулам находим: L1=L3=2,56 мГ; L2=L4=0,375 мГ (для автотрансформатора L4 — это значение индуктивности между выводами 1-3).
Коэффициент трансформации автотрансформатора
На рис. 3 показана зависимость уровня напряжения на звуковых катушках головок от частоты для трехполосной системы, соответствующей примеру расчета. Амплитудно-частотные характеристики низкочастотной, среднечастотной и высокочастотной областей фильтра обозначены соответственно НЧ, СЧ и ВЧ. На частотах раздела затухание фильтра равно 3,5 дБ (при рекомендуемом затухании 3 дБ).
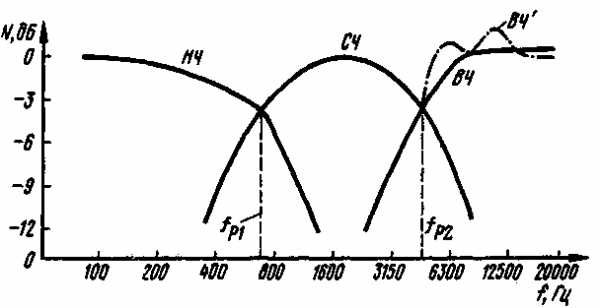
Отклонение объясняется отличием полных сопротивлений головок и емкостей конденсаторов от заданных (номинальных) значений и индуктивностей катушек от полученных расчетом. Крутизна спада кривых НЧ и СЧ составляет 9 дБ на октаву и кривой ВЧ — 11 дБ на октаву. Кривая ВЧ соответствует несогласованному включению громкоговорителя 1 ГД-3 (в точки 1-3). Как видно, в этом случае фильтр вносит дополнительные частотные искажения.
В приводимой методике расчета принято, что среднее звуковое давление при одной и той же подводимой электрической мощности для всех головок имеет примерно одинаковое значение. Вели же звуковое давление, создаваемое какой-либо головкой, заметно больше, то для выравнивания частотной характеристики громкоговорителя по звуковому давлению эту головку рекомендуется подключать к фильтру через делитель напряжения, входное сопротивление которого должно быть равно принятому при расчете номинальному сопротивлению головок.
РАДИО N 9, 1977 г., с.37-38 E. ФРОЛОВ, г. Москва
baseacoustica.ru