8-900-374-94-44
Все читатели Хабра так или иначе связаны с ИТ направлением. Будь ты программист или работаешь с железом, сетями и так далее, все мы знаем общие концепции.
Когда-то на втором курсе университета я познакомился как раз с одной из вещей, которую, по-моему, должен знать каждый из нас, ну или хотя бы услышать о ней вот в такой статье. Это стандарт представления чисел в формате с плавающей точкой(в других источниках с плавающей запятой). Как же въелось мне это название: стандарт IEEE-754.
Уверен, что каждый из айтишников хоть раз но слышал с числами в формате плавающей точкой, но для меня впервые это показалось полной чушью. И не с проста: ведь предмет, на котором мы изучали стандарт, назывался «Архитектура ЭВМ» да и преподаватель был, да и сейчас есть живой легендой. Ну, это оффтоп.
Итак, что же такое этот стандарт IEEE-754? Скажу сразу, что нам в университете дали его в электронном виде на русском, но в интернете я не смог его найти, даже дойдя до 30-й страницы гугла.
Сам стандарт представляет собой описание операций двоичной арифметики с числами в формате с плавающей точкой. Так же там описаны исключительные ситуации, возникающие в таких случаях, запись в такой формат и многое другое. Естественно, прочитав его, да ещё и с таким трудом, я не понял ничего! Ведь я совсем ничего не знал про формат с плавающей точкой. А ведь это грубо, говоря дробная часть любого числа, только точность надо знать.
По этому предмету в университете у нас рассчитывалась РГР (Расчётно-Графическая работа) и почему то тогда я понял, что стоит ей уделить больше времени, чем чему-либо и оказался прав. Это, наверное, был переломный момент моей учёбы. Я сидел ночами над этим стандартом и над конкретно поставленной передо мной задачей: «Деление двух чисел в формате с плавающей точкой двойной точности с заменой цепочек непрерывных единиц нулями и с округлением до ближайшего чётного».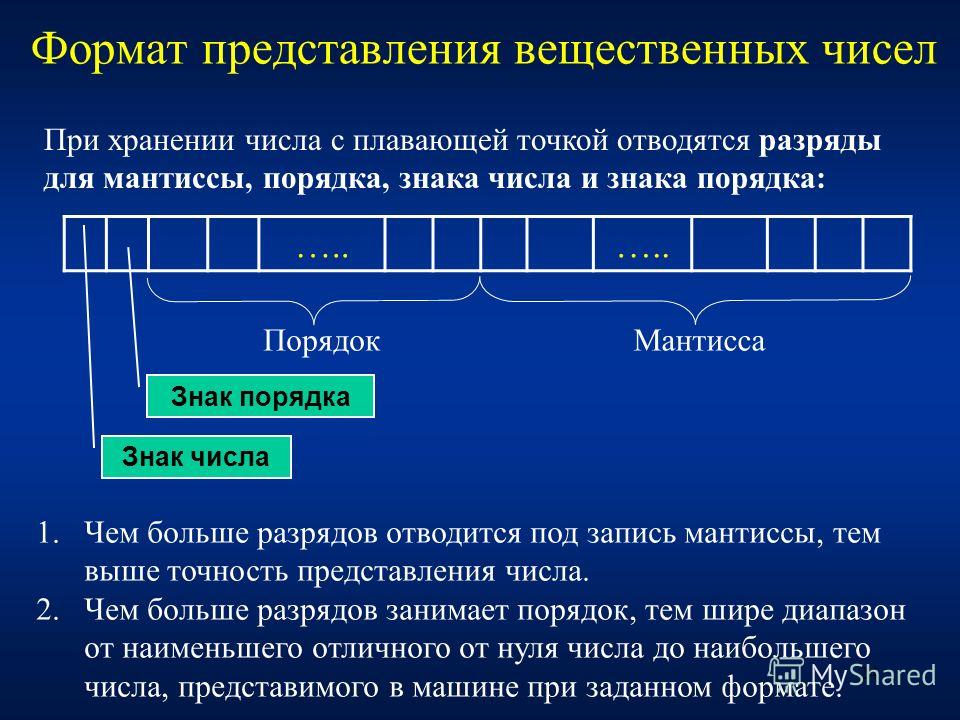
Ну, а теперь подробнее собственно, о стандарте IEEE-754. Он представляет собой несколько глав, которые я хотел бы описать поподробнее.
Всё как всегда начинается с введения. О том, что существуют программы, намного сложнее чем то, что я видел. Рассказывается об истории создания стандарта. Ведь программы становятся всё сложнее и сложнее, а ЦВМ стареет и следует заменить её новой архитектурой. Это послужило причиной тому, что IEEE (Институт инженеров по электротехнике и электронике США) в конце 70-х годов создал комиссию, рассмотревшую множество предложений. Результатом работы комиссии явился стандарт IEEE 754 ≪Двоичная арифметика с плавающей точкой≫ (1985г.), ставший международным. Его основы разработал профессор математики университета Беркли William Kahan.
— IEEE 854 – 1987, покрывающий десятичную арифметику также как и двоичную;
— IEC 60559 — 1989 IEC ≪Двоичная арифметика с плавающей точкой для
микропроцессорных систем≫ (IEC — International Electrotechnical Commission).
Стандарт IEEE 754 не обязывает, а рекомендует применение пакета оговоренных в нем форматов, способов кодирования данных, округления результатов и многое другое. Задача выбора формата для конструктора универсальной ЦВМ предельно упростилась, и с этого времени фирмы стали производить универсальные ЦВМ с арифметикой с плавающей точкой удовлетворяющей рекомендациям стандарта. Задача программистов также несколько упростилась, т.к. нет необходимости изучать особенности двоичной арифметики с плавающей точкой разных ЦВМ, достаточно овладеть знанием стандарта.
Стандарт поддерживает несколько форматов: одинарная точность(32 разряда), двойная(64 разряда) и двойная расширенная точность. Так же предусмотрены другие форматы для предотвращения ошибок округления и т.д. В стандарте описаны случаи возникновения исключительных ситуаций: Nan, бесконечность, деление на ноль и т.
д. Ничего не напоминает? Очень важную роль играет округление чисел в формате с плавающей точкой. Это тоже описано в стандарте.
И наконец-то, главный раздел – Выполнение операций над числами в формате с плавающей точкой. В этом разделе описаны все арифметические операции от сравнения до деления, а так же все нюансы при выполнении таких операций. Про этот раздел нельзя сказать вот так, «в двух словах». Скажу лишь, что это настоящая морока и передо мной встала задача понять, как это происходит.
Если операнды действительно являлись числами в формате IEEE-754, начинался второй этап выполнения операции: приведение порядков. Ни для кого не секрет, что числа в формате с плавающей точкой выглядят примерно так:
Это представление числа в формате с одинарной точностью.
Это всего лишь на словах, хоть и звучит страшно, на деле выглядит куда лучше.
Тогда я откровенно запал на этот стандарт, что принесло мне не только более глубокие знания в ЦВМ и двоичной арифметике, но и удовольствие что я смог это сделать, удовольствие осознавать то, что я знаю что-то очень важное.
У меня всё, на самом деле тема очень интересная и увлекательная. Кто заинтересовался, с удовольствием скину стандарт IEEE-754 и отвечу на ваши вопросы.
Спасибо.
Форма представления чисел с плавающей точкой предназначена для работы с вещественнымичислами, имеющими дробную часть. Так, например, число 5 — целое, а числа 5.1 и -5.0 — вещественные.
Для удобства отображения чисел,
принимающих значения из достаточно
широкого диапазона (т.е. как очень
маленьких, так и очень больших),
используется форма записи чисел с порядком основания системы счисления.
Например, десятичное число 1.
25 можно в
этой форме представить так:
1.25*100= 0.125*101= 0.0125*102= 12.5*10–1= 125.0*10–2= 1250.0*10–3= … .
Любое число Nв системе счисления с основаниемqможно записать в виде
,
где Mназываетсямантиссойчисла, аp—порядком. Такой способ записи чисел называется представлением сплавающей точкой.
Вещественные числа в ПК различных типов записываются по-разному. При этом компьютер обычно предоставляет программисту возможность выбора из нескольких числовых форматов наиболее подходящего для конкретной задачи — с использованием четырех, шести, восьми или десяти байтов.
В качестве примера в табл. 1 приведены характеристики форматов вещественных чисел, используемых IBM-совместимыми ПК.
Таблица 1. Форматы представления вещественных чисел
Форматы вещественных чисел | Размер в байтах | Примерный диапазон абсолютных значений | Количество значащих десятичных цифр |
Одинарный | 4 | 10–45 … 1038 | 7 или 8 |
Вещественный | 6 | 10–39 … 1038 | 11 или 12 |
Двойной | 8 | 10–324 … 10308 | 15 или 16 |
Расширенный | 10 | 10–4932 … 104932 | 19 или 20 |
Из таблицы видно, что форма представления
чисел с плавающей точкой позволяет
записывать числа с высокой точностью
и из весьма широкого диапазона.
При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка.
Например, число –0.125(10)= –0.001(2)= –0.1*2–10(отрицательный порядок записан в дополнительном коде) в одинарном формате представляется так:
Очевидно, что чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.
Если «плавающая» точка расположена в
мантиссе перед первой значащей цифрой,
то при фиксированном количестве разрядов,
отведённых под мантиссу, обеспечивается
запись максимального количества значащих
цифр числа, т.е. максимальная точность
представления числа в машине. Из этого
следует, что мантисса должна быть правильной дробью, первая цифра
которой отлична от нуля: 0.
1|М|<
1.
Такое, наиболее выгодное для компьютера, представление вещественных чисел называется нормализованным.
Мантиссу и порядок q-ичного числа принято записывать в системе с основаниемq, а само основание — в десятичной системе.
Примеры нормализованного представления:
Десятичная система Двоичная система
753.15 = 0.75315*103; -101.01 = -0.10101*211(порядок 11(2)= 3(10))
-0.000034 = -0.34*10-4; -0.000011 = 0.11*2-100(порядок -1002= -410)
Покажем на примерах, как записываются некоторые числа в нормализованном виде в одинарном (четырехбайтовом) формате с семью разрядами для записи порядка.
Пример 1. Число 6.2510= 110.012= 0,11001•211:
Пример 2. Число –0.12510 = –0.0012= –0.1*2–10(отрицательный порядок записан вдополнительном коде):
Задание №1
Запишите в одинарном (четырехбайтовом)
формате коды двух чисел, приведенных в
таблице №2, выбрав их в строке согласно
порядкового номера студента в журнале
учета, предварительно преобразов эти
числа в двоичную систему счисления и
нормализовав их.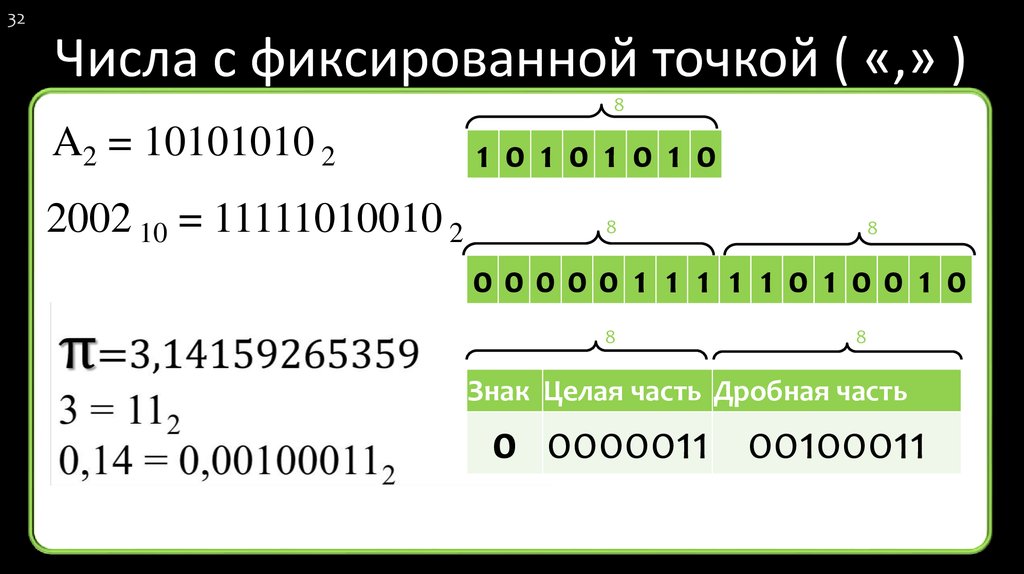
.
Таблица2
Порядковый номер | 1 | 2 |
1 | 216,329 | -4,284 |
2 | 220,541 | 1,366 |
3 | 20,526 | 6,918 |
4 | 187,757 | -0,025 |
5 | 106,700 | -6,242 |
6 | 163,885 | -4,869 |
7 | 7,485 | 7,264 |
8 | 128,277 | 4,355 |
9 | 157,767 | -7,351 |
10 | 107,001 | -0,748 |
11 | 52,404 | -2,843 |
12 | 124,936 | 6,975 |
13 | 246,541 | 0,359 |
14 | 110,766 | 6,118 |
15 | 59,096 | -7,006 |
16 | 59,281 | -4,279 |
17 | 84,722 | -2,339 |
18 | 39,178 | 6,704 |
19 | 21,215 | 4,336 |
20 | 75,458 | -0,878 |
21 | 94,466 | 2,037 |
22 | 109,968 | 5,349 |
23 | 124,992 | -3,420 |
24 | 34,691 | 8,941 |
25 | 74,391 | -0,364 |
26 | 73,443 | -0,908 |
27 | 198,007 | -1,624 |
28 | 48,844 | -2,931 |
29 | 91,843 | 5,344 |
30 | 105,141 | -0,151 |
В чем разница между инструкцией с плавающей запятой и операцией с плавающей запятой? Категория «инструкция FP» обычно включает загрузку и сохранение (например, x86 movsd xmm0, [rdi] ), копирование регистра, побитовые логические операции и другие вещи, которые не являются математическими инструкциями FP , потому что они не требует тяжелой работы по обработке знака FP/экспоненты/мантиссы или округлению и нормализации результата.
Кроме того, одна машинная инструкция может выполнять более одного FLOP (SIMD и/или FMA).
Программа, выполняющая математику FP, также будет включать некоторые целочисленные инструкции для служебных данных цикла и, возможно, для индексации массива или приращения указателя (особенно на ISA, таких как классический MIPS без режимов индексированной адресации), или если вы компилируете в режиме отладки, но вы спросили о » инструкция с плавающей запятой».
Современный конвейерный неупорядоченный ЦП будет иметь некоторое ограниченное количество исполнительных блоков FP; такие исполнительные блоки занимают много транзисторов, в отличие от скалярного целого числа , которое добавляется к , поэтому у ЦП обычно не хватает пропускной способности внутреннего исполнения FP, чтобы не отставать от внешнего интерфейса.
(например, AMD Zen имеет внешний интерфейс с 5 инструкциями / 6 операциями, но только два исполнительных модуля SIMD FP add/mul/FMA).
Некоторые рабочие нагрузки FP будут узкими местами в своей пропускной способности, выполняя достаточно мало других инструкций, поэтому пропускная способность операций FP является ограничивающим фактором, независимо от того, для какой ISA вы компилируете. (Независимо от того, разрешает ли он операнды источника памяти для FP mul, например x86, или это ISA загрузки/сохранения (например, RISC), требующая отдельных инструкций загрузки.) Пропускная способность FP, если вы можете поддерживать другие накладные расходы на инструкции достаточно низкими, чтобы ЦП фактически поддерживал свои исполнительные блоки FP работой, которую нужно выполнить.
Инструкции по загрузке и сохранению, а также такие вещи, как копирование регистров, не являются математическими операциями FP и не считаются FLOPS. Точно так же целочисленные инструкции для математики индекса массива и счетчиков циклов обычно просто накладные расходы в алгоритмах FP.
(Некоторый код FP использует разреженные массивы, компактно хранящиеся в структурах данных, которые имеют массивы целочисленных индексов или что-то еще, поэтому целочисленная работа может быть частью «реальной работы» программы в этом случае, но это все еще не математика FP).
И наоборот, SIMD выполняет несколько математических операций с помощью одной инструкции ЦП, что позволяет выполнить большой объем работы через не слишком широкий конвейер. (например, x86 vmulps ymm0, ymm1, [rdi] загружает 32 байта из памяти и выполняет 8 упакованных операций умножения одинарной точности между этими данными и элементами ymm1 .)
FMA (плавное умножение-сложение) обычно считается как два FLOP, хотя большинство процессоров, поддерживающих это, изначально делают это в одном исполнительном блоке. Так, например, Intel, начиная с Haswell, может запускать две операции SIMD FMA за такт, каждая из которых работает с 32 байтами данных (8 с плавающей запятой или 4 двойных).
Таким образом, это 2×8 FLOP с одинарной точностью за такт на ядро.
(И он имеет переднюю полосу пропускания и внутренние исполнительные блоки, чтобы также запускать две не-FMA uop, например, служебные данные цикла, сохранение результатов FMA или что-то еще, даже включая побитовое ИЛИ / И / XOR SIMD, например, для перевернуть биты знака в векторах с плавающей запятой.)
vxorps не считается FLOP, потому что это просто побитовое, а не математическое, которое должно обрабатывать мантиссу и экспоненту входных данных и нормализовать выходные данные. Перетасовка векторов SIMD также невозможна.
Вы можете считать что-то вроде x86 unpcklps xmm1, xmm0 как «инструкции с плавающей запятой» . Помимо «упакованного одиночного» в мнемонике, существует разница в производительности между целочисленными и FP-версиями одной и той же операции перемешивания или побитовой операции на некоторых процессорах. Например, Intel Nehalem имеет задержку переадресации обхода в 2 цикла, когда инструкция с плавающей точкой считывает ввод из целочисленной инструкции SIMD, такой как paddq .
См. руководство по микроархам Agner Fog, https://agner.org/optimize/, а также вопросы и ответы, такие как
por по сравнению с orps Связанный:
В последние годы задачи искусственного интеллекта, требующие больших вычислительных ресурсов, привели к созданию широкого спектра специального оборудования для эффективной работы этих новых мощных систем.
Модели глубокого обучения, такие как сверточная нейронная сеть ResNet-50, обучаются с использованием арифметики с плавающей запятой. Но поскольку операции с плавающей запятой были чрезвычайно ресурсоемкими, системы развертывания ИИ обычно полагаются на один из нескольких ставших стандартными методов целочисленного квантования с использованием математики int8/32.
Мы разработали альтернативный подход к эффективной работе моделей ИИ. Опираясь на ряд идей, восходящих к заре информатики более 70 лет назад, наш метод оптимизирует саму работу с плавающей запятой.
Мы внесли радикальные изменения в работу с плавающей запятой, чтобы сделать ее на 16 процентов более эффективной, чем int8/32 math. Наш подход по-прежнему очень точен для сверточных нейронных сетей и предлагает несколько дополнительных преимуществ:
Наши методы подробно обсуждаются в исследовательской статье «Переосмысление операций с плавающей запятой для глубокого обучения». Потребуется время, чтобы разработать новые микросхемы, предназначенные для выполнения математических операций с плавающей запятой с помощью этих методов.
Но потенциальные преимущества включают в себя более быстрые вычисления ИИ в центрах обработки данных, конструкции с меньшим энергопотреблением для лучшего ИИ на мобильных устройствах и простые и быстрые способы достижения целей производительности с меньшим количеством изменений программного обеспечения. Замедление закона Мура и эпоха «темного кремния» не за горами. Дальнейшее повышение производительности потребует переосмысления низкоуровневых решений по проектированию оборудования, принятых несколько десятилетий назад, таких как стандарт IEEE 754 с плавающей запятой, и использования математической аппроксимации там, где это применимо. Нейронные сети, в частности, предоставляют прекрасную возможность для такой переоценки, поскольку они вполне терпимы к вариациям и экспериментам.
Наши проекты оборудования для ASIC/FPGA и код C++/PyTorch для его оценки теперь общедоступны для сообщества ИИ. Мы надеемся, что сообщество ИИ присоединится к нам в изучении этого нового подхода.
Инженеры, работающие в других областях, могут быть не знакомы с тем, как традиционная операция с плавающей запятой соотносится с нашими альтернативами, поэтому краткий обзор может оказаться полезным.
Как известно, числа с плавающей запятой могут представлять как большие, так и малые действительные числа в разумном объеме компьютерной памяти, используя систему, которая в целом похожа на научную нотацию. Этот формат можно использовать для представления таких значений, как 1 000 000 и 0,0625, в кодировке фиксированной ширины и системе счисления (обычно двоичной). Важно отметить, что с плавающей запятой можно точно представить только ограниченный набор действительных чисел, поскольку у нас есть ограниченное количество битов. Все остальные значения могут быть представлены одной из нескольких форм округления до ближайшего доступного значения с плавающей запятой.
Традиционный двоичный формат с плавающей запятой имеет знак, мантиссу и показатель степени. Знаковый бит указывает, является ли число положительным или отрицательным. Мантисса (дробная часть которой обычно известна как мантисса) представляет собой двоичное число с фиксированной запятой в форме 0.bbb… или 1.bbb…, где дробная часть bbb… представлена некоторым фиксированным числом двоичных битов после системы счисления.
точка. (В десятичной арифметике точка счисления также известна как десятичная точка, отделяющая целые числа от дробных значений.) Показатель степени — это целое число со знаком, представляющее умножение мантиссы на степень 2. .bbb…) считается нормальным, а код с начальным двоичным 0 (0.bbb…) — денормальным. Стандарт IEEE 754 с плавающей запятой, распространенный в большинстве современных компьютеров, имеет как нормальные, так и денормальные значащие. Старшую цифру мантиссы не нужно явно сохранять; в IEEE 754 поле показателя степени определяет, равно ли оно 1 или 0.
На этом рисунке показано кодирование -1,625 в 16-разрядном двоичном формате IEEE 75416 с плавающей запятой половинной точности с фиксированным размером, 5-разрядным показателем степени и 10-разрядной значащей дробью. К экспоненте IEEE добавлено смещение -15, поэтому закодированная ниже экспонента 15 на самом деле представляет (15 – 15) или 0.
обучен с использованием 32-битного IEEE 754 binary32 с плавающей запятой одинарной точности.
Сокращение до 16 бит (половинная точность или форматы, такие как bfloat16) дает некоторый прирост производительности, но все равно меркнет по сравнению с эффективностью целочисленной арифметики эквивалентной разрядности. Эти варианты с плавающей запятой могут довольно легко использовать исходные 32-битные данные нейронной сети с плавающей запятой, но целочисленное квантование до 8 (или меньше) битов часто требует изучения параметров квантования и переобучения модели. Многие схемы квантования int8/32 могут работать так же точно, как исходная модель с плавающей запятой, но они также могут быть переобученными для текущей задачи, неспособной сохранить свою точность при тестировании на задачах, отличных от проверочного набора ImageNet.
Но существует множество альтернатив целочисленным, фиксированным или плавающим точкам для компьютерной арифметики, как это практикуется сегодня. Некоторые из этих методов восходят к 1950-м годам:
Мы использовали этот ряд идей для создания арифметики с плавающей запятой, которая может превзойти int8/32.
Наша реализация сильно отличается от аппаратной реализации с плавающей запятой, даже с такими вариациями, как денормализованное сбрасывание в ноль или изменения размера слова/разрядности поля, такие как bfloat16 или minifloat. В отличие от квантования int8/32, наша реализация по-прежнему представляет собой универсальную арифметику с плавающей запятой, результаты которой интерпретируются из коробки.
Чтобы разработать новый метод высокоэффективной работы с плавающей запятой, мы рассмотрели различные источники неэффективности аппаратных средств с плавающей запятой:
Чем больше точность (значащая длина) типа с плавающей запятой, тем больше будут эти компоненты. Аппаратные умножители и делители обычно гораздо более ресурсоемки (площадь чипа, мощность и задержка), чем аппаратные сумматоры.
Уменьшение размера слова обеспечивает очевидное энергетическое преимущество. Мы можем попробовать сжать 32-битные данные в 8 или 16 бит. Типичное кодирование поля фиксированного размера с плавающей запятой вынуждает делать трудный выбор для уменьшения динамического диапазона (экспонента) и точности (мантиссы), когда нам нужно некоторое сохранение обоих.
Мы можем справиться с этим компромиссом по-разному. Плавающая точка сама по себе является квантованием (бесконечной точности) действительных чисел. Квантизатор, адаптированный к распределению видимых данных, имеет меньшую ошибку воспроизведения. Обычно у нас мало предварительных знаний о распределении данных, встречающихся на компьютере общего назначения. Однако на практике распределения нейронных сетей близки к гауссовым, иногда дополнительно контролируются такими процедурами, как пакетная нормализация. Стандартная плавающая точка сохраняет такую же точность значимости при 10 ^ 5, как и при 10 ^ -5, но большинство нейронных сетей выполняют свои вычисления в относительно небольшом диапазоне, например от -10,0 до 10,0.
Часто используются крошечные числа в этом диапазоне (например, 0,0001), но не большие. В идеале мы могли бы изменить квантователь, чтобы обеспечить более высокую точность там, где это необходимо, и сохранить некоторый динамический диапазон для небольших чисел.
Коническая плавающая точка может позволить нам достичь этих целей и уменьшить размер слова. Поза Густафсона — отличная форма тейперинга. Позиции кодируют экспоненту переменным числом битов, используя код без префиксов, при этом мантистичная дробь занимает остальную часть. Он обеспечивает максимальную точность около +/- 1,0 с меньшей точностью до 0 или +/- бесконечности. Это и сжатие, и расширение с потерями, с потерей точности в некоторых местах для сохранения динамического диапазона в других местах. Таким образом, он может обеспечить как более высокую точность (в определенных местах), так и более широкий динамический диапазон, чем в случае с плавающей запятой в стиле IEEE. Позитивную идею можно распространить на другие коды без префиксов, такие как кодирование Хаффмана, когда мы заранее не знаем распределения данных.
9х имеем логарифмическую систему счисления (ЛНС), в которой умножение и деление переходят в сложение и вычитание. Однако добавление LNS требует огромных аппаратных таблиц поиска для вычисления суммы или разности двух номеров доменов журналов. Это было одной из основных проблем при внедрении LNS, поскольку эти таблицы могут быть более громоздкими, чем аппаратные множители. Обратите внимание, что типичное представление с плавающей запятой уже является комбинацией логарифмического (экспонента) и линейного (значащее) представлений, но представление LNS является полностью логарифмическим.
Полезной операцией в компьютерной линейной алгебре является умножение-сложение: вычисление суммы значения c с произведением других значений a x b для получения c + a x b . Как правило, тысячи таких продуктов могут быть суммированы в одном накопителе для такой модели, как ResNet-50, со многими миллионами независимых накоплений при запуске модели в развертывании и квадриллионами из них для обучающих моделей.
Умножение-сложение с плавающей запятой (FMA) является распространенным средством умножения-сложения с уменьшенной ошибкой, но оно намного сложнее, чем стандартный сумматор или умножитель с плавающей запятой. Метод, известный как накопление Кулиша, позволяет избежать сложности FMA. Аналогичная операция была в первом программируемом цифровом компьютере, Z3 Конрада Цузе от 1941. Густафсон также предложил стандартное использование накопления Кулиша в своих недавних исследованиях с плавающей запятой. Идея состоит не в том, чтобы накапливать в числах с плавающей запятой, а вместо этого поддерживать текущую сумму в фиксированной точке, достаточно большую, чтобы избежать недополнения или переполнения. В отличие от сложения с плавающей запятой, накопление Кулиша точно представляет сумму любого количества значений с плавающей запятой. Суммирование ассоциативно и воспроизводимо независимо от порядка. Когда мы закончим со всеми суммами, мы преобразуем их обратно в числа с плавающей запятой путем выравнивания по значимости и округления.
На приведенной ниже диаграмме показан пример этапа накопления. Аккумулятор Кулиша в настоящее время содержит значение 35,5, и мы добавляем к нему 0,84375, представленное как значение с плавающей запятой линейного домена. Это суммируемое значение с плавающей запятой могло быть получено ранее из произведения скалярных значений или просто одного значения, которое мы хотим накопить. Значение с плавающей запятой преобразуется в фиксированную за счет выравнивания точки счисления мантиссы на основе показателя степени с плавающей запятой. Это преобразование использует поправочный коэффициент, который является эффективным показателем старшего бита аккумулятора (6 в нашем примере). Затем выровненные мантиссы и аккумулятор суммируются вместе с переносом. (Для простоты мы опустили дополнительные биты точности, которые может иметь аккумулятор Кулиша для поддержки потери значимости и переполнения.) Накопление Кулиша является дорогостоящим в 32+ битах с плавающей запятой, так как накопитель, устройство сдвига и сумматор могут иметь размер более 500 бит.
, но это вполне практично для небольших типов.
Накопление по Кулишу нельзя использовать непосредственно для суммирования логарифмических доменов. Но точно так же, как накопление Кулиша выполняет сумму в форме, отличной от формы аргументов (с плавающей запятой), мы можем использовать аналогичный подход здесь, поэтому нам не нужна огромная LNS-таблица поиска суммы/разности. Мы можем аппроксимировать логарифмические значения в линейной области, Кулиш накапливать в линейной области, а затем преобразовать обратно в логарифмическую область, когда все суммы завершены. Эта стратегия очень хорошо работает для общей линейной алгебры, так как векторный скалярный продукт требует много повторяющихся сумм в аккумуляторе.
Позиционное кодирование, которое было полезно для уменьшения размера слова, также позволяет избежать этой проблемы, поскольку положительный мантисс всегда нормализован. Постепенное снижение точности предотвращает немедленное падение точности, а не постепенное, что обрабатывается в денормализованном представлении IEEE 754 путем расположения старшей единицы в мантиссе.
Позиционное сужение в сторону меньших чисел приводит к тому, что вместо этого в показателе степени используются биты значащей дроби, что расширяет динамический диапазон и снижает точность. Позитивное сужение функционально похоже на денормализованный постепенный недолив, но без накладных расходов на перенормировку мантиссы. Позитивное постепенное переполнение также поддерживается аналогичным образом при сужении.
Для повышения производительности мы комбинируем эти четыре метода. Представление логарифмической области позволяет избежать аппаратных множителей. Мы переназначаем кодировку posi для номеров журналов. Чтобы конкурировать с int8/32, мы рассматриваем 8-битный формат, называемый (8, 1, альфа, бета, гамма) log. (8, 1) — положительные параметры. Это кодирование дает соотношение более 16 миллионов к 1 между нашими наибольшими и наименьшими положительными значениями, сохраняя при этом 4 бита точности (логарифмический домен) около 1,0, все в 8 битах (всего 256 возможных значений).
Значения альфа, бета и гамма управляют точностью преобразования логарифма в линейное и линейного в логарифмическое.
Как отмечалось выше, мы выполняем суммирование в логарифмической области в линейной области. Этот результат очень приблизителен, но, в отличие от FMA, у нас нет ошибки линейной области с накоплением Кулиша для последовательных сумм. Мы называем этот метод ELMA, или точное логарифмически-линейное умножение-сложение. Умножение логарифмической области точно, как и все линейные суммы области, но логарифмическое преобразование в линейное является приблизительным, как и обратное линейное преобразование в логарифмическое. Компромисс вполне приемлем на практике.
Таблицы поиска оборудования используются для преобразования, но они намного меньше тех, которые требуются для добавления LNS. Большие параметры альфа, бета и гамма дадут более точные результаты, но также потреблят больше площади чипа и мощности.
По сравнению с FMA с плавающей запятой схема умножения-сложения ELMA по своей сути проста.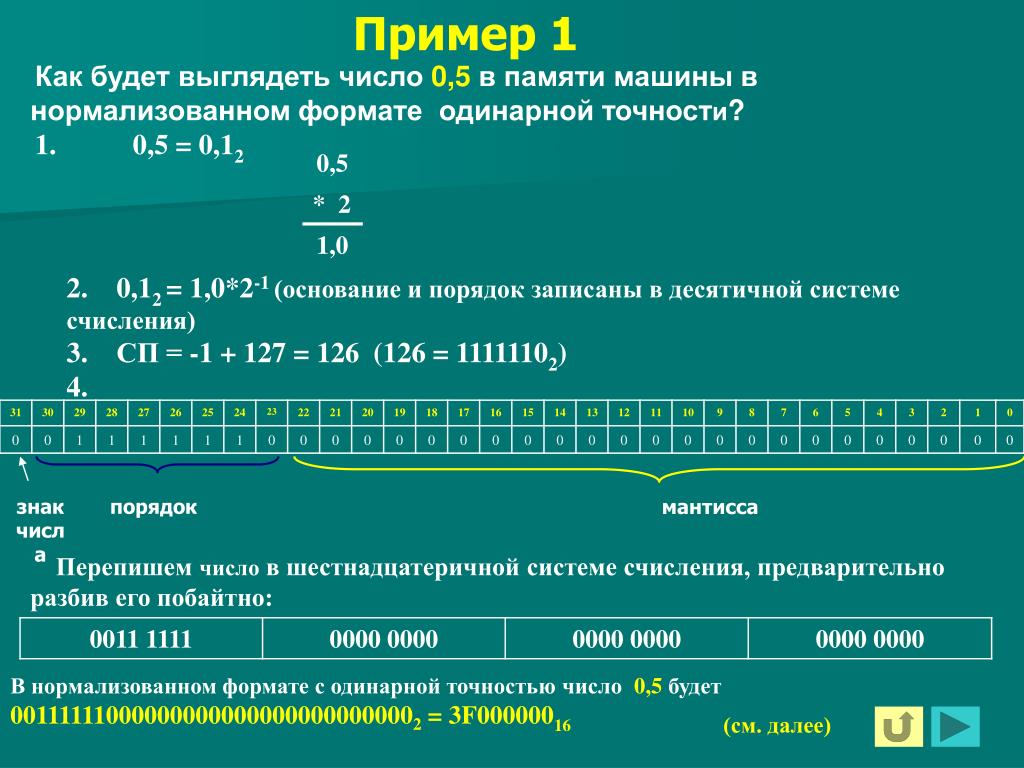
Три сумматора, интерполяционная таблица и сдвигатель выполняют большую часть работы:
В отличие от int8/32, наш 8-битный формат журнала для нейронных сетей не требует изучения параметров квантования, выборки активации, или переобучение исходной сети. Мы просто берем 32-битные параметры с плавающей запятой из сети, такой как ResNet-50, и преобразуем их с округлением до ближайшего четного. Использование кодирования posit сохраняет как необходимый динамический диапазон, так и точность в таком маленьком типе.
Используя журнал (8, 1, 5, 5, 7) с ELMA таким же образом, как и исходную математику ResNet-50, мы достигли 75,23% точности в первой и 92,66% в первой пятерке на проверочном наборе ImageNet, потеря на 0,9% и 0,2% соответственно от исходного. Эти результаты аналогичны результатам многих существующих методов квантования int8/32. Вполне возможно, что тонкая настройка обучения и настройки модели, используемые в квантовании int8/32, могут еще больше улучшить производительность нашего метода, но наш базовый результат достигается с минимальными усилиями программного обеспечения.
Вся математика по-прежнему выполняется в арифметике общего назначения с плавающей запятой, с использованием сжатого кодирования в качестве квантователя. Наш дизайн с ELMA также можно использовать для задач нелинейной алгебры, таких как вычисление полиномов.
Используя коммерчески доступный 28-нанометровый технологический процесс ASIC, мы профилировали (8, 1, 5, 5, 7) log ELMA как 0,96-кратную мощность int8/32 умножения-сложения для автономного процессорного элемента. (ЧП). В полном систолическом массиве 32×32 для матричного умножения формула log ELMA PE в 0,865 раза превышает мощность версии int8/32 PE. Экономия энергии в основном достигается за счет устранения аппаратных множителей.
Расширен до 16 бит — и даже без денормализованной поддержки, что обеспечивает большую неэффективность для IEEE 754 — этот метод использует 0,59x мощность и 0,68x площадь по сравнению с FMA половинной точности IEEE 754 с уменьшенной задержкой. Этот выигрыш в 16 битах можно использовать для поддержки обучения более сложных моделей ИИ за то же время.