

Любой квадрокоптер средней ценовой категории имеет множество режимов полета. Во всех этих режимах не всегда просто сориентироваться. Давайте попробуем разобраться как работает режим удержания высоты или Altitude Hold Mode и какие датчики за это отвечают.
Режим удержания Altitude Hold Mode позволяет пилоту управлять креном (Roll), тангажем (Pitch) и рысканьем (Yaw) не меняя высоты. Если требуется изменить высоту необходимо скорректировать положение стика газа (увеличить или уменьшить).
Умение удерживать высоту обеспечивается путем анализа давления которое измерят специальный барометрический датчик. Таким датчиком оборудовано большинство современных полетных контроллеров.
Принцип работы бародатчика основан на уменьшении атмосферного давления с увеличением высоты. Однако данные барометрического датчика не всегда точны, например, на малых высотах, в помещении или в случае перемены погоды, когда меняется давление.
Для того, чтобы повысить точность измерения на небольших высотах (до 10 метров) используются другие типы датчиков, например, ультразвуковой датчик или сонар.

Ультразвуковые сенсоры активно применяются, например, в селфи-дронах, многие из которых предназначены для полетов в помещении.
Система сенсоров дрона AirSelfie.
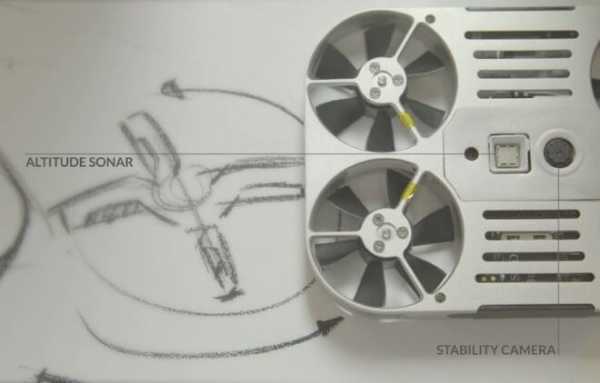
В случае с звукопоглощающими материалами ультразвуковые датчики могут неверно замерять высоту.
Еще один тип датчиков который помогает квадрокоптеру ориентироваться в пространстве — это датчик визуального позиционирования. Этот датчик активно используется в современных дронах фирмы DJI, например, Phantom 4 Pro или Mavic Pro. По сути это видеокамера, которая в режиме реального времени анализирует поверхность под дроном.
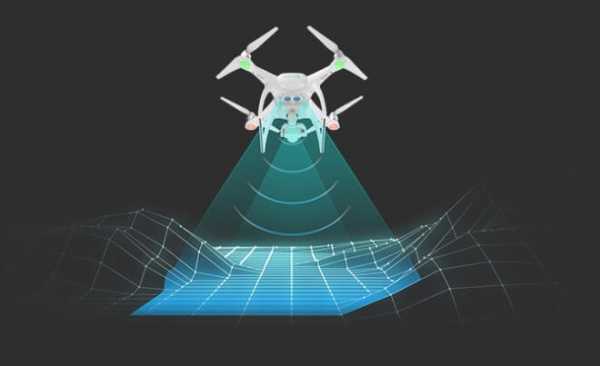
У нее тоже есть ряд ограничений, она будет некорректно работать в случае с очень темными или очень яркими поверхностями.
Если вы летаете в основном на улице, для удержания высоты используется GPS/ГЛОНАСС приемники, разумеется если они установлены на вашем дроне.
Как видите одного универсального датчика или сенсора на «все случаи жизни» не бывает, только комплекс датчиков позволяет вашему дрону ориентироваться в пространстве и корректно удерживать высоту.
Для того, чтобы вам было проще ориентироваться, мы свели всю информацию в таблицу.
| Датчик | Работает | Не работает |
|---|---|---|
| Бародатчик | На высотах более 1-2 метров | На малых высотах При плохой погоде |
| GPS | На открытом воздухе | В помещении, где поиск спутников затруднён |
| Ультразвуковой датчик | На малых высотах (до 10 метров) В помещении | На больших высотах При полетах над звукопоглощающими поверхностями При полете над наклонными поверхностями (которые отражают сигнал в сторону от дрона) |
| Датчик визуального позиционирования | В помещении и открытом воздухе На высотах (0,3 до 10 метров) | На больших высотах (свыше 10 метров) При полете над водой или прозрачными средами При полете над крайне темными или крайне яркими поверхностями При полете над одноцветной поверхностью (например, снег) При полете над поверхностями, не имеющими четких контуров или текстуры |
mirquadrocopterov.ru
Для начала немного вводной информации, чтобы прояснить, с чем предстоит иметь дело.
Мультиротор — аппарат с несколькими (3, 4, 6, 8) моторами с пропеллерами, каждый из которых создает вертикальную регулируемую тягу. В отличие от вертолета, стабилизация тут полностью электронная, и занимается ей микропроцессор при помощи ИНС (полетный контроллер).
Такой набор в сборе с Arduino-подобным процессором или в виде отдельной платки можно найти за сумму 70-100$
У каждого датчика свои возможности и слабые стороны. По отдельности ни один из них не может решить ни одну и перечисленных выше задач, поэтому системы ИНС всегда строятся из комбинации датчиков, и самое интересное тут — это вычислительные алгоритмы, позволяющие соединить сильные стороны каждого из датчиков для устранения их недостатков.
Первая задача — стабилизация ориентации — довольно успешно решается гироскопами. Гироскопы очень точно меряют угловую скорость и после интегрирования можно получить углы. Но у них есть проблема — показания уплывают со временем. Для коррекции этого дрифта применяется акселерометр, который всегда (ну или почти всегда в долгосрочной перспективе) знает, где земля. Но акселерометр ничего не почувствует, если его крутить вокруг оси Z, поэтому нам нужен магнетометр, который всегда знает, где север.
Вторая задача — нахождение высоты — частично решается барометром. Если обнулить показания на земле, то при подъеме на каждый метр мы знаем, насколько изменятся его показания (естественно, если мы не летаем 12 часов и не начала меняться погода). Но по условию задачи барометр у нас плохой, и он выдает высоту +-1м с диким шумом амплитудой примерно в этих же пределах. В реальности мой датчик показывает следующее (на 10-й секунде перемещен на 1метр):
На помощь барометру может прийти сонар, который меряет высоту с очень высокой точностью (даже тот, что я приобрел за 5$, выдает точность ± 3мм по заявлению производителя). Но сонар способен работать только невысоко над землей (2-10м), меряет долго (до 200мс), чувствителен к качеству поверхности, к углу наклона, и может терять сигнал.
Третья задача — определение координат — не решается никак указанными выше датчиками. Акселерометр в комбинации с гироскопом может выдать линейные горизонтальные ускорения, но тут есть две проблемы: постоянно действующий огромный (по сравнению с тем, что будем измерять) вектор 1G, и отсутствие привязок для коррекции. Так что определение координат остается прерогативой GPS-сенсора, и на высокую точность тут рассчитывать не приходится.
Во всех любительских полетных контроллерах задача нахождения ориентации решена хорошо и на ней останавливаться не буду. Задача довольно простая и расписана в интернете (один, два). В MultiWii используется красивое решение без сложностей типа кватернионов и матриц DCM (не забываем, что считать все это будет простенький 16-Мегагерцовый процессор), на основе упрощений для малых углов и комплементарного фильтра.
Итак, ориентацию аппарата в пространстве мы знаем с высокой степенью точности. Теперь можно перейти к основной теме статьи, т. е. постараться улучшить результаты, которые выдает барометр (или сонар), чтобы их можно было скормить ПИД-регулятору. Для этого показания должны поступать без задержек, быть точными в короткой перспективе и не сильно уплывать со временем. Тема ПИД-регуляторов заслуживает отдельного пристального изучения, так как он широко используются в системах управления процессами. Я рекомендую сначала ознакомиться с их определением, чтобы лучше понять рассуждения, изложенные ниже.
При этом влияние величины A2 на A1 пропорционально разнице между ними и определяется коэффициентом k (чем больше, тем слабее влияние).
то, регулируя величину bias, можно управлять и первым интегралом (скоростью), и вторым (смещением). Итак, цель нашего ПИД-регулятора найдена. Но надо ещё знать ошибку. Сделаем допущение, что bias зафиксируется после наступлении некоей стабилизации параметров системы (температурных, вибрационных и т. д.). Когда bias будет найден, показания акселерометра станут очень близки к истине и можно применить комплементарный фильтр, скрестив их с барометром. Величина коррекции этого фильтра и будет ошибкой, от которой будет отталкиваться ПИД-регулятор (он стремится свести ошибку к 0 за счет регулирования целевой переменной).
Дальше находим все три составляющие ПИД-регулятора. Пропорциональная (P) — это сама ошибка. Интегральная (I) — просто интегрируем её. Дифференциальная (D) — по теории надо дифференцировать ошибку. Но в ней сидят ужасные шумы барометра и акселерометра. Такое дифференцировать страшно, поэтому применим хитрость — возьмем за D-составляющую найденную акселерометром скорость с отрицательным знаком. Так как D призвана ввести затухание в регулятор, скорость тут вполне сгодится — чем она больше, тем больше надо её «погасить».
Умножим каждый из компонентов на свои коэффициенты, сложим и получим bias. Но тут применим вторую хитрость — не будем прибавлять bias напрямую к ускорению, а прибавим только I-часть. Именно она описывает величину постоянно действующей ошибки, что соответствует нашему допущению о медленном изменении bias.
P и D части прибавим к скорости, умножив на dT (так как позаимствовали их из ускорения).
Так как основная задача регулятора — найти постоянную составляющую ошибки, я решил настроить его достаточно «мягко», чтобы по минимуму влиять на кратковременные изменения. Но тут остается широкое поле для экспериментов, и все буде определяться поведением реальных датчиков.
Сделать это надо до вычитания 1G.
Теперь можно посмотреть на код и результаты.
#define ACC_BARO_CMPF 300.0f
#define ACC_BARO_P 30.0f
#define ACC_BARO_I (ACC_BARO_P * 0.001f)
#define ACC_BARO_D (ACC_BARO_P * 0.001f)
#define VEL_SCALE ((1.0f — 1.0f/ACC_BARO_CMPF)/1000000.0f)
#define ACC_SCALE 9.80665f / acc_1G / 10000.0f
err = (alt - BaroAlt)/ACC_BARO_CMPF; // P term of error
errI+= err * ACC_BARO_I; // I term of error
accZ = (accADC[0]*EstG.V.X + accADC[1]*EstG.V.Y + accADC[2]*EstG.V.Z) *
InvSqrt(fsq(EstG.V.X) + fsq(EstG.V.Y) + fsq(EstG.V.Z))
- errI - acc_1G;
// Integrator - velocity, cm/sec
vel+= (accZ - err*ACC_BARO_P - vel*ACC_BARO_D) * cycleTime * ACC_SCALE;
// Integrator - altitude, cm
alt+= vel * cycleTime * VEL_SCALE;
// Apply ACC->BARO complementary filter
alt-= err;
errPrev = err;Данные сенсоров приходят в следующих переменных:
EstG.V – вектор G (он получен ранее при нахождении ориентации)
accADC – чистые данные с акселерометра
BaroAlt – данные с барометра, конвертированные в cm
На выходе получаем accZ, vel, alt.
Как видно, вычислительная сложность алгоритма довольно простая и Arduino его «переварит» легко (особенно если перевести в целочисленную арифметику, но тогда код станет плохо читаем).
PS: в видео есть фраза об отключении алгоритма при определенном угле наклона, и и-за этого возникает выброс ошибки. На самом деле это ограничение не нужно — алгоритм работает стабильно при любом угле от 0° до 360°
Если к этому алгоритму подключить сонар (вмето BaroAlt взять SonarAlt), то кривая высоты выглядит практически идеально. Таким образом, на низкой высоте используем сонар, при появлении ошибок или близко к пределу измерений переключаемся на барометр (предварительно согласовав высоты в период поступления достоверных данных с сонара).
К сожалению, погода пока не дает провести полетные испытания нового алгоритма. Как только появятся результаты, выложу графики сонара, отлаженный исходный код всего проекта и полетное видео.
habr.com

Parrot Ar Drone 2.0
Фотография: Lee / flickr.com
Ученые из Делфтского технического университета смогли использовать единственную камеру оптического потока для определения высоты при посадке беспилотника. Статья с подробным описанием технологии опубликована в IOPscience.
Исследователи при экспериментах с квадрокоптером Parrot AR drone 2.0 обнаружили, что при посадке в автоматическом режиме беспилотник в какой-то момент начинает покачиваться. Причем амплитуда этих колебаний строго зависит от высоты. Изучив вопрос, авторы пришли к выводу, что покачивание летательного аппарата не связано с аэродинамическим влиянием небольшого расстояния до земли — причина оказалась в автоматической корректировке позиции беспилотника по камере оптического потока.
Камера оптического потока представляет собой обычную камеру, обычно закрепляемую снизу летательного аппарата, и служит для определения скорости передвижения дрона по смещению изображения. Похожим образом люди, находящиеся в движущемся автомобиле, могут определить скорость «на глаз» по смещению окружающих объектов и пейзажа.
Оказалось, что при посадке в заданной точке алгоритм при помощи камеры оптического потока отслеживает положение дрона над указанным местом и самостоятельно компенсирует смещение летательного аппарата — например, если его сдувает ветром. При этом с определенной высоты поверхность становится настолько близкой, что малейшее смещение изображения в камере оптического потока приводит к запуску непрекращающегося покачивания всего беспилотника. При этом исследователи выяснили, что амплитуда покачиваний квадрокоптера всегда привязана к конкретной высоте.
Таким образом, отмечают авторы, летательный аппарат по возникновению таких колебаний можно с достаточно высокой точностью определить высоту и высчитать удачный момент для посадки и отключения двигателей. При этом для подобного маневра нет необходимости в датчиках расстояния, альтиметре или ресурсоемкой системе распознавания препятствий — при работе управляющее программное обеспечение опирается только на данные камеры оптического потока.
Ученые полагают, что подобный метод можно использовать на серийно выпускаемых гражданских беспилотниках или в качестве запасной системы автоматической посадки на других летательных аппаратах. Кроме того, исследователи полагают, что такой подход может объяснить, как справляются с оценкой расстояний до объекта насекомые, у которых глаза расположены очень близко и не позволяют использовать полноценное стереоскопическое зрение.
Ранее исследователи из Цюрихского университета разработали прототип автономной системы стабилизации и вынужденной посадки для квадрокоптеров. Система из акселерометра, гироскопа, камеры, датчика измерения расстояния и управляющего микрочипа строит трехмерную карту поверхности под беспилотником и выбирает ровную площадку и безопасную траекторию, после чего дрон самостоятельно садится в выбранное место.
Николай Воронцов
nplus1.ru

Первый квадрокоптер героически преодолел высоту в 5 метров и вернулся на землю, став грудой обломков, продержавшись в воздухе целую минуту.
Следующие модели летали дальше, выше и дольше. Мечта, о личном высотном рекорде, разгоралась в душе все сильнее и сильнее.
Для полета в высоту, аппарат должен летать как можно дольше. Минимум 20 минут, этого времени достаточно, чтобы подняться на высоту в 1км, спуститься, и иметь запас «топлива в баках» на непредвиденные ситуации. Решено не использовать бустеры, мощные передатчики, громоздкие антенны, все элементы должны быть штатными.
После первого облета, заменил пропеллеры на carbon 13×4.0 (пришлось немного удлинить лучи). Это позволило увеличить время полета с 20 до 28 минут.

Для оценки ситуации, поведения аккумуляторов в минусовую температуру, первый полет был на высоте 600 метров.
Несмотря на все удачные тесты, финальный полет проходил в легком мандраже. Время подъема 9 минут, зафиксировали рекорд и бегом назад. Спускаться на коптере всегда дольше чем подниматься, нельзя допустить «раскачки».

Антенна принимающая видеосигнал должна быть очень хорошая, частенько пропадал сигнал, хотя в очки Fatshark сигнал принимался практически без помех.
Аккумуляторы, при отрицательных температурах, утеплять обязательно, т.к. при спуске, нагрузка на них уменьшается и они «мерзнут» теряя при этом свою емкость.
Особое внимание уделить технике безопасности — при failsave контроллер Naza возвращается домой, если коптер находится на значительной высоте над головой, сигнал аппаратуры теряется полностью.
Спускаться с высоты лучше по спирали, коптер ведет себя намного стабильнее.
Гоупро лучше ставить в режим фото, картинка должна получиться интереснее чем с видео.





habr.com

Основная задача квадрокоптера — передвигаться по воздуху на определенное расстояние и выполнять специальные действия. В основном квадрокоптеры используют для съемки видео и любительских целей, поэтому различают самые разные модели по стоимости и характеристикам.
Если вы владеете квадрокоптером, то часто задавались вопросом по поводу максимальной высоты полета, ведь чем дороже и качественнее устройство, тем лучше у него передатчик для полетов.
Разумеется, что летать в другие города на такой технике практически невозможно, но мощные устройства могут передвигаться на несколько километров с профессиональной съемкой видео высокого формата.
Стоит отметить, что помимо характеристик и свойств датчика нужно уметь правильно выполнять манипуляции с пультом управления.
Ведь для достижения максимальной высоты подъема квадрокоптера нужно постоянно жать джойстик на пульте в положении вверх. И когда высота перестанет набираться, это и будет свидетельствовать о пиковой точке.
На высоту подъема влияют следующие факторы:
Дешевые «бытовые» устройства имеют не только простое программное обеспечение и слабый двигатель, в самых простых моделях сигнал передается посредством Bluetooth, который в отличие от WI-FI передает связь всего на 20-30 метров.
Что касается надежных профессиональных устройств, то датчик высоты квадрокоптера позволит подняться на высоту 1,5-2 км.
Простой пример: квадрокоптер DJI Phantom 4 может подниматься на максимальную высоту 6 км, тогда как профессиональная промышленная модель AEE F100 Drone может достичь высоты целых 10 км.

Учтите, что характеристики максимальной высоты нельзя отрегулировать, как и стандартную емкость аккумулятора. Единственное, вы можете заменить текущую батарею на более производительную для более длительного использования. Но в таком случае будьте внимательны, ведь входное и выходное напряжение должно быть идентичным старому аккумулятору. В противном случае ждите поломки всего квадрокоптера.
Некоторые умельцы заменяют штатные двигатели на более мощные, но при наличии сервисного обслуживания вы потеряете все привилегии, даваемые производителем.
Разумеется, если вы используете любительские дешевые дроны, надеяться на отличные характеристики высоты попросту не стоит. Миниатюрные дроны работают на высоте до 20-50 метров, поэтому их применяют либо в закрытых помещениях, либо на улице без ветра.
Что касается бюджетных моделей для любительского или полупрофессионального использования, их радиус действия будет зависеть от радиочастот. Следовательно, выбирают максимальные показатели мощности приемника и передатчика.
Несмотря на свою «бюджетность», такое устройство способно выдать максимальную высоту 100-150 метров. Для набора подобной высоты на двигатели коптеров устанавливают контроллеры, не дающие превысить допустимые обороты двигателя.
Профессиональные модели для аэросъемки используют аккумулятор большой емкости, позволяющий достичь высоты полета около 1 000 метров.

Если квадрокоптер не держит высоту, причин может быть несколько. Зачастую это проблемы с двигателями или качеством сигнала, но помочь смогут лишь профессионалы в данной области.
Если интересно, на какую высоту взлетает квадрокоптер, ознакомьтесь с парой примеров:
[veo class=”veo-yt” string=”Qi0LSMN9_ME”]
geekhard.ru
В прошлой статье мы вплотную приблизились к построению простой БИНС на основе гироскопа, акселерометра и цифрового компаса. Давайте продолжим.
В данной статье мы рассмотрим одни из самых простых вариантов — комплементарный фильтр. В разных источниках данный алгоритм называют по разному (комплементарный фильтр, композитный фильтр, альфа-бета фильтр). Но идея одна, данный фильтр представляет собой комбинацию фильтра низкой частоты и фильтра высокой частоты.
Сразу напрашивается вопрос: почему мы говори о цифровых фильтрах, ели мы строим БИНС? Просто, в данной реализации, для определения положения (углов), используется именно алгоритм фильтра. По мере углубления в материал все станет понятно.
Как уже было сказано, данный алгоритм – один из самых простых, но он успешно используется в в платах управления коптерами. Насколько он эффективен – лучше спросить у владельцев платы управления на базе MultiWii, в которой используется этот алгоритм. Судя по отзывам на форумах – плата весьма неплохо себя зарекомендовала.
Перейдем к делу, и рассмотрим сначала «одномерный» случай, а потом перейдем к трехмерному пространству.
Пока предположим, что наш ЛА неподвижен. У нас есть 2 значения одного и того же угла. Одно значение (Ag) мы получили интегрируя показания с гироскопа, второе (Aa) на основании показаний акселерометра. На всякий случай напомню, что в случае неподвижного ЛА, акселерометр нам даст вектор, направленный вертикально вверх, и этот вектор мы хотим использовать для коррекции накапливающейся погрешности.
Собственно говоря, для введения кориектировки мы будем после каждого цикла интегрирования «смешивать» показания с гироскопа (после интегрирования) и акселерометра в определенной «пропорции». Пропорция будет определяться «весами» w1 и w2 соответственно.
A = (w1 *Ag + w2 *Aa ) / (w1 + w2)
где:
A – значение скорректированного угла
Ag – значение угла «по гироскопу» (результат интегрирования)
Aa – значение угла «по акселерометру»
w1, w2 – «веса»
Вот, собственно, данное выражение и есть наш фильтр. Давайте попробуем «на пальцах» разобраться, как это работает. Для наглядности перейдем к частному случаю, приняв, что w1 = (1 – w2), а w2 обозначим как w, причем w лежит в диапазоне {0… 1}. Получим:
A = (1 – w) *Ag + w *Aa
В данном случае w – это единственный параметр фильтра, значение которого нам нужно будет подобрать/вычислить.
Чтобы наглядно продемонстрировать работу фильтра, давайте проделаем мысленный эксперимент. Предположим ЛА неподвижен, при этом Aa = 4 (что соответствует реальному значению угла) а Ag = 3 (отличается от реального значения из-за накопившейся погрешности при интегрировании). Примем значение параметра фильтра w=0.1 и посмотрим, как будет меняться значение скорректированного угла в каждой итерации цикла интегрирования (цикле опроса датчиков).
0. (1 - 0.1) * 3.00 + 0.1 * 4.00 = 3.10
1. (1 - 0.1) * 3.10 + 0.1 * 4.00 = 3.19
2. (1 - 0.1) * 3.19 + 0.1 * 4.00 = 3.27
3. (1 - 0.1) * 3.27 + 0.1 * 4.00 = 3.34
4. (1 - 0.1) * 3.34 + 0.1 * 4.00 = 3.41
5. (1 - 0.1) * 3.41 + 0.1 * 4.00 = 3.47
...
22. (1 - 0.1) * 3.90 + 0.1 * 4.00 = 3.91
23. (1 - 0.1) * 3.91 + 0.1 * 4.00 = 3.92
24. (1 - 0.1) * 3.92 + 0.1 * 4.00 = 3.93
...
n. (1 - 0.1) * 4.00 + 0.1 * 4.00 = 4.00
Я извиняюсь за такую излишне «разжеванную» подачу материала, просто хотелось все продемонстрировать «на пальцах».
Из такой «симуляции» видно, что с каждой итерацией цикла значение скорректированного угла (A) стремится к реальному значению угла (4).
Наш алгоритм корректировки, в принципе, работает. Чем больше будет коэффициент w – тем быстрее будет происходить корректировка.
Но пока мы «работали» с неподвижной моделью. Если ЛА начнет ускорятся, то наш «эталонный» угол (Aa), полученный с акселерометра, будет отклонятся. Что произойдет тогда?
Вот здесь, наш фильтр и проявляет себя как фильтр. Если посмотреть на правую часть выражения A = (1 – w) *Ag + w *Aa, то при малых значениях w произведение w *Aa работает как фильтр низких частот для Aa.
Другими словами, из-за малого значения коэффициента w существенное изменение Aa не приводит к резкому и существенному изменению значения скорректированного угла A. Если в процессе работы нашего цикла интегрирования значение Aa кратковременно (пусть даже значительно) отклонится – мы этого практически не заметим. Значение скорректированного угла А будет сремится к усредненному значению Aa. Чем меньше коэффициент w тем больше будет «усредняется» значение Aa.
Если вынуться к коптреам, то наш фильтр будет подавлять кратковременные отклонения «эталонного» вектора, вызванные собственным ускорением коптера. Конечно, если ускорение будет действовать достаточно долго (и направлено в одну сторону), то усредненное значение вектора существенно сместиться от вертикали. В этом случае, наш фильтр будет не корректировать, а, наоборот, вносить погрешность.
Но, на практике данный подход успешно работает для «среднестатистического» режима полета квадрокоптера. Плюс, не забавам, что есть пилот, который управляет полетом и может вмешаться. И не забываем, что это одна из самых простых реализаций БИНС. Дальше будут более «интеллектуальные» системы.
Теперь рассмотрим, как это все работает в реальной жизни (в трехмерном пространстве) на примере прошивки MultiWii v1.9. Данная прошивка реализует «абсолютную» стабилизацию коптера по углам крена и тангажа. Для определения углов используется гироскоп, для коррекции ошибки – акселерометр или цифрой компас.
Для начала, нужно перейти от одномерной системы к трехмерной. Есть несколько способов, большинство склоняются к использованию кватерионов. В данной прошивке оперируют векторами в декартовой системе координат и матрицами поворота, чем воспользуемся и мы.
Для описания гулов крена и тангажа воспользуемся вектором – нормалью к горизонтальной плоскости (R). При инициализации программы, когда ЛА стоит на земле, мы явно присваиваем значения проекциям данного вектора Rх = 0, Ry = 0, Rz = 1. Получаем вектор, который направлен вертикально вверх, и совпадает по направлению с вектором, получаемым с акселерометра (G).
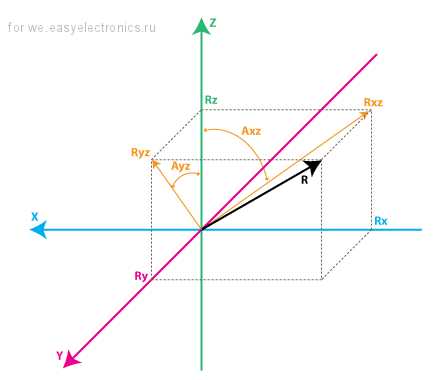
Теперь рассмотрим основной цикл управления.
1. Получаем моментальные значения углов с гироскопа, умножаем их на значение времени между опросами (разница между текущим значением времени и временем предыдущего опроса гироскопа — t). Для каждого из углов получаем приращение угла (значение угловой скорости * t).
2. Используя матрицу поворота, поворачиваем вектор R на значения углов приращения в противополженную строну. Это, в данном случае, и есть интегрирование. Полученный вектор R определят расчетное положение коптера относительно горизонта.
3. Получаем моментальное значение проекций вектора G с акселерометра.
4. Используя проекции вектора R и вектора G корректируем значение вектора R:
Rx = (1 — w) * Rх + w * Gx
Rу = (1 — w) * Rу + w * Gy
Rz = (1 — w) * Rz + w * Gz
5. Нормализируем вектор R (приводим значение вектора по модулю к 1).
6. Используем полученное значение вектора R для определения отклонения от горизонтального положения, отклонение подаем на ПИД регулятор.
7. Переходим к пункту 1.
Вот, приблизительно как-то так.
Есть несколько особенностей в реализации MultiWii, на которые хотелось бы обратить внимание.
1. Для матрицы поворота используются аппроксимация для малых углов. Считается, что приращение угла за один период цикла будет очень небольшим, и для таких углов считаем что sin(x) = x, cos(x) = 1
2. Корректировка угла (пункт 4) выполняется только в том случае, если значение вектора G по модулю приблизительно равно g.
Что почитать:
1. Обзорная статья (вернее стенограмма доклада)
2. Неплохая статья на английском.
3. Исходники MultiWii (код, честно говоря, написан плохо).
Заранее приношу извинения за возможные неточности. Исправления и уточнения приветствуются.
we.easyelectronics.ru

Здравствуйте, хаброжители!
В этой серии статей мы с вами приоткроем крышку квадрокоптера чуть больше, чем этого требует хобби, а также напишем, настроим и запустим в воздух собственную программу для полетного контроллера, которым будет являться обычная плата Arduino Mega 2560.
У нас впереди:
Без ущерба для понимания в базовых понятиях смело пропускайте все, что вам известно, до следующего незнакомого термина, выделенного жирным, или до непонятной иллюстрации.
Не беритесь писать собственную программу для полетного контроллера, пока не попробуете готовые решения, которых сейчас достаточно много (Ardupilot, MegapirateNG, MiltiWii, AeroQuad и т.п.). Во-первых, это опасно! Чтобы управлять квадрокоптером без GPS и барометра нужна практика, а тем более, когда он глючит, переворачивается, летит не совсем туда, куда надо — а этого почти не избежать во время первых тестов. Во-вторых, вам будет во много раз легче программировать понимая, что нужно программировать и как оно должно работать в итоге. Поверьте: математика полета — лишь малая часть кода программы.Не беритесь писать собственную программу для полетного контроллера, если вас не преследует академический интерес и вам нужно только то, что уже давно умеют готовые решения (летать, фотографировать, снимать видео, летать по заданию и т.п.) Пока вы сами все напишите, пройдет немало времени, даже если вы не один.Мы будем летать на раме квадрокоптера формы «X», потому что она мне больше нравится внешне. У каждой конструкции свои плюсы и свое предназначение. Кроме квадрокоптеров есть и другие мультикоптеры. Даже если не считать экзотические варианты, все равно их видов — целая куча!
Разберемся, как наш квадрокоптер устроен внутри, и чем же должен заниматься полетный контроллер, который мы планируем программировать.
Углы тангажа, крена и рыскания (pitch, roll, yaw) — углы, которыми принято определять и задавать ориентацию квадрокоптера в пространстве.
Иногда слово «угол» опускают и просто говорят: тангаж, крен, рыскание. Но согласно Википедии это не совсем точно. Полет квадрокоптера в необходимом направлении достигается изменением этих трех углов. Например, чтобы полететь вперед квадрокоптер должен наклониться за счет того, что задние моторы закрутятся чуть сильнее передних:
Газ квадрокоптера — среднее арифметическое между скоростями вращения всех моторов. Чем больше газ, тем больше суммарная тяга моторов, тем сильнее они тащат квадрокоптер вверх (НЕ ВПЕРЕД!!! «Тапок в пол» здесь означает наискорейший подъем). Обычно измеряется в процентах: 0% — моторы остановлены, 100% — вращаются с максимальной скоростью. Газ висения — минимальный уровень газа, который необходим, чтобы квадрокоптер не терял высоту.
Газ, тангаж, крен, рыскание — если вы можете управлять этими четырьмя параметрами, значит вы можете управлять квадрокоптером. Их еще иногда называют каналами управления. Если вы приобрели двухканальный пульт, с квадрокоптером вам не совладать. Трехканальный скорее подойдет для маленьких вертолетов: без управления креном летать можно, но на квадрокоптере — не удобно. Если вы хотите менять режимы полета, придется раскошелиться на пятиканальный пульт. Хотите управлять наклоном и поворотом камеры на борту — еще плюс два канала, хотя профессионалы используют для этого отдельный пульт.
Режимов полета существует много. Используется и GPS, и барометр, и дальномер. Но мы хотим реализовать базовый — режим стабилизации (stab, stabilize, летать в «стабе»), в котором квадрокоптер держит те углы, которые ему задаются с пульта не зависимо от внешних факторов. В этом режиме при отсутствии ветра квадрокоптер может висеть почти на месте. Ветер же придется компенсировать пилоту.
Направление вращения винтов выбирается не случайно. Если бы все моторы вращались в одну сторону, квадрокоптер вращался бы в противоположную из-за создаваемых моментов. Поэтому одна пара противостоящих моторов всегда вращается в одну сторону, а другая пара — в другую. Эффект возникновения моментов вращения используется, чтобы изменять угол рыскания: одна пара моторов начинает вращаться чуть быстрее другой, и вот уже квадрокоптер медленно поворачивается к нам лицом (ужас какой):
Обобщенной задачей полетного контроллера является несколько десятков раз в секунду выполнять цикл управления в который входит: считывание показаний датчиков, считывание каналов управления, обработка информации и выдача управляющих сигналов моторам, чтобы выполнять команды пилота. Именно это мы и собираемся запрограммировать.
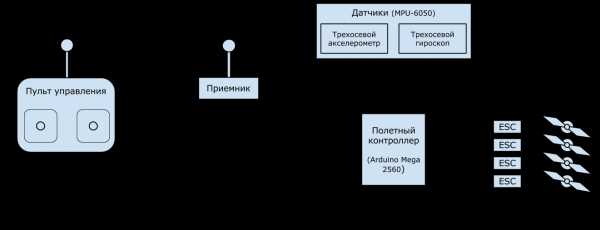
Различных видов датчиков, которые можно задействовать, очень много. Мы будем использовать ставшие уже почти обязательными во всех квадрокоптерах трехосевой гироскоп и трехосевой акселерометр. Акселлерометр измеряет ускорение, гироскоп измеряет угловую скорость. Благодаря им полетный контроллер узнает текущие углы тангажа, крена и рыскания. Эти датчики бывают встроенными в полетный контроллер, а бывают внешними. Процесс вычисления трех углов по показаниям датчиков — тема для отдельной статьи. Но нам этого здесь знать не надо: за нас все сделает MPU-6050. Это небольшая плата, проводящая необходимые вычисления и фильтрации у себя внутри и выдающая по протоколу i2c уже почти готовые углы. Нам останется их считать, обработать с остальными данными и выдать управляющие сигналы моторам.
Моторы на мультикоптерах потребляют большие токи, поэтому полетный контроллер управляет ими не напрямую, а через специальные аппаратные драйвера, называемые регуляторами скорости (ESC, ре́гуль, е́ска). Эти регуляторы питаются от основного бортового аккумулятора, управляющий сигнал получают от контроллера, а на выходе у них стоит по три провода (A, B, C), которые непосредственно идут к моторам (каждому мотору — свой регуль!)
«Протокол» общения между регулятором и мотором нам не так важен, как «протокол» общения между полетным контроллером и регулятором, ведь нам предстоит из контроллера программно управлять регулятором. Бывают регуляторы, управляемые по i2c, но наиболее распространенные управляются сигналом прямоугольной формы с минимумом 0 вольт и максимумом 3-5 вольт (его называют ШИМ или PWM, а некоторые утверждают, что правильнее — PPM. Подробнее, например, здесь).
«Протокол» — это громко сказано: чтобы дать команду мотору вращаться с максимальной скоростью контроллер должен отправлять импульсы длительностью 2 миллисекунды, перемежающиеся логическим нулем длительностью 10 — 20 миллисекунд. Длительности импульса в 1 миллисекунду соответствует остановка мотора, 1.1 мс — 10% от максимальной скорости, 1.2 мс — 20% и т.п. Практически длительность нуля не играет никакой роли, важна только длительность самого импульса.
При всей кажущейся простоте, здесь кроется засада: полетные контроллеры бывают разные с разными настройками, регуляторы бывают разные, и минимум (1 мс) и максимум (2 мс) — не универсальны. В зависимости от множества факторов диапазон 1-2 мс может на деле оказаться 1.1 — 1.9 мс. Для того, чтобы регулятор и контроллер говорили абсолютно на одном языке существует процедура калибровки регуляторов. В ходе этой процедуры диапазоны регуляторов изменяются и становятся равными диапазону контроллера. Процедура зашита в программу каждого регулятора и включает в себя несколько простых шагов (шаги могут отличаться в зависимости от производителя — читайте инструкции!):
PWM с точно таким же принципом использует и бортовой приемник. Это небольшое устройство, получающая сигналы радиоуправления с земли и передающая их в полетный контроллер. Чаще всего в полетном контроллере для каждого канала управления (газ, тангаж, крен и т.п.) имеется свой вход на который поступает PWM. Логика взаимодействия проста: команда, например, «70% газ» непрерывно идет с земли на приемник, где преобразуется в PWM и по отдельному проводу поступает в полетный контроллер. Аналогично с тангажем, креном, рысканием.
Раз между приемником и контроллером свои товарищеские PWM отношения, то их тоже придется калибровать: пульты с приемниками бывают разные со своими диапазонами работы. Контроллер должен уметь подстраиваться. Процедуру калибровки радио, в отличие от калибровки регуляторов нам придется создавать самим как часть полетный программы. Общий план калибровки такой:
Помимо программы для полетного контроллера необходима еще одна программа: интерфейс настройки полетного контроллера. Чаще всего им является программа для PC, которая соединяется с полетным контроллером по USB и позволяет пользователю настраивать и проверять полетную программу, например: запускать калибровку радио, настраивать параметры стабилизации, проверять работу датчиков, задавать маршрут полета на карте, определять поведение мультикоптера при потере сигнала и многое другое. Мы свой интерфейс настройки будем писать на C++ и Qt в виде консольной утилиты. Вот она, если заглянуть в будущее:
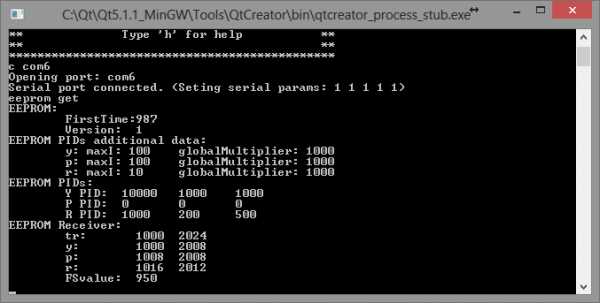
Никто не застрахован от случайностей. Даже десятидюймовые пластиковые винты на маленьких моторах могут оставить кровавые синяки на коже, которые будут болеть еще неделю (проверено лично). Элементарно сделать себе новый макияж и прическу, если зацепить стик газа на пульте, пока несешь включенный квадрокоптер. Поэтому полетный контроллер должен обеспечивать хоть какую-то безопасность: механизм armed/disarmed. Состояние квадрокоптера «disarmed» означает, что моторы отключены и даже команда полного газа с пульта не имеет никакого эффекта, хотя питание подано. Состояние «armed» квадрокоптера означает, что команды с пульта выполняются полетным контроллером. В этом состоянии квадрокоптеры взлетают, летают и садятся. Квадрокоптер включается и должен сразу попасть в состояние disarmed на тот случай, если невнимальельный пилот включает его, когда стик газа на пульте находится не в нуле. Чтобы перевести коптер в состояние «armed» пилоту необхоимо сделать какой-то заранее оговоренный жест стиками пульта. Часто этим жестом является удержание левого стика в правом нижнем углу (газ = 0%, рыскание = 100%) втечении пары секунд. После этого полетный контроллер делает хотя бы минимальную самопроверку и при ее успешном прохождении «армится» (к полету готов!) Другим жестом (газ = 0%, рыскание = 0%) квадрокоптер «дизармится«. Еще одна хорошая мера безопасности — автодизарм, если газ был на нуле втечении 2-3 секунд.
О моторах, аккумуляторах, регуляторах, пропеллерахВыбор комплектующих для мультикоптера — тема для целого цикла статей. Если вы собираетесь сделать свой первый квадрокоптер — сформулируйте, для чего он вам нужен, и воспользуйтесь советами бывалых или возьмите список комплектующих, который составил кто-то другой и успешно на нем летает.И все же для общего понимания полезно знать основные моменты.
Каждая банка является отдельным аккумулятором. Все они спаяны последовательно. Для того чтобы равномерно заряжать все банки предусматривается баллансировочный разъем с доступом к каждой банке отдельно, и использутся специальные зарядные устройства.
Если мотор рассчитан на ток до 30А, то регулятор стоит рассчитывать на ток до 30 + 10А, чтобы не допускать перегревов. Некачественные или неподходящие регуляторы могут вызвать так называемые «срывы синхронизации» и остановку мотора в полете, и вы узнаете еще один мультироторный термин: «поймал планету.» Еще один важный момент — толщина и качество проводов. Неправильно рассчитанное сечение провода или плохой коннектор могут привести к пожару в воздухе.
Как видите, нюансов очень много. Я не перечислил даже половины, поэтому самому подобрать комплектующие для первого мультикоптера довольно трудно.
Вы приобретаете двухосевой подвес для камеры, ставите туда, например, GoPro, включаете и вместо стабилизации получаете конвульсии, вибрации и дергания, хотя все датчики откалиброваны и механические проблемы устранены. Причина — неверные параметры ПИД-регуляторов.
Вы собираете мультикоптер, калибруете датчики, регуляторы, радио, все проверяете, пытаетесь взлететь, а он такой унылый в воздухе, что его даже легким ветерком переворачивает. Или наоборот: он такой резкий, что внезапно срывается с места и крутит тройное сальто без разрешения. Причина все та же: параметры ПИД-регуляторов.
Для многих устройств использующих ПИД-регуляторы существуют инструкции по настройке, а то и несколько в добавок к многочисленным видеонструкциям от самих пользователей. Но чтобы легче ориентироваться в этом многообразии полезно понимать, как же внутри устроены эти регуляторы. Кроме того, мы же собираемся писать собственную систему стабилизации квадрокоптера! Предлагаю вместе со мной самим заново «изобрести» и «на пальцах» понять формулу ПИД-регулятора. Для тех, кому больше нравится сухой математический язык, я рекомендую Википедию, английскую статью, т.к. в русской пока не так подробно изложен материал.
Будем рассматривать квадрокоптер в двумерном пространстве, где у него есть только один угол — угол крена, и два мотора: левый и правый.
В полетный контроллер непрерывно поступают команды с земли: «крен 30 градусов», «крен -10 градусов», «крен 0 градусов (держать горизонт)»; его задача — как можно быстрее и точнее их выполнять с помощью моторов с учетом: ветра, неравномерного распределения веса квадрокоптера, неравномерного износа моторов, инерции квадрокоптера и т.п. Таким образом, полетный контроллер должен непрерывно решать задачу, какую скорость вращения подавать на каждый мотор с учетом текущего значения угла крена и требуемого. Непрерывно — это, конечно, громко сказано. Все зависит от вычислительных возможностей конкретного железа. На Adruino вполне можно одну итерацию цикла обработки и управления уместить в 10 миллисекунд. Это значит, что раз в 10 миллисекунд будут считываться показания углов квадрокоптера, и на их основе будут отправляться управляющие сигналы к моторам. Эти 10 миллисекунд называют периодом регулирования. Понятно, что чем он меньше, тем чаще и точнее происходит регулирование.
Уровень газа поступает из приемника в контроллер. Обозначим его . Напомню, что это среднее арифметическое между скоростями вращения всех моторов, выраженное в процентах от максимальной скорости вращения. Если и — скорости вращения левого и правого моторов, то:
где — реакция квадрокоптера (усилие), которое создает момент вращения за счет того, что левый мотор вращается на быстрее, чем газ, а правый — на столько же медленнее. может принимать и отрицательные значения, тогда правый мотор закрутится быстрее. Если мы научимся вычислять эту величину на каждой итерации цикла обработки, значит мы сможем управлять квадрокоптером. Понятно, что как минимум должно зависеть от текущего угла крена () и желаемого угла крена (), который поступает с пульта управления.
Представим ситуацию: поступает команда «держать горизонт» ( = 0), а квадрокоптер имеет крен влево:
— разность (ошибка) между и , которую контроллер стремится минимизировать.
Чем больше разность между желаемым углом крена и текущим, тем сильнее должна быть реакция, тем быстрее левый мотор должен закрутиться относительно правого. Если это записать с использованием наших обозначений:
Здесь P — коэффициент пропорциональности. Чем он больше, тем сильнее будет реакция, тем резче квадрокоптер будет реагировать на отклонение от требуемого угла крена. Эта интуитивно понятная и простая формула описывает работу пропорционального регулятора. Суть элементарна: чем сильнее квадрокоптер отклонился от требуемого положения, тем сильнее надо пытаться его вернуть. К сожалению, эту формулу придется усложнить. Главная причина — перерегулирование.
За несколько десятков миллисекунд (несколько итераций цикла обработки) под воздействием пропорционального регулятора квадрокоптер вернется в требуемое (в данном случае горизонтальное) положение. Все это время ошибка и усилие будут иметь один и тот же знак, хоть и становиться все меньше по модулю. Набрав какую-то скорость поворота (угловую скорость) квадрокоптер просто перевалится на другой бок, ведь никто его не остановит в требуемом положении. Все равно что пружина, которая всегда стремится вернуться в начальное положение, но если ее оттянуть и отпустить — будет колебаться, пока трение не возьмет верх. Конечно, на квадрокоптер тоже будет действовать трение, но практика показывает, что его не достаточно.
По этой причине в пропорциональный регулятор нужно добавить еще одно слагаемое, которое будет тормозить вращение квадрокоптера и препятствовать перерегулированию (переваливанию в противоположную сторону) — своего рода имитация трения в вязкой среде: чем быстрее поворачивается квадрокоптер, тем сильнее надо пытаться его остановить, конечно, в разумных пределах. Скорость вращения (скорость изменения ошибки ) обозначим как , тогда:
где D — настраиваемый коэффициент: чем он больше, тем сильнее останавливающее усилие. Из школьного курса физики всплывают смутные воспоминания, что скорость изменения любой величины — производная этой величины по времени:
.
И вот пропорциональный регулятор превращается в пропорционально-дифференциальный (пропорциональное слагаемое и дифференциальное):
.
Ошибку вычислить легко, ведь на каждой итерации мы знаем и ; P и D — настраиваемые перед запуском параметры. Для вычисления производной (скорости изменения ) необходимо хранить предыдущее значение, знать текущее значение и знать время, которое прошло между измерениями (период регулирования). И вот она — физика шестого класса школы (скорость = расстояние / время):
.
— период регулирования; — значение ошибки с предыдущей итерации цикла регуляции. Кстати, эта формула — простейший способ численного дифференцирования, и он нам здесь вполне подойдет.
Теперь у нас есть пропорционально-дифференциальный регулятор в плоском «бикоптере», но осталась еще одна проблема. Пусть левый край будет весить чуть больше правого, или, что то же самое, левый мотор работает чуть хуже правого. Квадрокоптер чуть наклонен влево и не поворачивается обратно: дифференциальное слагаемое равно нулю, а пропорциональное слагаемое хоть и принимает положительное значение, но его не хватает, чтобы вернуть квадрокоптер в горизонтальное положение, ведь левый край весит чуть больше правого. Как следствие — квадрокоптер будет все время тянуть влево.
Необходим механизм, который бы отслеживал такие отклонения и исправлял их. Характерной особенностью таких ошибок является то, что они прявляют себя со временем. На помощь приходит интегральное слагаемое. Оно хранит сумму всех ошибкок по всем итерациям цикла обработки. Как же это поможет? Если пропорционального слагаемого не достаточно, чтобы исправить маленькую ошибку, но она все равно есть — постепенно, со временем, набирает силы интегральное слагаемое, увеличивая реакцию и квадрокоптер принимает требуемый угол крена.
Тут есть нюанс. Предположим равна 1 градусу, цикл регулирования — 0.1с. Тогда за одну секунду сумма ошибок примет значение 10 градусов. А если цикл обработки — 0.01с, то сумма наберет аж 100 градусов. Чтобы за одно и тоже время интегральное слагаемое набирало одно и тоже значение при разных периодах регулирования, полученную сумму будем умножать на сам период регулирования. Легко посчитать, что в обоих случаях из примера получается сумма в 1 градус. Вот оно — интегральное слагаемое (пока без настраиваемого коэффициента):
.
Эта формула — не что иное, как численный интеграл по времени функции в интервале от нуля до текущего момента. Именно поэтому слагаемое называется интегральным:
,
где T — текущий момент времени.
Пришло время записать окончательную формулу пропорционально-интергрально-дифференциального регулятора:
,
где — один из настраиваемых параметров, которых теперь трое: . Эта формула удобна в применении из программного кода, а вот формула, которая приводится в учебниках:
.
Существует несколько ее вариаций, например, можно ограничить модуль интегрального слагаемого, чтобы он не превысил определенный допустимый порог (мы так и будем делать).
Ну а теперь пришло время для практики подбора коэффициентов. Читателям предлагается JavaScript-страничка с виртуальным квадрокоптером, который он уже видел на картинках: подбор параметров PID-регулятора для квадрокоптера (JSFiddle). При первом запуске сразу видно перерегулирование — колебания вокруг требуемого положения. Когда колебания останавливаются, можно наблюдать эффект, что пропорциональный коэффициент не справляется с ошибкой из-за «несимметричного» квадрокоптера (задается галочкой «Asymmetry»). Для настройки доступны параметры P, I, D. Теперь вы знаете что с ними делать. «Скролом» под квадрокоптером можно управлять требуемым значением крена. «Interval (ms):» — интервал регулирования. Уменьшать его — «читерство», но посмотреть как он влияет на качество стабилизации — очень полезно.Для любителей «чистой» математики можно предложить настроить абстрактный ПИД-регулятор
Введенные параметры автоматически не применяются: нужно жмакать «Apply». Пара небольших советов: если вам кажется, что квадрокоптер слишком медленно реагирует на управление — можно увеличить P, но слишком большое значение P может привести к перерегулированию. С перерегулированием поможет справиться параметр D, но слишком большие значения приведут к частым колебаниям, или опять к перерегулированию. Параметр I, обычно, в 10 — 100 раз меньше, чем параметр P т.к. его сила в накоплении во времени, а не в быстром реагировании.
Ручная настройка ПИД-параметров требует практики. Существуют аналитические методы их вычисления, но они требуют хорошей подготовки и точного знания многих параметров конкретной настраиваемой системы. Как среднее между ручным подбором и аналитическим вычислением есть широкий ряд эмпирических методов, предложенных различными исследователями.
В нашем 2D квадрокоптере меняется только один угол — угол крена. В настроящем 3D квадрокоптере потребуется три независимых ПИД-регулятора для каждого из углов, а управление конкретным мотором будет представлять сумму усилий по всем регуляторам.
В этой статье мы познакомились с базовыми понятиями: квадрокоптер и принцип полета, тангаж, крен, рыскание, газ, газ висения, режим полета stabilize, полетный контроллер, гироскоп, акселерометр, регулятор скорости, ШИМ, калибровка регуляторов, калибровка радио, бортовой приемник, интерфейс настройки полетного контроллера, состояния armed/disarmed, автодизарм.После этого мы заново изобрели формулу ПИД-регулятора немного каснувшись численного дифференцирования и интегрирования, и на своей шкуре испытали, как настраивать параметры P, I, D на виртуальном квадрокоптере.
Теперь, если вы владеете световым мечем-программированием, вы можете приступать к своей программе стабилизации квадрокоптера, или, еще лучше, присоединиться со свежими идеями к существующими open source проектам. Ну а я через неделю-другую, когда появятся силы и время, чтобы соответствовать качеству, продолжу рассказ, как это все программировалось, тестировалось, падало, резало мне пальцы и вовсе улетало в неизвестном направлении. Если вам очень захотелось продолжения — можете напнуть меня здесь или, например, Вконтакте: это немного придает стимула.
В заключении этой части я просто обязан упомянуть человека, который помогал мне в выборе комплектующих и настройке самого сложного (первого!) квадрокоптера на прошивке MegapirateNG и терпеливо отвечал на сотни вопросов по этим самым базовым понятиям: SovGVD, спасибо тебе! 🙂
В награду тем, кто смог промотать всю эту простыню, выкладываю обещанное маленькое видео, как наш квадрокоптер с нашими «изобретенными» ПИД-регуляторами, на нашей программе для Arduino Mega 2560 летает:
Конечно, ему не хватает GPS, как в коммерческих и массовых продуктах, немного не хватает устойчивости, но зато — НАШ, и мы знаем его вдоль и поперек до последнего множителя при интегральном коэффициенте! И это действительно круто, что сегодня нам доступны такие технологии.
habr.com