Ряды номиналов резисторов – Таблица рядов сопротивления резисторов: номинал Е 24 — диспротект.рф

09.05.2021| alexxlab| Нет комментариев

Ряды номиналов резисторов – Таблица рядов сопротивления резисторов: номинал Е 24

Содержание

Номиналы резисторов, ряды резисторов, ряд Е24

Поиск по сайту

Номиналы резисторов представлены так называемыми рядами резисторов (например ряд Е24). Ряды резисторов являются результатом стандартизации номинальных значений резисторов. Для постоянных резисторов существует шесть, так называемых, рядов: Е6, Е12, Е24, Е48, Е96 и Е192, а для переменных резисторов установлен один ряд — Е6. Кроме того существует дополнительный ряд Е3. Цифра после буквы E обозначает число номинальных значений сопротивлений резисторов в каждом десятичном интервале.

Номиналы резисторов соответствуют числам в приведенных ниже таблицах или числам, полученным умножением или делением этих чисел на 10ⁿ (где n – целое положительное или отрицательное число). Например, по ряду Е6 номиналы резисторов в каждой декаде должны соответствовать числам 1; 1,5; 2,2; 3,3; 4,7; 6,8 или числам, полученным умножением или делением этих чисел на 10

n, где n — целое положительное или отрицательное число. Например 10, 100, 15, 150 или 0.1, 0.01, 0.15, 0.015 и т.д. Принцип построения рядов Е48, Е96 и Е192 аналогичен приведенному с той лишь разницей, что увеличивается число промежуточных значений номиналов.

Номиналы резисторов по ряду Е3, Е6, Е12, Е24

Е3	Е6	Е12	Е24	Е3	Е6	Е12	Е24	Е3	Е6	Е12	Е24
1,0	1,0	1,0	1,0	2,2	2,2	2,2	2,2	4,7	4,7	4,7	4,7
			1,1				2,4				5,1
		1,2	1,2			2,7	2,7			5,6	5,6
			1,3				3,0				6,2
	1,5	1,5	1,5		3,3	3,3	3,3		6,8	6,8	6,8
			1,6				3,6				7,5
		1,8	1,8			3,9	3,9			8,2	8,2
			2,0				4,3				9,1

Номиналы резисторов по ряду Е48, Е96, Е192

Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192
100	100	100	147	147	147	215	215	215	316	316	316
		101			149			218			320
	102	102		150	150		221	221		324	324
		104			152			223			328
105	105	105	154	154	154	226	226	226	332	332	332
		106			156			229			336
	107	107		158	158		232	232		340	340
		109			160			234			344
110	110	110	162	162	162	237	237	237	348	348	348
		111			164			240			352
	113	113		165	165		243	243		357	357
		114			167			246			361
115	115	115	169	169	169	249	249	249	365	365	365
		117			172			252			370
	118	118		174	174		255	255		374	374
		120			176			258			379
121	121	121	178	178	178	261	261	261	383	383	383
		123			180			264			388
	124	124		182	182		267	267		392	392
		126			184			271			397
127	127	127	187	187	187	274	274	274	402	402	402
		129			189			277			407
	130	130		191	191		280	280		412	412
		132			193			284			417
133	133	133	196	196	196	287	287	287	422	422	422
		135			198			291			427
		137		200	200		294	294		432	432
		138			203			298			437
140	140	140	205	205	205	301	301	301	442	442	442
		142			208			305			448
	143	143		210	210		309	309		453	453
		145			213			312			459

Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192
464	464	464			556		665	665			796
		470	562	562	562			673		806	806
	475	475			569	681	681	681			816
		481		576	576			690	825	825	825
487	487	487			583		698	698			835
		493	590	590	590			706		845	845
	499	499			597	715	715	715			856
		505		604	604			723	866	866	866
511	511	511			612		732	732			876
		517	619	619	619			741		887	887
	523	523			626	750	750	750			898
		530		634	634			759	909	909	909
536	536	536			642		768	768			920
		542	649	649	649			777		931	931
	549	549			657	787	787	787			942
									953	953	953
											965
										976	976
											988

katod-anod.ru

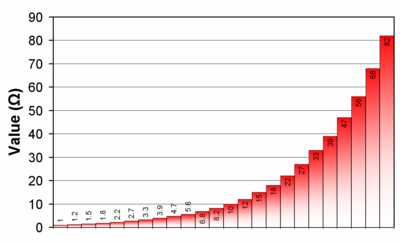Ряды номиналов радиодеталей — это… Что такое Ряды номиналов радиодеталей?

Графическое представление ряда номиналов резисторов Е12

Номиналы промышленно выпускаемых радиодеталей (сопротивление резисторов, ёмкость конденсаторов, индуктивность небольших катушек индуктивности) не являются произвольными. Существуют специальные ряды номиналов, представляющие собой множества значений от 1 до 10. Номинал детали определённого ряда является произвольным значением из соответствующего множества, умноженным на произвольный десятичный множитель (10 в целой степени). Например: резистор из ряда E12 может иметь один из следующих номиналов (сопротивлений):

1,2 Ом
12 Ом
120 Ом
…
1,2 МОм
12 МОм

Номинальные ряды E6, E12, E24

Название ряда указывает общее число элементов в нём, т. е. ряд E24 содержит 24 числа в интервале от 1 до 10, E12 — 12 чисел и т. д.

Каждый ряд соответствует определённому допуску в номиналах деталей. Так, детали из ряда E6 имеют допустимое отклонение от номинала ±20 %, из ряда E12 — ±10 %, из ряда E24 — ±5 %. Собственно, ряды устроены таким образом, что следующее значение отличается от предыдущего чуть меньше, чем на двойной допуск.

Значения номиналов для некоторых рядов приведены в таблице:

**Номинальные ряды E3, E6, E12, E24**
E3	E6	E12	E24
1,0	1,0	1,0	1,0
			1,1
		1,2	1,2
			1,3
	1,5	1,5	1,5
			1,6
		1,8	1,8
			2,0
2,2	2,2	2,2	2,2
			2,4
		2,7	2,7
			3,0
	3,3	3,3	3,3
			3,6
		3,9	3,9
			4,3
4,7	4,7	4,7	4,7
			5,1
		5,6	5,6
			6,2
	6,8	6,8	6,8
			7,5
		8,2	8,2
			9,1

Видно, что ряд E12 получается вычёркиванием из ряда E24 каждого второго номинала, аналогично, E6 получается вычёркиванием из E12 каждого второго номинала.

Простая формула для получения значений номиналов: V(n) = Round(100*exp((n-1)/N*ln(10))), где V(n) значение n-го номинала в классе E-N (N=192,96,48,24,12,6,3).

Принципы построения рядов

Ряд E24 приблизительно представляет собой геометрическую прогрессию со знаменателем 10^1/24. Другими словами, в логарифмическом масштабе элементы этого ряда делят отрезок от 1 до 10 на 24 равные части. По некоторым, видимо историческим, соображениям некоторые элементы отличаются от идеальной прогрессии, хотя и никогда не больше, чем на 2,5 %. Номинальные ряды с меньшим количеством элементов получаются вычёркиванием элементов из ряда E24 через один. Номиналы из этих рядов образуют примерно геометрическую прогрессию со знаменателем 10^1/12 (E12), 10^1/6 (E6), 10^1/3 (E3). Ряд E3 практически не применяется. Номинальные ряды с большим числом элементов образуют уже абсолютно точную геометрическую прогрессию со знаменателем 10^1/n, где n — число элементов ряда. Число n всегда представляет собой степень двойки, умноженную на 3.

Номинальный ряд по сути своей представляет собой таблицу десятичных логарифмов. Действительно, порядковый номер элемента в ряду минус 1 даёт мантиссу логарифма в виде простой дроби со знаменателем (m − 1)/n (m — номер элемента, n — порядок ряда, например, 24 для E24). Зная наизусть ряд E24, можно, таким образом, в уме вычислять произведения чисел, корни небольших степеней из чисел, логарифмы чисел с точностью, примерно ±5 %. Например, вычислим квадратный корень из 1000. Десятичный логарифм этого числа равен 3, поделив его пополам, находим, что десятичный логарифм ответа 1,5 = 1 + 12/24, т. е. ответ есть 10 умноженное на элемент, стоящий в ряду E24 на 13-м месте, т. е. точно в середине ряда, т. е. получили примерно 33.

Есть универсальный способ определения номинала для любого ряда V(n)=(10^n)^(1/m), где m — номер ряда, а n=0;1;2;…;m-1. (Бодиловский В.Г., Смирнов М.А. Справочник молодого радиста. Изд. 3-е. перераб. и доп. М, «Высш. школа», 1976)

Номинальные ряды с большим числом элементов

Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %. Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 10^1/48 ≈ 1,04914, 10^1/96 ≈ 1,024275, 10^1/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.

**Номинальные ряды E48, E96, E192**
E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192
1,00	1,00	1,00	1,47	1,47	1,47	2,15	2,15	2,15	3,16	3,16	3,16	4,64	4,64	4,64	6,81	6,81	6,81
		1,01			1,49			2,18			3,20			4,70			6,90
	1,02	1,02		1,50	1,50		2,21	2,21		3,24	3,24		4,75	4,75		6,98	6,98
		1,04			1,52			2,23			3,28			4,81			7,06
1,05	1,05	1,05	1,54	1,54	1,54	2,26	2,26	2,26	3,32	3,32	3,32	4,87	4,87	4,87	7,15	7,15	7,15
		1,06			1,56			2,29			3,36			4,93			7,23
	1,07	1,07		1,58	1,58		2,32	2,32		3,40	3,40		4,99	4,99		7,32	7,32
		1,09			1,60			2,34			3,44			5,05			7,41
1,10	1,10	1,10	1,62	1,62	1,62	2,37	2,37	2,37	3,48	3,48	3,48	5,11	5,11	5,11	7,50	7,50	7,50
		1,11			1,64			2,40			3,52			5,17			7,59
	1,13	1,13		1,65	1,65		2,43	2,43		3,57	3,57		5,23	5,23		7,68	7,68
		1,14			1,67			2,46			3,61			5,30			7,77
1,15	1,15	1,15	1,69	1,69	1,69	2,49	2,49	2,49	3,65	3,65	3,65	5,36	5,36	5,36	7,87	7,87	7,87
		1,17			1,72			2,52			3,70			5,42			7,96
	1,18	1,18		1,74	1,74		2,55	2,55		3,74	3,74		5,49	5,49		8,06	8,06
		1,20			1,76			2,58			3,79			5,56			8,16
1,21	1,21	1,21	1,78	1,78	1,78	2,61	2,61	2,61	3,83	3,83	3,83	5,62	5,62	5,62	8,25	8,25	8,25
		1,23			1,80			2,64			3,88			5,69			8,35
	1,24	1,24		1,82	1,82		2,67	2,67		3,92	3,92		5,76	5,76		8,45	8,45
		1,26			1,84			2,71			3,97			5,83			8,56
1,27	1,27	1,27	1,87	1,87	1,87	2,74	2,74	2,74	4,02	4,02	4,02	5,90	5,90	5,90	8,66	8,66	8,66
		1,29			1,89			2,77			4,07			5,97			8,76
	1,30	1,30		1,91	1,91		2,80	2,80		4,12	4,12		6,04	6,04		8,87	8,87
		1,32			1,93			2,84			4,17			6,12			8,98
1,33	1,33	1,33	1,96	1,96	1,96	2,87	2,87	2,87	4,22	4,22	4,22	6,19	6,19	6,19	9,09	9,09	9,09
		1,35			1,98			2,91			4,27			6,26			9,19
	1,37	1,37		2,00	2,00		2,94	2,94		4,32	4,32		6,34	6,34		9,31	9,31
		1,38			2,03			2,98			4,37			6,42			9,42
1,40	1,40	1,40	2,05	2,05	2,05	3,01	3,01	3,01	4,42	4,42	4,42	6,49	6,49	6,49	9,53	9,53	9,53
		1,42			2,08			3,05			4,48			6,57			9,65
	1,43	1,43		2,10	2,10		3,09	3,09		4,53	4,53		6,65	6,65		9,76	9,76
		1,45			2,13			3,12			4,59			6,73			9,88

Стандарты ISO
Перечни: Перечень стандартов ИСО • Перечень романизаций ISO • Перечень стандартов IEC Категории: Категория:Стандарты ISO • Категория:Протоколы OSI
1 по 9999	1 • 2 • 3 • 4 • 5 • 6 • 7 • 9 • 16 • 31 (-0, -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, -12, -13) • 128 • 216 • 217 • 226 • 228 • 233 • 259 • 269 • 296 • 302 • 306 • 428 • 639 (-1, -2, -3, -5, -6) • 646 • 690 • 732 • 764 • 843 • 898 • 1000 • 1004 • 1007 • 1073-1 • 1413 • 1538 • 1745 • 2014 • 2015 • 2022 • 2108 • 2145 • 2146 • 2281 • 2709 • 2711 • 2788 • 3029 • 3103 • 3166 (-1, -2, -3) • 3297 • 3307 • 3602 • 3864 • 3901 • 3977 • 4031 • 4157 • 4217 • 5218 • 5775 • 5776 • 5964 • 6166 • 6344 • 6346 • 6425 • 6429 • 6438 • 6523 • 6709 • 7001 • 7002 • 7098 • 7185 • 7388 • 7498 • 7736 • 7810 • 7811 • 7812 • 7813 • 7816 • 8000 • 8217 • 8571 • 8583 • 8601 • 8632 • 8652 • 8691 • 8807 • 8820-5 • 8859 (-1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, -12, -13, -14, -15, -16) • 8879 • 9000 • 9075 • 9126 • 9241 • 9362 • 9407 • 9506 • 9529 • 9564 • 9594 • 9660 • 9897 • 9945 • 9984 • 9985 • 9995
10000 по 19999	10006 • 10118-3 • 10160 • 10161 • 10165 • 10179 • 10206 • 10303 • 10303-11 • 10303-21 • 10303-22 • 10303-238 • 10303-28 • 10383 • 10487 • 10585 • 10589 • 10646 • 10664 • 10746 • 10861 • 10957 • 10962 • 10967 • 11073 • 11170 • 11179 • 11404 • 11544 • 11783 • 11784 • 11785 • 11801 • 11898 • 11940 • 11941 • 11941 (TR) • 11992 • 12006 • 12164 • 12182:1998 • 12207:1995 • 12207:2008 • 12234-2 • 13211 (-1, -2) • 13216 • 13250 • 13399 • 13406-2 • 13407 • 13450 • 13485 • 13490 • 13567 • 13568 • 13584 • 13616 • 14000 • 14031 • 14396 • 14443 • 14496-10 • 14496-14 • 14644 (-1, -2, -3, -4, -5, -6, -7, -8, -9) • 14649 • 14651 • 14698 • 14698-2 • 14750 • 14882 • 14971 • 15022 • 15189 • 15288 • 15291 • 15292 • 15408 • 15444 • 15445 • 15438 • 15504 • 15511 • 15686 • 15693 • 15706 • 15706-2 • 15707 • 15897 • 15919 • 15924 • 15926 • 15926 WIP • 15930 • 16023 • 16262 • 16750 • 17024 • 17025 • 17369 • 17799 • 18000 • 18004 • 18014 • 18245 • 18629 • 18916 • 19005 • 19011 • 19092-1 • 19092-2 • 19114 • 19115 • 19439 • 19501:2005 • 19752 • 19757 • 19770 • 19775-1 • 19794-5
20000+	20000 • 20022 • 21000 • 21047 • 21827:2002 • 22000 • 23008-2 • 23270 • 23360 • 24613 • 24707 • 25178 • 26000 • 26300 • 26324 • 27000 series • 27000 • 27001 • 27002 • 27003 • 27004 • 27005 • 27006 • 27007 • 27729 • 27799 • 29199-2 • 29500 • 31000 • 32000 • 38500 • 42010 • 50001 • 80000
См. также: Все статьи, начинающиеся с «ISO»

dic.academic.ru

Ряды номинальных сопротивлений резисторов (Е48-Е192)

Ряды номинальных сопротивлений резисторов

Номинальные сопротивления резисторов, выпускаемых отечественной промышленностью в соответствии с рекомендациями МЭК, стандартизованы. Для постоянных резисторов установлено шесть рядов: Е6, Е12, Е24, Е48, Е96, Е192, а для переменных резисторов установлен ряд Е6. Кроме этого допускается использовать ряд Е3. Цифра после буквы Е указывает число номинальных значений в каждом десятичном интервале. Номиналы сопротивлений соответствуют числам в приведенных ниже таблицах или числам, полученным умножением или делением этих чисел на 10ⁿ (n — целое положительное или отрицательное число).

Номинальные сопротивления по ряду Е48, Е96, Е192

Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192
100	100	100	147	147	147	215	215	215	316	316	316
		101			149			218			320
	102	102		150	150		221	221		324	324
		104			152			223			328
105	105	105	154	154	154	226	226	226	332	332	332
		106			156			229			336
	107	107		158	158		232	232		340	340
		109			160			234			344
110	110	110	162	162	162	237	237	237	348	348	348
		111			164			240			352
	113	113		165	165		243	243		357	357
		114			167			246			361
115	115	115	169	169	169	249	249	249	365	365	365
		117			172			252			370
	118	118		174	174		255	255		374	374
		120			176			258			379
121	121	121	178	178	178	261	261	261	383	383	383
		123			180			264			388
	124	124		182	182		267	267		392	392
		126			184			271			397
127	127	127	187	187	187	274	274	274	402	402	402
		129			189			277			407
	130	130		191	191		280	280		412	412
		132			193			284			417
133	133	133	196	196	196	287	287	287	422	422	422
		135			198			291			427
		137		200	200		294	294		432	432
		138			203			298			437
140	140	140	205	205	205	301	301	301	442	442	442
		142			208			305			448
	143	143		210	210		309	309		453	453
		145			213			312			459

Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192	Е48	Е96	Е192
464	464	464			556		665	665			796
		470	562	562	562			673		806	806
	475	475			569	681	681	681			816
		481		576	576			690	825	825	825
487	487	487			583		698	698			835
		493	590	590	590			706		845	845
	499	499			597	715	715	715			856
		505		604	604			723	866	866	866
511	511	511			612		732	732			876
		517	619	619	619			741		887	887
	523	523			626	750	750	750			898
		530		634	634			759	909	909	909
536	536	536			642		768	768			920
		542	649	649	649			777		931	931
	549	549			657	787	787	787			942
									953	953	953
											965
										976	976
											988

studfiles.net

Ряды номиналов радиодеталей

Номиналы промышленно выпускаемых радиодеталей (сопротивление резисторов, ёмкость конденсаторов, индуктивность небольших катушек индуктивности) имеют отнюдь не произвольные значения, а берутся из специальных номинальных рядов. Точнее, номиналы деталей могут быть произвольным числом из соответствующего ряда, умноженным на произвольный десятичный множитель (десять в произвольной (целой?) степени), например резистор из ряда E12 может иметь сопротивление 1,2 Ом, 12 Ом, 120 Ом, …, 1,2 МОм, 12 МОм, 1,5 Ом, 15 Ом и т. д.

Компания «Новый свет» поставляет радиодетали любых номиналов. Посмотрите каталог электронных компонентов здесь. Мы продаем светодиоды DIP, светодиоды SMD; тонкопленочные, металлокерамические и SMD резисторы; светодиоды сверхяркие (Пиранья), цоколи для изготовления ламп, радиаторы для светодиодов, мощные светодиоды от 1Вт, алюминиевые платы для светодиодов, светодиодную оптику.

Указание на схемах номиналов элементов, не принадлежащих никакому ряду без особого технического обоснования, считается неграмотностью. Поэтому хорошие радиоинженеры помнят ряд E24 наизусть. Значения номиналов для некоторых рядов приведены в таблице:

Номинальные ряды E6, E12, E24
E6	E12	E24	E6	E12	E24	E6	E12	E24
1,0	1,0	1,0	2,2	2,2	2,2	4,7	4,7	4,7
		1,1			2,4			5,1
	1,2	1,2		2,7	2,7		5,6	5,6
		1,3			3,0			6,2
1,5	1,5	1,5	3,3	3,3	3,3	6,8	6,8	6,8
		1,6			3,6			7,5
	1,8	1,8		3,9	3,9		8,2	8,2
		2,0			4,3			9,1

Ряд E24 приблизительно представляет собой геометрическую прогрессию со знаменателем 101/24. Другими словами, в логарифмическом масштабе элементы этого ряда делят отрезок от 1 до 10 на 24 равные части. По некоторым, видимо историческим, соображениям некоторые элементы отличаются от идеальной прогрессии, хотя и никогда не больше, чем на 2,5 %. Номинальные ряды с меньшим количеством элементов получаются вычёркиванием элементов из ряда E24 через один. Номиналы из этих рядов образуют примерно геометрическую прогрессию со знаменателем 101/12 (E12), 101/6 (E6), 101/3 (E3). Ряд E3 практически не применяется. Номинальные ряды с большим числом элементов образуют уже абсолютно точную геометрическую прогрессию со знаменателем 101/n, где n — число элементов ряда. Число n всегда представляет собой степень двойки, умноженную на 3.

Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %. Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 101/48 ≈ 1,04914, 101/96 ≈ 1,024275, 101/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.

Номинальные ряды E48, E96, E192
E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192	E48	E96	E192
1,00	1,00	1,00	1,47	1,47	1,47	2,15	2,15	2,15	3,16	3,16	3,16	4,64	4,64	4,64	6,81	6,81	6,81
		1,01			1,49			2,18			3,20			4,70			6,90
	1,02	1,02		1,50	1,50		2,21	2,21		3,24	3,24		4,75	4,75		6,98	6,98
		1,04			1,52			2,23			3,28			4,81			7,06
1,05	1,05	1,05	1,54	1,54	1,54	2,26	2,26	2,26	3,32	3,32	3,32	4,87	4,87	4,87	7,15	7,15	7,15
		1,06			1,56			2,29			3,36			4,93			7,23
	1,07	1,07		1,58	1,58		2,32	2,32		3,40	3,40		4,99	4,99		7,32	7,32
		1,09			1,60			2,34			3,44			5,05			7,41
1,10	1,10	1,10	1,62	1,62	1,62	2,37	2,37	2,37	3,48	3,48	3,48	5,11	5,11	5,11	7,50	7,50	7,50
		1,11			1,64			2,40			3,52			5,17			7,59
	1,13	1,13		1,65	1,65		2,43	2,43		3,57	3,57		5,23	5,23		7,68	7,68
		1,14			1,67			2,46			3,61			5,30			7,77
1,15	1,15	1,15	1,69	1,69	1,69	2,49	2,49	2,49	3,65	3,65	3,65	5,36	5,36	5,36	7,87	7,87	7,87
		1,17			1,72			2,52			3,70			5,42			7,96
	1,18	1,18		1,74	1,74		2,55	2,55		3,74	3,74		5,49	5,49		8,06	8,06
		1,20			1,76			2,58			3,79			5,56			8,16
1,21	1,21	1,21	1,78	1,78	1,78	2,61	2,61	2,61	3,83	3,83	3,83	5,62	5,62	5,62	8,25	8,25	8,25
		1,23			1,80			2,64			3,88			5,69			8,35
	1,24	1,24		1,82	1,82		2,67	2,67		3,92	3,92		5,76	5,76		8,45	8,45
		1,26			1,84			2,71			3,97			5,83			8,56
1,27	1,27	1,27	1,87	1,87	1,87	2,74	2,74	2,74	4,02	4,02	4,02	5,90	5,90	5,90	8,66	8,66	8,66
		1,29			1,89			2,77			4,07			5,97			8,76
	1,30	1,30		1,91	1,91		2,80	2,80		4,12	4,12		6,04	6,04		8,87	8,87
		1,32			1,93			2,84			4,17			6,12			8,98
1,33	1,33	1,33	1,96	1,96	1,96	2,87	2,87	2,87	4,22	4,22	4,22	6,19	6,19	6,19	9,09	9,09	9,09
		1,35			1,98			2,91			4,27			6,26			9,19
	1,37	1,37		2,00	2,00		2,94	2,94		4,32	4,32		6,34	6,34		9,31	9,31
		1,38			2,03			2,98			4,37			6,42			9,42
1,40	1,40	1,40	2,05	2,05	2,05	3,01	3,01	3,01	4,42	4,42	4,42	6,49	6,49	6,49	9,53	9,53	9,53
		1,42			2,08			3,05			4,48			6,57			9,65
	1,43	1,43		2,10	2,10		3,09	3,09		4,53	4,53		6,65	6,65		9,76	9,76
		1,45			2,13			3,12			4,59			6,73			9,88

led61.ru

Ряды номиналов радиодеталей — Приднестровский портал радиолюбителей

Номиналы промышленно выпускаемых радиодеталей (сопротивление резисторов, ёмкость конденсаторов, индуктивность небольших катушек индуктивности) имеют отнюдь не произвольные значения, а берутся из специальных номинальных рядов. Точнее, номиналы деталей могут быть произвольным числом из соответствующего ряда, умноженным на произвольный десятичный множитель (десять в произвольной степени), например резистор из ряда E12 может иметь сопротивление 1,2 Ом, 12 Ом, 120 Ом, …, 1,2 МОм, 12 МОм, 1,5 Ом, 15 Ом и т. д.
Номинальные ряды E6, E12, E24

Принципы построения рядов

radio-hobby.org

Декодер цветовой маркировки резисторов. 3,4,5,6 полос

Примеры цветовой маркировки 1% резисторов
(5 полос) 1-9.76 Ом10-97.6 Ом100-976 Ом1-9.76 кОм10-97.6 кОм100-976 кОм1-9.76 МОм

Вариант1: для расчета цвет — номинал выберите цвет полос и

Примеры цветовой маркировки 5% резисторов (4 полосы) 0.1-910 Ом1кОм-10 MОм

0.1 Ом, цветовая маркировка: коричневый, черный, серебристый, золотистый

0.11 Ом

0.12 Ом

0.13 Ом

0.15 Ом

0.16 Ом

0.18 Ом

0.2 Ом

0.22 Ом

0.24 Ом

0.27 Ом

0.3 Ом

0.33 Ом

0.36 Ом

0.39 Ом

0.43 Ом

0.47 Ом

0.51 Ом

0.56 Ом

0.62 Ом

0.68 Ом

0.75 Ом

0.82 Ом

0.91 Ом

1 Ом цветовая маркировка резистора: коричневый, черный, золотистый, золотистый

1.1 Ом

1.2 Ом

1.3 Ом

1.5 Ом

1.6 Ом

1.8 Ом

2 Ом

2.2 Ом

2.4 Ом

2.7 Ом

3 Ом

3.3 Ом

3.6 Ом

3.9 Ом

4.3 Ом

4.7 Ом

5.1 Ом

5.6 Ом

6.2 Ом

6.8 Ом

7.5 Ом

8.2 Ом

9.1 Ом

10 Ом , цветовая маркировка резистора: коричневый, черный, черный, золотистый

11 Ом

12 Ом

13 Ом

15 Ом , цветовая маркировка резистора: коричневый, зеленый, черный, золотистый

16 Ом

18 Ом

20 Ом

22 Ом

24 Ом

27 Ом

30 Ом

33 Ом

36 Ом

39 Ом

43 Ом

47 Ом

51 Ом

56 Ом

62 Ом

68 Ом

75 Ом

82 Ом

91 Ом

100 Ом , цветовая маркировка резистора: коричневый, черный, коричневый, золотистый

110 Ом

120 Ом

130 Ом

150 Ом

160 Ом

180 Ом

200 Ом

220 Ом

240 Ом

270 Ом

300 Ом

330 Ом

360 Ом

390 Ом

430 Ом

470 Ом

510 Ом

560 Ом

620 Ом

680 Ом

750 Ом

820 Ом

910 Ом

1к 5%, цветовая маркировка: коричневый, черный, красный, золотистый

1.1к

1.2к

1.3к

1.5к 5%, цветовая маркировка: коричневый, зеленый, красный, золотистый

1.6к

1.8к

2к

2.2к

2.4к

2.7к

3к

3.3к

3.6к

3.9к

4.3к

4.7к

5.1к

5.6к

6.2к

6.8к

7.5к

8.2к

9.1к

10к 5%, цветовая маркировка: коричневый, черный, оранжевый, золотистый

11к

12к

13к

15к 5%, цветовая маркировка: коричневый, зеленый, красный, золотистый

16к

18к

20к

22к

24к

27к

30к

33к

36к

39к

43к

47к

51к

56к

62к

68к

75к

82к

91к

100к 5%, цветовая маркировка: коричневый, черный, Желтый, золотистый

110к

120к

130к

150к

160к

180к

200к

220к

240к

270к

300к

330к

360к

390к

430к

470к

510к

560к

620к

680к

750к

820к

910к

1 M 5%, цветовая маркировка: коричневый, черный, зеленый, золотистый

1.1 M

1.2 M

1.3 M

1.5 M 5%, цветовой код: коричневый, зеленый, зеленый, золотистый

1.6 M

1.8 M

2 M

2.2 M

2.4 M

2.7 M

3 M

3.3 M

3.6 M

3.9 M

4.3 M

4.7 M

5.1 M

5.6 M

6.2 M

6.8 M

7.5 M

8.2 M

9.1 M

E12	E24	E48	E96	E192
10%	5%	2%	1%	0.5%

Возможности декодера цветовой маркировки резисторов.

Расчет номинала резистора по цветовому коду:
укажите количество цветных полос и выберите цвет каждой из них (меню выбора цвета находится под каждой полоской). Результат будет выведен в поле «РЕЗУЛЬТАТ»

Расчет цветового кода для заданного значения сопротивления:
Введите значение в поле «РЕЗУЛЬТАТ» и укажите требуемую точность резистора. Полоски маркировки на изображении резистора будут окрашены соответствующим образом. Количество полос декодер подбирает по следующему принципу: приоритет у 4-полосной маркировки резисторов общего назначения, и только если резисторов общего назначения с таким номиналом не существует, выводится 5-ти полосная маркировка 1% или 0.5% резисторов.

Назначение кнопки «РЕВЕРС»:
При нажатии на эту кнопку цветовой код резистора будет перестроен зеркальным образом от исходного. Таким образом можно узнать, возможно ли чтение цветового кода в обратном направлении (справа — налево). Эта функция калькулятора нужна в том случае, когда сложно понять, какая полоска в цветовой маркировке резистора является первой. Обычно первая полоска или толще остальных, или расположена ближе к краю резистора. Но в случаях 5-ти и 6-ти полосной цветовой маркировки прецизионных резисторов может не хватить места, чтобы сместить полоски маркировки к одному краю. А толщина полосок может отличаться весьма незначительно… С 4-полосной маркировкой 5% и 10% резисторов общего назначения все проще: последняя полоска, обозначающая точность — золотистого или серебристого цвета, а эти цвета никак не могут быть у первой полоски.

Назначение кнопки «М+»:
Эта кнопка позволит сохранить в памяти текущую цветовую маркировку. Сохраняется до 9 цветовых маркировок резисторов. Кроме того, автоматически сохраняются в память калькулятора все значения, выбранные из колонок примеров цветовой маркировки, из таблицы значений в стандартных рядах, любые значения (правильные и неправильные), введенные в поле «Результат», и только правильные значения, введенные с помощью меню выбора цвета полосок либо кнопок «+» и «-«. Функция удобна, когда требуется определить цветовую маркировку нескольких резисторов — всегда можно быстро вернуться к маркировке любого из уже проверенных. Красным цветом в списке обозначаются значения с ошибочной и нестандартной цветовой маркировкой (значение не принадлежит к стандартным рядам, кодированный цветом допуск на резисторе не соответствует допуску стандартного ряда, к которому относится значение и т.д.).

Кнопка «MC»: — очистка всей памяти. Для удаления из списка только одной записи покройте оную двойным кликом.

Назначение кнопки «Исправить»:
При нажатии на эту кнопку (если в цветовом коде резистора допущена ошибка) будет предложен один из возможных правильных вариантов.

Назначение кнопок «+» и «-» :
При нажатии на них значение в соответствующей полоске изменится на один шаг в большую или меньшую сторону.

Назначение информационное поля (под полем «РЕЗУЛЬТАТ»):
В нем выводятся сообщения, к каким стандартным рядам принадлежит введенное значение (с какими допусками резисторы этого номинала выпускаются промышленностью), а так же сообщения об ошибках. Если значение не является стандартным, то либо вы допустили ошибку, либо производитель резистора не придерживается общепринятого стандарта (что случается).

Примеры цветовой кодировки резисторов:
Слева приведены примеры цветовой маркировки 1%, а справа — 5% резисторов. Кликните по значению в списке, и полоски на изображении резистора будут перекрашены в соответствующие цвета.

Таблица, расположенная выше, содержит стандартные значения сопротивлений. Таблица автоматически прокручивается до значений, которые находятся ближе всего к величине, заданной цветовым кодом на изображении резистора. Практически все номиналы постоянных резисторов, которые выпускаются промышленностью, берутся из стандартных рядов и получены умножением значения из стандартного ряда на 10 в определенной степени (номинал в данном случае в Омах, т.е. 28.7кОм = стандартное значение 287, умноженное на 10 в степени 2 /Ом/). Каждому ряду соответствует своя точность резисторов.

www.searchingtabs.com

Ряды номинальных сопротивлений (Е3-Е24)

Ряды номинальных сопротивлений резисторов

Номинальные сопротивления по ряду Е3, Е6, Е12, Е24

Е3	Е6	Е12	Е24	Е3	Е6	Е12	Е24
1,0	1,0	1,0	1,0		3,3	3,3	3,3
			1,1				3,6
		1,2	1,2			3,9	3,9
			1,3				4,3
	1,5	1,5	1,5	4,7	4,7	4,7	4,7
			1,6				5,1
		1,8	1,8			5,6	5,6
			2,0				6,2
2,2	2,2	2,2	2,2		6,8	6,8	6,8
			2,4				7,5
		2,7	2,7			8,2	8,2
			3,0				9,1

studfiles.net

"ДИС-Протект"