Сглаживание сигнала – Сглаживание цифровых сигналов / Habr

Сглаживание цифровых сигналов / Habr

Введение

Данную статью меня заставил написать пост habrahabr.ru/post/183986, где не совсем правильно используется некоторый алгоритм сглаживания изображения.

Сразу перейдём к сути дела.

Математические модели цифровых сигналов — вектора и матрицы, элементами которых являются числа. Числа могут быть двоичными (бинарный сигнал), десятичными («обычный» сигнал) и так далее. Любой звук, любое изображение и видео могут быть преобразованы в цифровой сигнал¹: звук — в вектор, изображение — в матрицу, а видео — в последовательный набор матриц. Поэтому цифровой сигнал — это, можно сказать, универсальный объект для представления информации.

Задача сглаживания — это, по сути, задача фильтрации сигнала от скачкообразных (ступенчатых) изменений. Считается, что полезный сигнал их не содержит. Ступенчатый сигнал за счёт множества резких, но небольших по амплитуде, перепадов уровня содержит высокочастотные составляющие, которых нет в сглаженном сигнале. Поэтому для некоторого алгоритма сглаживания в первую очередь необходимо определить как сильно ослабляются разные частотные составляющие. Другими словами, необходимо построить амплитудно-частотную характеристику соответствующего фильтра, иначе велика вероятность «нарваться» на артефакты.

Задача сглаживания может использоваться при прореживании сигналов, то есть когда, например, необходимо отобразить большую картинку на небольшой экран. Или когда частота дискретизации звука снижается, например, с 48000 Гц до 44100 Гц. Понижение частоты выборок — коварная операция, требующая предварительной обработки сигнала (низкочастотной фильтрации), но это — тема отдельного разговора…

Приведём пример «плохого» сглаживания

Казалось бы, обычное усреднение и сигнал на выходе должен быть «гладким». Но как определить, насколько он стал «глаже»? Не переборщили ли мы? А может быть некоторые коэффициенты выбрать не по 1/3? А может быть усреднить по пяти точкам? Как определить насколько ослабляются частотные составляющие в сигнале? Как найти

свой (то есть для конкретной задачи) оптимум?
На эти и некоторые другие вопросы я постараюсь ответить так, чтобы «обычный» программист смог обосновать свой алгоритм, — надеюсь, не только алгоритм на тему «Сглаживание», так как идеи будут излагаться весьма общие, заставляющие думать самому…

Сигналы

В этом параграфе под сигналом понимается вектор, то есть массив из определённого количества чисел. Например, вектор из четырёх элементов s = (2,5; 5; 0; -5).

Для простоты будут рассматриваться только десятичные вещественные числа.

Одним из наиболее распространённых и понятных сигналов является оцифрованный звук. Размер сигнала зависит от длительности звука и от частоты, с которой делают выборки (от частоты дискретизации). Элементы-числа сигнала зависят от текущей амплитуды звука, измеряемой устройством выборки и хранения.

Как уже было сказано, один из самых простых способов сглаживания, это

(1)
где s — исходный сигнал, v — сглаженный сигнал.

Способ (1) основан на сглаживающем свойстве суммирования, ведь каждому ясно, что средняя величина, вычисляемая как сумма многих случайных чисел, с ростом количества суммируемых чисел становится всё менее и менее похожей на случайную величину ², которая, попросту говоря, и есть шум ³.

Но на чём основан выбор коэффициентов в уравнении (1)? На том, что так вычисляется среднее? Вроде бы да, но… А если взять не три слагаемых, а шестнадцать? А тридцать два?.. Почему всё более отстоящие от центрального элемента s[i] отсчёты должны браться с одинаковым весом? Ведь может оказаться так, что связь между отсчётами будет постепенно ослабевать с ростом расстояния ⁴ между ними?

Если рассмотреть пример произношения слова «арбуз» десять раз подряд и попытаться отследить связь между отсчётами записанного сигнала, то можно обнаружить ослабление зависимости между всё более отстоящими друг от друга отсчётами. Естественно, что если рассмотреть «большие расстояния», то звуки будут повторяться за счёт повтора одного и того же слова и зависимость будет нарастать и снова спадать, и так далее. Но, как правило, «большие расстояния» при сглаживании не рассматривают, так как шумы проявляются в окрестности отдельных звуков, а не слов, фраз и предложений. Шум, действующий на уровне слов или даже фраз — это явно искусственный (звуковые эффекты) или экзотический естественный (эхо). Это — уже «неслучайный» шум, требующий отдельного исследования. Здесь рассматривается «чистый» шум, который, говоря простым языком, раздражающе шумит и нисколько не похож на какой-либо полезный сигнал.

На основании простых рассуждений становится очевидным, что количество слагаемых в (1) (порядок фильтра) должно зависеть от того, насколько сильно зависят друг от друга соседние отсчёты. Например, нет смысла брать фильтр тридцатого порядка, если наблюдается зависимость только лишь десяти отсчётов, следующих друг за другом. На самом деле даже не то, что «нет смысла», а — нельзя, так как если отсчёты практически не связаны, то начнётся чрезмерное сглаживание полезного сигнала («съедение» слогов). Но и фильтр третьего порядка здесь не будет оптимальным по степени использования информации о полезном сигнале, так как, как уже было сказано, наблюдается зависимость порядка десяти соседних отсчётов. Поэтому можно «попытать счастья» с помощью фильтра девятого порядка, естественно, увеличив нагрузку на процессор-вычислитель. Здесь уже требуется определить, скорее всего экспериментально, а стоит ли данная игра свеч?..

Как оценить насколько сильно связаны соседние отсчёты? Вычислить автокорреляционную функцию (АКФ). Желающим можно предложить провести эксперимент по записи разных слов, фраз, повторов фраз и последующему построению АКФ (благо, например, программа Matlab позволяет это сделать, особо не задумываясь над кодом и формулами).

Так как всё-таки выбрать коэффициенты фильтра в (1)?

В данном случае удобно рассмотреть реакцию фильтра на единичное воздействие, то есть на сигнал вида

Например, фильтр (1) даст следующий отклик (импульсную характеристику)

откуда мы можем сделать вывод, что после сглаживания длительность сигнала стала равна трём элементам. А если взять фильтр из пяти элементов?.. Правильно, длительность выходного сигнала будет равна пяти элементам. Насколько это полезно, определяется конкретной ситуацией (задачей).

Кстати, а долгожданный артефакт уже налицо! Импульсная характеристика (1) — это, по сути, прямоугольный импульс, нисколько не являющийся гладким!.. Странно, да? А если взять пятиточечный фильтр? Тогда на выходе получим более длинный прямоугольный импульс, но с меньшей амплитудой. Не очень хорошо выходит… Простейший тест говорит о непригодности простого усреднения для сглаживания.

Посмотрим на фильтр (1) с частотной стороны (с временной мы уже посмотрели).

Если сигнал звуковой, то он достаточно хорошо описывается набором гармонических сигналов

5 («синусоид») и степень ослабления конкретной синусоиды зависит от её частоты. Опять же, при грамотном выборе сглаживающего фильтра никакая из полезных синусоид не должна пропадать полностью, то есть амплитудно-частотная характеристика фильтра в рабочем диапазоне частот должна быть достаточно равномерной.

Пропустим через рассматриваемый фильтр один однотональный сигнал определённой частоты, естественно, не выходя за пределы теоремы отсчётов. Пусть шаг дискретизации по времени T_d равен единице, то есть отсчёты идут с шагом одна секунда. Возьмём сигнал с частотой f = 1/(3T_d) = 1/3 Гц, то есть

Ограничимся двумя периодами

Отклик фильтра (1) будет равен

Как ни странно, получили почти ноль… Получается, можно потерять некоторые составляющие полезного сигнала.

Проверим отклик на несколько более высокочастотный сигнал

Как видим, форму сигнала не потеряли. В чём же дело?..

Дело в том, что амплитудно-частотная характеристика фильтра (1) не является монотонной в рабочей полосе частот (в полосе от нуля до половины частоты дискретизации) и имеет один нуль на частоте, в три раза меньшей частоты дискретизации. Как это показать?

Попросту говоря, чтобы определить частотную характеристику фильтра, необходимо найти отношение спектра на выходе фильтра к спектру на входе.

Обозначим спектр сигнала s[i] на входе как S( f ), тогда спектр задержанного на один такт T_d сигнала s[i-1] выразится через спектр исходного сигнала как
(2)
где j — мнимая единица.

Спектр опережённого сигнала s[i+1] выразится как
(3)

Что означает мнимая единица? И как можно обосновать (2) и (3)?
Если записать известные [1, 2] ряды для синуса, косинуса и экспоненты
(4)
то подобрав число

j, такое, что j² = –1, можно последний ряд выразить через два первых
(5)
что означает то, что любое комплексное число можно записать через экспоненту с мнимым показателем. Модуль числа (5) равен единице (корень квадратный из суммы квадратов мнимой и реальной частей), поэтому для записи любого комплексного числа в форме (5) его необходимо разделить и умножить на свой модуль
(6)

Из (5) и (6) следует, что если в показателе экспоненты можно выделить мнимую единицу, умноженную на некоторое действительное число, то это число является аргументом комплексного числа.

В данном случае рассматриваются сигналы, поэтому модулю комплексного числа соответствует амплитуда гармонического сигнала, а аргументу — фаза. Если, например, взять сигнал вида
(7)
то можно выделить амплитуду A и фазу Ф. Множитель — это также фаза, и в некоторых случаях её выносят за скобки. Например, при прохождении сигнала (7) через некоторый фильтр важно знать разность фаз сигналов на входе и выходе, которую вносит фильтр на заданной частоте

f.

Если сигнал (7) задержать на величину t₀, то получится тот же самый сигнал, но сдвинутый по фазе на постоянную величину
(8)
то есть при задержке произвольного сигнала все его частотные составляющие сдвигаются по фазе на величину, зависящую от текущей частоты и величины задержки. Этим можно объяснить формулы (2) и (3). Поэтому при анализе какого-либо алгоритма важна и фазо-частотная характеристика, которая показывает на какое время задерживает фильтр (алгоритм) каждую частотную составляющую входного сигнала. Низкие частоты и высокие в общем случае будут иметь разную задержку в фильтре.

Из (1), (2) и (3) следует, что частотная характеристика фильтра (передаточная функция) будет иметь вид
(9)

Так как спектр выходного сигнала линейно выражается через спектр входного, то при выводе (9) спектр входного сигнала успешно сокращается. Далее замечаем, что частотная характеристика фильтра (1) — действительная, то есть данный фильтр не вносит фазовых искажений

6. Этого мы достигли (скорее всего, неосознанно) за счёт симметричности формулы (1): каждый отсчёт на выходе фильтра равен сумме текущего и двух соседних отсчётов.

Физически такой алгоритм реализуем только при наличии запоминающих устройств, так как в нём используются опережающие отсчёты (для вычисления отсчёта s[i] требуется отсчёт s[i+1]). В настоящее время это не является большой проблемой и, как правило, используют симметричные алгоритмы. Если фазовые искажения окажутся полезными, то — пожалуйста, главное осознанно применять какой-либо алгоритм и смотреть на него с разных сторон: с частотной и временной.

Построить график зависимости (9) от частоты не составляет труда. Для упрощения вводят нормированную частоту f₀  = f T_d , полезный диапазон изменения которой [0…0,5]. Составляющие сигнала с частотами выше половины частоты дискретизации по теореме отсчётов должны отсутствовать (перед оцифровкой сигнал пропускают через соответствующие фильтры нижних частот). Частота дискретизации показывает количество выдаваемых цифровым устройством отсчётов в секунду. Если, например, один такт T_d равен одной миллисекунде, то за одну секунду должна быть выдана тысяча отсчётов.

Анализируя (9) можно заметить, что на некотором промежутке коэффициент передачи меньше нуля, а амплитуда — это по определению положительная величина… Выход из ситуации — построить модуль передаточной функции, убрав знак минус в фазовую характеристику, которая, всё-таки, не является константой (нулём). Если взять число «минус единица», то его по формуле (5) можно представить как
(10)
то есть комплексным числом, имеющим модуль «единица» и фазу «180 градусов» («пи»).

Таким образом, трёхточечный симметричный алгоритм (1) для некоторых «высоких» частот вносит сдвиг по фазе на 180 градусов, то есть попросту инвертирует входной сигнал. Этот эффект можно заметить, анализируя рассмотренный выше отклик на нормированную частоту 2/5 Гц.

Рис. 1. Амплитудно-частотная и фазо-частотная характеристики трёхточечного симметричного алгоритма сглаживания (1)

Из рис. 1 сразу следует, что сигнал с частотой 1/3 будет данным алгоритмом подавлен, а сигналы, имеющие частоту выше 1/3 будут инвертированы. Таким образом, полезный рабочий диапазон частот можно смело сократить с [0…0,5] до [0…1/3]. Если нас не устраивает быстрое спадание коэффициента передачи, придётся определять другой алгоритм, имеющий более прямоугольную амплитудно-частотную характеристику и при этом — ещё неизвестно какую фазовую…

По сути, полученная немонотонная частотная характеристика — следствие прямоугольной формы импульсной характеристики …, 0, 0, …, 1/3, 1/3, 1/3, 0, 0, …. Поэтому импульсная характеристика — простой способ заметить грубые изъяны в алгоритмах. Частотная характеристика, несмотря на некоторую сложность её вычисления, удобна тем, что позволяет заметить и устранить более тонкие изъяны, чем мы и займёмся.

Если теперь записать алгоритм (1) в более общем виде
(11)
то, основываясь на знании частотной характеристики, можно попытаться подобрать коэффициенты так,
чтобы амплитудно-частотная характеристика стала монотонной в рабочем диапазоне частот (0…0,5). Для этого, как минимум, необходимо отсутствие нулей внутри рабочего диапазона.

Так как у нас нет оснований выделять запаздывающий отсчёт s[i–1] по отношению к опережающему s[i+1], то приравняем коэффициенты a₁ и a₃. После запишем коэффициент передачи
(12)

Попытаемся переместить первый нуль на частоту f₀ = 0,5. Для этого должно выполняться равенство a₂ = 2a₁ , то есть вес у боковых отсчётов должен быть в два раза меньше веса центрального. Тогда более оптимальный алгоритм будет выглядеть так
(13)

Как в (13) выбрать единственный коэффициент a₁?

Взглянем на алгоритм (13) с точки зрения импульсной переходной характеристики. Для этого найдём отклик на единичный скачок :
(14)

Как видим, чтобы сохранить выходную амплитуду в установившемся режиме, равную единице, требуется выбрать коэффициент a₁=1/4. То есть сумма всех коэффициентов должна быть равна единице.

Наконец, для готового алгоритма
(16)
можно построить (рис. 2) частотные характеристики: амплитудную и фазовую.

Рис. 2. Амплитудно-частотная и фазо-частотная характеристики трёхточечного симметричного алгоритма сглаживания (16)

Анализ рис. 2 показывает, что фазовые искажения исчезли, а амплитудная характеристика стала монотонной в рабочей полосе частот [0…0,5]. В каком-то смысле мы выжали из трёхточечного фильтра «всё».

Теперь становится очевидно, что простое усреднение далеко не всегда является оптимальным, особенно когда усредняемых отсчётов много.

Изображения

Что касается изображений, то здесь в какой-то мере всё то же самое, что и для сигналов: амплитудные и фазовые искажения, импульсные характеристики, энергия сигнала, — основное отличие заключается в том, что используются матрицы вместо векторов. Также следует учесть, что для изображений нет координаты времени, а есть координата пространства, поэтому есть пространственные частоты дискретизации. Данное отличие скорее формальное, так как на математику алгоритмов оно не влияет вообще.

Рассмотрим теперь «самый простой» алгоритм сглаживания изображения по соседним точкам (рис. 3). Отсчёт v₀₀ на выходе фильтра
(17)

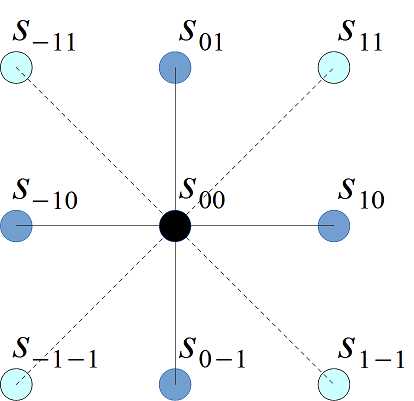
Рис. 3. Схема сглаживания изображения по соседним точкам

В формуле (17) специально выделены три слагаемых A, B и C, так как четыре соответствующих внутренних слагаемых у B и C имеют свои расстояния от центрального отсчёта s₀₀. Здесь естественно предположить, что максимальный вес будет у слагаемого A, затем в порядке убывания — у B и C.

Для изображений спектр и коэффициент передачи будут двумерными, то есть будут зависеть от двух частот: первая частота — по горизонтали, вторая — по вертикали (здесь всё условно, для определённости).

Фильтр (17) имеет следующий коэффициент передачи
(18)

Если взять, например, около тридцати дискретных частот и построить (рис. 4) контурный график модуля частотной характеристики (18), то можно увидеть искажения, аналогичные искажениям на рис. 1. Левому нижнему углу соответствуют самые низкие частоты. Наблюдается провал частотной характеристики на частотах, составляющих 1/3 от частоты дискретизации (частоты дискретизации в данном случае равны 64 по обеим координатам).

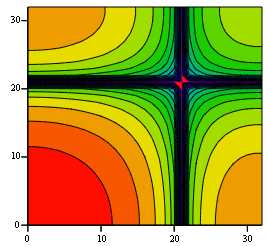
Рис. 4. Амплитудно-частотная характеристика девятиточечного симметричного алгоритма сглаживания (17)

Перетасовывая коэффициенты для отсчётов на рис. 3, можно получить следующий алгоритм сглаживания
(19)

Причём если единичное воздействие поместить в центре изображения, то отклик фильтра (19) будет иметь вид
(20)

По сути, (20) является импульсной характеристикой фильтра (это девять главных отсчётов, так как остальные равны нулю). Сумма всех отсчётов импульсной характеристики равна единице. Частотная характеристика фильтра (19) имеет вид, показанный на рис. 5.

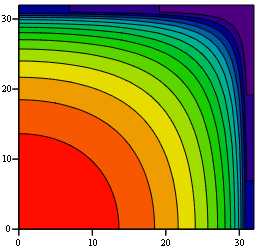
Рис. 5. Амплитудно-частотная характеристика девятиточечного симметричного алгоритма сглаживания (19)

Опять мы видим (сравни рис. 4 и рис. 5) улучшение алгоритма обычного усреднения.

Резюме

При разработке алгоритмов обработки цифровых сигналов (сглаживания и не только) не следует доверять интуитивным алгоритмам вроде простого усреднения.

Более общим подходом является техника весового суммирования (рассматривались только линейные алгоритмы, когда отсчёты только лишь умножаются на константы, а результаты — складываются).

Весовое суммирование, когда более отдалённым от центрального элемента отсчётам ставятся меньшие веса, оправдано как статистически (естественная природа ослабления зависимости с ростом расстояния), так и функционально (возможно строго математически подобрать коэффициенты, обеспечив монотонность амплитудно-частотной характеристики).

Большую роль играют амплитудно-частотные характеристики фильтров, которые определяются коэффициентами весового суммирования. Они позволяют доказать, что заданный фильтр пропускает определённый диапазон частот и заграждает другой. Причём можно определить неравномерность в полосе пропускания, в полосе заграждения и так далее. Чем больше порядок фильтра, тем больше степеней свободы и тем лучше можно подобрать форму амплитудно-частотной характеристики.

Важную роль играют и фазо-частотные характеристики, которые, в основном, определяются степенью симметричности алгоритма. Алгоритмы реального времени, когда в момент прихода первого отсчёта появляется отсчёт на выходе фильтра, не могут обеспечить равномерную фазовую характеристику (константу, чаще всего «нуль»), так как они не могут быть симметричными. Такие алгоритмы вносят задержку во входной сигнал: например, сглаженное изображение может в целом сместиться по обеим координатам. Если изображение сложное (то есть имеет много частотных составляющих), то фазовые искажения его могут заметно исказить, а не просто сместить по координатам, что приближённо справедливо для простых изображений.

Также следует обратить внимание на импульсную характеристику фильтра, соответствующего некоторому алгоритму. Это позволяет простым способом взглянуть на работу фильтра напрямую, то есть в масштабе времени для сигнала или в масштабе пространственных координат — для изображения.

И, наконец, необходим энергетический анализ алгоритма, позволяющий определить потери сигнала на выходе соответствующего фильтра. Данный анализ удобно провести в рамках импульсной переходной характеристики.

Сноски

1. Всегда с потерями, так как частота работы и разрядность цифровых устройств ограничены
2. Стабилизирующее свойство средней величины справедливо при неизменности характеристик генератора случайных чисел, то есть в идеале генератор должен выдавать случайную величину с заданным законом распределения
3. Если, конечно, наблюдаемый шум — это не зашифрованный полезный сигнал, который становится случайным для тех, кто не имеет ключа…
4. Для звукового сигнала расстояние между отсчётами — это некоторый промежуток времени
5. Можно считать, что любой сигнал можно представить в виде суммы синусоид кратных частот, но звуковой по природе обязан «хорошо» раскладываться в ряд по частотам
6. Упрощённо можно сказать и так, подробности смотри ниже по тексту

Источники

1. Тригонометрические функции [Электронный ресурс], режим доступа: свободный, ru.wikipedia.org/wiki/%D2%F0%E8%E3%EE%ED%EE%EC%E5%F2%F0%E8%F7%E5%F1%EA%E8%E5_%F4%F3%ED%EA%F6%E8%E8
2. Экспонента [Электронный ресурс], режим доступа: свободный, ru.wikipedia.org/wiki/%DD%EA%F1%EF%EE%ED%E5%ED%F2%E0

habr.com

Цифровая обработка сигналов

10

Тема 3. Фильтры сглаживания. Метод наименьших квадратов.

Не перестаю удивляться дерзкой гениальности Стефенсона и братьев Черепановых. Как они отважились построить паровоз, не располагая теорией его движения?

Архив Кифы Васильевича. Наука и жизнь, 1984.

Пока нет теории, есть возможность войти в Историю. Бог прославился созданием Евы из ребра Адама без всякого теоретического обоснования. А когда теория есть, можно только влипнуть в какую-нибудь историю.

Лариса Ратушная. Уральский геофизик, XX в.

Содержание

Введение.

1. Фильтры МНК 1-го порядка. Расчет коэффициентов фильтра. Импульсная реакция фильтра. Частотная характеристика фильтра. Модификация фильтра. Оптимизация сглаживания. Последовательная фильтрация.

2. Фильтры МНК 2-го порядка. Расчет фильтров. Частотные характеристики фильтров. Модификация фильтров. Последовательная фильтрация.

3. Фильтры МНК 4-го порядка.

4. Расчет простого цифрового фильтра по частотной характеристике.

Введение

Основной инструмент цифровой фильтрации данных и проектирования цифровых фильтров – спектральный (частотный) анализ. Частотный анализ базируется на использовании периодических функций, в отличие от численных методов анализа и математической статистики, где предпочтение отдается полиномам. В качестве периодических используются гармонические функции синусов и косинусов. Спектральный состав сигналов – это тонкая внутренняя структура данных, которая практически скрыта в динамическом представлении данных даже для опытных обработчиков. Частотная характеристика цифрового фильтра – это его однозначный функциональный паспорт, полностью определяющий сущность преобразования входных данных.

Следует отметить, что хотя цель фильтрации сигналов состоит именно в направленном изменении частотного состава данных, которые несет сигнал, у начинающих специалистов существует определенное эмоциональное противодействие частотному подходу в анализе данных. Преодолеть это противодействие можно только одним путем – на опыте убедиться в эффективности частотного подхода.

Рассмотрим пример частотного анализа фильтров при сглаживании данных методом наименьших квадратов (МНК).

3.1. Фильтры мнк 1-го порядка [24].

Предположим, что требуется осуществить сглаживание (аппроксимацию) равномерного по аргументу массива данных методом наименьших квадратов (МНК).

Расчет коэффициентов фильтра. Простейший способ аппроксимации по МНК произвольной функции s(t) — с помощью полинома первой степени, т.е. функции вида y(t) = A+Bt (метод скользящих средних). Произведем расчет симметричного фильтра МНК на (2N+1) точек с окном от -N до N.

Для определения коэффициентов полинома найдем минимум функции остаточных ошибок приближения. С учетом дискретности данных по точкам t_n= nt и принимая t = 1, для симметричного НЦФ с нумерацией отсчетов по n от центра окна фильтра (в системе координат фильтра), функция остаточных ошибок записывается в форме:

(A, B) = 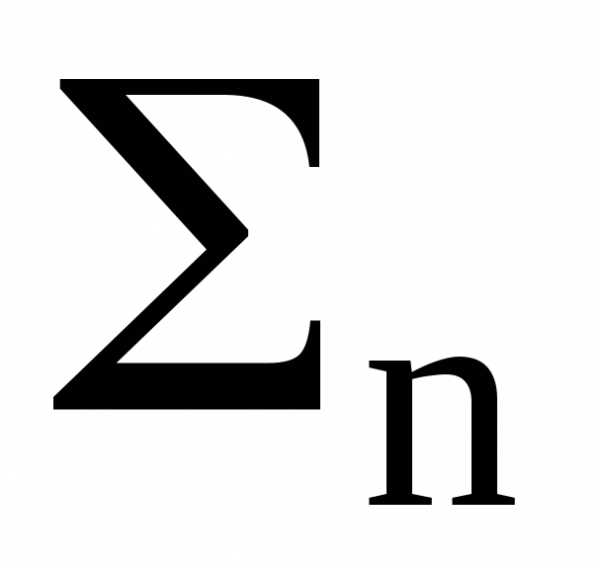[s_n — (A+B·n)]².

Дифференцируем функцию остаточных ошибок по аргументам А, В, и, приравнивая полученные уравнения нулю, формируем 2 нормальных уравнения с двумя неизвестными:

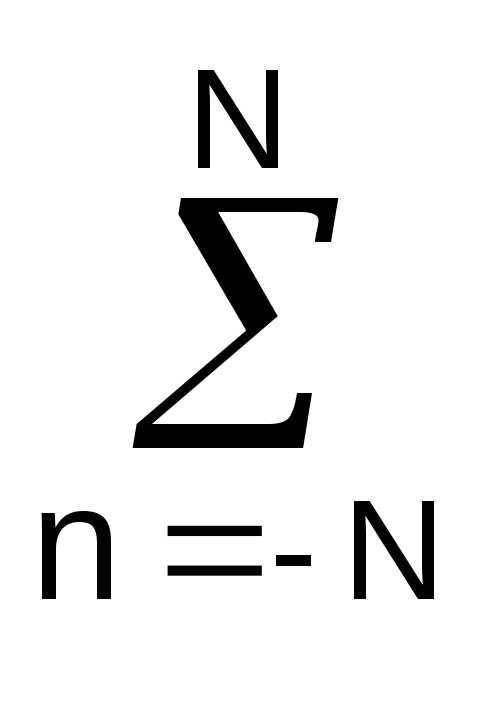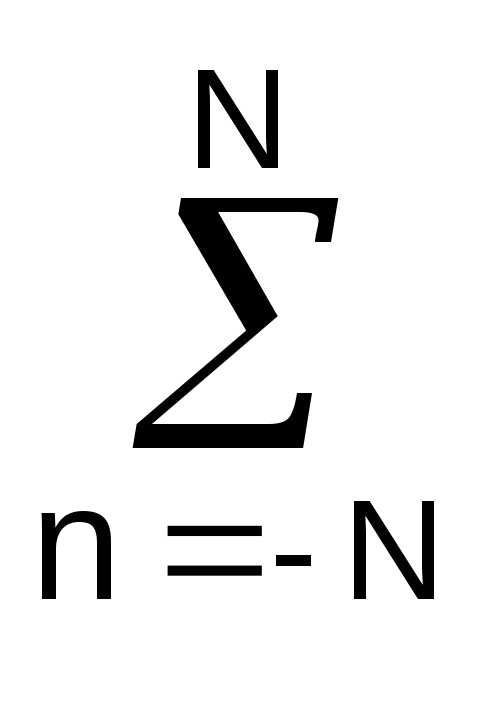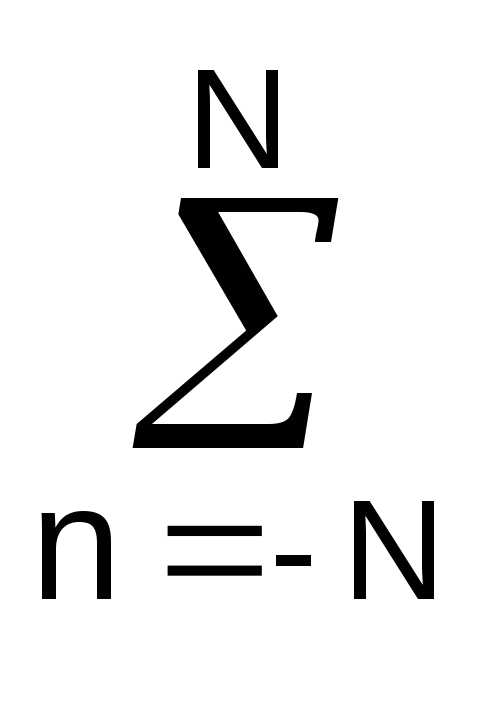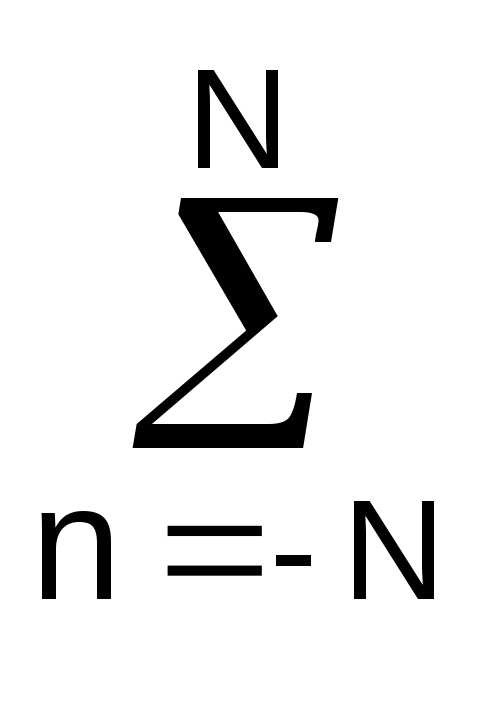(s_n-(A+B·n)) s_n — A1 — Bn = 0,

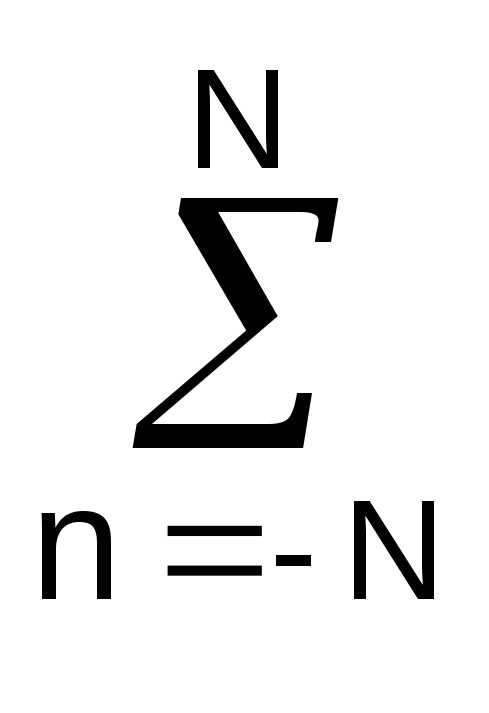(s_n-(A+B·n))·n 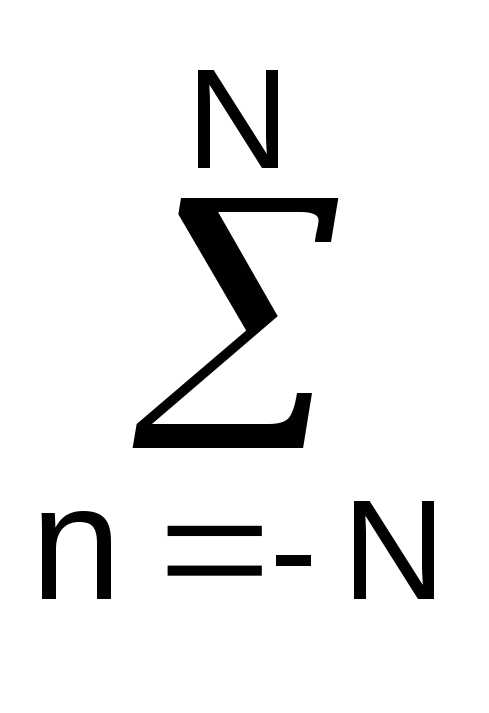ns_n — A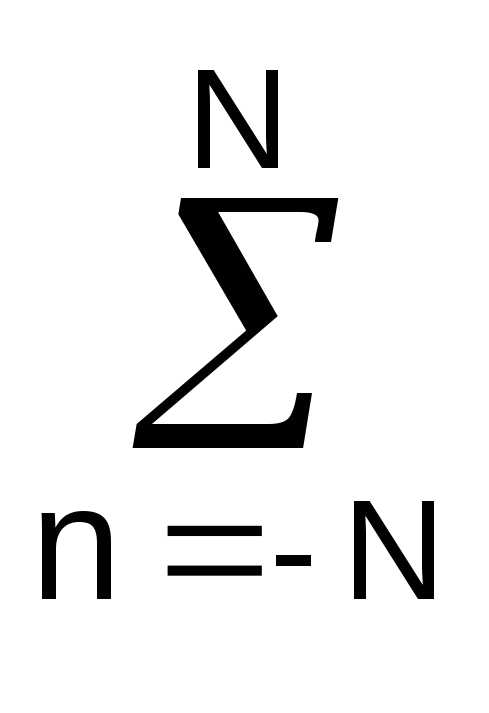n — B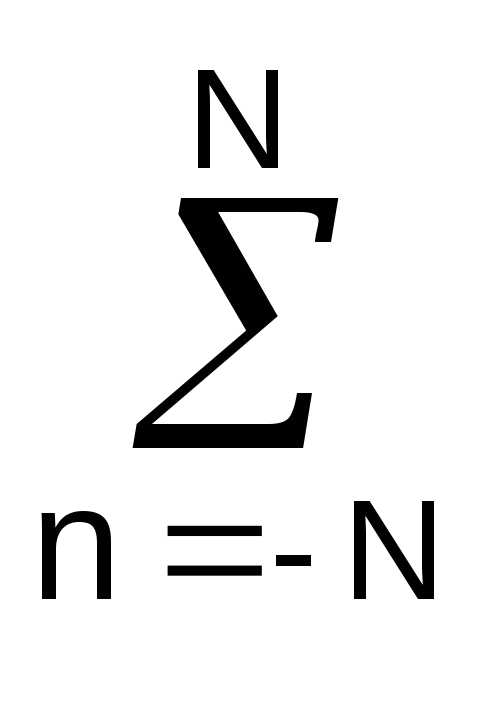n² = 0.

С учетом равенства 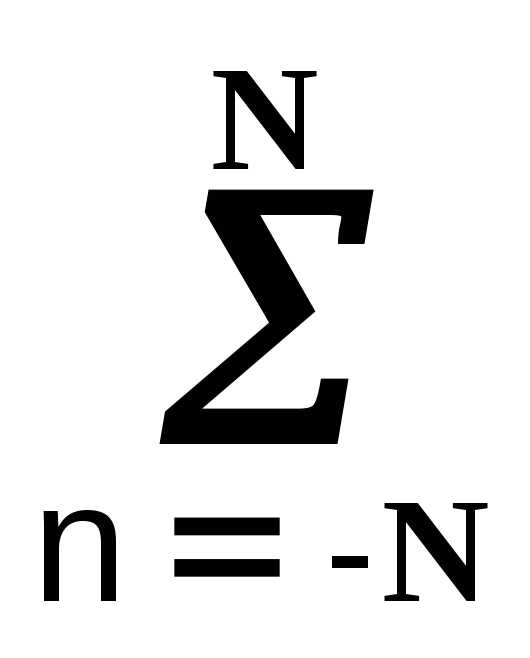n = 0, решение данных уравнений относительно А и В:

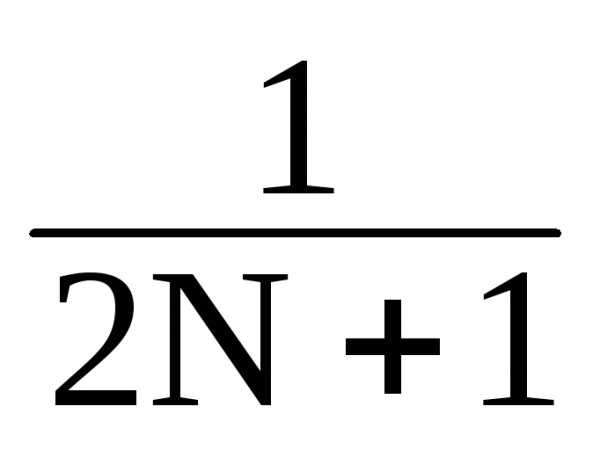
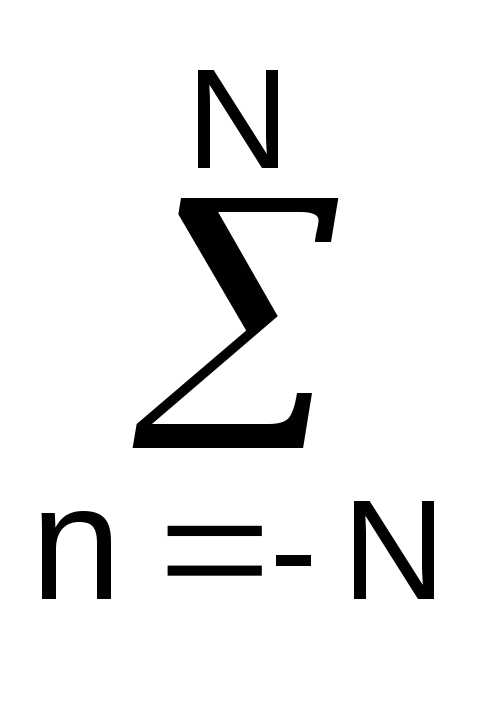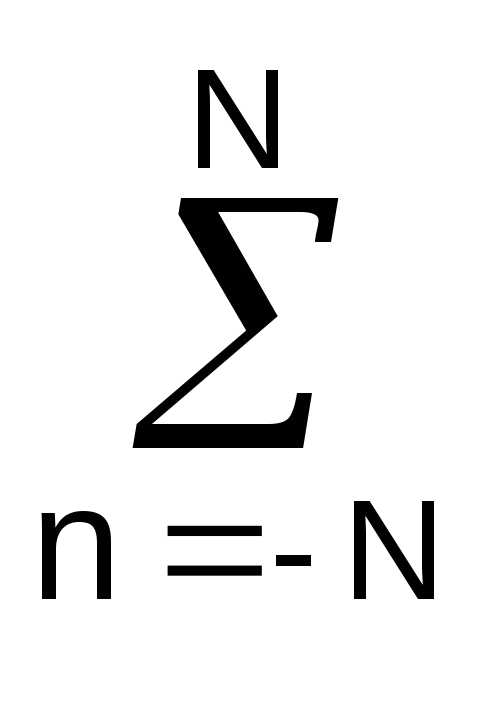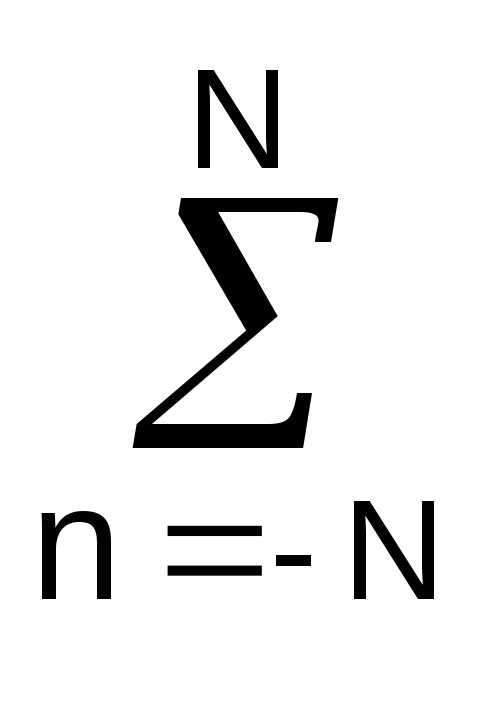А = s_n, B =ns_n/n².

Подставляем значения коэффициентов в уравнение аппроксимирующего полинома, переходим в систему координат по точкам k массива y(k+) = A+B·, где отсчет  производится от точки k массива, против которой находится точка n = 0 фильтра, и получаем в общей форме уравнение фильтра аппроксимации:

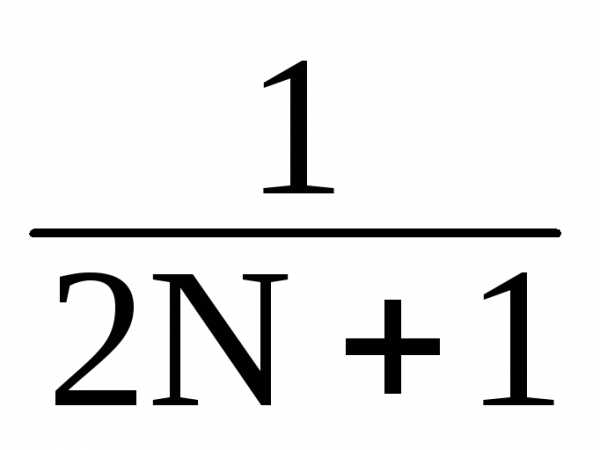
y(k+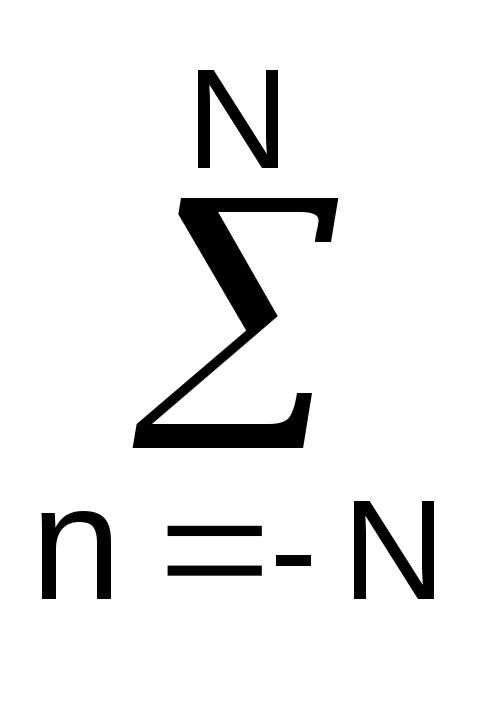) = s_k-n + 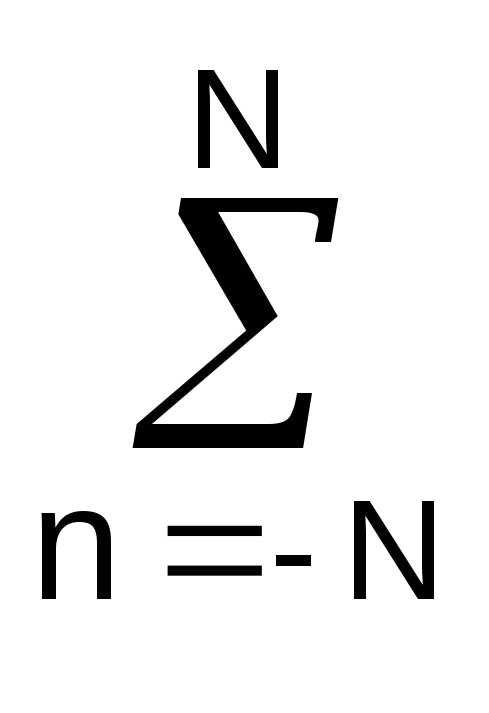ns_k-n/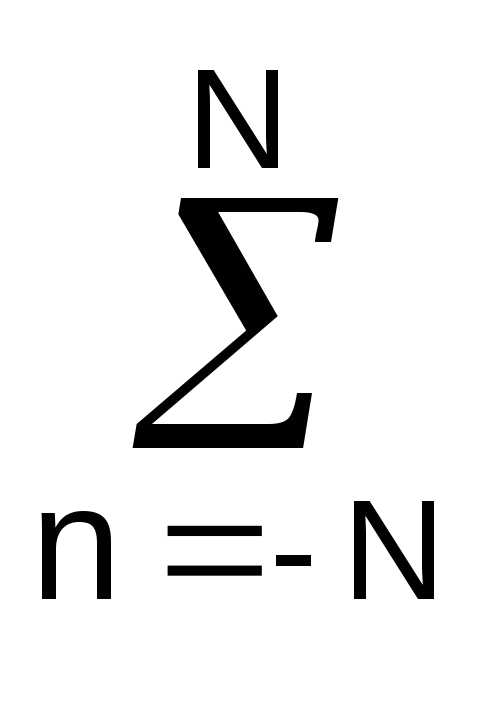n².

Для сглаживающего НЦФ вычисления производятся непосредственно для точки k в центре окна фильтра (= 0), при этом:

y_k =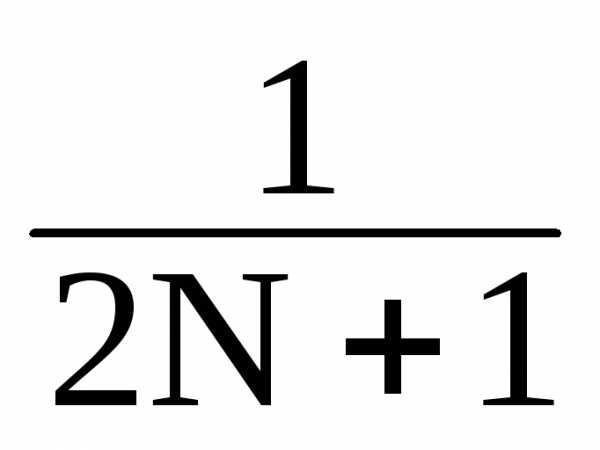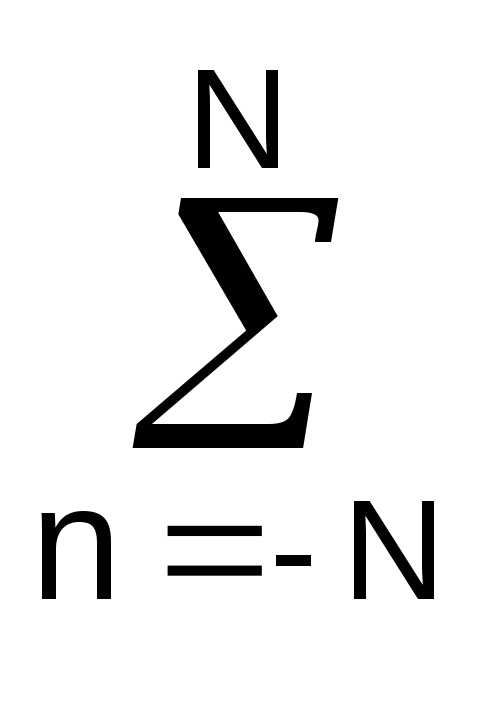s_k-n. (3.1.1)

Рис. 3.1.1.

Импульсная реакция фильтра соответственно определяется (2N+1) значениями коэффициентов b_n = 1/(2N+1). Так, для 5-ти точечного НЦФ:

h(n) = {0.2, 0.2, 0.2, 0.2, 0.2}.

Передаточная функция фильтра в z-области:

H(z) = 0.2(z^-2+z^-1+1+z¹+z²).

Коэффициент усиления дисперсии шумов:

K_q=_nh²(n) = 1/(2N+1),

т.е. обратно пропорционален ширине окна фильтра. Зависимость значения K_q от ширины окна приведена на рис. 3.1.1.

Частотная характеристика фильтра (передаточная функция фильтра в частотной области) находится преобразованием Фурье импульсной реакции h(n) (фильтр симметричный, начало координат в центре фильтра), или подстановкой z = exp(-jt) при t=1 в выражение передаточной функции H(z). И в том, и в другом случае получаем:

H() = 0.2[exp(2j)+exp(j)+1+exp(-j)+exp(-2j)]. (3.1.2)

Можно использовать и непосредственно уравнение фильтра (3.1.1). Подадим на вход фильтра гармонический сигнал вида s_k = exp(jk). Так как сигнальная функция относится к числу собственных, на выходе фильтра будем иметь сигнал y_k = H()exp(jk). Подставляя выражения входного и выходного сигналов в уравнение (3.1.1), получаем:

H() exp(jk) = 0.2exp(j(k-n))= 0.2 exp(jk)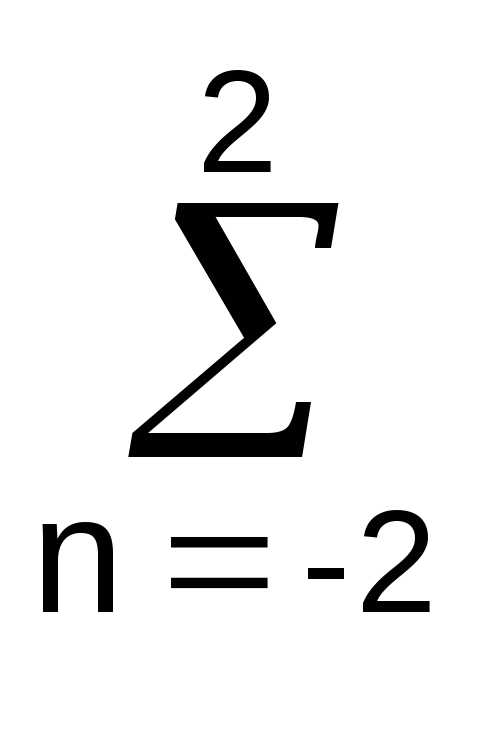exp(-jn).

Отсюда, выражение для передаточной функции:

H() = 0.2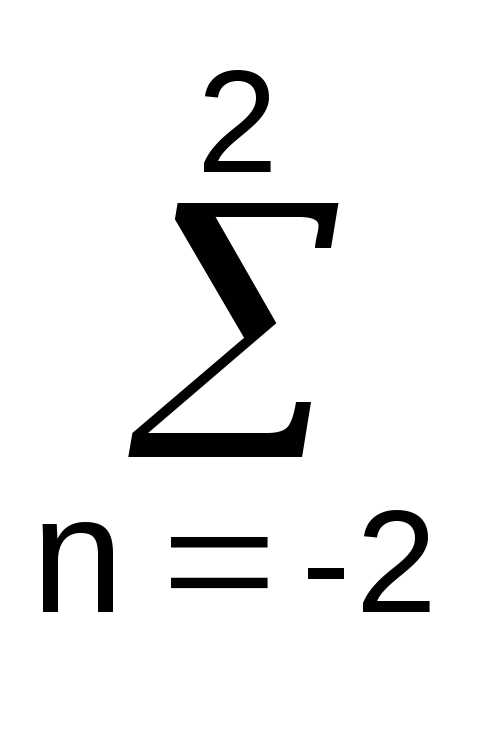exp(-jn) = 0.2[exp(2j)+exp(j)+1+exp(-j)+exp(-2j)],

что полностью идентично выражению (3.1.2).

Так как импульсная реакция фильтра МНК симметрична (функция h(n) четная), частотное представление передаточной функции должно быть вещественным, в чем нетрудно убедиться, объединив комплексно сопряженные члены выражения (3.1.2):

H() = 0.2(1+2 cos+2 cos 2).

Альтернативное представление передаточной функции H() фильтра с произвольным количеством коэффициентов 2N+1 достаточно хорошо известно, как нормированный фурье-образ прямоугольной функции, каковой по существу и является селектирующее окно фильтра (3.1.1):

H() = sin((N+1/2))/[(N+1/2)] = sinc((N+1/2)). (3.1.3)

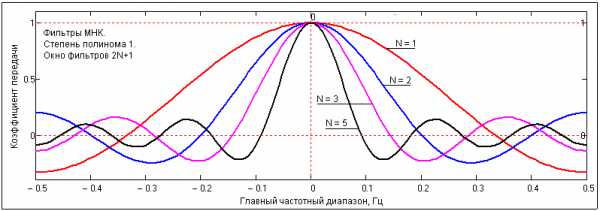
Рис. 3.1.2. Частотные характеристики фильтров МНК-1.

Графики передаточных функций (3.1.3) приведены на рисунке 3.1.2. По графикам можно видеть коэффициент передачи сигнала с входа на выход фильтра на любой частоте в главном частотном диапазоне. Без ослабления (с коэффициентом передачи 1) сглаживающим фильтром пропускается только сигнал постоянного уровня (нулевой частоты). Сумма коэффициентов сглаживающего НЦФ всегда должна быть равна 1 (отсчет дискретного фурье-преобразования на частоте  = 0 равен сумме значений входной функции).

Чем больше число коэффициентов фильтра (шире окно фильтра), тем уже полоса пропускания низких частот. Подавление высоких частот довольно неравномерное, с осцилляциями передаточной функции относительно нуля. На рис. 3.1.3 приведен пример фильтрации случайного сигнала (шума) фильтрами с разным размером окна.

Рис. 3.1.3. Фильтрация шумов фильтрами МНК 1-го порядка.

Рис. 3.1.4.

Модификация фильтра. Частотное представление передаточных функций позволяет наглядно видеть особенности фильтров и целенаправленно улучшать их характеристики. Так, если в рассмотренном нами фильтре с однородной импульсной реакцией h_n = 1/(2N+1) уменьшить два крайних члена в 2 раза и заново нормировать к сумме h_n = 1, то частотные характеристики фильтра заметно улучшаются. Для нахождения передаточной функции модифицированного фильтра снимем в выражении (3.1.3) нормировку на 2N+1, вычтем значение 1/2 крайних членов (exp(-jN)+exp(jN))/2 = cos N и заново пронормируем полученное выражение к 1 (разделим на 2N). Пример новой передаточной функции при N=3 приведен на рисунке 3.1.4. Передаточные функции модифицированных таким образом фильтров приводятся к нулю на частоте Найквиста, при этом несколько расширяется полоса пропускания низких частот и уменьшается амплитуда осцилляций в области подавления высоких частот. Если смотреть на сглаживание, как на операцию подавления высокочастотных помех, то модифицированные фильтры больше соответствует своему назначению.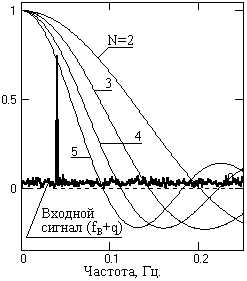

Рис. 3.1.5.

Оптимизация сглаживания. При выборе окна фильтра следует учитывать как коэффициент подавления дисперсии шумов, так и степень искажения полезного сигнала, на который наложены шумы. Оптимальное окно фильтра может быть определено только в том случае, если спектр сигнала известен и ограничен определенной верхней частотой, а мощность шумов не превышает определенного уровня. Рассмотрим это на конкретном примере.

Допустим, что нужно обеспечить максимальное подавление дисперсии шумов при минимальном искажении верхней граничной частоты сигнала f_в, при этом мощность шумов равна мощности гармоники f_в. Допустим, что значение f_в равно 0.08 частоты Найквиста данных, т.е. f_в = 0.04 Гц при t=1. Мощности гармоники и шума принимаем равными 1. Спектр модели сигнала плюс шума в сопоставлении с передаточными функциями фильтров приведен на рис. 3.1.5.

Таблица 3.1.1.

N	0	1	2	3	4	5	6	7
Ку(fв)	1	0.98	0.94	0.88	0.8	0.7	0.6	0.51
Wu(N)	1	0.96	0.88	0.77	0.64	0.51	0.38	0.26
Wq(N)	1	0.33	0.2	0.14	0.11	0.09	0.08	0.07
Кс/ш	1	2.88	4.4	5.4	5.8	5.6	4.89	3.85
	1	0.35	0.23	0.18	0.17	0.18	0.21	0.26
	1	0.32	0.2	0.15	0.15	0.18	0.23	0.31

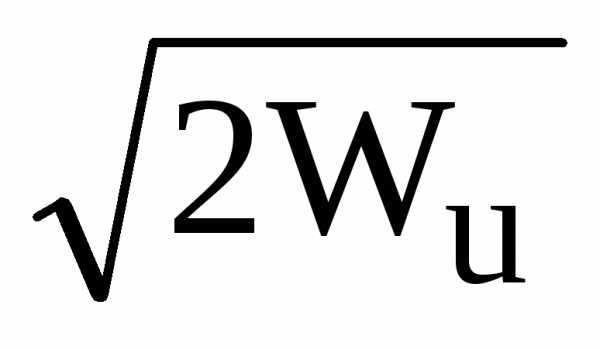По формуле (3.1.3) вычисляем коэффициенты К_у(f_в) усиления фильтров с N от 0 до 7 на частоте f_в (см. таблицу 3.1.1). При мощности гармоники W_u = 1 амплитудное значение гармоники на входе фильтра равно U = = 1.41. Мощности гармоник на выходе фильтров в зависимости от N:

Рис. 3.1.6.

W_u(N)= 0.5·[U· К_у(f_в)]².

Соответственно, при мощности входного шума W_q=1 мощности шумов на выходе фильтров будут численно равныкоэффициентам усиления дисперсии шумов W_q(N) = W_q·K_q(N).

Максимум отношения

К_с/ш  W_u(N)/W_q(N)

определяет оптимальный фильтр с максимальным увеличением отношения сигнал/шум, т.е., по существу, коэффициент увеличения отношения сигнал/шум при выполнении фильтрации с учетом изменения амплитудных значений полезной части сигнала на выходе фильтра.

Рис. 3.1.7.

При К_у(f_в) > 0.5 и W_u(N) = W_q(N) = 1 численные значения величины ^ = 1/ К_с/ш в первом приближении могут служить оценкой ^ квадрата среднего квадратического отклонения выходных сигналов от «чистой» гармоники f_в, заданной на входе. Свидетельством этому служат последние строки таблицы 3.1.1, где приведены результаты математического моделирования фильтрации по данным условиям на выборке 10000 точек. На рис. 3.1.7 приведены результаты сопоставления расчетных ^ и модельных ^ значений данных коэффициентов.

Пример фильтрации зашумленного входного сигнала с полезной частотой f_в = 0.04 Гц (синий пунктир) оптимальным фильтром МНК для данных условий (N=3) приведен на рис. 3.1.8.

Рис. 3.1.8.

Последовательная фильтрация. Из фильтров МНК можно конструировать новые фильтры, частотные характеристики которых соответствуют последовательному применению «родительских» фильтров. Это выполняется последовательной n-кратной сверткой оператора исходного фильтра с самим собой, что дает эквивалент операторов n-кратной последовательной свертки данных с «родительским» оператором. Обычно применяется одно- и двукратная свертка, при этом окно нового фильтра расширяется, полоса пропускания по уровню 0.5 уменьшается (примерно на 25 и 40% соответственно), но резко уменьшается амплитуда пульсаций в зоне подавления (примерно в 4 и 16 раз соответственно). Пример конструирования новых фильтров из 7-ми точечного фильтра МНК-1 и их частотных характеристик приведен на рис. 3.1.9.

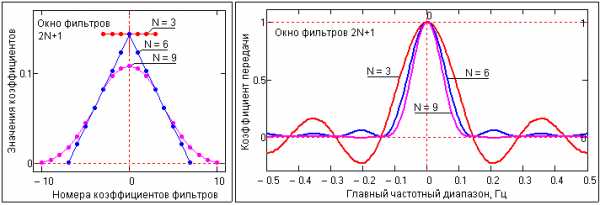
Рис. 3.1.9.

studfiles.net

Simatic Step 7, STL, сглаживание (Smooth) сигнала аналогового входа 4-20mA.

  Simatic это абревиатура семейств PLC фирмы Siemens для общепромышленного применения (SIMATIC S7-300/S7-400/C7/WinAC). Сейчас есть и более новые SIMATIC S7-1200/S7-1500, программируются через TIA Portal.
  Siemens выпускает и узко специализированные линейки PLC (Sinumerik — для станков ЧПУ, Simadyn — линейка повышенной производительности, многие задачи решаются аппаратно, специализированными блоками). Так же широко распостранены абревиатуры, которые относятся к области применения, а не к линейке аппаратного обеспечения на котором оно собрано, естественно оно должно поддерживать стандарты фирмы Siemens (SIMATIC HMI — управление оборудованием с панели оператора, SIMATIС NET — все что связано с межблоковой связью, SIMOTION — моторизованные приводы, управляющие движением, SIMODRIVE — инверторы, управляемые через ProfiBus, и еще куча абревиатур на которые Siemens имеет товарные знаки).
  Step 7 это IDE для программирования всего этого хозяйства (кроме устаревшего S7-200, для него используется STEP 7-Micro/WIN, несмотря на схожее название, это отдельная программа и в IDE Step 7 не интегрируется). Составить представление можно почитав статью на Хабре Программирование ПЛК Siemens на Simatic Step7. Дополнительные языки программирования, драйвера оборудования и т.д. интегрируются в Step 7. Доступны драйверы для широкой номенклатуры стороннего оборудования (не Siemens).
  Инструментальные средства STEP 7 позволяют выполнять:

Конфигурирование и определение параметров настройки аппаратуры;
Конфигурирование систем промышленной связи и настройку параметров передачи данных;
Программирование, тестирование, отладку и запуск программ отдельных систем автоматизации, а также их локальное или дистанционное обслуживание;
Документирование и архивирование данных проекта;
Функции оперативного управления и диагностирования аппаратуры.
  STL — один из МЭК (IEC) стандарта IEC61131-3 языков программирования (англ. Statement List, список операторов). Немцы зовут его AWL (нем. Anweisungsliste), это же расширение имеют и исходники, написанные на STL. Тут есть несоответствие в абревиатурах стандартных языков МЭК и фирмы Siemens. Дело в том, что по стандартам МЭК язык STL должен называться IL (Instruction List), а абревиатура ST (Structured Text) зарезервирована за Pascal-подобным языком, который у Siemens называется SCL (Structured Control Language).
  Кроме STL, Step 7 включает в дистрибутив поддержку МЭК языков LAD (Ladder Diagram, язык релейной (лестничной) логики) и FBD (Function Block Diagram, программирование функциональными блоками). При приобретении лицензии интегрируются языки SCL (Pascal-подобный язык), S7-GRAPH (позволяет выполнять конфигурирование и программирование систем графическими способами, стандарт DIN EN 6.1131-3), S7-HiGraph (позволяет разрабатывать программы систем автоматизации SIMATIC в виде графа состояния системы), S7-PDIAG (позволяет разрабатывать однородные процедуры диагностирования систем автоматизации SIMATIC), S7-PLCSIM (позволяет эмулировать работу систем автоматизации SIMATIC, предназначен для отладки программ указанных систем на программаторе/компьютере без использования реальных технических средств автоматизации).
  В настоящее время Siemens активно рекомендует переходить со Step 7 на TIA Portal. Это логическое развитие Step 7, но не всегда однозначное (IMXO, что-то теряем, что-то находим…).
  Представленный функциональный блок выполняет функции ограничителя аналогового сигнала (4..20mA) с индикацией выхода за диапазон (Limiter) и его сглаживания по алгоритму простого (арифметического) скользящего среднего (SMA).
  Алгоритмов скользящего среднего несколько, SMA (простой, Simple Moving Average), EMA (экспоненциальный, Exponential Moving Average), WMA (взвешенный, Weighted Moving Average). Последние еще и разновидности имеют. Здесь рассмотрен только первый.

  Код функционального блока был написан для контроллера семейства Simatic S7-300, конкретно для S7-313C.
  Как правило (за редким исключением, S7-313C как раз из них), входные аналоговые модули S7-300 имеют универсальные входы. У ранних ревизий переключателем на боковой стенке модуля можно перевести вход в режим работы с сигналами напряжения, тока, термометров сопротивления и резисторов, термопар (4 положения). Аналоговые модули не имеющие переключателя (новые ревизии), конфигурируются утилитой Hardware Configuration, входящей в состав пакета STEP7.
  Здесь рассмотрена работа с аналоговым входом, настроенным на измерение тока 4-20mA. Он преобразует входной ток в слово (16-разрядное HEX число).



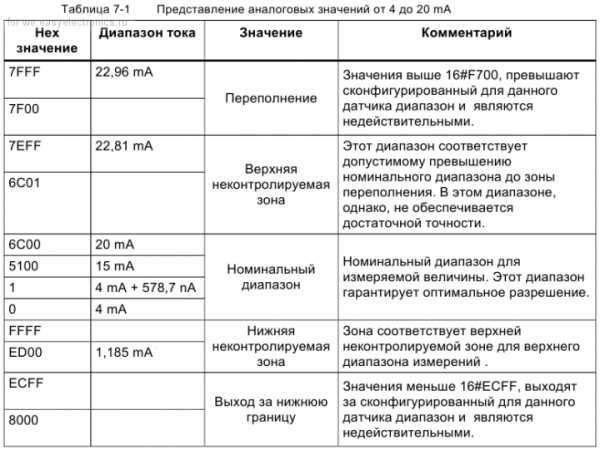
  У различных модулей аналоговых входов Simatic разрешающая способность может быть от 9 до 15 бит + знак. Если разрешающая способность аналогового модуля составляет менее 16 бит, то аналоговая величина сохраняется в модуле с выравниванием влево. Младшие, не используемые, битовые разряды заполняются нулями.
  Из таблицы видно, что модуль с состоянии работать с входным током в диапазоне 1,185mA — 22,81mA. Ток не входящий в данный диапазон вызывает переполнение и показания являются недействительными. Нередкие в промышленности отказ датчика или обрыв провода приведут к выходу измеряемого тока из диапазона работы аналогового входа.
  Поэтому перед любой обработкой полученных данных от аналогового входа необходимо их нормализовать, т.е. отсечь недействительные значения. Один из вариантов такой функции на языке STL:


FUNCTION FC20: VOID	

TITLE = Ограничитель аналового сигнала 4-20mA

AUTHOR:   Anakost  
FAMILY:   SOHO	   
NAME:     LIMITER   
VERSION:  1.0	   

VAR_INPUT            
  INPUT: INT;	// входной ток
END_VAR

VAR_OUTPUT            
  OUTPUT: INT;	// выходной ток
  RANGE: BOOL;	// выход за диапазон   
END_VAR

BEGIN

NETWORK
TITLE = Ограничение аналогового сигнала

  L #INPUT;	// ACCU 1 <- INPUT, входной ток	
  L W#16#6C00;	// ACCU 1 <- константа 20mA, ACCU 2 <- ACCU 1
  >I;		// в RLO результат сравнения ACCU 2 > ACCU 1
  = #RANGE;	// RANGE <- RLO	   
  JC A00;	// в ACCU 1 верхняя граница диапазона
  L #INPUT;	// ACCU 1 <- INPUT, входной ток
  L W#16#0;	// константа 4mA
  <I;		// в RLO результат сравнения ACCU 2 < ACCU 1   
  = #RANGE;	// RANGE <- RLO	   
  JC A00;	// в ACCU 1 нижняя граница диапазона
  L #INPUT;	// ACCU 1 <- INPUT, входной ток
A00:
  T #OUTPUT;	// OUTPUT <- ACCU 1, результат на выход
	
END_FUNCTION


  Небольшое обьяснение к коду для тех, кто незнаком с промышленными контроллерами Siemens. Simatic S7-300 имеет два 32-х разрядных аккумулятора. При загрузке в первый, его предыдущее содержимое сдвигается во второй. Поэтому применение операции сравнения или математической операции требует двух предварительных операций загрузки. Результат сохраняется в первом аккумуляторе. Бит RLO — результат логической операции, применим и для операций сравнения. JC — переход при RLO=1, JCN — переход при RLO=0. W#16#6C00 расшифровывается как шестнадцатиричное (#16) представление слова (W) 6C00, его можно записать и в десятичном виде W#27648 или просто 27648.
  Ограничитель можно оформить в виде функции, т.к. статичной памяти для работы ему не требуется.
  Алгоритм же вычисления арифметического плавающего среднего должен хранить в статичной памяти результаты последних замеров (кольцевой буфер), указатель на последний замер и сумму замеров в буфере. Т.е. иметь статичную память, неизменную между вызовами функции. В Step 7 этим требованиям отвечает функциональный блок. Помимо функции он имеет жестко ассоциированный (экземплярный) блок данных для расчетов. Обращаться к этим данным изнутри функционального блока проще чем к глобальным. Доступ снаружи (не из функционального блока) запрещен и блокируется.
  На рисунке ниже представлена реакция функции простого скользящего среднего на скачок сигнала полного диапазона при буфере в 16 слов, функциональный блок вызывается из блока циклического прерывания ОВ35 с цикличностью 100mc.



FUNCTION_BLOCK FB30

TITLE =  Функция простого скользящего среднего

AUTHOR:   Anakost	//
FAMILY:   SOHO		//
NAME:     LIM_SMA	// Limiter + Simple Moving Average
VERSION:  1.0		//

VAR_INPUT
  INPUT: INT;		// входной ток (Iin)
END_VAR

VAR_OUTPUT
  OUTPUT: INT;		// выходной ток (Iout)
  RANGE: BOOL;		// ошибка диапазона
END_VAR

VAR
  VALUES: ARRAY[0..15] OF INT; // буфер
  STEPER: WORD;		// текущий указатель в буфере
  TOTAL: DWORD;		// сумма значений
END_VAR

VAR_TEMP
  TEMP_VAL: INT;	// временная внутренняя величина
END_VAR

BEGIN

NETWORK
TITLE = Ограничение и сглаживание 4..20mA
// Ограничение
  L #INPUT;		// ACCU 1 <- INPUT, входной ток
  T #TEMP_VAL;		// TEMP_VAL <-ACCU 1, во локальную переменную				
  L W#16#6C00;		// ACCU 1 <- константа 20mA, ACCU 2 <- ACCU 1, верхняя граница диапазона
  >I;			// в RLO результат сравнения ACCU 2 > ACCU 1, проверка на превышение
  = #RANGE;		// RANGE <- RLO
  JC A00;		// в ACCU 1 верхняя граница диапазона
  L #TEMP_VAL;		// ACCU 1 <- INPUT
  L W#16#0;		// ACCU 1 <- константа 4mA, нижняя граница диапазона
  <I;			// в RLO результат сравнения ACCU 2 < ACCU 1, проверка на превышение
  = #RANGE;		// RANGE <- RLO
  JCN A01;		// в ACCU 1 нижняя граница диапазона
A00:
  T #TEMP_VAL;		// TEMP_VAL <- INPUT(Limiter), ограничение входного тока
A01:
// Сглаживание
  L #STEPER;		// ACCU 1 <- STEPER, загрузка текущего указателя
  L P##VALUES;		// ACCU 1 <- @VALUES, загрузка указателя на начало массива
  +D;			// ACCU 1 <-  @VALUES + STEPER, сдвиг начального адреса на адрес слова
  LAR1;			// AR1 <- ACCU 1, регистр-указатель на нужное слово
  POP;			// ACCU 1 <- ACCU 2, ACCU 1 <- STEPER
  + 16;			// ACCU 1 <- STEPER + 16 (длина слова), на следующий адрес
  AW W#16#00FF;		// ACCU 1 <- ACCU 1 AND 00FF, адрес ограничен одним байтом (16х16)
  T #STEPER;		// STEPER <- ACCU 1, сохранить новый адрес
  L #TOTAL;		// ACCU 1 <- TOTAL, загрузить сумму
  L DIW [AR1,P#0.0]; 	// ACCU 1 <- VALUES[STEPER], чтение старого замера
  -D;		   	// ACCU 1 <- TOTAL - VALUES[STEPER], вычтем из суммы
  L #TEMP_VAL;	   	// ACCU 1 <- INPUT(Limiter), новый замер
  T DIW [AR1,P#0.0]; 	// VALUES[STEPER] <- ACCU 1, сохранение в буфере
  +D;		   	// ACCU 1 <- TOTAL + INPUT(Limiter), прибавим к сумме
  T #TOTAL;	   	// TOTAL <- ACCU 1, сохраним новую сумму
  SRD 4;		// ACCU 1 >>>> 4, деление на 16, среднее арифметическое
  T #OUTPUT;		// OUTPUT <- ACCU 1, результат на выход

END_FUNCTION_BLOCK

  Обычно при тестах я пользуюсь симулятором PLCSIM, т.к. не всегда можно собрать стенд, а тем более залезть в работающее оборудование. По словам Siemens PLCSIM позволяет выполнять отладку программы на ранних стадиях разработки проекта и предоставляет следующие преимущества:


• Ускорение отладки программы и снижение затрат на проектирование.
• Повышение качества разрабатываемого программного обеспечения.
И все было ничего, но на этом функциональном блоке PLCSIM меня подвел.
  По рускоязычному мануалу от Siemens второй аккумулятор после математической операции не изменяется. Я этим воспользовался в своем коде, но обнаружил что при запуске под PLCSIM второй аккумулятор обнуляется.

Это привело к тому, что адрес указателя в буфере не изменяется и программа постоянно стоит на первом слове.

Проверил на рабочем S7-300, нет, все работает как и должно быть.

И ревизия PLCSIM у меня вроде не старая (K5.4.5.2), раньше проблем не было, в общем не понял…
  Если хотите, чтобы FB нормально работал и в симуляторе, его нужно немного изменить. Не полагаться на то, что нужное число осталось в ACCU 2, а принудительно загрузить его в ACCU 1. Вырезаем следующие строки:


  POP;			// ACCU 1 <- ACCU 2, ACCU 1 <- STEPER
  + 16;			// ACCU 1 <- STEPER + 16 (длина слова), на следующий адрес
  AW W#16#00FF;		// ACCU 1 <- ACCU 1 AND 00FF, адрес ограничен одним байтом (16х16)
  T #STEPER;		// STEPER <- ACCU 1, сохранить новый адрес


и в самый конец блока (после T #OUTPUT) добавляем:

  L #STEPER;		// ACCU 1 <- STEPER, загрузка текущего указателя
  + 16;			// ACCU 1 <- STEPER + 16 (длина слова), на следующий адрес
  AW W#16#00FF;		// ACCU 1 <- ACCU 1 AND 00FF, адрес ограничен одним байтом (16х16)
  T #STEPER;		// STEPER <- ACCU 1, сохранить новый адрес


  Создавать блоки данных для функциональных блоков вручную нет необходимости и не рекомендуется. Лучше чтобы их создал STEP 7. Для этого нужно в месте вызова функционального блока вызвать его с номером требуемого блока данных. Примерно так:

  CALL FB30, DB30 <Enter>


При этом FB30 должен быть скомпилирован и находиться в папке Blocks, номер блока данных может быть любым, еще не используемым. После нажатия «Enter» STEP 7 предупредит, что данного блока не существует и спросит, надо ли его создать.

При нажатии «Yes» блок данных с необходимой внутренней структурой, правильным TimeStamp (отметка времени) и привязкой к FB30 будет создан:

Вызов блока также дополнится формальными обозначениями входов/выходов:

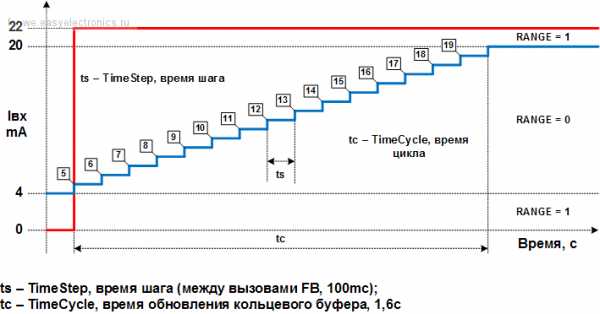
  Блок был опробован на измерении уровня воды в буферном баке (120 м3) датчиком давления. Уровень (0..6м) отслеживается с шагом изменения 0,01м. Ранее при медленном опорожнении бака происходило 4-6 переключений во время смены показаний. После подключения на выход датчика этого функционального блока показания сгладились, происходило 1-2 переключения. Хотелось бы еще плавнее. Это было достигнуто увеличением постоянной времени фильтра. Сделать это несложно, необходимо пропускать некоторые из вызовов фильтра.


  L DB5.Cycle_Counter	// Загрузка счетчика цикла
  LOOP M001		// Декремент и выход если ACCU1 > 0

  CALL FB30, DB30
    INPUT := PIW 754 
    OUTPUT:= MW 112
    RANGE := M 3.4

  L DB5.Division_Factor	// Коэффициент деления 
M001: 
  T DB5.Cycle_Counter	// Сохранение счетчика цикла


Коэффициент деления и счетчик цикла хранятся в глобальном блоке данных. Это сделано для удобной подстройки коэффициента сглаживания во время работы без подключения програматора.

DATA_BLOCK DB5 
 
TITLE = "Параметры сглаживания"
VERSION : 1.0

STRUCT
  Cycle_Counter   : BYTE := B#16#0;	// Счетчик цикла	
  Division_Factor : BYTE := B#16#4;	// Коэффициент деления	
END_STRUCT;

BEGIN
  Division_Factor  := B#16#4;
END_DATA_BLOCK


Коэффициент деления Division_Factor выведен как тег в операционной панели.
  И в заключение расскажу еще об одном эксперименте с этим функциональным блоком. Вход и выход блока имеют одинаковый тип данных. А что если включить два блока цепочкой, один за другим? Чтобы оставить только необходимое, был оформлен новый функциональный блок.

FUNCTION_BLOCK FB40

TITLE = Функция сдвоенного простого скользящего среднего

AUTHOR:   Anakost     	//
FAMILY:   SOHO		//
NAME:     LIM_DSMA	//Limiter + Double Simple Moving Average 
VERSION:  1.0		//

VAR_INPUT            
  INPUT: INT;		// входной ток (Iin)
END_VAR

VAR_OUTPUT            
  OUTPUT: INT;		// выходной ток (Iout)
  RANGE: BOOL;		// ошибка диапазона    
END_VAR

VAR                  
  VALUES_1: ARRAY[0..15] OF INT; // буфер 1 ступени
  VALUES_2: ARRAY[0..15] OF INT; // буфер 2 ступени
  STEPER_1: WORD; 	// текущий указатель в буфере 1 ступени
  STEPER_2: WORD; 	// текущий указатель в буфере 2 ступени
  TOTAL_1: DWORD ; 	// сумма значений 1 ступени
  TOTAL_2: DWORD ; 	// сумма значений 2 ступени
END_VAR

VAR_TEMP             
  TEMP_VAL: INT;	// временная внутренняя величина
END_VAR

BEGIN

NETWORK
TITLE =  Ограничение и двухступенчатое сглаживание 4..20mA
// Ограничение
  L #INPUT;		// ACCU 1 <- INPUT, входной ток			
  T #TEMP_VAL;		// TEMP_VAR <-ACCU 1, в локальную переменную	
  L 27648;		// ACCU 1 <- константа 20mA, ACCU 2 <- ACCU 1, верхняя граница диапазона
  >I;			// в RLO результат сравнения ACCU 2 > ACCU 1, проверка на превышение 
  = #RANGE;		// RANGE <- RLO	   
  JC A00;		// в ACCU 1 верхняя граница диапазона
  L #TEMP_VAL;		// ACCU 1 <- INPUT
  L 0;			// ACCU 1 <- константа 4mA, нижняя граница диапазона
  <I;			// в RLO результат сравнения ACCU 2 < ACCU 1, проверка на превышение    
  = #RANGE;		// RANGE <- RLO	   
  JCN A01;		// в ACCU 1 нижняя граница диапазона
A00:
  T #TEMP_VAL;		//ограничение входной величины
A01:
// Сглаживание 1 ступени
  L #STEPER_1;		// ACCU 1 <- STEPER_1, загрузка текущего указателя
  L P##VALUES_1;	// ACCU 1 <- @VALUES_1, загрузка указателя на начало массива
  +D;			// ACCU 1 <-  @VALUES_1 + STEPER_1, сдвиг начального адреса на адрес слова
  LAR1;			// AR1 <- ACCU 1, регистр-указатель на нужное слово
  POP;			// ACCU 1 <- ACCU 2,  ACCU 1 <- STEPER_1
  + 16;			// ACCU 1 <- STEPER + 16 (длина слова), на следующий адрес
  AW W#16#00FF;		// ACCU 1 <- ACCU 1 AND 00FF, адрес ограничен одним байтом (16х16)
  T #STEPER_1;		// STEPER <- ACCU 1, сохранить новый адрес
  L #TOTAL_1;		// ACCU 1 <- TOTAL_1, загрузить сумму
  L DIW [AR1,P#0.0];	// ACCU 1 <- VALUES_1[STEPER_1], чтение старого замера
  -D;			// ACCU 1 <- TOTAL_1 - VALUES_1[STEPER_1], вычтем из суммы
  L #TEMP_VAL;		// ACCU 1 <- INPUT(Limiter), новый замер
  T DIW [AR1,P#0.0];	// VALUES_1[STEPER_1] <- ACCU 1, сохранение в буфере
  +D;			// ACCU 1 <- TOTAL_1 + INPUT(Limiter), прибавим к сумме
  T #TOTAL_1;		// TOTAL_1 <- ACCU 1, сохраним новую сумму
  SRD 4;		// ACCU 1 >>>> 4, деление на 16, среднее арифметическое
  T #TEMP_VAL;		// OUTPUT <- ACCU 1, результат в локальную переменную
// Сглаживание 2 ступени
  L #STEPER_2;		// ACCU 1 <- STEPER_2, загрузка текущего указателя
  L P##VALUES_2;	// ACCU 1 <- @VALUES_2, загрузка указателя на начало массива
  +D;			// ACCU 1 <-  @VALUES_2 + STEPER_2, сдвиг начального адреса на адрес слова
  LAR1;			// AR1 <- ACCU 1, регистр-указатель на нужное слово
  POP;			// ACCU 1 <- ACCU 2,  ACCU 1 <- STEPER_2
  + 16;			// ACCU 1 <- STEPER + 16 (длина слова), на следующий адрес
  AW W#16#00FF;		// ACCU 1 <- ACCU 1 AND 00FF, адрес ограничен одним байтом (16х16)
  T #STEPER_2;		// STEPER <- ACCU 1, сохранить новый адрес
  L #TOTAL_2;		// ACCU 1 <- TOTAL_2, загрузить сумму
  L DIW [AR1,P#0.0];	// ACCU 1 <- VALUES_2[STEPER_2], чтение старого замера
  -D;			// ACCU 1 <- TOTAL_2 - VALUES_2[STEPER_2], вычтем из суммы
  L #TEMP_VAL;		// ACCU 1 <- INPUT(Limiter+SMA), новый замер
  T DIW [AR1,P#0.0];	// VALUES_2[STEPER_2] <- ACCU 1, сохранение в буфере
  +D;			// ACCU 1 <- TOTAL_2 + INPUT(Limiter), прибавим к сумме
  T #TOTAL_2;		// TOTAL_2 <- ACCU 1, сохраним новую сумму
  SRD 4;		// ACCU 1 >>>> 4, деление на 16, среднее арифметическое
  T #OUTPUT;		// OUTPUT <- ACCU 1, результат на выход

END_FUNCTION_BLOCK


Для сравнения график исходной функции FB30, постоянная времени фильтра 1,6 сек.



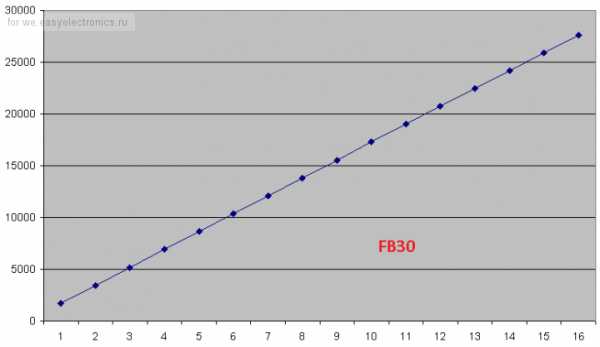
И график «тандемной» функции FB40, постоянная времени фильтра 3,2 сек. График из прямого стал S-образным.


Качественной рускоязычной документации по устройству и программированию Simatic очень много. Перевод как правило произведен фирмой Siemens, и самая полная подборка со свежими исправлениями лежит на официальном сайте. К сожалению для скачивания требуется регистрация.

Приложены:


• Исходник функции FC20.awl в zip;
• Исходник функционального блока FB30.awl в zip;
• Исходник функционального блока FB40.awl в zip;

we.easyelectronics.ru

Сглаживание на выходе

На выходе ЦАП формируется точно такой же ступенчатый аналоговый сигнал, который получался при дискретизации и удерживании. Подобный ступенчатый, или «лестничный» эффект представляет собой искажение, которое необходимо устранить до того, как аналоговый сигнал будет использоваться. Для устранения этого эффекта применяют низкочастотные сглаживающие фильтры, которые иногда путают с «анти-элайсинговыми» фильтрами.



Коммерческие ацп и цап

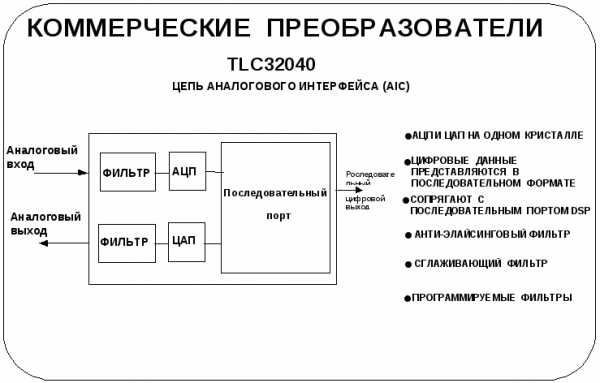
Комплект АЦП и ЦАП размещается на плате DSK. Понимание этой концепции имеет прямое отношение к демонстрациям и общему назначению платыDSK.

На транспаранте представлена упрощенная функциональная схема устройства. Ветвь АЦП на кристалле включает анти-элайсинговый фильтр. После формирования цифровых данных, они поступают на выход в последовательном формате вместе с сигналами управления процессора. Как АЦП, так и ЦАП имеют 14-разрядную разрешающую способность.

Ветвь ЦАП предполагает на входе цифровые данные в последовательном формате. Выходной сигнал ЦАП сглаживают, используя внутрикристальный фильтр с программируемой частотой среза. Это устройство легко сопрягается с последовательным портом устройства ЦОС.



Функциональные блоки платы dsk

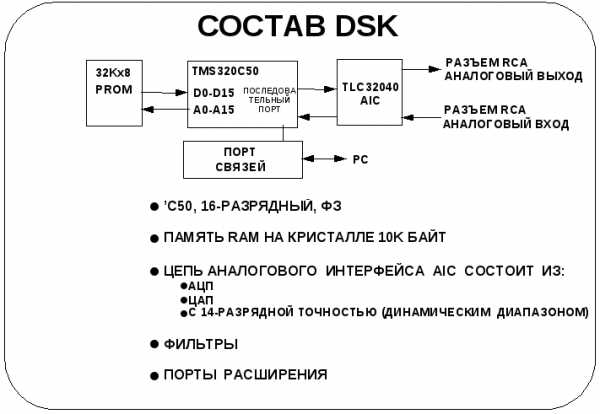
Теперь мы имеем общее представление о ЦПОС и знаем довольно много об АЦП и ЦАП. В большинстве систем ЦОС данные компоненты включены в общий состав.

Поскольку в демонстрациях мы будем использовать плату ’C50DSK, познакомимся с ее составом и функциональным назначением.

Плата DSKвключает:

1. Процессор ’C50.

2. Аналоговую схему интерфейса AIC (AnalogInterfaceCircuit)TLC32040

3. Загрузочную память PROM объемом 32кБ.

Процессор DSP’C50 имеет внутрикристальную памятьRAMобъемом 10К байт, достаточную в большинстве приложений как для хранения программ, так и для хранения данных. Цепь аналогового интерфейсаAICиспользуется для управления всеми аналого-цифровыми преобразованиями. В памятиPROMобъемом 32 кБ, хранится программа начальной загрузки.

Плата DSKимеет дополнительный последовательный порт для подсоединения к РС.

Цепь аналогового интерфейса TLC32040 служит для сопряжения процессора ’C50 с интерфейсом через его последовательный порт. Два стандартных телефонных разъемаRCAобеспечивают аналоговые вход и выход.

Даже если на плате нет доступа к внешней памяти, внутрикристальной памяти RAMобъемом 10К байт процессора ’C50 достаточно для большинства приложений ЦОС. Резидентная программа размещается в памятиPROMобъемом 32к байт, с разрядностью ячеек 8 бит. ПамятьPROMпредназначена исключительно для начальной загрузки платыDSKи недоступна для пользователя в процессе выполнения программы.



Выводы по лекциям

Частота дискретизации должна быть по меньшей мере вдвое выше верхней частоты исходного сигнала для предотвращения элайсинга. Удвоенная верхняя частота обычно называется пределом или частотой Найквиста, при этом часто ссылаются на теорему отсчетов Шеннона.

Поскольку частотный спектр реальных сигналов содержит множество частотных составляющих, для предотвращения элайсинга спектр необходимо ограничить. После фильтрации в сигнале не будет частотных составляющих выше заданной, что позволяет определить безопасную частоту дискретизации.

Типичная цепочка аналого-цифрового преобразования включает: ограничитель спектра (несложный низкочастотный или полосовой фильтр), схему дискретизации и удерживания, квантователь и формирователь цифровых данных. Процедура квантования обязательно вносит ошибки, но их можно уменьшить за счет:

1. увеличения количества уровней квантования,

2. использования неравномерного квантования.

АЦП с последовательным приближением преобразует аналоговые сигналы в цифровые данные посредством сравнения поступающего аналогового сигнала с возможными выходными значениями формирователя цифровых данных. Сигма-дельта АЦП широко используются благодаря их разумной стоимости и надежности цифровой технологии.

ЦАП с умножением напряжения источник действует по принципу получения аналогового сигнала в виде взвешенной суммы, где сумма пропорциональна цифровому входному сигналу.

Плата DSKвключает: процессор ’C50, цепь аналогового интерфейса, последовательный порт для внешних связей и память начальной загрузкиPROM.

studfiles.net

GMSK модуляция

Однако постоянное уплотнение радиочастотного спектра привело к необходимости дополнительного уменьшения уровня боковых лепестков спектра сигнала. Для этого необходимо сгладить фронты импульсов модулирующего цифрового сигнала, поскольку прямоугольный фронт приводит к тому, что фазовая диаграмма MSK (рисунок 1) модуляции имеет точки перелома в моменты времени, соответствующие фронтам импульсов входного цифрового сигнала . Но если мы сгладим фронты входного цифрового сигнала, как это показано на рисунке 1, то получим сглаженный входной сигнал , которому будет соответствовать фазовая диаграмма , которая не имеет точек перелома.


Рисунок 1: Фазовая диаграмма MSK без сглаживания и со сглаживанием фронтов входного цифрового сигнала

В данной статье мы рассмотрим способ сглаживания входного цифрового сигнала при помощи гауссова фильтра и MSK сигналы гауссовой огибающей (Gaussian minimum-shift keying GMSK), получившие широкое распространение в системах сотовой связи стандарта GSM.

Фильтр Гаусса и его характеристики

ФНЧ Гаусса задается импульсной характеристикой вида:

(1)

где — безразмерная величина равная , — полоса фильтра Гаусса по уровню -3дБ, — длительность единичного импульса цифровой информации, передаваемой со скоростью . Например , тогда и при полосе фильтра Гаусса по уровню -3 дБ получаем . Таким образом, параметр показывает во сколько раз полоса фильтра Гаусса отличается от скорости передачи информации , выраженной в единицах измерения частоты.

Отметим, что (1) задает ФНЧ, причем из курса математического анализа известно, что

(2)

тогда обозначив

(3)

получим

(4)

Таким образом, ФНЧ Гаусса на нулевой частоте имеет коэффициент передачи равный 1 для любых . На рисунке 2 представлены импульсные характеристики фильтра Гаусса при и различных параметрах .

На рисунке 3 показана нормированная АЧХ фильтра Гаусса c нормировкой частоты . Таким образом, на рисунке 3 нормированная частота соответствует частоте .

Рисунок 2: Импульсные характеристики фильтра Гаусса при T=1 c и различных BT

Рисунок 3: Нормированная АЧХ фильтра Гаусса при различных параметрах BT

Из рисунка 3 хорошо видно (обозначено пунктирными линиями), что нормированная полоса фильтра Гаусса по уровню -3дБ равна .

Часто на практике требуется использовать цифровой КИХ фильтр Гаусса. Необходимо отметить, что импульсная характеристика фильтра Гаусса (1) является бесконечной, поэтому для использования КИХ фильтра необходимо продискретизировать на ограниченном интервале времени. Мы уже выяснили, что задает полосу фильтра Гаусса относительно длительности импульса цифровой информации. Тогда эффективная ширина импульсной характеристики фильтра Гаусса равна , но , тогда можно записать , т.е. параметр показывает отношение длительности импульса передаваемой цифровой информации и эффективной длительности импульсной характеристики .

Tаким образом для расчета цифрового КИХ фильтра Гаусса необходимо задать границы дискретизации от до , где показывает какое количество импульсов цифровой информации должно учитываться при фильтрации. На практике как правило выбирают , т.е. учитывают 3 импульса до и 3 импульса после. Для расчета КИХ фильтра можно считать коэффициенты КИХ фильтра как , , , — частота дискретизации, тогда , .

Отметим что показывает, сколько отсчетов КИХ фильтра Гаусса приходится на один импульс цифровой информации. Сделаем замечание. Частота дискретизации должна быть больше , поскольку это частота дискретизации, с которой будет производится сглаживание исходного цифрового сигнала, и для сглаживания необходимо чтобы на один импульс приходилось несколько отсчетов. При этом необходимо ввести нормировку коэффициентов КИХ фильтра согласно выражению:

(5)

Формирование GMSK сигналов

Применение Гауссова фильтра при MSK модуляции приводит к GMSK модуляции. Рассмотрим структурную схему GMSK модулятора, показанную на рисунке 4.
Рисунок 4: Структурная схема GMSK модулятора

Входной цифровой сигнал нормируется по амплитуде и получается сигнал с нулевым средним. После подается на сглаживающий фильтр Гаусса , на выходе которого имеем сглаженный сигнал . Этот сглаженный сигнал будет модулирующим сигналом частотного модулятора. Частота девиации при модуляции соответствует частоте девиации MSK . В результате получим на несущей частоте .

Необходимо сделать замечания. Сигнал должен быть нормирован по амплитуде к единице, т.е. . Применение Гауссова фильтра приводит к межсимвольной интерференции тем больше, чем меньше . Например, на рисунках 5-8 приведены осциллограммы сглаженного сигнала при различных значениях и скорости передачи данных .

Из рисунков 5-8 хорошо видно, что уменьшение приводит к расширению эффективной длительности импульсной характеристики фильтра и увеличению межсимвольной интерференции. Для визуальной оценки межсимвольной интерференции удобно использовать глазковые диаграммы представленные на рисунках 9-12.

Из рисунков отчетливо видно, что с уменьшением межсимвольная интерференция усиливается ввиду расширения фильтра Гаусса.

> После сглаживания сигнал подается на FM – модулятор. Необходимо отметить, что сигнал уже является непрерывным и не может быть представлен в виде набора импульсов, поскольку в каждый момент времени в результате межсимвольной интерференции значение зависит не только от текущего импульса цифровой информации, но и от предыдущих импульсов. На вход интегратора (рисунок 4) подается сглаженный сигнал пронормированный к единице .

Частота девиации GMSK берется как и в случае с MSK минимально возможной для разделения сигналов 0 и 1:

.

(6)

После, в соответствии с частотной модуляцией, производится формирования синфазной и квадратурной составляющей комплексной огибающей , и перенос на несущую частоту при помощи универсального квадратурного модулятора.

Комплексная огибающая и спектр GMSK сигнала

На рисунке 13 показаны синфазная и квадратурная составляющие комплексной огибающей MSK сигнала (подробнее смотри здесь). На рисунках 14-17 показаны составляющие комплексной огибающей при GMSK модуляции при различных . Из рисунков 14-17 видно, что при уменьшении составляющие и сглаживаются. На рисунке 18 показан спектр MSK сигнала и GMSK при различных . При построении квадратурных составляющих и спектра скорость передачи , а несущая частота 200 кГц.

Из рисунка 18 можно видеть, что в спектре GMSK при уменьшении уменьшаются уровни боковых лепестков, кроме того значительно возрастает скорость убывания спектра. Так максимальный уровень бокового лепестка GMSK при на 15 дБ меньше чем у MSK сигнала, а скорость убывания линейно зависит от частоты, что обусловлено применением Гауссова фильтра.

Выводы

Таким образом, можно сделать вывод. В данной статье мы рассмотрели свойства фильтра Гаусса и его применение для формирования GMSK модуляции. Показано, что фильтр Гаусса вносит межсимвольную интерференцию и позволяет снизить уровень боковых лепестков спектра, а также значительно увеличивает скорость убывания спектра GMSK сигнала по сравнению с MSK сигналами. На практике GMSK модуляция нашла применение в сотовой связи формата GSM при , ввиду наиболее эффективного использования радиочастотного ресурса. Дальнейшее уменьшение параметра приводит к существенному усложнению аппаратуры и сильно увеличивает вероятность ошибочного приема символа из-за недопустимо высокой межсимвольной интерференции.

ru.dsplib.org

Об одном забавном подходе к фильтрации унимодальных сигналов

В этой статье наши инженеры хотели бы поделиться с Хабром достаточно интересным инструментом, который можно эффективно применять для фильтрации зашумленных сигналов, пользуясь априорным знанием об унимодальности сигнала.

Задача оффлайновой фильтрации сигналов в случае, когда ожидаемая форма сигнала известна с точностью до нескольких неизвестных параметров, сводится к задаче аппроксимации. Например, если известно, что сигнал линейно растет на рассматриваемом промежутке, задача сведётся к линейной регрессии, а если можно предположить, что шум — нормален, то правильным методом будет МНК. Но однажды мы столкнулись с задачей оценки формы профиля рентгеновского микрозонда (пучка), про которую априори было достоверно известно только одно: профиль унимодален, а именно имеет ровно один максимум. Оказывается, и в этом случае можно наилучшим (в смысле, например, L2 метрики) образом приблизить экспериментальный сигнал функцией, принадлежащей известному множеству (множеству унимодальных функций). Причём — с приемлемой ассимптотикой вычислительной сложности.

===> ===>

Итак, речь пойдёт о задаче аппроксимации некоторого зашумлённого сигнала как функции дискретного аргумента , причем известно, что исходный сигнал — унимодальный. В рассматриваемом случае дополнительно известно, что на краях сигнал ассимптотически приближается к нулю. Следует отметить, что рассматриваемый ниже метод сам по себе не требует такого допущения.

Вначале, для простоты изложения, имеет смысл рассмотреть ту же задачу для монотонной функции. Описание приведено для монотонно нестрого возрастающей функции, хотя, разумеется, для монотонно убывающей можно проделать всё то же самое.

Если предположить, что шум нормально распределен, то задача сведётся к минимизации квадратичного функционала в присутствии неравенств вида . Это — задача квадратичного программирования, и для нее на просторах интернета можно найти некоторое количество готовых решателей. Но, во-первых, задача квадратичного программирования в общем случае обсчитывается довольно медленно, а во-вторых, задача аппроксимации унимодального сигнала не выписывается в подобном виде, если положение экстремума не известно заранее.

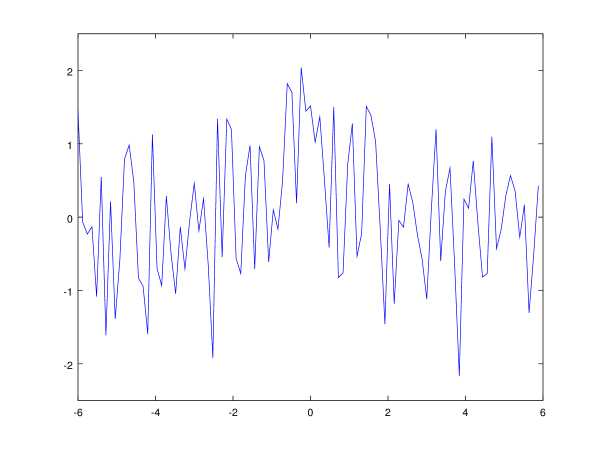
Существует альтернативное решение, не обладающее указанными недостатками, но при его использовании шкалу сигнала придётся считать дискретной. Тут стоит отметить, что задача не интересна в случае слабого шума, поскольку обычная линейная фильтрация, скорее всего, снимет все практические проблемы. Что же такое интересный, сильный шум? На рис. 1 можно увидеть модельный сигнал до и после такого зашумления. Шум здесь задан нормальным распределением . В подобных условиях дискретизация аппроксимирующего сигнала не выглядит существенной потерей. Кроме того, как будет видно далее, при увеличении числа отсчетов сложность вычислений будет возрастать линейно.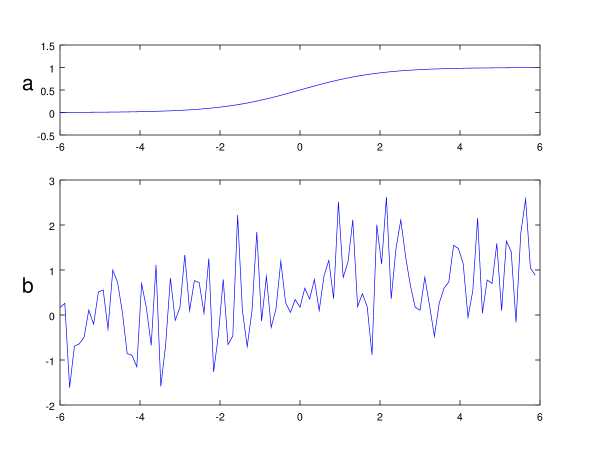

Рис. 1: a) Модельный монотонный сигнал до налолжения шума. b) Модельный монотонный сигнал после наложения шума.

Оказывается, в дискретном приближении фильтрация нормально зашумленного монотонного сигнала сводится к динамическому программированию с двумя параметрами, причём, пользуясь этим решением, удаётся построить вычислительную схему той же сложности и для унимодального случая.

О том, что такое динамическое программирование, можно почитать здесь, а как и к каким задачам его применяют — здесь.

Фильтрация монотонного сигнала методом динамического программирования


В рассматриваемой задаче таблица динамического программирования — двумерная, её столбцам i соответствуют возрастающие слева направо значения дискретного аргумента экспериментальных точек, а строкам j — возрастающие снизу вверх возможные значения аппроксимирующей функции . Минимизируемый функционал — сумма квадратов отклонений от вдоль путей с допустимыми переходами. Очевидно, что допустимыми будут переходы на 1 вправо с одновременным неотрицательным смещением вверх.

Внешний цикл ведётся по координате i слева направо. Для каждого значения выполняется внутренний цикл по координате j снизу вверх. Минимальное значение функционала определяется по формуле


причём за пределами таблицы функционал считается равным нулю.

При этом, чтобы не пересчитывать каждый раз минимум на меньших значениях j, его полезно сохранять в процессе заполнения вместе со значением функционала, а поскольку в конце требуется восстановить путь, сохранять удобнее значение m, на котором этот минимум был достигнут:


Тогда вычисление самого функционала можно выполнять за O(1) для каждой ячейки:
После завершения прямого прохода остаётся получить аппроксимацию в явном виде. Для этого ищется минимум среди значений функционала для крайнего правого столбца (столбца с наибольшей координатой i), а затем выполняется обратный проход по i, с восстановлением индекса значения отфильтрованного сигнала j* в каждом столбце:
Окончательные значения определяются как
На рис. 2 показан пример результата описанного алгоритма для монотонного сигнала.

Рис. 2: Фильтрация монотонно возрастающего сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.

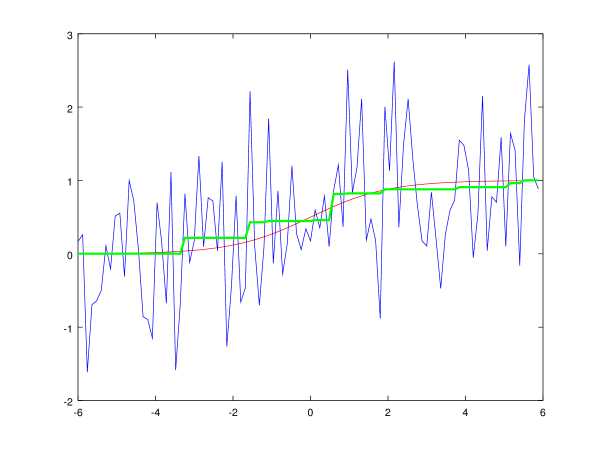
На этом рассмотрение вспомогательного монотонного случая закончено.

Унимодальный сигнал


Используя полученный результат, можно решить задачу об унимодальном сигнале, заполнив 2 таблицы ДП: одна заполняется как для монотонной функции, вторая — таким же образом, но в обратную сторону. В результате вычисляется 2 функционала: и , а также значения и для восстановления путей по таблицам. После этого среди всех значений i и j ищется такоая пара , для которой сумма функционалов минимальна — это будут индексы максимума аппроксимированной функции. Значения функции с каждой стороны от него восстанавливаются по соответствующей таблице.


На рисунках 3 и 4 показан пример исходного унимодального сигнала и результата его обработки предложенным алгоритмом.

Рис. 3: Зашумлённый унимодальный сигнал.

Рис. 4: Фильтрация унимодального сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.

Ограничение на производную


В случае, если известно, что сигнал не может меняться быстрее некоторой фиксированной скорости (что вполне вероятно), точность регрессии можно улучшить, введя это ограничение в алгоритм в явном виде. Для этого достаточно вычислить максимально возможное изменение индекса значения сигнала для каждого i и запретить переходы в таблице ДП с изменением j более, чем на эту величину:

Правда, чтобы не проиграть в трудоёмкости, нужно иметь возможность получать минимальное значение функционала на отрезке [j — dj, j] за константное время.
Это можно сделать с помощью алгоритма Ван Херка — Гила — Вермана, описанного, например, здесь.

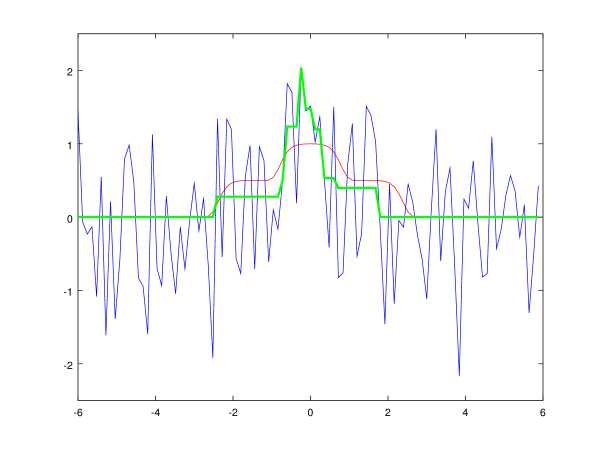
Результат применения алгоритма с ограничением на производную показан на рис. 5.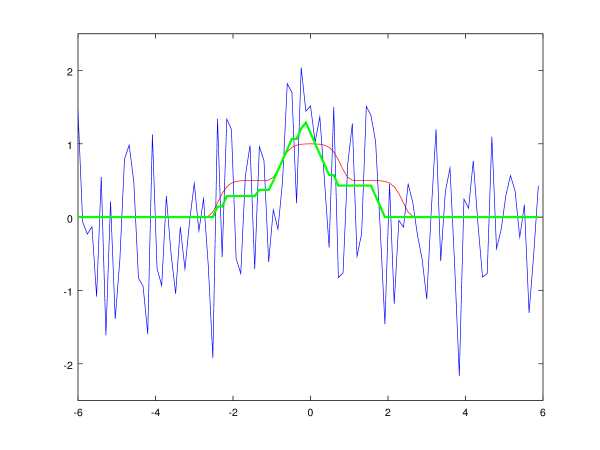

Рис. 5: Фильтрация унимодального сигнала динамическим программированием с ограничением на скорость изменения сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.

Разоблачение чёрной магии


Пытливый читатель может заподозрить, что таких же или лучших результатов можно достигнуть более простыми способами. Конечно, при определённых параметрах сигнала и шума описанная техника будет излишней. Кроме того, короче та дорога, которую знаешь. Поэтому на каждый хитрый случай у специалиста наверняка найдётся любимый метод, который именно в его руках даст приемлемый результат.

Чтобы рассеять ощущение возможного мошенничества, на рис. 6 и 7 приведены примеры обработки сигнала гауссовским сглаживанием и медианной фильтрацией с зашкаливанием в нуле. Параметры фильтров подбирались с целью получения оптимального результата, но без фанатизма.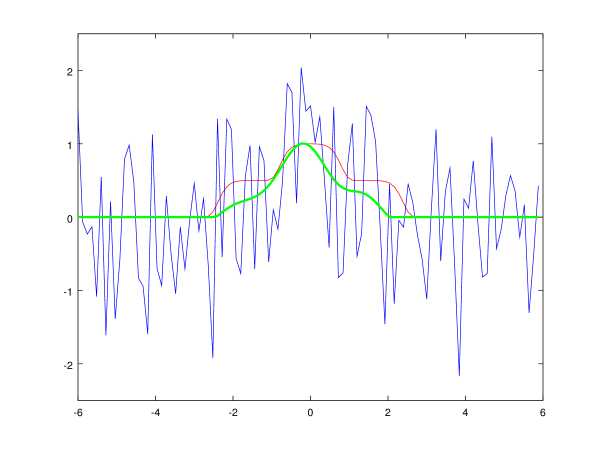

Рис. 6: Фильтрация унимодального сигнала гауссовским сглаживанием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.

Рис. 7: Медианная фильтрация унимодального сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.

Как видно, на достаточно произвольных данных метод динамического программирования дает результат получше, чем простейшие общеизвестные фильтры. При этом сравнивать их на модельных примерах подробно — абсолютно бессмысленно. Изложенный выше метод ценен ровно тем, что является примером “костюма, сшитого по мерке”: формализованная постановка задачи была положена в саму основу метода. В рассматриваемом случае это было условие унимодальности. Аналогично, линейные методы “по мерке” сигналам, частотно разделимым с шумом. Еще один инструмент в наборе — что может быть лучше для инженера?

habr.com

Сглаживание сигналов и изображений с сохранением границ методом динамического программирования Текст научной статьи по специальности «Автоматика. Вычислительная техника»

УДК 621.317.35

А.В. Копылов, А.С. Карцева (Тула, ТулГУ)

СГЛАЖИВАНИЕ СИГНАЛОВ И ИЗОБРАЖЕНИЙ С СОХРАНЕНИЕМ ГРАНИЦ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рассматриваются два алгоритма динамическою программирования в задаче сглаживания сигналов и изображений, позволяющих учитывать различные априорные предположения о гладкости результата обработки, включая предположения о наличии существенных неоднооодностее, разуывов или скачков, и имеющих линейную вычислительную сложность относительно числа целевых переменных.

Задача сглаживания с сохранением границ является типичной в практике обработки сигналов и изображений. Она постоянно возникает, когда есть основания предполагать наличие существенных неоднородностей, разрывов или скачков в искомом, сглаженном изображении, которые замаскированы шумом во вторичных данных, доступных непосредственной обработке.

Далее рассматриваются два подо да к сохранению границ в задаче обобщенного сглаживания. Первый основан на пошаговом нахождении граничных точек при помощи процедры динамического программирования «вперед и навстречу» [1] и учете ж при даьнейшем формировании критерия оптимизации, а второй — на использовании вместо квадратичной функции связи, имеющей смысл штрафа на негладкость искомого сигнаа, функции, имеющей вид модуля разности соседних элементов данных, что, как покаано в работе, также дает эффект сохранения границ.

Основная идея сглаживания данных древовидной структуры с сохранением границ. Будем рассматривать изображение как действительнозначную функцию У = (у^, 1 е Т), которая принимает значения из некоторого подходящего множества у е У и определена на дискретном множестве Т = (1 = (11,12): tl = 1,…,N1,?2 =1,…,N2}.

В рамках оптимизационного подхода к проблеме сглаживания алгоритм анаиза данных строим как агорит минимизации подходящей целевой функции J(х|у), определенной на множестве всех возможных вариантов вторичного массива данных X = (х^1 еТ) и ирающей роль

штрафа на несоответствие между каждой возможной версией результата и обрабатываемого массива данных У = (у 11 е Т).

Каждый элемент сигнаа или изображения естественным обраом связан с некоторым количеством своих соседей. Отношение соседства удобно выражать в виде неориентированного графа О, который определяется множеством пар соседних друг с другом элементов О с Т х Т. Для

сигналов естественным представлением графа соседства переменных О является цепь, представляющая собой вырожденный случай дерева. Простейшим графом соседства для изображений обычно является прямоугольна решетка (рис. 1,а), но для создания не итерационной процедуры обработки наиболее удобным будет аппроксимировать ее последовательностью деревьев (рис. 1,б), каждый раз оставляя вертикальные связи лишь в одном из столбцов.

1 —————Ц —————а;

Рис. 1. Граф соседства на множестве элементов изображения: а — прямоугольная решетка; б — дерево

С учетом отношений соседства подобного вида целева функция практически всегда может быть выбрана в так называемой сепарабельной форме как сумма двух типов функций, называемых узловыми функциями и функциями связи:

3 (Х|¥ )= (Хг|Уг)+ ХУг’, г «(хг ■>х 1»)- (1)

геТ (1″о

Узловые функции (х | У г) выбираются в зависимости от конкретной решаемой задачи таким обраом, что кажда из них принимает тем большее значение, чем более очевидно расхождение между гипотезой о том, что Хг является искомым локаьным значением, и соответствующей

окрестностью Уг массива данных. Кажда функция связи у гХг»Хг» налагает штраф на раличие значений пары соседних переменных, то есть на негладкость результата на соответствующем ребре (г», г») графа соседства.

При использовании аппроксимации графа соседства в виде решетки последовательностью деревьев минимизация сепарабельной целевой функции осуществляется посредством эффективной глобаьной процедуры, подобной процедре динамического программирования [1]. Оптимизационна процедра для целевой функции с древовидной сепааабельностью основана на том факте, что удаление любого ребра (г»» е О рабивает дерево на два не связанных друг с другом поддерева О!»» и О » (рис. 2), оп-

ределенных на соответствующих непересекающихся множествах вершин Т»^ и Т»» , так что Т = Т^’ иГ1’1». Если У»(Х»‘1») и У^»(Х»») — частичные целевые функции соответствующих частичных векторов переменных, исходна целевая функция может быть представлена в виде суммы

У(Х) =у» ‘№г)+УГ1″(Х» , Ъ»)+Г»ч» (X? г)- (2)

V V»

J’t fit Т» rpff Н Г'»

1’Г iriY -Чг 1tY ( Vt* ‘ЧГ

Рис. 2. Два поддерева, соединенных ребром (t ‘,tf)

В дополнение введем обозначения:

У»‘1′(х1»)= т*п У1’г(ХГ1’X ‘~»г'(х1″) = т*п У»V(Х»г)- (3)

XX^ \»

8^1» 8^1″

Две функции (3), определенные в узах, соединенных ребром (О») , имеют тот же смысл, что и функции Беллмана в классической процедуре динамического программирования, поэтому назовем их левосторонней и правосторонней функциями Беллмана для ребра (1,1″) или возможно, верхней и нижней функциями в зависимости от ориентации соответствующего ребра.

Основным свойством функции Беллмана является тот факт, что

тт У(X) = тт {У’ ‘» (х’) + у 1 ^» (х’», X'») + У’у’ (X’» )} =

X X’» , X’»

= тт(тт[у» ‘1 » (X’») + у^1″(Х’»,X’»)]+ »(х 1″ )}. (4)

х1″ х1′

В задачах обработки изображений граф смежности переменных, соответствующий целевой функции (рис. 1,а)

ч N N2 , V N N2 , V

У(Х|У)= X Е пх^21^2)+ Е Е у'(2-1,х^2)

Ь=Щ =1 Ч =212 =2 (5)

N1 N2 ( ) ()

+ Е Е у»( — 2,х^21

Ч=212=2

не является деревом и метод сглаживания с сохранением границ, рассмотренный в предыдущем разделе, не может быть непосредственно применен к изображениям.

Превратить граф в виде решетки в дерево можно удалением некоторых ребер, например вертикальных, за исключением одного столбца, как показано на рис. 1,б. Но сокращенный граф соседства не позволит обеспечить гладкость искомого массива данных во всех направлениях для каждого элемента растра. Эта возможность сохранится лишь для узлов соответствующего вертикального столбца. В качестве компромиссного решения подход, рассмотренный в работе [2], предлагает приять отимшьные значения переменных в одном столбце с сохраненными вертикальными связями, например ?1, в качестве финальных оценок элементов скрытого массива данных для этого столбца. Такая процедура повторяется для каждого из возможных деревьев с 11=1,…,N1 с теми же горизонтальными ветвями. В данной работе используется именно этот способ обработки изображения с тем отличием, что для каждого дерева используется процедура сглаживания с сохранением границ, описанная ранее.

Очевидно, что чем более безразличной задана функция связи, т.е. чем меньше она отличается от нуля с ростом несоответствия (X’» — X’»),

тем меньше будет минимальное значение целевой функции тт У(Х). Но

Х

степень подобной зависимости должна быть различной для различных пар соседних переменных, и чем она больше, тем более вероятно предположение о том, что рассматриваемая пара содержит еще не найденный скрытый скачок в массиве данных.

Итерационный метод сглаживания сигналов и изображений, основанный на понятии напряженности. Пусть функция уу’ » (X’»,X’») является основной, в достаточной мере жесткой функцией связи, обеспечивающей требуемую степень сглаживания на ребре (1 ‘,1 «) графа соседства переменных, для которого скачок еще не зафиксирован, а функция *

УУ (X'»,X’’) — более мягкая функция связи, допускающая наличие скачков. Если отношение

тт {У»‘» (X'») + у у'» (X'», X’*) + Ууу (X у )}

Ч1, x 1″

г1 1″ =——————————————————-7-*-7- (6)

тт {Ууу (X'») + У у'» (X'», xi•) + Ууу (X у )}

xt’,x1″

превышает некоторый заданный порог г 1 ‘» > к, то будем считать, что для данной пары соседних переменных возможен скачок. Пусть ^ » принимает значение (6) при превышении порога к и ноль — в противном случае. Будем называть неотрицательную переменную г^у напряженностью на ребре (1 «,1»). Последовательно вычислим напряженность гуу для всех ребер графа соседства. Ребра (1 «Д»), где напряженность достегает своего абсолютного максимума одновременно на всех ветвях двух соседних подде-

ревьев внутри интервала А, содержат новые найденные скачки. Это означает, что функция связи у у’ » (xt», X'») ребра (1 «,1» ) должна быть заменена

*

на более безразличную у у » (xt», xt»). Процедура начинает свою работу при исходных основных функциях связи в предположении, что в исходном массиве скачки отсутствуют. Затем процедура запускается вновь с другим набором функций связи, пока не останется ребер с положительным значением напряженности. Данный алгоритм может обнаружить скачки, расположенные ближе друг к другу, чем размер интервала А, но делает это последовательно на разных стадиях обработки.

В качестве примера рассмотрим задачу обычного сглаживания изображений с сохранением границ. В этом случае узловые функции и функции связи приняты квадратичными и имеют достаточно постой вид:

v{xht2 1^,,,2 2 —V2’

У¥2 (1С<1,<2“ЬЩ2)= и<1>2 (— ~:(Н12 )2 , (7)

к а 2

у,2 -1,,2 ,Xt1t2 ) = М¥2 “М2 “ -С,1,2 ) .

Локальной оценкой сглаженного значения интенсивности изображения xOt является значение яркости соответствующего элемента изображения. Таким образом, элементарный фрагмент изображения состоит из единственного элемента У,1,2 = у,,2 . Коэффициенты вертикальных и горизонтальных узловых функций и»1,2 и и»‘,2 принимают положительные

значения для ребер, на которые распространяются ограничения гладкости, и нулевые значения для ребер, где зафиксирована возможность резких изменений интенсивности.

Пример обработки изображения с использованием описанной процедуры сглаживания с сохранением границ приведен на рис. 3. Он получен за гать итераций с использованием интервала А = 2 .

Как видно на рис. 3,б, алгоритм смог обнаружить резкие перепады яркости, расположенные очень близко друг к другу в отличие, например, от процедуры динамического программирования с квадратичными функциями связи, результат работы которой показан на рис. 3 ,в.

Неитерационный алгоритм сглаживания сигналов

с использованием модуля разности отсчетов сигнала в качестве функции штрафа на негладкость. Предложенный далее метод сглаживания использует в качестве функции связи в рассмотренной выше процедуре динамического программирования модуль разности локальных оценок синалав двух соседних точках.

1М91?аМШт11! , 1л(е1Рсп

а б в

Рис. 3. Результаты сглаживания тестового изображения: а — исходное изображение; б — слаженное процедурой с сохранением границ; в — слаженное процедурой динамического программирования с использованием квадратичных функций связи с сопоставимой

степенью сглаживания

Пусть функция связи

у,,,-(X,,X, — ) = u|xt -X,_1|, и >0. (8)

Предположим, что функция Беллмана на предыдущем шаге У, — (X,_) выпукла и дифференцируема всюду в области определения. Тогда ее производная •//_(X,_)=———«/,_(X,-) монотонно возрастает.

dxt—

Можно доказать, что функция Беллмана и обратное рекуррентное

и / и

соотношение на каждом шаге завися от параметров л( — и xt —, которые

определяются как решение уравнений У,—1 (/,1-) = — и У-/^) = исоответственно. Обратное рекуррентное соотношение /_-(X,) в таком случае

и

полностью определяется своими параметрами X, — и X,- и является кусочно-линейной функцией [3].

Предложенный метод можно использовать также для сглаживания изображений с учетом сделанных предположений о древовидной структуре графа соседства. Пример сглаживания изображений приведен на рис. 4.

Для обработки тестового изображения на рис. 4, а узловые функции выбраны квадратичными, а функции связи представляют собой модуль разности значений искомого сигнал в соседних точках:

Л I ,12 — ^

Уу,2 (^,1,2 -1, Xtl2)= И ¥2 X ,1,, 2 — — -С,1,2 . (9)

г

It

ч

V

а б

Рис. 4. Результаты сглаживания изображения: а — исходное

изображение; б — слаженное процедурой х функцией связи

в виде модуля разности

Как показывают исследования, использование функции модул позволяет получать изображения с необходимой степенью сглаживания, и в то же время локальные особенности исходного массива данных в виде резких перепадов яркости изображения четко отслеживаются и сохраняются процедурой обработки.

Библиографический список

1. Muchnik I. Bellman Functions of Trees for Segmentation, Generalized Smoothing, Matching and Multi-Alignment in Massive Data Sets /1. Muchnik, V. Mottl // DIMACS Technical Report 98-15, Rutgers University, USA. -1998.-P. 63.

2. Optimization techniques on pixel neighborhood graphs for image processing / V. Mottl [et al.] // Graph-Based Representations in Pattern Recognition. Computing, Supplement 12. Springer-Verlag/Wien. — 1998. — P. 135-145.

3. Копылов А.В. Критерии и алгоритмы оценивания нестационарной регрессии в анаизе временных радов / А.В. Копылов, О.В. Красотки-на, В.В. Моттль // Математические методы распознавания образов: 12-я Всероссийска конференция: Сборник докладов.- М.: МАКС Пресс, 2005. -С. 140-144.

Получено 23.04.08

cyberleninka.ru

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт